WikiDer > Диаграммы углового момента (квантовая механика)

Часть серии на
Квантовая механика
${ displaystyle i hbar { frac { partial} { partial t}} | psi (t) rangle = { hat {H}} | psi (t) rangle}$ Уравнение Шредингера
Вступление Глоссарий История Учебники
Фон Классическая механика Старая квантовая теория Обозначение Бра – Кет Гамильтониан Вмешательство
Основы Согласованность Декогеренция Комплементарность Уровень энергии Запутанность Гамильтониан Принцип неопределенности Основное состояние Вмешательство Измерение Нелокальность Наблюдаемый Оператор Квантовая Квантовая флуктуация Квантовое число Квантовый шум Квантовая область Квантовое состояние Квантовая система Квантовая телепортация Кубит Вращение Суперпозиция Симметрия (Спонтанное) нарушение симметрии Состояние вакуума Распространение волн Волновая функция Коллапс волновой функции Дуальность волна-частица Волна материи
Последствия Эффект Зеемана Эффект Старка Эффект Ааронова – Бома Квантование Ландау Квантовый эффект Холла Квантовый эффект Зенона Квантовое туннелирование Фотоэлектрический эффект Эффект Казимира
Эксперименты Неравенство Белла Дэвиссон-Гермер Двойная щель Элицур – Вайдман Франк-Герц Неравенство Леггетта – Гарга Мах – Цендер Поппер Квантовый ластик (отложенный выбор) Кот Шредингера Штерн-Герлах Отсроченный выбор Уиллера
Составы Обзор Гейзенберг Взаимодействие Матрица Фазовое пространство Шредингер Суммирование по историям (интеграл по путям)
Уравнения Дирак Хеллманн-Фейнман Кляйн – Гордон Липпманн-Швингер Паули Ридберг Шредингер
Интерпретации Обзор Байесовский Последовательные истории Копенгаген де Бройль-Бом Ансамбль Скрытая переменная Многомиры Объективный коллапс Квантовая логика Реляционный Стохастик Транзакционный
Дополнительные темы Квантовый отжиг Квантовый хаос Квантовые вычисления Квантовая геометрия Матрица плотности Квантовая теория поля Дробная квантовая механика Квантовая гравитация Квантовая информатика Квантовое машинное обучение Теория возмущений (квантовая механика) Релятивистская квантовая механика Теория рассеяния Самопроизвольное параметрическое преобразование с понижением частоты Квантовая статистическая механика
Ученые Ааронов Колокол Блэкетт Блох Бом Бор Родившийся Bose де Бройль Кэндлин Комптон Дирак Дэвиссон Дебай Эренфест Эйнштейн Эверетт Фок Ферми Фейнман Глаубер Gutzwiller Гейзенберг Гильберта Иордания Крамерс Паули ягненок Ландо Лауэ Мозли Милликен Оннес Планк Раби Раман Ридберг Шредингер Зоммерфельд фон Нейман Weyl Вена Вигнер Zeeman Цайлингер Goudsmit Уленбек Ян
Категории ► Квантовая механика
v т е

В квантовая механика и его приложения к квантовые системы многих частиц, особенно квантовая химия, диаграммы углового момента, а точнее с математической точки зрения графики углового момента, представляют собой схематический метод представления угловой момент квантовые состояния квантовой системы, позволяющей производить расчеты символически. Более конкретно, стрелки кодируют состояния углового момента в обозначение бюстгальтера и включать абстрактный характер государства, например тензорные произведения и правила преобразования.

Обозначения параллельны идее Графическое обозначение Пенроуза и Диаграммы Фейнмана. Диаграммы состоят из стрелок и вершин с квантовые числа как ярлыки, отсюда и альтернативный термин "графики". Смысл каждой стрелки связан с Эрмитово спряжение, что примерно соответствует разворот времени состояний углового момента (см. Уравнение Шредингера). Обозначения на диаграммах - это довольно большая тема, обладающая целым рядом специальных функций - эта статья знакомит с самыми основами.

Они были разработаны в первую очередь Адольфас Джусис (иногда переводится как Юцис) в ХХ веке.

Эквивалентность нотации Дирака и диаграмм Жусиса

Состояния углового момента

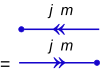
В квантовое состояние вектор одиночной частицы с полным квантовое число углового момента j и всего магнитное квантовое число м = j, j − 1, ..., −j + 1, −j, обозначается как кет |j, м⟩. В виде диаграммы это Одиннаправленная стрелка.

Симметрично соответствующий бюстгальтер ⟨j, м|. В виде диаграммы это двойнойнаправленная стрелка, указывающая в направлении, противоположном кету.

В каждом случае;

• квантовые числа j, м часто помечаются рядом со стрелками для обозначения определенного состояния углового момента,
• наконечники стрел почти всегда располагаются посередине линии, а не на конце,
• знаки равенства «=» помещаются между эквивалентными диаграммами, как и для нескольких равных друг другу алгебраических выражений.

Самые простые схемы для кетов и бюстгальтеров:

Кет |j, м⟩

Бюстгальтер ⟨j, м|

Стрелки направлены к вершинам или от вершин, состояние изменяется в соответствии с:

• а стандартное представление обозначается ориентированной линией, выходящей из вершины,
• а противоречивое представление изображается как линия, входящая в вершину.

Как правило, стрелки следуют друг за другом в одном и том же смысле. В контрастном представлении разворот времени оператор, обозначаемый здесь Т, используется. Он унитарен, что означает Эрмитово сопряжение Т^† равно обратному оператору Т⁻¹, то есть Т^† = Т⁻¹. Его действие на оператор позиции оставляет его неизменным:

${ Displaystyle T { шляпа { mathbf {x}}} T ^ { dagger} = { шляпа { mathbf {x}}}}$

но линейный оператор импульса становится отрицательным:

${ Displaystyle T { шляпа { mathbf {p}}} T ^ { dagger} = - { hat { mathbf {p}}}}$

и вращение оператор становится отрицательным:

${ Displaystyle T { шляпа { mathbf {S}}} T ^ { dagger} = - { hat { mathbf {S}}}}$

Поскольку орбитальный оператор углового момента является L = Икс × п, это также должно стать отрицательным:

${ Displaystyle T { шляпа { mathbf {L}}} T ^ { dagger} = - { шляпа { mathbf {L}}}}$

и, следовательно, оператор полного углового момента J = L + S становится отрицательным:

${ Displaystyle T { шляпа { mathbf {J}}} T ^ { dagger} = - { hat { mathbf {J}}}}$

Воздействие на собственное состояние углового момента |j, м⟩, можно показать, что:^[1]

${ Displaystyle Т влево | J, м вправо rangle эквив влево | Т (J, м) вправо rangle = {(- 1)} ^ {JM} влево | J, -m вправо rangle}$

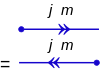
Диаграммы с обращением времени для кетов и бюстгальтеров:

Время перевернутое кет |j, м⟩.

Бюстгальтер с переворотом ⟨j, м|.

Важно правильно расположить вершину, так как операторы прямого и обратного времени могут смешаться.

Внутренний продукт

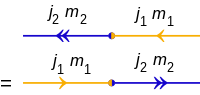
Внутренний продукт двух состояний |j₁, м₁⟩ и |j₂, м₂⟩ является:

${ displaystyle langle j_ {2}, m_ {2} | j_ {1}, m_ {1} rangle = delta _ {j_ {1} j_ {2}} delta _ {m_ {1} m_ { 2}}}$

и диаграммы:

Внутренний продукт из |j₁, м₁⟩ и |j₂, м₂⟩, то есть ⟨j₂, м₂|j₁, м₁⟩.

Эквивалент обратного времени.

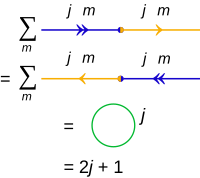
Для суммирования по внутреннему произведению, также известного в этом контексте как сокращение (см. тензорное сжатие):

${ Displaystyle сумма _ {м} langle j, m | j, m rangle = 2j + 1}$

принято обозначать результат в виде замкнутого круга, помеченного только j, нет м:

Сокращение внутреннего продукта.

Внешние продукты

Внешний продукт двух состояний |j₁, м₁⟩ и |j₂, м₂⟩ это оператор:

${ displaystyle left | j_ {2}, m_ {2} right rangle left langle j_ {1}, m_ {1} right |}$

и диаграммы:

Внешний продукт из |j₁, м₁⟩ и |j₂, м₂⟩, то есть |j₂, м₂⟩⟨j₁, м₁|.

Эквивалент обратного времени.

Для суммирования по внешнему произведению, также известного в этом контексте как сокращение (см. тензорное сжатие):

${ displaystyle { begin {align} sum _ {m} | j, m rangle langle j, m | & = sum _ {m} | j, -m rangle langle j, -m | & = sum _ {m} {(- 1)} ^ {2 (jm)} | j, -m rangle langle j, -m | & = sum _ {m} {(- 1 )} ^ {jm} | j, -m rangle langle j, -m | {(- 1)} ^ {jm} & = sum _ {m} T | j, m rangle langle j , m | T ^ { dagger} end {align}}}$

где результат для Т|j, м⟩ был использован, и тот факт, что м принимает набор значений, приведенных выше. Нет никакой разницы между состояниями прямого и обратного времени для сжатия внешнего продукта, поэтому здесь они имеют одну и ту же диаграмму, представленную в виде одной линии без направления, снова обозначенной j только и не м:

Сужение внешнего продукта.

Тензорные продукты

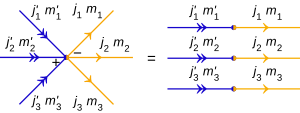
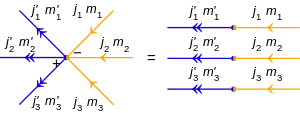
Тензорное произведение ⊗ п состояния |j₁, м₁⟩, |j₂, м₂⟩, ... |j_п, м_п⟩ написано

${ displaystyle { begin {align} left | j_ {1}, m_ {1}, j_ {2}, m_ {2}, ... j_ {n}, m_ {n} right rangle & Equiv left | j_ {1}, m_ {1} right rangle otimes left | j_ {2}, m_ {2} right rangle otimes cdots otimes left | j_ {n}, m_ {n} right rangle & Equiv left | j_ {1}, m_ {1} right rangle left | j_ {2}, m_ {2} right rangle cdots left | j_ {n}, m_ {n} right rangle end {align}}}$

а в форме диаграммы каждое отдельное состояние покидает или входит в общую вершину, создавая «веер» стрелок - п линии, прикрепленные к одной вершине.

Вершины в тензорных произведениях имеют знаки (иногда называемые "знаками узлов"), чтобы указать порядок состояний, умноженных на тензор:

• а минус знак (−) указывает, что заказ по часовой стрелке, ${ displaystyle circlearrowright}$, и
• а плюс знак (+) за против часовой стрелки, ${ displaystyle circlearrowleft}$.

Знаки, конечно, не требуются только для одного состояния, схематично - одна стрелка в вершине. Иногда включаются изогнутые стрелки со знаками, чтобы явно показать смысл умножения тензора, но обычно отображается только знак с опущенными стрелками.

Тензорное произведение из |j₁, м₁⟩, |j₂, м₂⟩, |j₃, м₃⟩, то есть |j₁, м₁⟩|j₂, м₂⟩|j₃, м₃⟩ = |j₁, м₁, j₂, м₂, j₃, м₃⟩. Аналогично для более трех угловых моментов.

Эквивалент обратного времени.

Для внутреннего произведения двух состояний тензорного произведения:

${ displaystyle { begin {align} & left langle j '_ {n}, m' _ {n}, ..., j '_ {2}, m' _ {2}, j '_ { 1}, m '_ {1} | j_ {1}, m_ {1}, j_ {2}, m_ {2}, ... j_ {n}, m_ {n} right rangle = & langle j '_ {n}, m' _ {n} | ... langle j '_ {2}, m' _ {2} | langle j '_ {1}, m' _ {1} || j_ {1}, m_ {1} rangle | j_ {2}, m_ {2} rangle ... | j_ {n}, m_ {n} rangle = & prod _ {k = 1} ^ {n} left langle j '_ {k}, m' _ {k} | j_ {k}, m_ {k} right rangle end {выровнено}}}$

Существуют п множество внутренних стрелок продукта:

Внутренний продукт из |j′₁, м′₁, j′₂, м′₂, j′₃, м′₃⟩ и |j₁, м₁, j₂, м₂, j₃, м₃⟩, то есть ⟨j′₃, м′₃, j′₂, м′₂, j′₁, м′₁|j₁, м₁, j₂, м₂, j₃, м₃⟩. Аналогично для более чем трех пар угловых моментов.

Эквивалент обратного времени.

Примеры и приложения

• Диаграммы хорошо подходят для Коэффициенты Клебша – Гордана.
• Расчеты с реальными квантовыми системами, такими как многоэлектронные атомы и молекулярный системы.

Схема для 6-j символ, ${ displaystyle { begin {Bmatrix} j_ {1} & j_ {2} & j_ {3} j_ {4} & j_ {5} & j_ {6} end {Bmatrix}}}$.

Схема для 9-j символ, ${ displaystyle { begin {Bmatrix} j_ {1} & j_ {2} & j_ {3} j_ {4} & j_ {5} & j_ {6} j_ {7} & j_ {8} & j_ {9} конец {Bmatrix}}}$.

Смотрите также

• Векторная модель атома
• Оператор лестницы
• Пространство фока
• Диаграммы Фейнмана

Рекомендации

• Юцис, Адольфас П .; Левинсон, И. Б .; Ванагас, В. В. (1962). Математический аппарат теории углового момента.. Перевод А. Сена; Р. Н. Сен. Израильская программа научных переводов.
• Вормер и Палдус (2006)^[1] предоставляет подробное руководство по диаграммам углового момента.
• И. Линдгрен; Дж. Моррисон (1986). Атомная теория многих тел. Химическая физика. 13 (2-е изд.). Springer-Verlag. ISBN 978-3-540-16649-8.

дальнейшее чтение

• G.W.F. Дрейк (2006). Справочник Springer по атомной, молекулярной и оптической физике (2-е изд.). спрингер. п. 60. ISBN 978-0-387-26308-3.
• У. Калдор; С. Уилсон (2003). Теоретическая химия и физика тяжелых и сверхтяжелых элементов. Успехи теоретической химии и физики. 11. спрингер. п. 183. ISBN 978-1-4020-1371-3.
• E.J. Brändas; P.O. Löwdin; Э. Брандас; E.S. Крячко (2004). Фундаментальный мир квантовой химии: дань памяти Пер-Олова Левдина. 3. Springer. п. 385. ISBN 978-1-4020-2583-9.
• П. Швердтфегер (2004). Теория релятивистской электронной структуры: Часть 2. Приложения.. Теоретическая и вычислительная химия. 14. Эльзевир. п. 97. ISBN 978-0-08-054047-4.
• М. Барыш; Ю. Исикава (2010). Релятивистские методы для химиков. Проблемы и достижения вычислительной химии и физики. 10. Springer. п. 311. ISBN 978-1-4020-9975-5.

• G.H.F. Дирксен; С. Уилсон (1983). Методы вычислительной молекулярной физики. Научная серия НАТО C. 113. Springer. ISBN 978-90-277-1638-5.
• Зенонас Рудзикас (2007). "8". Теоретическая атомная спектроскопия. Кембриджские монографии по атомной, молекулярной и химической физике. 7. Чикагский университет: Издательство Кембриджского университета. ISBN 978-0-521-02622-2.
• Lietuvos Fizikų draugija (2004). Lietuvos fizikos žurnalas. 44. Чикагский университет: Draugija.
• ДОМАШНИЙ ПИТОМЕЦ. Йоргенсен (1987). Операторы и теория представлений: канонические модели алгебр операторов, возникающие в квантовой механике. Чикагский университет: Эльзевир. ISBN 978-0-08-087258-2.
• П. Цвитанович (2008). Теория групп - птичьи следы, ложь и исключительные группы. Принстон, Нью-Джерси: Princeton Univ. Нажмите. ISBN 978-0-691-11836-9.

Примечания