WikiDer > Bagplot
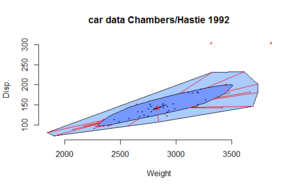
А волынка, или заговор со звездообразованием,[1][2] это метод в надежная статистика для визуализации два- или трехмерные статистические данные, аналогичные одномерным коробчатый сюжет. Представлен в 1999 г. Rousseuw и др., багплощадка позволяет визуализировать местоположение, распространение, перекос, и выбросы набора данных.[3]
строительство
Багажник состоит из трех вложенных друг в друга полигоны, называемые «мешком», «забором» и «петлей».
- Внутренний многоугольник, называемый мешок, построен на основе Глубина Тьюки, наименьшее количество наблюдений, которое может содержать полуплоскость который также содержит данную точку.[4] Он содержит не более 50% точек данных.
- Самый внешний из трех полигонов, называемый забор не нарисован как часть волынки, но используется для его построения. Он образуется при надувании мешка определенным коэффициентом (обычно 3). Наблюдения за забором помечены как выбросы.[5]
- Наблюдения, не отмеченные как выбросы, обведены значком. петля, то выпуклая оболочка наблюдений за забором.[6]
Символ звездочки (*) рядом с центром графика используется для обозначения медианы глубины, точки с максимально возможной глубиной Тьюки. Наблюдения между сумкой и ограждением отмечены отрезками линии на средней глубине, соединяющей их с сумкой.
Трехмерная версия состоит из внутренней и внешней сумки.[7] Внешний мешок должен быть окрашен в прозрачные цвета, чтобы внутренний мешок оставался видимым.
Свойства
Багаж инвариантен относительно аффинные преобразования плоскости и устойчивы к выбросам.[8]
использованная литература
- ^ Rousseeuw, Peter J .; Колеи I .; Тьюки Дж. У. (1999). "Багажник: двумерный коробчатый сюжет". Американский статистик. 53 (4): 382–387. Дои:10.1080/00031305.1999.10474494.
- ^ Рональд К. Пирсон (1 апреля 2005 г.). Несовершенные данные майнинга: работа с загрязнениями и неполными записями. СИАМ. С. 204–. ISBN 978-0-89871-582-8.
- ^ Доминик Хотон; Джонатан Хотон (18 сентября 2011 г.). Аналитика уровня жизни: развитие через призму данных обследований домашних хозяйств. Springer. С. 14–. ISBN 978-1-4614-0385-2.
- ^ Софи Дабо-Нианг; Фредерик Феррати (21 мая 2008 г.). Функциональная и операторская статистика. Springer. С. 204–. ISBN 978-3-7908-2062-1.
- ^ Джон С. Гауэр; Сугнет Гарднер Люббе; Ниль Ж. Ле Ру (23 февраля 2011 г.). Понимание биплотов. Джон Вили и сыновья. С. 59–. ISBN 978-1-119-97290-7.
- ^ Прабханджан Нараяначар Таттар (24 июля 2013 г.). Разработка статистических приложений R на примере руководства для начинающих. Пакт Паблишинг Лтд., Стр. 203–. ISBN 978-1-84951-945-8.
- ^ Kruppa, Jochen J .; Юнг К. (2017). «Автоматическая идентификация выбросов из нескольких групп в молекулярных данных с высокой пропускной способностью с использованием диаграмм и диаграмм». BMC Bioinformatics. 18: 232. Дои:10.1186 / s12859-017-1645-5. ЧВК 5414140.
- ^ Раджив Раман; Роберт Седжвик; Маттиас Ф. Столлманн (1 января 2006 г.). Труды восьмого семинара по разработке алгоритмов и экспериментов и третьего семинара по аналитической алгоритмике и комбинаторике. СИАМ. С. 62–. ISBN 978-0-89871-610-8.