WikiDer > Модель Бора

Модель торта атом водорода (Z = 1) или водородоподобный ион (Z > 1), где отрицательно заряженные электрон ограниченный атомная оболочка окружает небольшой положительно заряженный атомное ядро и когда электрон прыгает между орбитами, это сопровождается испускаемым или поглощенным количеством электромагнитная энергия (hν).^[1] Орбиты, по которым может перемещаться электрон, показаны серыми кружками; их радиус увеличивается по мере п², куда п это главное квантовое число. В 3 → 2 изображенный здесь переход дает первую строку Серия Бальмера, а для водорода (Z = 1) это приводит к фотону длина волны 656 нм (красный свет).

В атомная физика, то Модель Бора или же Модель Резерфорда-Бора, представленный Нильс Бор и Эрнест Резерфорд в 1913 году представляет собой систему, состоящую из небольшого плотного ядра, окруженного вращающимися электронами, аналогичную структуре Солнечная система, но с привлечением электростатические силы на месте сила тяжести. После кубическая модель (1902), сливовый пудинг модель (1904 г.) Сатурнианская модель (1904), а Модель Резерфорда (1911 г.) Модель Резерфорда-Бора или просто Модель Бора для краткости (1913). Улучшение по сравнению с моделью Резерфорда 1911 г. в основном касалось нового квантово-физический интерпретация.

Ключевой успех модели заключался в объяснении Формула Ридберга для спектрального эмиссионные линии атомных водород. Хотя формула Ридберга была известна экспериментально, она не получила теоретического обоснования до тех пор, пока не была представлена ​​модель Бора. Модель Бора не только объясняла причины структуры формулы Ридберга, но и обеспечивала обоснование фундаментальных физических констант, составляющих эмпирические результаты формулы.

Модель Бора - относительно примитивная модель атом водородапо сравнению с атом валентной оболочки модель. Теоретически его можно вывести как приближение первого порядка атома водорода с использованием более широкой и гораздо более точной квантовой механики и, таким образом, может рассматриваться как устаревшая научная теория. Однако из-за своей простоты и правильных результатов для выбранных систем (см. Приложение ниже) модель Бора все еще обычно преподают, чтобы познакомить студентов с квантовая механика или же диаграммы уровней энергии прежде чем перейти к более точным, но более сложным, валентной оболочки атом. Родственная модель была первоначально предложена Артур Эрих Хаас в 1910 г., но был отклонен. Квантовая теория периода между Открытие Планком кванта (1900) и появление зрелой квантовой механики (1925) часто называют старая квантовая теория.

Источник

Модель Бора, показывающая максимальное количество электронов на оболочку с оболочками, обозначенными Рентгеновское обозначение

В начале 20 века эксперименты Эрнеста Резерфорда установил, что атомы состояла из диффузного облака отрицательно заряженных электроны окружающий небольшой, плотный, положительно заряженный ядро.^[2] Учитывая эти экспериментальные данные, Резерфорд, естественно, рассмотрел планетарную модель атома, Модель Резерфорда 1911 года. Электроны вращались вокруг ядра Солнца, но возникла техническая трудность: законы классической механики (т. е. Формула лармора) предсказывают, что электрон освободит электромагнитное излучение вращаясь вокруг ядра. Поскольку электрон теряет энергию, он быстро движется по спирали внутрь, коллапсируя в ядро ​​за время около 16 пикосекунды.^[3] Эта модель атома губительна, поскольку предсказывает, что все атомы нестабильны.^[4] Кроме того, по мере того, как электроны вращаются по спирали внутрь, частота излучения будет быстро увеличиваться по мере того, как орбита становится меньше и быстрее.^{[нужна цитата]} Это вызовет непрерывный поток электромагнитного излучения. Однако эксперименты конца XIX века с электрические разряды показали, что атомы излучают свет (то есть электромагнитное излучение) только на определенных дискретных частотах.

Чтобы преодолеть проблемы атома Резерфорда, в 1913 г. Нильс Бор выдвинул три постулата, которые резюмируют большую часть его модели:

1. Электрон может вращаться по определенным стабильным орбитам вокруг ядра, не излучая никакой энергии, вопреки тому, что классический электромагнетизм предлагает. Эти стабильные орбиты называются стационарными орбитами и достигаются на определенных дискретных расстояниях от ядра. Электрон не может иметь никакой другой орбиты между дискретными.
2. Стационарные орбиты достигаются на расстояниях, на которых угловой момент вращающегося электрона кратен приведенному Постоянная Планка: ${displaystyle m_ {mathrm {e}} vr = nhbar}$, куда п = 1, 2, 3, ... называется главное квантовое число, и час = час/2π. Наименьшее значение п равно 1; это дает минимально возможный радиус орбиты 0,0529 нм, известный как Радиус Бора. Когда электрон оказывается на этой нижней орбите, он не может приблизиться к протону. Исходя из квантового правила углового момента, Бор^[2] смог вычислить энергии разрешенных орбит атома водорода и другие водородоподобный атомы и ионы. Эти орбиты связаны с определенными энергиями и также называются энергетическими оболочками или уровни энергии. На этих орбитах ускорение электрона не приводит к потере излучения и энергии. Модель атома Бора была основана на квантовой теории излучения Планка.
3. Электроны могут набирать и терять энергию, только перепрыгивая с одной разрешенной орбиты на другую, поглощая или испуская электромагнитное излучение с определенной частотой. ν определяется разностью энергий уровней согласно Соотношение Планка: ${displaystyle Delta E = E_ {2} -E_ {1} = hu}$, куда час - постоянная Планка.

Другие моменты:

1. Как и теория Эйнштейна фотоэлектрический эффект, Формула Бора предполагает, что во время квантового скачка дискретный количество энергии излучается. Однако, в отличие от Эйнштейна, Бор придерживался принципа классический Теория Максвелла электромагнитного поля. Квантование электромагнитного поля объяснялось дискретностью уровней энергии атомов; Бор не верил в существование фотоны.^[5][6]
2. Согласно теории Максвелла частота ν классического излучения равна частоте вращения ν_гнить электрона на своей орбите, с гармоники при целых кратных этой частоте. Этот результат получается из модели Бора для скачков между уровнями энергии E_п и E_п−k когда k намного меньше, чем п. Эти скачки воспроизводят частоту k-я гармоника орбиты п. При достаточно больших значениях п (так называемый Ридберг заявляет), две орбиты, участвующие в процессе излучения, имеют почти одинаковую частоту вращения, так что классическая орбитальная частота не является неоднозначной. Но для маленьких п (или большой k) частота излучения не имеет однозначной классической интерпретации. Это знаменует рождение принцип соответствия, требуя согласования квантовой теории с классической теорией только в пределе больших квантовых чисел.
3. В Теория Бора – Крамерса – Слейтера (Теория БКС) - это неудачная попытка расширить модель Бора, которая нарушает сохранение энергии и импульс в квантовых скачках, причем законы сохранения выполняются только в среднем.

Условие Бора о том, что угловой момент является целым кратным час был позже переосмыслен в 1924 г. де Бройль как стоячая волна Условие: электрон описывается волной, и по окружности орбиты электрона должно умещаться целое количество длин волн:

${displaystyle nlambda = 2pi r.}$

Согласно гипотезе де Бройля, частицы вещества, такие как электрон, ведут себя как волны. Итак, длина волны де Бройля электрона равна:

${displaystyle lambda = {frac {h} {mv}}}$.

откуда следует, что

${displaystyle {frac {nh} {mv}} = 2pi r}$

или же

${displaystyle {frac {nh} {2pi}} = mvr}$

куда ${displaystyle mvr}$ это угловой момент ${displaystyle ell}$ орбитального электрона.

${displaystyle ell = {frac {nh} {2pi}}}$

что является вторым постулатом Бора.

Бор описал угловой момент электронной орбиты как 1/2h, в то время как длина волны де Бройля из λ = час/п описал h, деленный на импульс электрона. Однако в 1913 году Бор обосновал свое правило, апеллируя к принципу соответствия, не давая никакой интерпретации волн. В 1913 году о волновом поведении частиц материи, таких как электрон, не подозревали.

В 1925 году был предложен новый вид механики, квантовая механика, в которой модель Бора электронов, движущихся по квантованным орбитам, была расширена до более точная модель движения электронов. Новая теория была предложена Вернер Гейзенберг. Другая форма той же теории, волновой механики, был открыт австрийским физиком Эрвин Шредингер независимо и по разным причинам. Шредингер использовал волны материи де Бройля, но искал волновые решения трехмерного волнового уравнения, описывающего электроны, которые были вынуждены двигаться вокруг ядра водородоподобный атом, будучи захваченным потенциалом положительного заряда ядра.

Уровни энергии электронов

Модели, изображающие уровни энергии электронов в водороде, гелии, литии и неоне

Модель Бора дает почти точные результаты только для системы, в которой две заряженные точки вращаются вокруг друг друга со скоростью, намного меньшей, чем скорость света. Это касается не только одноэлектронных систем, таких как атом водорода, однократно ионизированный гелий, и дважды ионизированный литий, но он включает позитроний и Ридберг заявляет любого атома, в котором один электрон находится далеко от всего остального. Его можно использовать для K-линия Расчеты рентгеновских переходов, если добавлены другие допущения (см. Закон Мозли ниже). В физике высоких энергий его можно использовать для расчета масс тяжелый кварк мезоны.

Расчет орбит требует двух предположений.

• Классическая механика

Электрон удерживается на круговой орбите за счет электростатического притяжения. В центростремительная сила равно Кулоновская сила.

${displaystyle {m_ {mathrm {e}} v ^ {2} over r} = {Zk_ {mathrm {e}} e ^ {2} over r ^ {2}}}$

куда м_е - масса электрона, е - заряд электрона, k_е это Кулоновская постоянная и Z атома атомный номер. Здесь предполагается, что масса ядра намного больше массы электрона (что является хорошим предположением). Это уравнение определяет скорость электрона на любом радиусе:

${displaystyle v = {sqrt {Zk_ {mathrm {e}} e ^ {2} over m_ {mathrm {e}} r}}.}$

Он также определяет полную энергию электрона на любом радиусе:

${displaystyle E = - {1 больше 2} m_ {mathrm {e}} v ^ {2}}$

Полная энергия отрицательна и обратно пропорциональна р. Это означает, что требуется энергия, чтобы оттолкнуть вращающийся электрон от протона. Для бесконечных значений р, энергия равна нулю, что соответствует неподвижному электрону, бесконечно удаленному от протона. Полная энергия составляет половину потенциальная энергия, разница в кинетической энергии электрона. Это также верно для некруглых орбит теорема вириала.

• Квантовое правило

В угловой момент L = м_еvr является целым числом, кратным час:

${displaystyle m_ {mathrm {e}} vr = nhbar}$

Вывод

Если электрон в атоме движется по орбите с периодом Т, как правило, электромагнитное излучение повторяется каждый период обращения. Если связь с электромагнитным полем слабая, так что орбита не сильно затухает за один цикл, излучение будет испускаться по схеме, которая повторяется каждый период, так что преобразование Фурье будет иметь частоты, которые только кратны 1 /Т. Это классический закон излучения: излучаемые частоты кратны 1 /Т.

В квантовой механике это излучение должно происходить в квантах света с частотами, кратными 1 /Т, так что классическая механика является приближенным описанием при больших квантовых числах. Это означает, что уровень энергии, соответствующий классической орбите периода 1 /Т должны иметь близкие энергетические уровни, которые различаются по энергии на час/Т, и они должны быть расположены на равном расстоянии около этого уровня,

${displaystyle Delta E_ {n} = {h over T (E_ {n})}.}$

Бор волновался, будет ли энергетический интервал 1 /Т лучше всего рассчитывать с периодом энергетического состояния ${displaystyle E_ {n}}$, или же ${displaystyle E_ {n + 1}}$, или какое-то среднее - в ретроспективе эта модель является лишь ведущим полуклассическим приближением.

Бор считал круговые орбиты. Классически эти орбиты должны распадаться на меньшие круги при испускании фотонов. Расстояние между круговыми орбитами можно рассчитать по формуле соответствия. Для атома водорода классические орбиты имеют период Т определяется по Третий закон Кеплера масштабироваться как р^3/2. Энергия масштабируется как 1 /р, поэтому формула расстояния между уровнями составляет

${displaystyle Delta Epropto {1 over r ^ {3 over 2}} propto E ^ {3 over 2}.}$

Можно определить уровни энергии, рекурсивно снижаясь с орбиты за орбитой, но есть короткий путь.

Угловой момент L масштабов круговой орбиты как √р. Тогда энергия в единицах углового момента равна

${displaystyle Epropto {1 over r} propto {1 over L ^ {2}}}$.

Предполагая вместе с Бором, что квантованные значения L равномерно распределены, расстояние между соседними энергиями равно

${displaystyle Delta Epropto {1 over (L + hbar) ^ {2}} - {1 over L ^ {2}} приблизительно - {2hbar over L ^ {3}} propto -E ^ {3 over 2}.}$

Это желательно для равноотстоящих угловых моментов. Если следить за константами, интервал будет час, поэтому угловой момент должен быть целым числом, кратным час,

${displaystyle L = {nh over 2pi} = nhbar ~.}$

Так Бор пришел к своей модели.

Подстановка выражения для скорости дает уравнение для р с точки зрения п:

${displaystyle m_ {ext {e}} {sqrt {dfrac {k_ {ext {e}} Ze ^ {2}} {m_ {ext {e}} r}}} r = nhbar}$

так что допустимый радиус орбиты при любом п является:

${displaystyle r_ {n} = {n ^ {2} hbar ^ {2} над Zk_ {mathrm {e}} e ^ {2} m_ {mathrm {e}}}}$

Наименьшее возможное значение р в атоме водорода (Z = 1) называется Радиус Бора и равно:

${displaystyle r_ {1} = {hbar ^ {2} over k_ {mathrm {e}} e ^ {2} m_ {mathrm {e}}} примерно 5,29 imes 10 ^ {- 11} mathrm {m}}$

Энергия п-й уровень для любого атома определяется радиусом и квантовым числом:

${displaystyle E = - {Zk_ {mathrm {e}} e ^ {2} over 2r_ {n}} = - {Z ^ {2} (k_ {mathrm {e}} e ^ {2}) ^ {2} m_ {mathrm {e}} более 2hbar ^ {2} n ^ {2}} приблизительно {-13.6Z ^ {2} более n ^ {2}} mathrm {eV}}$

Электрон на низшем энергетическом уровне водорода (п = 1) поэтому имеет около 13,6эВ меньше энергии, чем у неподвижного электрона, бесконечно удаленного от ядра. Следующий энергетический уровень (п = 2) составляет −3,4 эВ. Третий (п = 3) составляет −1,51 эВ и т. Д. Для больших значений п, это также энергии связи высоковозбужденного атома с одним электроном на большой круговой орбите вокруг остальной части атома. Формула водорода также совпадает с формулой Уоллис продукт.^[7]

Комбинация естественных констант в формуле энергии называется ридберговской энергией (р_E):

${displaystyle R_ {mathrm {E}} = {(k_ {mathrm {e}} e ^ {2}) ^ {2} m_ {mathrm {e}} более 2hbar ^ {2}}}$

Это выражение поясняется интерпретацией его в комбинациях, которые образуют больше натуральные единицы:

${displaystyle, m_ {mathrm {e}} c ^ {2}}$ это энергия покоя электрона (511 кэВ)

${displaystyle, {k_ {mathrm {e}} e ^ {2} over hbar c} = alpha приблизительно {1 over 137}}$ это постоянная тонкой структуры

${displaystyle, R_ {mathrm {E}} = {1 over 2} (m_ {mathrm {e}} c ^ {2}) alpha ^ {2}}$

Поскольку этот вывод основан на предположении, что ядро ​​вращается вокруг одного электрона, мы можем обобщить этот результат, позволив ядру иметь заряд q = Ze, куда Z это атомный номер. Теперь это даст нам уровни энергии для водородных (водородоподобных) атомов, которые могут служить грубым приближением по порядку величины фактических уровней энергии. Итак, для ядер с Z протонов уровни энергии (в грубом приближении):

${displaystyle E_ {n} = - {Z ^ {2} R_ {mathrm {E}} над n ^ {2}}}$

Реальные уровни энергии не могут быть решены аналитически для более чем одного электрона (см. ппроблема тела), потому что на электроны влияет не только ядро но также взаимодействуют друг с другом через Кулоновская сила.

Когда Z = 1/α (Z ≈ 137) движение становится в высшей степени релятивистским, и Z² отменяет α² в р; энергия орбиты начинает быть сопоставимой с энергией покоя. Достаточно большие ядра, если бы они были стабильными, уменьшили бы свой заряд, создав связанный электрон из вакуума, выбрасывая позитрон на бесконечность. Это теоретическое явление экранирования электромагнитного заряда, которое предсказывает максимальный заряд ядра. Эмиссия таких позитронов наблюдалась при столкновениях тяжелых ионов с образованием временных сверхтяжелых ядер.^[8]

Формула Бора правильно использует уменьшенная масса электрона и протона во всех ситуациях, а не массы электрона,

${displaystyle m_ {ext {red}} = {frac {m_ {mathrm {e}} m_ {mathrm {p}}} {m_ {mathrm {e}} + m_ {mathrm {p}}}} = m_ {mathrm) {e}} ~ {frac {1} {1 + m_ {mathrm {e}} / m_ {mathrm {p}}}} ~.}$

Однако эти числа почти одинаковы из-за гораздо большей массы протона, примерно в 1836,1 раз больше массы электрона, так что приведенная масса в системе равна массе электрона, умноженной на константу 1836,1 / ( 1 + 1836,1) = 0,99946. Этот факт исторически важен для того, чтобы убедить Резерфорда в важности модели Бора, поскольку он объясняет тот факт, что частоты линий в спектрах однократно ионизованного гелия отличаются от частот линий водорода не ровно в 4 раза, а скорее в 4 раза. умноженное на отношение приведенной массы для систем водорода и гелия, что было намного ближе к экспериментальному соотношению, чем ровно 4.

Для позитрония в формуле также используется приведенная масса, но в данном случае это точно масса электрона, деленная на 2. При любом значении радиуса электрон и позитрон движутся с половинной скоростью вокруг своего общего центра. масса, и каждый имеет только четверть кинетической энергии. Полная кинетическая энергия вдвое меньше, чем у отдельного электрона, движущегося вокруг тяжелого ядра.

${displaystyle E_ {n} = {R_ {mathrm {E}} более 2n ^ {2}} ~~~~~~}$ (позитроний)

Формула Ридберга

Формула Ридберга, которая была эмпирически известна до формулы Бора, рассматривается в теории Бора как описывающая энергии переходов или квантовые скачки между орбитальными энергетическими уровнями. Формула Бора дает численное значение уже известного и измеренного Постоянная Ридберга, но с точки зрения более фундаментальных констант природы, включая заряд электрона и Постоянная Планка.

Когда электрон перемещается с исходного уровня энергии на более высокий, он затем перепрыгивает на каждый уровень, пока не переместится в исходное положение, что приводит к испусканию фотона. Используя полученную формулу для различных уровней энергии водорода, можно определить длины волн света, которые может излучать атом водорода.

Энергия фотона, испускаемого атомом водорода, определяется разностью двух уровней энергии водорода:

${displaystyle E = E_ {i} -E_ {f} = R_ {mathrm {E}} left ({frac {1} {n_ {f} ^ {2}}} - {frac {1} {n_ {i}) ^ {2}}} право),}$

куда п_ж конечный уровень энергии, и п_я - начальный уровень энергии.

Поскольку энергия фотона равна

${displaystyle E = {frac {hc} {lambda}} ,,}$

длина волны испускаемого фотона определяется выражением

${displaystyle {frac {1} {lambda}} = Rleft ({frac {1} {n_ {f} ^ {2}}} - {frac {1} {n_ {i} ^ {2}}} ight). ,}$

Это известно как Формула Ридберга, а постоянная Ридберга р является р_E/hc, или же р_E/2π в натуральные единицы. Эта формула была известна в XIX веке ученым, изучающим спектроскопия, но не было теоретического объяснения этой формы или теоретического предсказания значения р, до Бора. Фактически, вывод Бора постоянной Ридберга, а также сопутствующее согласие формулы Бора с экспериментально наблюдаемыми спектральными линиями Lyman (п_ж =1), Балмер (п_ж = 2), и Пашен (п_ж = 3) и успешное теоретическое предсказание других линий, которые еще не наблюдались, было одной из причин, по которой его модель была немедленно принята.

Для применения к атомам с более чем одним электроном формулу Ридберга можно изменить, заменив Z с Z − б или же п с п − б куда б постоянная, представляющая эффект экранирования из-за внутренней оболочки и других электронов (см. Электронная оболочка и более позднее обсуждение «Оболочечной модели атома» ниже). Это было установлено эмпирически до того, как Бор представил свою модель.

Модель оболочки (более тяжелые атомы)

Бор расширил модель водорода, чтобы дать приближенную модель для более тяжелых атомов. Это дало физическую картину, которая впервые воспроизводила многие известные атомные свойства.

У более тяжелых атомов больше протонов в ядре и больше электронов, которые нейтрализуют заряд. Идея Бора заключалась в том, что каждая дискретная орбита могла удерживать только определенное количество электронов. После того, как эта орбита заполнится, нужно будет использовать следующий уровень. Это дает атому структура оболочки, в котором каждая оболочка соответствует орбите Бора.

Эта модель даже более приближена, чем модель водорода, потому что она рассматривает электроны в каждой оболочке как невзаимодействующие. Но отталкивание электронов несколько учитывается явлением скрининг. Электроны на внешних орбитах не только вращаются вокруг ядра, но они также перемещаются вокруг внутренних электронов, поэтому эффективный заряд Z, который они ощущают, уменьшается на количество электронов на внутренней орбите.

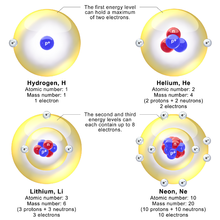
Например, у атома лития два электрона находятся на самой нижней орбите 1s, и эти электроны вращаются на Z = 2. Каждый видит ядерный заряд Z = 3 минус экранирующий эффект другого, что грубо снижает заряд ядра на 1 единицу. Это означает, что самые внутренние электроны вращаются примерно на 1/2 радиуса Бора. Самый внешний электрон на орбите лития находится примерно на радиусе Бора, поскольку два внутренних электрона уменьшают заряд ядра на 2. Этот внешний электрон должен находиться на расстоянии примерно одного радиуса Бора от ядра. Поскольку электроны сильно отталкиваются друг от друга, описание эффективного заряда очень приблизительное; эффективный заряд Z обычно не бывает целым числом. Но Закон Мозли экспериментально исследует самую внутреннюю пару электронов и показывает, что они действительно видят ядерный заряд приблизительно Z - 1, в то время как наиболее удаленный электрон в атоме или ионе с одним электроном на внешней оболочке вращается вокруг ядра с эффективным зарядом Z − k куда k - полное количество электронов во внутренних оболочках.

Оболочечная модель смогла качественно объяснить многие загадочные свойства атомов, которые были систематизированы в конце 19 века в периодическая таблица элементов. Одним из свойств был размер атомов, который можно было приблизительно определить, измерив вязкость газов и плотности чистых кристаллических тел. Атомы имеют тенденцию уменьшаться в размерах вправо в периодической таблице и становиться намного больше в следующей строке таблицы. Атомы справа от таблицы стремятся получить электроны, а атомы слева - их терять. Каждый элемент в последнем столбце таблицы химически инертен (благородный газ).

В модели оболочки это явление объясняется заполнением оболочки.Последовательные атомы становятся меньше, потому что они заполняют орбиты одного и того же размера, пока орбита не заполнится, и в этот момент следующий атом в таблице имеет слабо связанный внешний электрон, заставляющий его расширяться. Первая орбита Бора заполнена, когда на ней есть два электрона, что объясняет, почему гелий инертен. Вторая орбита пропускает восемь электронов, и когда она заполнена, атом становится неоновым, снова инертным. Третья орбиталь снова содержит восемь, за исключением того, что в более правильной трактовке Зоммерфельда (воспроизведенной в современной квантовой механике) есть дополнительные «d» электроны. Третья орбита может содержать дополнительные 10 d электронов, но эти позиции не заполняются, пока не будут заполнены еще несколько орбиталей со следующего уровня (заполнение n = 3 d орбиталей дает 10 переходные элементы). Неравномерное заполнение - это эффект взаимодействий между электронами, которые не учитываются ни в моделях Бора, ни в моделях Зоммерфельда и которые трудно вычислить даже в современной трактовке.

Закон и расчет Мозли (K-альфа рентгеновские эмиссионные линии)

Нильс Бор сказал в 1962 году: «Видите ли, на самом деле работа Резерфорда не была воспринята всерьез. Мы не можем понять сегодня, но ее вообще не воспринимали всерьез. Нигде о ней не упоминалось. Великая перемена произошла от Мозли».^[9]

В 1913 г. Генри Мозли обнаружили эмпирическую связь между самой сильной рентгеновской линией, испускаемой атомами при электронной бомбардировке (тогда известной как К-альфа линия), а их атомный номер Z. Было обнаружено, что эмпирическая формула Мозли выводима из формулы Ридберга и Бора (на самом деле Мозли упоминает только Эрнест Резерфорд и Антониус Ван ден Брук с точки зрения моделей). Два дополнительных предположения, что [1] эта рентгеновская линия возникла при переходе между уровнями энергии с квантовыми числами 1 и 2, и [2], что атомный номер Z при использовании в формуле для атомов тяжелее водорода, должно быть уменьшено на 1, чтобы (Z − 1)².

Мозли написал Бору, озадаченный своими результатами, но Бор не смог помочь. В то время он думал, что постулируемая самая внутренняя «К» -оболочка электронов должна иметь по крайней мере четыре электрона, а не два, которые точно объяснили бы результат. Поэтому Мозли опубликовал свои результаты без теоретического объяснения.

Позже люди поняли, что эффект был вызван экранированием заряда внутренней оболочкой, содержащей всего 2 электрона. В эксперименте один из самых внутренних электронов в атоме выбивается, оставляя вакансию на самой нижней боровской орбите, которая содержит единственный оставшийся электрон. Затем эта вакансия заполняется электроном со следующей орбиты, у которой n = 2. Но n = 2 электрона видят эффективный заряд Z - 1, что соответствует заряду ядра, когда один электрон остается на самой нижней боровской орбите, чтобы экранировать заряд ядра.Z, и уменьшите его на -1 (из-за того, что отрицательный заряд электрона экранирует положительный заряд ядра). Энергия, полученная электроном, падающим со второй оболочки на первую, дает закон Мозли для линий K-альфа:

${displaystyle E = hu = E_ {i} -E_ {f} = R_ {mathrm {E}} (Z-1) ^ {2} left ({frac {1} {1 ^ {2}}} - {frac {1} {2 ^ {2}}} ночь),}$

или же

${displaystyle f = u = R_ {mathrm {v}} left ({frac {3} {4}} ight) (Z-1) ^ {2} = (2,46 imes 10 ^ {15} operatorname {Hz}) ( Z-1) ^ {2}.}$

Здесь, р_v = р_E/час - постоянная Ридберга, в единицах частоты, равная 3,28 x 10¹⁵ Гц. Для значений Z между 11 и 31 это последнее соотношение было получено эмпирическим путем Мозли на простом (линейном) графике квадратного корня из частоты рентгеновского излучения в зависимости от атомного номера (однако для серебра Z = 47 экспериментально полученное значение срок проверки заменить на 0,4). Несмотря на ограниченный срок действия,^[10] Закон Мозли не только установил объективное значение атомного номера, но, как заметил Бор, он также сделал больше, чем вывод Ридберга, чтобы установить справедливость ядерной модели атома Резерфорда / Ван ден Брука / Бора с атомным номером (место на периодическая таблица), обозначающая целые единицы ядерного заряда.

В К-альфа Линия времени Мозли теперь известна как пара близких линий, записанная как (Kα₁ и Kα₂) в Обозначение Зигбана.

Недостатки

Модель Бора дает неверное значение L=час для орбитального углового момента в основном состоянии: Из эксперимента известно, что угловой момент в истинном основном состоянии равен нулю.^[11] Хотя ментальные образы несколько терпят неудачу на этих уровнях масштаба, можно думать, что электрон на самой низкой современной «орбитали» без орбитального момента вообще не вращается «вокруг» ядра, а просто плотно обходит его в эллипс с нулевой площадью (это можно изобразить как «вперед и назад», без ударов и взаимодействия с ядром). Это воспроизводится только в более сложной полуклассической обработке, такой как у Зоммерфельда. Тем не менее, даже самая сложная полуклассическая модель не может объяснить того факта, что состояние с наименьшей энергией является сферически симметричным - оно не указывает в каком-либо конкретном направлении.

Тем не менее в современном полностью квантовая обработка в фазовом пространстве, правильная деформация (осторожное полное растяжение) полуклассического результата подстраивает значение углового момента до правильного эффективного. Как следствие, выражение физического основного состояния получается посредством сдвига выражения исчезающего квантового углового момента, которое соответствует сферической симметрии.

В современной квантовой механике электрон в водороде - это сферическое облако вероятности которая становится плотнее возле ядра. Константа скорости распада вероятности в водороде равна обратной величине радиуса Бора, но поскольку Бор работал с круговыми орбитами, а не с эллипсами с нулевой площадью, тот факт, что эти два числа точно совпадают, считается «совпадением». (Тем не менее, существует много таких совпадений между полуклассическим и полным квантово-механическим подходом к атому; они включают идентичные уровни энергии в атоме водорода и вывод постоянной тонкой структуры, которая возникает из релятивистской модели Бора-Зоммерфельда ( см. ниже) и который, как оказалось, соответствует совершенно другой концепции в полной современной квантовой механике).

Модель Бора также сталкивается с трудностями или не может объяснить:

• Большая часть спектров более крупных атомов. В лучшем случае он может делать прогнозы относительно K-альфа и некоторых L-альфа спектров рентгеновского излучения для более крупных атомов, если два делаются дополнительные специальные допущения. Спектры излучения атомов с одним электроном на внешней оболочке (атомы в литий group) также можно приблизительно предсказать. Кроме того, если известны эмпирические факторы электронно-ядерного экранирования для многих атомов, многие другие спектральные линии могут быть выведены из информации в аналогичных атомах различных элементов с помощью принципов комбинации Ритца – Ридберга (см. Формула Ридберга). Все эти методы по существу используют ньютоновскую картину энергетического потенциала атома Бора.
• относительные интенсивности спектральных линий; хотя в некоторых простых случаях формула Бора или ее модификации могли дать разумные оценки (например, расчеты Крамерса для Эффект Старка).
• Существование тонкая структура и сверхтонкая структура в спектральных линиях, которые, как известно, возникают из-за множества релятивистских и тонких эффектов, а также осложнений, связанных со спином электрона.
• В Эффект Зеемана - изменения спектральных линий из-за внешних магнитные поля; они также связаны с более сложными квантовыми принципами, взаимодействующими со спиновыми и орбитальными магнитными полями электронов.
• Модель также нарушает принцип неопределенности в том смысле, что он считает, что у электронов есть известные орбиты и местоположение - две вещи, которые нельзя измерить одновременно.
• Дублеты и триплеты появляются в спектрах некоторых атомов как очень близкие пары линий. Модель Бора не может сказать, почему некоторые уровни энергии должны находиться очень близко друг к другу.
• Многоэлектронные атомы не имеют уровней энергии, предсказываемых моделью. Это не работает для (нейтрального) гелия.

Доработки

Эллиптические орбиты с одинаковой энергией и квантованным угловым моментом

Было предложено несколько усовершенствований модели Бора, в первую очередь Модели Зоммерфельда или Бора – Зоммерфельда, который предполагает, что электроны движутся по эллиптическим орбитам вокруг ядра, а не по круговым орбитам модели Бора.^[1] Эта модель дополняла условие квантованного углового момента модели Бора дополнительным условием радиального квантования, Уилсон–Зоммерфельд условие квантования.^[12][13]

${displaystyle int _ {0} ^ {T} p_ {r}, dq_ {r} = nh,}$

куда п_р - радиальный импульс, канонически сопряженный координате q что является радиальным положением и Т один полный орбитальный период. Интеграл - это действие из координаты угла действия. Это условие, предложенное принцип соответствия, является единственно возможным, поскольку квантовые числа равны адиабатические инварианты.

Модель Бора – Зоммерфельда была принципиально противоречивой и приводила ко многим парадоксам. В магнитное квантовое число измерил наклон плоскости орбиты относительно ху-самолет, и он мог принимать только несколько дискретных значений. Это противоречило очевидному факту, что атом можно поворачивать в разные стороны относительно координат без ограничений. Квантование Зоммерфельда может выполняться в разных канонических координатах и ​​иногда дает разные ответы. Включение поправок на излучение было трудным, потому что требовалось найти координаты действие-угол для комбинированной системы излучение / атом, что затруднительно, когда излучению позволяли выходить. Вся теория не распространялась на неинтегрируемые движения, а это означало, что многие системы нельзя было рассматривать даже в принципе. В конце концов, модель была заменена современной квантово-механической обработкой атом водорода, который впервые был дан Вольфганг Паули в 1925 г., используя метод Гейзенберга матричная механика. Современная картина атома водорода основана на атомные орбитали из волновая механика который Эрвин Шредингер Разработан в 1926 году.

Однако это не означает, что модель Бора-Зоммерфельда не имела успеха. Расчеты, основанные на модели Бора – Зоммерфельда, смогли точно объяснить ряд более сложных атомных спектральных эффектов. Например, до первого порядка возмущения, модель Бора и квантовая механика делают одинаковые предсказания для расщепления спектральных линий в эффекте Штарка. Однако при возмущениях более высокого порядка модель Бора и квантовая механика различаются, и измерения эффекта Штарка при высокой напряженности поля помогли подтвердить правильность квантовой механики над моделью Бора. Преобладающая теория, стоящая за этим различием, заключается в формах орбиталей электронов, которые меняются в зависимости от энергетического состояния электрона.

Условия квантования Бора – Зоммерфельда вызывают вопросы в современной математике. Согласованное условие квазиклассического квантования требует определенного типа структуры фазового пространства, что накладывает топологические ограничения на типы симплектических многообразий, которые можно квантовать. В частности, симплектическая форма должна быть форма кривизны из связь из Эрмитский линейный пакет, который называется предварительное квантование.

Бор также обновил свою модель в 1922 году, предположив, что определенное количество электронов (например, 2, 8 и 18) соответствует стабильному "закрытые оболочки".^[14]

Модель химической связи

Нильс Бор предложил модель атома и модель химической связи. По его модели для двухатомная молекулаэлектроны атомов молекулы образуют вращающееся кольцо, плоскость которого перпендикулярна оси молекулы и равноудалена от ядер атомов. В динамическое равновесие молекулярной системы достигается за счет баланса сил между силами притяжения ядер к плоскости кольца электронов и силами взаимного отталкивания ядер. Модель химической связи Бора учитывала Кулоновское отталкивание - электроны в кольце находятся на максимальном расстоянии друг от друга.^[15][16]

Смотрите также

Рекомендации

Эта статья имеет нечеткий стиль цитирования. Используемые ссылки можно сделать более ясными с помощью другого или последовательного стиля цитата и сноска. (Август 2020 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Сноски

Основные источники

• Нильс Бор (1913). «О строении атомов и молекул, часть I» (PDF). Философский журнал. 26 (151): 1–24. Bibcode:1913ПМаг ... 26 .... 1Б. Дои:10.1080/14786441308634955.
• Нильс Бор (1913). «О строении атомов и молекул, часть II. Системы, содержащие только одно ядро» (PDF). Философский журнал. 26 (153): 476–502. Bibcode:1913ПМаг ... 26..476Б. Дои:10.1080/14786441308634993.
• Нильс Бор (1913). «О строении атомов и молекул, часть III. Системы, содержащие несколько ядер». Философский журнал. 26: 857–875. Bibcode:1913ПМаг ... 26..857Б. Дои:10.1080/14786441308635031.
• Нильс Бор (1914). «Спектры гелия и водорода». Природа. 92 (2295): 231–232. Bibcode:1913Натура..92..231Б. Дои:10.1038 / 092231d0. S2CID 11988018.
• Нильс Бор (1921). «Атомная структура». Природа. 107 (2682): 104–107. Bibcode:1921Натура.107..104Б. Дои:10.1038 / 107104a0. S2CID 4035652.
• А. Эйнштейн (1917). "Zum Quantensatz von Sommerfeld und Epstein". Verhandlungen der Deutschen Physikalischen Gesellschaft. 19: 82–92. Перепечатано в Сборник статей Альберта Эйнштейна, Переводчик А. Энгеля, (1997) Princeton University Press, Princeton. 6 п. 434. (обеспечивает элегантную переформулировку условий квантования Бора – Зоммерфельда, а также важное понимание квантования неинтегрируемых (хаотических) динамических систем.)

дальнейшее чтение

• Линус Карл Полинг (1970). «Глава 5-1». Общая химия (3-е изд.). Сан-Франциско: W.H. Freeman & Co.
  • Перепечатка: Линус Полинг (1988). Общая химия. Нью-Йорк: Dover Publications. ISBN 0-486-65622-5.
• Георгий Гамов (1985). "Глава 2". Тридцать лет, потрясших физику. Dover Publications.
• Вальтер Дж. Леманн (1972). «Глава 18». Атомная и молекулярная структура: развитие наших концепций. Джон Уайли и сыновья. ISBN 0-471-52440-9.
• Пол Типлер и Ральф Ллевеллин (2002). Современная физика (4-е изд.). В. Х. Фриман. ISBN 0-7167-4345-0.
• Клаус Хентшель: Elektronenbahnen, Quantensprünge und Spektren, в: Charlotte Bigg & Jochen Hennig (ред.) Atombilder. Ikonografien des Atoms in Wissenschaft und Öffentlichkeit des 20. Jahrhunderts, Göttingen: Wallstein-Verlag 2009, pp. 51–61
• Стивен и Сьюзан Зумдал (2010). «Глава 7.4». Химия (8-е изд.). Брукс / Коул. ISBN 978-0-495-82992-8.
• Хельге Краг (2011). «Концептуальные возражения против атомной теории Бора - есть ли у электронов« свобода воли »?». Европейский физический журнал H. 36 (3): 327–352. Bibcode:2011EPJH ... 36..327K. Дои:10.1140 / epjh / e2011-20031-x. S2CID 120859582.

внешняя ссылка

• Стоячие волны в атомной модели Бора Интерактивное моделирование для интуитивного объяснения условия квантования стоячих волн в атомной моде Бора

Викискладе есть медиафайлы по теме Модель Бора.