WikiDer > Диффузная МРТ

Диффузная МРТ
Цветовая карта DTI
MeSH	D038524

Диффузионно-взвешенная магнитно-резонансная томография (DWI или же DW-MRI) - это использование конкретных Последовательности МРТ а также программное обеспечение, которое генерирует изображения из полученных данных, использующих диффузию молекул воды для создания контраст в МР-изображениях.^[1][2][3] Это позволяет отображать распространение процесс молекул, в основном воды, в биологические ткани, in vivo и неинвазивно. Молекулярная диффузия в тканях не является бесплатной, но отражает взаимодействие со многими препятствиями, такими как макромолекулы, волокна и мембраны. Таким образом, модели диффузии молекул воды могут выявить микроскопические детали структуры тканей, как в нормальном, так и в болезненном состоянии. Особый вид DWI, диффузионная тензорная визуализация (DTI), широко использовался для отображения белое вещество трактография в мозгу.

Вступление

В диффузионно-взвешенная визуализация (DWI), интенсивность каждого элемента изображения (воксель) отражает наилучшую оценку скорости диффузии воды в этом месте. Поскольку подвижность воды обусловлена ​​тепловым возбуждением и сильно зависит от ее клеточного окружения, гипотеза, лежащая в основе DWI, заключается в том, что результаты могут указывать на (ранние) патологические изменения. Например, DWI более чувствителен к ранним изменениям после инсульта, чем более традиционные измерения МРТ, такие как Т1 или же T2 релаксация тарифы. Вариант диффузионно-взвешенной визуализации, визуализация спектра диффузии (DSI),^[4] использовался при получении наборов данных Connectome; DSI - это вариант визуализации, взвешенной по диффузии, которая чувствительна к внутривоксельной неоднородности в направлениях диффузии, вызванной пересечением трактов волокна, и, таким образом, позволяет более точно отображать аксональный траектории, чем другие подходы к диффузионной визуализации.^[5]

Распространенные изображения очень полезны для диагностики сосудистых инсультов в головном мозге. Он также все чаще используется в постановке немелкоклеточный рак легкого, где серьезный кандидат на замену позитронно-эмиссионная томография как «золотой стандарт» для этого типа заболеваний. Диффузионная тензорная визуализация разрабатывается для изучения заболеваний белое вещество мозга, а также для исследования других тканей организма (см. ниже). DWI наиболее применим, когда в интересующей ткани преобладает изотропное движение воды, например серое вещество в кора головного мозга и основные ядра мозга, или в теле, где скорость диффузии кажется одинаковой при измерении по любой оси. Однако DWI также остается чувствительным к релаксации T1 и T2. Чтобы запутать эффекты диффузии и релаксации на контрасте изображения, можно получить количественные изображения коэффициента диффузии или, точнее, кажущегося коэффициента диффузии (ADC). Концепция ADC была введена, чтобы принять во внимание тот факт, что процесс диффузии в биологических тканях сложен и отражает несколько различных механизмов.^[6]

Визуализация тензора диффузии (DTI) важен, когда ткань, такая как нервная аксоны из белое вещество в головном мозге или мышечных волокнах сердца - имеет внутреннюю волокнистую структуру, аналогичную анизотропия некоторых кристаллов. Тогда вода будет диффундировать быстрее в направлении, совпадающем с внутренней структурой, и медленнее, когда она будет двигаться перпендикулярно предпочтительному направлению. Это также означает, что измеренная скорость диффузии будет отличаться в зависимости от направления, с которого смотрит наблюдатель.

Традиционно в диффузионно-взвешенной визуализации (DWI) применяются три градиентных направления, достаточных для оценки следа тензора диффузии или «среднего коэффициента диффузии», предполагаемой меры отек. Клинически взвешенные изображения оказались очень полезными для диагностики сосудов. удары в головном мозге путем раннего обнаружения (в течение нескольких минут) гипоксического отека.^[7]

Более расширенное сканирование DTI извлекает информацию о направлении нервного тракта из данных с использованием трехмерных или многомерных векторных алгоритмов на основе шести или более направлений градиента, достаточных для вычисления диффузии. тензор. Модель тензора диффузии - это довольно простая модель процесса диффузии, предполагающая однородность и линейность диффузии в каждом вокселе изображения.^[7] Из тензора диффузии измеряется анизотропия диффузии, такая как фракционная анизотропия (FA), можно вычислить. Более того, главное направление тензора диффузии можно использовать для вывода о связности белого вещества мозга (т.е. трактография; пытаясь увидеть, какая часть мозга связана с какой другой частью).

Недавно были предложены более продвинутые модели диффузионного процесса, цель которых преодолеть слабые места модели тензора диффузии. Среди прочего, они включают визуализацию q-пространства. ^[8] и отображение обобщенного тензора диффузии.

Механизм

Диффузионная визуализация - это МРТ метод, который создает магнитно-резонансные изображения in vivo биологических тканей, сенсибилизированных локальными характеристиками молекулярной диффузии, обычно воды (но других части также могут быть исследованы с использованием подходов МР-спектроскопии).^[9]МРТ можно сделать чувствительной к движению молекул. Регулярное получение МРТ использует поведение протонов в воде для создания контраста между клинически значимыми характеристиками конкретного объекта. Универсальный характер МРТ обусловлен этой способностью создавать контраст, связанный со структурой тканей на микроскопическом уровне. В типичном ${ displaystyle T_ {1}}$На взвешенном изображении молекулы воды в образце возбуждаются при наложении сильного магнитного поля. Это заставляет многие протоны в молекулах воды прецессировать одновременно, создавая сигналы на МРТ. В ${ displaystyle T_ {2}}$-взвешенные изображения, контраст получается путем измерения потери когерентности или синхронизации между протонами воды. Когда вода находится в среде, где она может свободно падать, релаксация занимает больше времени. В определенных клинических ситуациях это может создавать контраст между областью патологии и окружающей здоровой тканью.

Чтобы сделать изображения МРТ чувствительными к диффузии, напряженность магнитного поля (B1) линейно изменяется с помощью градиента импульсного поля. Поскольку прецессия пропорциональна силе магнита, протоны начинают прецессировать с разной скоростью, что приводит к дисперсии фазы и потере сигнала. Применяется еще один градиентный импульс той же величины, но с противоположным направлением, чтобы перефокусировать или перефазировать спины. Перефокусировка не будет идеальной для протонов, которые двигались в течение интервала времени между импульсами, и сигнал, измеренный аппаратом МРТ, уменьшается. Этот метод «импульса градиента поля» был первоначально разработан для ЯМР Стейскалом и Таннером. ^[10] который вывел уменьшение сигнала из-за применения градиента импульса, связанного с величиной диффузии, которая происходит, с помощью следующего уравнения:

${ displaystyle { frac {S (TE)} {S_ {0}}} = exp left [- gamma ^ {2} G ^ {2} delta ^ {2} left ( Delta - { frac { delta} {3}} right) D right]}$

куда ${ displaystyle S_ {0}}$ - интенсивность сигнала без диффузионного взвешивания, ${ displaystyle S}$ - сигнал с градиентом, ${ displaystyle gamma}$ это гиромагнитное отношение, ${ displaystyle G}$ - сила градиентного импульса, ${ displaystyle delta}$ - длительность импульса, ${ displaystyle Delta}$ время между двумя импульсами, и, наконец, ${ displaystyle D}$ - коэффициент диффузии.

Чтобы локализовать это ослабление сигнала для получения изображений диффузии, необходимо объединить импульсные импульсы градиента магнитного поля, используемые для МРТ (направленные на локализацию сигнала, но эти градиентные импульсы слишком слабы, чтобы вызвать ослабление, связанное с диффузией) с дополнительным " «зондирование движения» градиентных импульсов по методу Стейскала и Таннера. Эта комбинация нетривиальна, поскольку между всеми импульсами градиента возникают перекрестные члены. Уравнение, установленное Стейскалом и Таннером, затем становится неточным, и ослабление сигнала должно быть рассчитано либо аналитически, либо численно, интегрируя все градиентные импульсы, присутствующие в последовательности МРТ, и их взаимодействия. Результат быстро становится очень сложным, учитывая большое количество импульсов, присутствующих в последовательности МРТ, и для упрощения Ле Бихан предложил собрать все градиентные составляющие в «b-фактор» (который зависит только от параметров сбора данных), чтобы ослабление сигнала просто становится:^[1]

${ displaystyle { frac {S (TE)} {S_ {0}}} = exp (-b cdot ADC)}$

Кроме того, коэффициент диффузии, ${ displaystyle D}$, заменяется кажущимся коэффициентом диффузии, ${ displaystyle ADC}$, чтобы указать, что процесс диффузии не является свободным в тканях, но затруднен и модулируется многими механизмами (ограничение в замкнутых пространствах, извилистость вокруг препятствий и т. д.) и что другие источники некогерентного движения IntraVoxel (IVIM), такие как кровоток в небольших сосуды или спинномозговая жидкость в желудочках также вносят свой вклад в ослабление сигнала. В конце концов, изображения «взвешиваются» в процессе диффузии: на этих диффузно-взвешенных изображениях (DWI) сигнал тем сильнее ослабляется, чем быстрее происходит диффузия, и чем больше b фактор есть. Однако эти взвешенные по диффузии изображения по-прежнему чувствительны к релаксационному контрасту T1 и T2, что иногда может сбивать с толку. Можно рассчитать "чистые" карты диффузии (или, точнее, карты АЦП, где АЦП является единственным источником контраста), собирая изображения как минимум с двумя различными значениями, ${ displaystyle b_ {1}}$ и ${ displaystyle b_ {2}}$, фактора b согласно:

${ displaystyle mathrm {ADC} (x, y, z) = ln [S_ {2} (x, y, z) / S_ {1} (x, y, z)] / (b_ {1} - Би 2})}$

Хотя эта концепция ADC оказалась чрезвычайно успешной, особенно для клинического применения, в последнее время она подверглась сомнению, поскольку были введены новые, более полные модели диффузии в биологических тканях. Эти модели стали необходимыми, поскольку распространение в тканях не является бесплатным. В этом состоянии АЦП, кажется, зависит от выбора значений b (кажется, что АЦП уменьшается при использовании больших значений b), так как график ln (S / So) не является линейным с коэффициентом b, как и ожидалось из над уравнениями. Это отклонение от поведения свободной диффузии - вот что делает диффузионную МРТ столь успешной, поскольку ADC очень чувствителен к изменениям микроструктуры ткани. С другой стороны, моделирование диффузии в тканях становится очень сложным. Среди наиболее популярных моделей - биэкспоненциальная модель, которая предполагает наличие двух водоемов в медленном или промежуточном обмене. ^[11][12] и модель кумулянтного расширения (также называемая эксцессом),^[13][14][15]что не обязательно требует наличия 2 бассейнов.

Модель диффузии

Учитывая концентрацию ${ displaystyle rho}$ и поток ${ displaystyle J}$, Первый закон Фика дает связь между потоком и концентрацией градиент:

${ Displaystyle J (х, т) = - D набла ро (х, т)}$

где D - коэффициент диффузии. Тогда при сохранении массы уравнение неразрывности связывает производную концентрации по времени с расхождение флюса:

${ Displaystyle { frac { partial rho (x, t)} { partial t}} = - nabla cdot J (x, t)}$

Соединяя их вместе, мы получаем уравнение диффузии:

${ displaystyle { frac { partial rho (x, t)} { partial t}} = D nabla ^ {2} rho (x, t).}$

Динамика намагничивания

В отсутствие диффузии изменение ядерной намагничивание с течением времени определяется классической Уравнение Блоха

${ displaystyle { frac {d { vec {M}}} {dt}} = gamma { vec {M}} times { vec {B}} - { frac {M_ {x} { vec {i}} + M_ {y} { vec {j}}} {T_ {2}}} - { frac {(M_ {z} -M_ {0}) { vec {k}}} { Т_ {1}}}}$

в котором есть члены для прецессии, T2 релаксации и T1 релаксации.

В 1956 г. H.C. Торри математически показал, как Уравнения Блоха поскольку намагниченность изменится с добавлением диффузии.^[16] Торри модифицировал оригинальное описание Блоха поперечной намагниченности, включив в него условия диффузии и применение пространственно изменяющегося градиента. Поскольку намагниченность ${ displaystyle M}$ - вектор, существует 3 уравнения диффузии, по одному для каждого измерения. В Уравнение Блоха-Торри является:

${ displaystyle { frac {d { vec {M}}} {dt}} = gamma { vec {M}} times { vec {B}} - { frac {M_ {x} { vec {i}} + M_ {y} { vec {j}}} {T_ {2}}} - { frac {(M_ {z} -M_ {0}) { vec {k}}} { T_ {1}}} + nabla cdot { vec {D}} nabla { vec {M}}}$

куда ${ displaystyle D}$ теперь тензор диффузии.

В простейшем случае, когда диффузия изотропна, тензор диффузии кратен тождеству:

${ displaystyle {D} = { vec {D}} cdot { vec {I}} = { vec {D}} cdot { begin {bmatrix} 1 & 0 & 0 0 & 1 & 0 0 & 0 & 1 end {bmatrix }},}$

то уравнение Блоха-Торри будет иметь решение

${ displaystyle {M} = {M} _ { text {bloch}} e ^ {- { frac {1} {3}} gamma ^ {2} G ^ {2} t ^ {3} D} sim e ^ {- bD_ {0}}}$

Экспоненциальный член будет называться затухание ${ displaystyle A}$. Анизотропная диффузия будет иметь аналогичное решение для тензора диффузии, за исключением того, что будет измеряться кажущийся коэффициент диффузии (АЦП). В целом затухание составляет:

${ Displaystyle А = е ^ {- сумма _ {я, j} b_ {ij} D_ {ij}}}$

где ${ displaystyle b_ {ij}}$ термины включают поля градиента ${ displaystyle G_ {x}}$, ${ displaystyle G_ {y}}$, и ${ displaystyle G_ {z}}$.

Оттенки серого

Стандартная шкала серого для изображений DWI предназначена для более яркого представления увеличенного ограничения диффузии.^[17]

Применение DWI

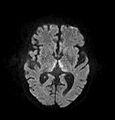
Чаще всего обычный DWI (без DTI) применяется при острой ишемии головного мозга. DWI напрямую визуализирует ишемический некроз в инфаркт мозга в виде цитотоксического отека,^[18] появляется как высокий сигнал DWI в течение нескольких минут после артериальной окклюзии.^[19] С перфузионная МРТ обнаружение как сердечника инфаркта, так и спасаемого полутень, последнее можно количественно оценить с помощью DWI и перфузионной МРТ.^[20]

• 

  DWI показывает некроз (показан более ярким) в инфаркт мозга

• 

  DWI показывает ограниченную диффузию в мезиальных дорсальных таламусах, соответствующую Энцефалопатия Вернике

• 

  DWI показывает кортикальный ленточный высокий сигнал, соответствующий ограничению диффузии у пациента с известным Синдром MELAS

Еще одна область применения DWI - онкология. Опухоли во многих случаях являются высококлеточными, обеспечивая ограниченную диффузию воды, и поэтому появляются с относительно высокой интенсивностью сигнала в DWI.^[21] DWI обычно используется для обнаружения и сцена опухолей, а также для отслеживания реакции опухоли на лечение с течением времени. DWI также можно собирать для визуализации всего тела с помощью метода, называемого «диффузионно-взвешенная визуализация всего тела с подавлением фонового сигнала тела» (DWIBS).^[22]

Изображение АЦП

Изображение ADC того же случая церебрального инфаркта, которое видно на DWI в разделе выше

An кажущийся коэффициент диффузии (ADC) изображение или Карта АЦП, представляет собой МРТ-изображение, которое более точно показывает диффузию, чем обычный DWI, за счет устранения Взвешивание Т2 что в остальном присуще обычному DWI.^[23] Визуализация ADC делает это путем получения нескольких обычных изображений DWI с разным весом DWI, а изменение сигнала пропорционально скорости диффузии. В отличие от изображений DWI, стандартная шкала оттенков серого для изображений ADC представляет меньшую величину диффузии как более темную.^[17]

Инфаркт головного мозга приводит к ограничению диффузии, и поэтому разница между изображениями с различным взвешиванием DWI будет незначительной, что приведет к изображению ADC с низким сигналом в области инфаркта.^[23] Снижение ADC может быть обнаружено через несколько минут после инфаркта мозга.^[24] Высокий сигнал инфаркта ткани на обычном DWI является результатом его частичного взвешивания T2.^[25]

Визуализация тензора диффузии

Диффузионная тензорная визуализация (DTI) - это метод магнитно-резонансной томографии, который позволяет измерять ограниченную диффузию воды в ткани для получения изображений нервного тракта вместо использования этих данных исключительно с целью присвоения контраста или цвета пикселям в кресте. -секционное изображение. Он также предоставляет полезную структурную информацию о мышцах, включая сердечную мышцу, а также о других тканях, таких как простата.^[26]

В DTI каждый воксель имеет одну или несколько пар параметров: скорость диффузии и предпочтительное направление диффузии, описываемое в терминах трехмерного пространства, для которого этот параметр действителен. Свойства каждого воксела одного изображения DTI обычно вычисляются векторной или тензорной математикой из шести или более различных измерений, взвешенных по диффузии, каждая из которых получена с различной ориентацией градиентов, повышающих чувствительность к диффузии. В некоторых методах выполняются сотни измерений, каждое из которых составляет полное изображение, для создания единого результирующего расчетного набора данных изображения. Более высокая информативность вокселя DTI делает его чрезвычайно чувствительным к тонким патологиям мозга. Кроме того, информация о направлении может использоваться на более высоком уровне структуры для выбора и отслеживания нейронных трактов через мозг - процесс, называемый трактография.^[27]

Более точное определение процесса получения изображения заключается в том, что интенсивность изображения в каждой позиции ослабляется в зависимости от силы (б-значение) и направление так называемого градиента магнитной диффузии, а также от локальной микроструктуры, в которой диффундируют молекулы воды. Чем более ослаблено изображение в данном положении, тем больше диффузия в направлении градиента диффузии. Чтобы измерить полный профиль диффузии ткани, необходимо повторить МРТ-сканирование, применяя разные направления (и, возможно, силы) градиента диффузии для каждого сканирования.

Меры анизотропии и диффузии

Визуализация данных DTI с помощью эллипсоидов.

В современной клинической неврологии различные патологии головного мозга могут быть лучше всего обнаружены путем анализа конкретных показателей анизотропии и диффузии. Основной физический процесс распространение заставляет группу молекул воды выходить из центральной точки и постепенно достигать поверхности эллипсоид если среда анизотропна (в случае изотропной среды это была бы поверхность шара). Формализм эллипсоида действует также как математический метод организации тензорных данных. Измерение тензора эллипсоида позволяет провести ретроспективный анализ, чтобы собрать информацию о процессе диффузии в каждом вокселе ткани.^[28]

В изотропной среде, такой как спинномозговая жидкостьмолекулы воды движутся за счет диффузии и движутся с одинаковой скоростью во всех направлениях. Зная подробные эффекты градиентов диффузии, мы можем создать формулу, которая позволяет нам преобразовывать сигнал затухание вокселя МРТ в числовую меру диффузии - коэффициент диффузии D. Когда различные препятствия и ограничивающие факторы, такие как клеточные мембраны и микротрубочки мешают свободной диффузии, мы измеряем «кажущийся коэффициент диффузии», или АЦП, потому что измерение не учитывает все локальные эффекты и рассматривает затухание, как если бы все скорости движения были вызваны исключительно Броуновское движение. ADC в анизотропной ткани варьируется в зависимости от направления, в котором он измеряется. Распространение происходит быстро по длине (параллельно) аксон, и медленнее перпендикулярно ему.

После того, как мы измерили воксель с шести или более направлений и скорректировали затухание из-за эффектов T2 и T1, мы можем использовать информацию из нашего рассчитанного тензора эллипсоида для описания того, что происходит в вокселе. Если вы рассмотрите эллипсоид, сидящий под углом в Декартово grid, то вы можете рассмотреть проекцию этого эллипса на три оси. Три проекции могут дать вам АЦП по каждой из трех осей АЦП._Икс, АЦП_у, АЦП_z. Это приводит к идее описания среднего коэффициента диффузии в вокселе, который будет просто

${ displaystyle (ADC_ {x} + ADC_ {y} + ADC_ {z}) / 3 = ADC_ {i}}$

Мы используем я нижний индекс, чтобы обозначить, что это то, каким будет коэффициент изотропной диффузии с усредненными эффектами анизотропии.

У самого эллипсоида есть главная длинная ось, а затем еще две маленькие оси, которые описывают его ширину и глубину. Все три перпендикулярны друг другу и пересекаются в центральной точке эллипсоида. Мы называем оси в этой настройке собственные векторы и меры их длины собственные значения. Длины обозначаются греческой буквой. λ. Длинный, указывающий в направлении аксона, будет λ₁ и две маленькие оси будут иметь длину λ₂ и λ₃. В настройке тензорного эллипсоида DTI мы можем рассматривать каждый из них как меру коэффициента диффузии вдоль каждой из трех основных осей эллипсоида. Это немного отличается от АЦП, так как это была проекция на ось, а λ является фактическим измерением рассчитанного нами эллипсоида.

Коэффициент диффузии вдоль главной оси, λ₁ также называется продольной диффузией или осевая диффузия или даже параллельный коэффициент диффузии λ_∥. Исторически это ближе всего к тому, что Ричардс первоначально измерил с длиной вектора в 1991 году.^[29] Коэффициенты диффузии по двум второстепенным осям часто усредняются, чтобы получить меру радиальный коэффициент диффузии

${ displaystyle lambda _ { perp} = ( lambda _ {2} + lambda _ {3}) / 2.}$

Эта величина является оценкой степени ограничения из-за мембран и других эффектов и оказывается чувствительной мерой дегенеративной патологии при некоторых неврологических состояниях.^[30] Его также можно назвать перпендикулярным коэффициентом диффузии (${ displaystyle lambda _ { perp}}$).

Другой часто используемый показатель, который суммирует общий коэффициент диффузии, - это След- сумма трех собственных значений,

${ displaystyle mathrm {tr} ( Lambda) = lambda _ {1} + lambda _ {2} + lambda _ {3}}$

куда ${ displaystyle Lambda}$ диагональная матрица с собственными значениями ${ displaystyle lambda _ {1}}$, ${ displaystyle lambda _ {2}}$ и ${ displaystyle lambda _ {3}}$ по его диагонали.

Если разделить эту сумму на три, мы получим средний коэффициент диффузии,

${ displaystyle mathrm {MD} = ( lambda _ {1} + lambda _ {2} + lambda _ {3}) / 3}$

что равно АЦП_я поскольку

${ displaystyle { begin {align} mathrm {tr} ( Lambda) / 3 & = mathrm {tr} (VV ^ {- 1} Lambda) / 3 & = mathrm {tr} (V Лямбда V ^ {- 1}) / 3 & = mathrm {tr} (D) / 3 & = ADC_ {i} end {выровнено}}}$

куда ${ displaystyle V}$ - матрица собственных векторов и ${ displaystyle D}$ - тензор диффузии. Помимо описания степени диффузии, часто важно описать относительную степень анизотропии в вокселе. На одном конце будет сфера изотропной диффузии, а на другом - очень тонкая сигара или карандаш. вытянутый сфероид. Простейшая мера получается делением самой длинной оси эллипсоида на самую короткую = (λ₁/λ₃). Однако оказалось, что это очень чувствительно к шуму измерения, поэтому были разработаны все более комплексные меры для захвата меры при минимизации шума. Важным элементом этих расчетов является сумма квадратов разностей коэффициентов диффузии = (λ₁ − λ₂)² + (λ₁ − λ₃)² + (λ₂ − λ₃)². Мы используем квадратный корень из суммы квадратов, чтобы получить своего рода средневзвешенное значение, в котором преобладает самый большой компонент. Одна из целей состоит в том, чтобы сохранить число около 0, если воксель сферический, и около 1, если он удлиненный. Это приводит к фракционная анизотропия или же FA который представляет собой квадратный корень из суммы квадратов (SRSS) разностей коэффициентов диффузии, деленной на SRSS коэффициентов диффузии. Когда вторая и третья оси малы по отношению к главной оси, число в числителе почти равно числу в знаменателе. Мы также умножаем на ${ displaystyle 1 / { sqrt {2}}}$ так что FA имеет максимальное значение 1. Вся формула для FA выглядит так:

${ displaystyle mathrm {FA} = { frac { sqrt {3 (( lambda _ {1} - operatorname {E} [ lambda]) ^ {2} + ( lambda _ {2} - имя оператора {E} [ lambda]) ^ {2} + ( lambda _ {3} - operatorname {E} [ lambda]) ^ {2})}} { sqrt {2 ( lambda _ {1 } ^ {2} + lambda _ {2} ^ {2} + lambda _ {3} ^ {2})}}}}$

Дробную анизотропию также можно разделить на линейные, плоские и сферические меры в зависимости от «формы» диффузионного эллипсоида.^[31][32] Например, вытянутый эллипсоид в форме «сигары» указывает на строго линейную анизотропию, «летающую тарелку» или сплюснутый сфероид представляет собой диффузию в плоскости, а сфера указывает на изотропную диффузию, равную во всех направлениях.^[33] Если собственные значения вектора диффузии отсортированы так, что ${ displaystyle lambda _ {1} geq lambda _ {2} geq lambda _ {3} geq 0}$, то меры можно рассчитать следующим образом:

Для линейный случай, куда ${ displaystyle lambda _ {1} gg lambda _ {2} simeq lambda _ {3}}$,

${ displaystyle C_ {l} = { frac { lambda _ {1} - lambda _ {2}} { lambda _ {1} + lambda _ {2} + lambda _ {3}}}}$

Для плоский корпус, куда ${ displaystyle lambda _ {1} simeq lambda _ {2} gg lambda _ {3}}$,

${ displaystyle C_ {p} = { frac {2 ( lambda _ {2} - lambda _ {3})} { lambda _ {1} + lambda _ {2} + lambda _ {3} }}}$

Для сферический корпус, куда ${ displaystyle lambda _ {1} simeq lambda _ {2} simeq lambda _ {3}}$,

${ displaystyle C_ {s} = { frac {3 lambda _ {3}} { lambda _ {1} + lambda _ {2} + lambda _ {3}}}}$

Каждая мера находится между 0 и 1, и их сумма равна единице. Дополнительный мера анизотропии может использоваться для описания отклонения от сферического случая:

${ displaystyle C_ {a} = C_ {l} + C_ {p} = 1-C_ {s} = { frac { lambda _ {1} + lambda _ {2} -2 lambda _ {3} } { lambda _ {1} + lambda _ {2} + lambda _ {3}}}}$

Используются и другие показатели анизотропии, в том числе относительная анизотропия (РА):

${ displaystyle mathrm {RA} = { frac { sqrt {( lambda _ {1} - operatorname {E} [ lambda]) ^ {2} + ( lambda _ {2} - operatorname { E} [ lambda]) ^ {2} + ( lambda _ {3} - operatorname {E} [ lambda]) ^ {2}}} {{ sqrt {3}} operatorname {E} [ lambda]}}}$

и Соотношение объемов (VR):

${ displaystyle mathrm {VR} = { frac { lambda _ {1} lambda _ {2} lambda _ {3}} { operatorname {E} [ lambda] ^ {3}}}}$

Приложения

Эта секция нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. (Декабрь 2013) (Узнайте, как и когда удалить этот шаблон сообщения)

Основное применение - получение изображений белое вещество где расположение, ориентация и анизотропия трактов можно измерить. Архитектура аксоны в параллельных пучках, а их миелин ножны, облегчают распространение молекул воды предпочтительно вдоль их основного направления. Такая преимущественно ориентированная диффузия называется анизотропная диффузия.

Трактографическая реконструкция нейронных связей с помощью DTI

Видеть https://doi.org/10.3389/fsurg.2020.00019 для дополнительной информации

Визуализация этого свойства является расширением диффузной МРТ. Если серия градиентов диффузии (т.е. магнитное поле вариации магнита МРТ), которые могут определять по крайней мере 3 направленных вектора (использование 6 различных градиентов является минимальным, а дополнительные градиенты повышают точность для "недиагональной" информации), можно рассчитать для каждого воксель, а тензор (т.е. симметричный положительно определенный 3 × 3 матрица), описывающий трехмерную форму диффузии. Направление волокна указывается основным тензором собственный вектор. Этот вектор может быть закодирован цветом, что дает картографию положения и направления трактов (красный для левого-правого, синий для верхнего-нижнего и зеленый для передне-заднего).^[34] Яркость взвешивается по фракционной анизотропии, которая является скалярной мерой степени анизотропии в данном вокселе. Средний коэффициент диффузии (MD) или след - это скалярная мера общей диффузии в вокселе. Эти меры обычно используются в клинической практике для локализации поражений белого вещества, которые не обнаруживаются на других формах клинической МРТ.^[35]

Приложения в мозгу:

• Локализация белого вещества в тракте поражения таких как травма и определение степени тяжести диффузная черепно-мозговая травма. Локализация опухоли в отношении трактов белого вещества (инфильтрация, отклонение) было одним из самых важных начальных приложений. При хирургическом планировании некоторых типов опухоли головного мозга, операции помогает знание близости и относительного положения кортикоспинальный тракт и опухоль.
• Данные визуализации тензора диффузии могут использоваться для выполнения трактография в белом веществе. Алгоритмы отслеживания волокна могут использоваться для отслеживания волокна по всей его длине (например, кортикоспинальный тракт, через которые передается моторная информация от моторная кора к спинной мозг и периферийные нервы). Трактография - полезный инструмент для измерения дефицита белого вещества, например, при старении. Его оценка ориентации и силы волокон становится все более точной и имеет широкое потенциальное применение в областях когнитивной нейробиологии и нейробиологии.
• Использование DTI для оценки белого вещества при развитии, патологии и дегенерации было в центре внимания более 2500 исследовательских публикаций с 2005 г. Он обещает быть очень полезным для различения Болезнь Альцгеймера из других типов слабоумие. Приложения в исследованиях мозга включают исследование нейронные сети in vivo, а также в коннектомика.

Приложения для периферических нервов:

• Плечевое сплетение: DTI может различать нормальные нервы^[36] (как показано на трактограмме спинного мозга и плечевого сплетения и реконструкции 3D 4k Вот) от травматически поврежденных нервных корешков.^[37]
• Синдром кубитального туннеля: показатели, полученные на основе DTI (FA и RD), могут отличить бессимптомных взрослых от пациентов с компрессией локтевого нерва в локтевом суставе.^[38]
• Синдром запястного канала: Показатели, полученные на основе DTI (более низкий FA и MD), отличают здоровых взрослых от людей с синдром запястного канала^[39]

Математическая основа - тензоры

Диффузионная МРТ основана на математических и физических интерпретациях геометрических величин, известных как тензоры. Только частный случай общего математического понятия имеет отношение к отображению, которое основано на концепции симметричная матрица.^{[примечания 1]} Сама диффузия является тензорной, но во многих случаях цель состоит не в том, чтобы попытаться изучить диффузию мозга как таковую, а в том, чтобы просто попытаться использовать преимущества диффузной анизотропии в белом веществе с целью определения ориентации аксонов и величины или степень анизотропии. Тензоры реально существуют в материале или ткани, поэтому они не перемещаются, когда система координат, используемая для их описания, вращается. Существует множество различных возможных представлений тензора (ранга 2), но среди них это обсуждение фокусируется на эллипсоиде из-за его физического отношения к диффузии и из-за его исторического значения в развитии визуализации диффузионной анизотропии в МРТ.

Следующая матрица отображает компоненты тензора диффузии:

${ displaystyle { bar {D}} = { begin {vmatrix} D _ { color {red} xx} & D_ {xy} & D_ {xz} D_ {xy} & D _ { color {red} yy} & D_ {yz} D_ {xz} & D_ {yz} & D _ { color {красный} zz} end {vmatrix}}}$

Одна и та же матрица чисел может одновременно использоваться во второй раз для описания формы и ориентации эллипса, а одна и та же матрица чисел может одновременно использоваться третьим способом для матричной математики для сортировки собственных векторов и собственных значений, как описано ниже.

Физические тензоры

Идея тензора в физической науке возникла из попыток описать количество физических свойств. Первыми свойствами, к которым они были применены, были те, которые можно описать одним числом, например, температура. Свойства, которые можно описать таким образом, называются скаляры; их можно рассматривать как тензоры ранга 0 или тензоры 0-го порядка. Тензоры также можно использовать для описания величин, которые имеют направленность, например механическую силу. Эти величины требуют указания как величины, так и направления и часто обозначаются значком вектор. Трехмерный вектор можно описать тремя компонентами: его проекцией на Икс, у, и z топоры. Векторы такого типа можно рассматривать как тензоры ранга 1 или тензоры 1-го порядка.

Тензор часто является физическим или биофизическим свойством, определяющим взаимосвязь между двумя векторами. Когда к объекту прикладывается сила, может возникнуть движение. Если движение происходит в одном направлении, преобразование можно описать с помощью вектора - тензора ранга 1. Однако в ткани диффузия приводит к движению молекул воды по траекториям, которые проходят во многих направлениях во времени, что приводит к сложная проекция на декартовы оси. Этот рисунок воспроизводится, если одинаковые условия и силы применяются к одной и той же ткани одинаковым образом. Если существует внутренняя анизотропная организация ткани, которая ограничивает диффузию, то этот факт будет отражен в модели диффузии. Связь между свойствами движущей силы, которая вызывает диффузию молекул воды, и результирующей картиной их движения в ткани может быть описана тензором. Совокупность молекулярных смещений этого физического свойства может быть описана девятью компонентами, каждая из которых связана с парой осей. хх, гг, zz, ху, yx, xz, zx, yz, зы.^[40] Их можно записать в виде матрицы, аналогичной той, что приведена в начале этого раздела.

Аналогичным образом ведет себя диффузия от точечного источника в анизотропной среде белого вещества. Первый импульс градиента диффузии Стейскала Таннера эффективно маркирует некоторые молекулы воды, а второй импульс эффективно показывает их смещение из-за диффузии. Каждое примененное направление градиента измеряет движение вдоль направления этого градиента. Шесть или более градиентов суммируются, чтобы получить все измерения, необходимые для заполнения матрицы, при условии, что она симметрична выше и ниже диагонали (красные нижние индексы).

В 1848 г. Анри Юро де Сенармон^[41] прикладывал нагретый острие к полированной поверхности кристалла, покрытой воском. В некоторых материалах, имеющих «изотропную» структуру, кольцо расплава будет распространяться по поверхности по кругу. В анизотропных кристаллах разброс имел форму эллипса. В трех измерениях этот разброс представляет собой эллипсоид. В качестве Адольф Фик Как было показано в 1850-х годах, диффузия демонстрирует многие из тех же моделей, что и при передаче тепла.

Математика эллипсоидов

На этом этапе полезно рассмотреть математику эллипсоидов. Эллипсоид можно описать формулой: топор² + к² + cz² = 1. Это уравнение описывает квадрика поверхность. Относительные значения а, б, и c определить, описывает ли квадрика эллипсоид или гиперболоид.

Оказывается, можно добавить еще три компонента: топор² + к² + cz² + dyz + ezx + fxy = 1. Множество комбинаций а, б, c, d, е, и ж по-прежнему описывают эллипсоиды, но дополнительные компоненты (d, е, ж) описывают поворот эллипсоида относительно ортогональных осей декартовой системы координат. Эти шесть переменных могут быть представлены матрицей, аналогичной тензорной матрице, определенной в начале этого раздела (поскольку диффузия симметрична, то нам нужно только шесть вместо девяти компонентов - компоненты под диагональными элементами матрицы такие же, как компоненты выше диагонали). Именно это имеется в виду, когда утверждается, что компоненты матрицы тензора второго порядка могут быть представлены эллипсоидом - если значения диффузии шести членов квадратичного эллипсоида помещаются в матрицу, это генерирует эллипсоид под углом вне ортогональной сетки. Его форма будет более вытянутой при высокой относительной анизотропии.

Когда эллипсоид / тензор представлен матрица, мы можем применить полезную технику из стандартной матричной математики и линейной алгебры, то есть "диагонализировать«матрица. Это имеет два важных значения при визуализации. Идея состоит в том, что есть два эквивалентных эллипсоида - одинаковой формы, но с разным размером и ориентацией. Первый - это измеренный эллипсоид диффузии, расположенный под углом, определяемым аксонами, и второй идеально сочетается с тремя Декартово топоры. Термин «диагонализация» относится к трем компонентам матрицы по диагонали от верхнего левого угла до нижнего правого (компоненты с красными нижними индексами в матрице в начале этого раздела). Переменные топор², к², и cz² расположены по диагонали (красные индексы), но переменные d, е и ж находятся «вне диагонали». Затем становится возможным выполнить этап векторной обработки, на котором мы переписываем нашу матрицу и заменяем ее новой матрицей, умноженной на три разных вектора единичной длины (длина = 1.0). Матрица диагонализована, потому что все недиагональные компоненты теперь равны нулю. Углы поворота, необходимые для достижения этой эквивалентной позиции, теперь появляются в трех векторах и могут быть считаны как Икс, у, и z компоненты каждого из них. Эти три вектора называются "собственные векторы"или характеристические векторы. Они содержат информацию об ориентации исходного эллипсоида. Три оси эллипсоида теперь находятся непосредственно вдоль основных ортогональных осей системы координат, поэтому мы можем легко определить их длину. Эти длины являются собственными значениями или характеристическими значениями.

Диагонализация матрицы выполняется путем нахождения второй матрицы, на которую она может быть умножена с последующим умножением на инверсию второй матрицы, при этом результатом является новая матрица, в которой три диагональных (хх, гг, zz) компоненты имеют номера, но недиагональные компоненты (ху, yz, zx) равны 0. Вторая матрица дает собственный вектор Информация.

За пределами DTI

В начале разработки трактографии на основе DTI ряд исследователей указали на недостаток модели тензора диффузии. Тензорный анализ предполагает, что есть единственный эллипсоид в каждом визуализирующем вокселе - как если бы все аксоны, проходящие через воксель, двигались в одном и том же направлении.^[42] Часто это так, но можно оценить, что более чем в 30% вокселов в изображении мозга со стандартным разрешением есть по крайней мере два разных нейронных тракта, которые проходят в разных направлениях и проходят друг через друга. В классической модели диффузионного тензора эллипсоида информация из пересекающего тракта просто появляется как шум или необъяснимое уменьшение анизотропии в данном вокселе. Дэвид Тач был одним из первых, кто описал решение этой проблемы.^[43][44] Идею лучше всего понять, если концептуально разместить геодезический купол вокруг каждого вокселя изображения. Этот икосаэдр обеспечивает математическую основу для прохождения большого числа равномерно распределенных градиентных траекторий через воксель, каждая из которых совпадает с одной из вершин икосаэдра. По сути, теперь мы собираемся смотреть на воксель с большого количества разных направлений (обычно 40 или более). Мы используем "п-tuple " мозаика добавить более равномерно расположенные вершины к исходному икосаэдру (20 граней) - идея, которая также имела свои прецеденты в исследованиях палеомагнетизма несколькими десятилетиями ранее.^[45] Мы просто хотим знать, в каких направлениях наблюдается максимальная анизотропная диффузия. Если имеется один тракт, будет только два максимума, указывающие в противоположных направлениях. Если два тракта пересекаются в вокселе, будет две пары максимумов и так далее. Мы по-прежнему можем использовать тензорную математику, чтобы использовать максимумы для выбора групп градиентов для упаковки в несколько разных тензорных эллипсоидов в одном и том же вокселе, или использовать более сложный тензорный анализ более высокого ранга,^[46] или мы можем провести настоящий «свободный от модели» анализ, который просто выбирает максимумы и продолжает трактографию.

Метод трактографии Q-Ball - это реализация, в которой Дэвид Туч предлагает математическую альтернативу тензорной модели.^[47] Вместо того, чтобы помещать данные диффузионной анизотропии в группу тензоров, используемая математика использует как распределения вероятностей, так и классический элемент геометрической томография и векторная математика появилась почти 100 лет назад - Функ преобразование Радона.^[48]

Резюме

Для DTI обычно можно использовать линейная алгебра, матричная математика и векторная математика для обработки анализа тензорных данных.

В некоторых случаях интересен полный набор тензорных свойств, но для трактография обычно необходимо знать только величину и ориентацию первичной оси или вектора. Эта первичная ось - с наибольшей длиной - является наибольшим собственным значением, и ее ориентация кодируется в соответствующем собственном векторе. Требуется только одна ось, так как предполагается, что наибольшее собственное значение совмещено с направлением основного аксона для выполнения трактографии.

Смотрите также

• Коннектом
• Трактография
• Коннекограмма

Примечания

Рекомендации

внешняя ссылка

Викискладе есть медиафайлы по теме Диффузионная магнитно-резонансная томография.

• PNRC: О диффузионной МРТ
• Атлас белого вещества