WikiDer > Барьер деления
| Ядерная физика |
|---|
 |
| Ядро · Нуклоны (п, п) · Ядерное дело · Ядерная сила · Ядерная структура · Ядерная реакция |
Нуклидыклассификация Изотопы - равный Z Изобары - равный А Изотоны - равный N Исодиаферы - равный N − Z Изомеры - равно всем вышеперечисленным Зеркальные ядра – Z ↔ N Стабильный · Магия · Даже странно · Гало (Борромео) |
Ядерная стабильность |
Высокоэнергетические процессы |
Термоядерная реакция Процессы: Звездный · Большой взрыв · Сверхновая звезда Нуклиды: Изначальный · Космогенный · Искусственный |
Альварес · Беккерель · Быть · А. Бор · Н. Бор · Чедвик · Кокрофт · Ir. Кюри · Пт. Кюри · Число Пи. Кюри · Склодовская-Кюри · Дэвиссон · Ферми · Хан · Дженсен · Лоуренс · Майер · Meitner · Олифант · Оппенгеймер · Proca · Перселл · Раби · Резерфорд · Soddy · Strassmann · Ąwitecki · Сцилард · Кассир · Томсон · Уолтон · Вигнер |
В ядерная физика и ядерная химия, то барьер деления это энергия активации требуется для ядро атома претерпеть деление. Этот барьер также можно определить как минимальное количество энергии, необходимое для деформации ядра до точки, в которой оно безвозвратно передается в процесс деления. Энергия для преодоления этого барьера может поступать либо от нейтрон бомбардировка ядра, когда дополнительная энергия нейтрона переводит ядро в возбужденное состояние и подвергается деформации, или через спонтанное деление, где ядро уже находится в возбужденном и деформированном состоянии.
Важно отметить, что попытки понять процессы деления все еще продолжаются и представляют собой очень сложную проблему для решения с тех пор, как деление было впервые обнаруженоЛиз Мейтнер Отто Хан и Фриц Штрассманн в 1938 г.[2] Хотя физики-ядерщики понимают многие аспекты процесса деления, в настоящее время не существует всеобъемлющей теоретической основы, которая дала бы удовлетворительное изложение основных наблюдений.
Разрыв
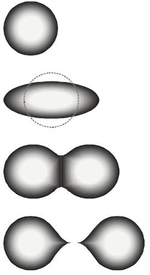
Процесс деления можно понять, когда ядро с некоторой равновесной деформацией поглощает энергию (через захват нейтронов, например), возбуждается и деформируется до конфигурации, известной как конфигурация «переходного состояния» или «седловой точки». По мере деформации ядра кулоновская энергия ядра уменьшается, а поверхностная энергия ядра увеличивается. В седловой точке скорость изменения кулоновской энергии равна скорости изменения поверхностной энергии ядра. Формирование и окончательный распад этого ядра переходного состояния является этапом, определяющим скорость в процессе деления, и соответствует переходу через энергетический барьер активации для реакции деления. Когда это происходит, перемычка между возникающими фрагментами исчезает, а ядро разделяется на два фрагмента. Точка, в которой это происходит, называется «точкой разрыва».[3]
Модель жидкой капли
Из описания начала процесса деления до «точки разрыва» очевидно, что изменение формы ядра связано с каким-либо изменением энергии. Фактически, это изменение двух типов энергии: (1) макроскопическая энергия, связанная с объемными свойствами ядра, определяемая модель капли жидкости и (2) квантово-механическая энергия, связанная с заполнением орбиталей модели оболочки.[4] Для объемных свойств ядра с небольшими искажениями поверхность, , и кулон, , энергии определяются как:
куда и - поверхностная и кулоновская энергии неискаженных сферических капель соответственно, - параметр квадрупольного искажения. При изменении кулоновской и поверхностной энергий (, ) равны, ядро становится неустойчивым по отношению к делению. В этот момент соотношение между неискаженной поверхностью и кулоновской энергией становится:
куда называется параметром делимости. Если , энергия жидкой капли уменьшается с увеличением , что приводит к делению. Если , то энергия жидкой капли уменьшается с уменьшением , что приводит к сферической форме ядра.
Кулоновскую и поверхностную энергии однородно заряженной сферы можно аппроксимировать следующими выражениями:
куда это атомный номер ядра, это массовое число ядра, это заряд электрона, - радиус неискаженного сферического ядра, - поверхностное натяжение на единицу площади ядра, и . Тогда уравнение для параметра делимости становится следующим образом:
где отношение постоянной упоминается как . Делимость данного ядра затем может быть отнесена к категории . В качестве примера, плутоний-239 имеет значение 36,97, а менее делящиеся ядра, такие как висмут-209 есть значение 32,96.
Для всех стабильных ядер должно быть меньше 1. В этом случае полная энергия деформации ядер при делении увеличится на величину , поскольку ядро деформируется в сторону деления. Это увеличение потенциальной энергии можно рассматривать как энергетический барьер активации для реакции деления. Однако современные расчеты потенциальной энергии деформации для модели жидкой капли включают множество координат деформации, помимо и представляют собой основные вычислительные задачи.
Исправления оболочки
Чтобы получить более разумные значения ядерных масс в модели жидкой капли, необходимо учитывать оболочечные эффекты. Советский физик Вилен Струтинский предложил такой метод, использующий «оболочечную коррекцию» и поправки на спаривание ядер к модели жидкой капли.[5] В этом методе полная энергия ядра принимается как сумма энергии модели жидкой капли, , оболочка, , и спаривание, , поправки к этой энергии как:
Оболочечные поправки, как и энергия жидкой капли, зависят от деформации ядра. Оболочечные поправки имеют тенденцию понижать массы основного состояния сферических ядер с магическими или почти магическими числами нейтроны и протоны. Они также имеют тенденцию к снижению массы основного состояния ядер средней оболочки при некоторой конечной деформации, что объясняет деформированный характер ядра. актиниды. Без этих оболочечных эффектов нельзя было бы наблюдать самые тяжелые ядра, поскольку они распадались бы в результате спонтанного деления на временном масштабе, намного меньшем, чем мы можем наблюдать.
Эта комбинация макроскопической жидкой капли и микроскопических оболочечных эффектов предсказывает, что для ядер в U-Пу области будет возникать двугорбый барьер деления с равной высотой барьера и глубокий вторичный минимум. Для более тяжелых ядер, например калифорний, прогнозируется, что первый барьер будет намного больше второго, и скорость прохождения через первый барьер определяется. В целом, существует множество экспериментальных и теоретических доказательств того, что путь с наименьшей энергией в процессе деления соответствует тому, что ядро, первоначально в аксиально-симметричной и масс (отражательной) симметричной форме, проходит через первый максимум в барьере деления с аксиально-асимметричным но масс-симметричной формы, а затем пройти через второй максимум в преграде с аксиально-симметричной, но масс (отражающей) асимметричной формой. Из-за сложной многомерности процесса деления не существует простых формул для высоты барьера деления. Однако существуют обширные таблицы экспериментальных характеристик высоты барьера деления для различных ядер.[4][6]
Смотрите также
Рекомендации
- ^ Л. Яффе (1968). "Ядерное деление". Ядерная химия. II. Нью-Йорк: Academic Press. КАК В B0066F5SQE.
- ^ Х. Г. Гретцер (1964). «Открытие ядерного деления». Американский журнал физики. 32: 9–15. Дои:10.1119/1.1970127.
- ^ Б. Д. Уилкинс; Э. П. Стейнберг и Р. Р. Часман (1976). «Модель точки разрыва ядерного деления на основе эффектов деформированной оболочки». Физический обзор C. 14 (5): 1832–1863. Дои:10.1103 / PhysRevC.14.1832.
- ^ а б Р. Ванденбош и Дж. Р. Хьюзенга (1974). Ядерное деление. Нью-Йорк: Academic Press. КАК В B012YSETDY.
- ^ В. М. Струтинский (1967). «Оболочечные эффекты в ядерных массах и энергиях деформации». Ядерная физика A. 95 (2): 420–442. Дои:10.1016/0375-9474(67)90510-6. ISSN 0375-9474.
- ^ К. Вейджманс (1991). Процесс ядерного деления. Бока-Ратон: CRC Press. ISBN 9780849354342.






























