WikiDer > Великая антипризма - Википедия

Grand antiprism - Wikipedia

Великая антипризма
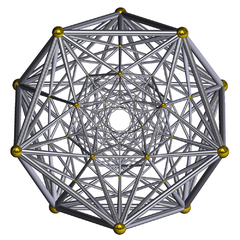(Диаграмма Шлегеля каркас)
Тип	Равномерный 4-многогранник
Единый индекс	47
Клетки	100+200 (3.3.3) 20 (3.3.3.5)
Лица	20 {5} 700 {3}
Края	500
Вершины	100
Фигура вершины	Sphenocorona
Группа симметрии	Ионно уменьшенная группа Кокстера [[10,2⁺, 10]] порядка 400
Символ Шлефли	с {5}. с {5} (расширенный)
Характеристики	выпуклый
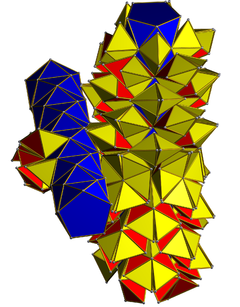А сеть показаны два непересекающихся кольца из 10 антипризм. 200 тетраэдров (желтые) находятся в торцевом контакте с антипризмами, а 100 тетраэдров (красные) контактируют только с другими тетраэдрами.

В геометрия, то великая антипризма или же пятиугольный двойной антипризмоид это равномерный 4-многогранник (4-х мерная униформа многогранник) ограничено 320 клетки: 20 пятиугольные антипризмы, и 300 тетраэдры. Это аномально, не уайтоффианец однородный 4-многогранник, открытый в 1965 г. Конвей и Парень.^[1]^[2] Топологически при высшей симметрии пятиугольные антипризмы имеют D_5d симметрии и есть два типа тетраэдров, один с S₄ симметрия и один с C_s симметрия.

Альтернативные имена

Пятиугольный двойной антипризмоид Норман В. Джонсон
Гэп (Джонатан Бауэрс: за грандиозную антипризму)^[3]

Структура

20 уложенных друг на друга пятиугольных антипризм образуют два непересекающихся кольца по 10 антипризм в каждом. Антипризмы в каждом кольце соединены друг с другом своими пятиугольными гранями. Два кольца взаимно перпендикулярны по структуре, подобной кольцу. дуопризма.

300 тетраэдров соединяют два кольца друг с другом и расположены в двумерном расположении, топологически эквивалентном кольцу. 2-тор и гребень дуоцилиндра. Их можно разделить на три группы. 100 сопрягаются по граням с одним кольцом, 100 сопрягаются по граням с другим кольцом, а 100 сопрягаются по центру точно в средней точке дуоцилиндра и сопрягаются по краям с обоими кольцами. Этот последний набор образует плоский тор и может быть «развернут» в плоский квадратный массив 10 × 10 тетраэдров, которые пересекаются только своими краями и вершинами. См. Рисунок ниже.

100 тетраэдров в массиве 10 × 10, образующем границу тора Клиффорда в 600-ячейке и большой антипризме.

Кроме того, 300 тетраэдров можно разбить на 10 непересекающихся Спирали Бурдейка – Кокстера из 30 ячеек, которые закрываются одна на другую. Две пятиугольные антипризматические трубки плюс 10 спиралей BC образуют нерегулярную дискретную Расслоение Хопфа великой антипризмы, которую Хопф сопоставляет с гранями пятиугольной антипризмы. Две трубки соответствуют двум пятиугольным граням, а спирали 10 г. до н.э. соответствуют 10 треугольным граням.

Структура большой антипризмы аналогична структуре трехмерной антипризмы. Однако большая антипризма - единственный выпуклый однородный аналог антипризмы в 4-х измерениях (хотя 16 ячеек можно рассматривать как обычный аналог двуугольный антипризма). Единственный невыпуклый однородный 4-мерный аналог антипризмы использует пентаграмматические скрещенные антипризмы вместо пятиугольной антипризмы и называется пентаграмматический двойной антипризмоид.

Фигура вершины

Вершинная фигура большой антипризмы - это сфенокорона или же правильный икосаэдр в разрезе: правильный икосаэдр с удаленными двумя соседними вершинами. На их месте 8 треугольников заменены парой трапеций, длины ребер φ, 1, 1, 1 (где φ - Золотое сечение), соединенные по ребру длины φ, чтобы получить тетрадекаэдр чьи лица 2 трапеции и 12 оставшихся равносторонние треугольники.

12 (3.3.3)	2 (3.3.3.5)	Рассеченный правильный икосаэдр

Строительство

Регулярный 600 ячеек могут быть разложены по симметрии большой антипризмы, причем каждая из 20 синих пятиугольных антипризм разделена на 15 правильных тетраэдров.

Большую антипризму можно построить убывающий 600-элементный: вычитание 20 пирамид, основания которых являются трехмерными пятиугольными антипризмами. И наоборот, два кольца пятиугольных антипризм в большой антипризме могут быть триангулированы 10 тетраэдрами, соединенными с треугольными гранями каждой антипризмы, и окружностью из 5 тетраэдров между каждой парой антипризм, соединяющей 10 тетраэдров каждой, давая 150 тетраэдров на звенеть. Они в сочетании с 300 тетраэдрами, которые соединяют два кольца вместе, дают 600 тетраэдров из 600 ячеек.

Это уменьшение может быть реализовано путем удаления двух колец по 10 вершин из 600-ячеек, каждое из которых лежит во взаимно ортогональных плоскостях. Каждое кольцо удаленных вершин создает стопку пятиугольных антипризм на выпуклый корпус. Это отношение аналогично тому, как пятиугольная антипризма можно построить из икосаэдр удалив две противоположные вершины, тем самым удалив 5 треугольников из противоположных «полюсов» икосаэдра, оставив 10 экваториальных треугольников и два пятиугольника вверху и внизу.

(The курносый 24-элементный также может быть построен путем другого уменьшения 600-ячеек, удалив 24 икосаэдрические пирамиды. Эквивалентно это может быть реализовано как взятие выпуклой оболочки вершин, оставшихся после 24 вершин, соответствующей таковым у вписанного 24-элементный, удалены из 600-ячеек.)

В качестве альтернативы он также может быть построен из десятиугольный дитетраголтриат (выпуклая оболочка двух перпендикулярных неоднородных 10-10 дуопризм где отношение двух декагонов находится в Золотое сечение) через чередование процесс. В десятиугольные призмы чередоваться в пятиугольные антипризмы, то прямоугольные трапеции чередоваться в тетраэдры с двумя новыми регулярными тетраэдры (представляет собой непореалмический треугольная бипирамида), созданного в удаленных вершинах. Это единственное однородное решение для p-угольных двойных антипризмоидов наряду с его конъюгатом, пентаграмматическим двойным антипризмоидом из декаграмматического дитетраголтриата.

Ортогональные проекции
600 ячеек	Великая антипризма
ЧАС₄ Самолет Кокстера

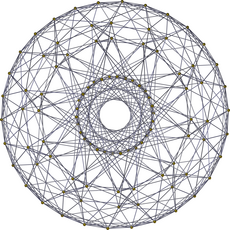20-угольный

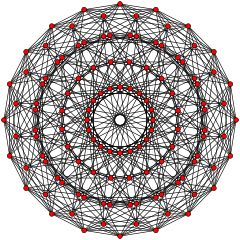ЧАС₃ Плоскость Кокстера (небольшое смещение)

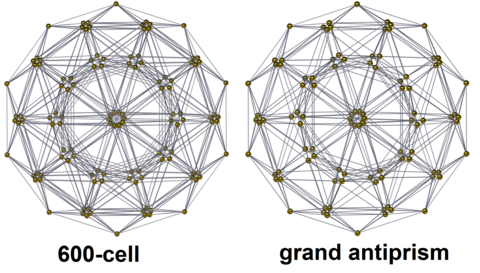Прогнозы

Это две перспективные проекции, проецирующие многогранник в гиперсфера, и применяя стереографическая проекция в 3-х пространстве.

Каркас, вид на одну из пятиугольных антипризматических колонн.	с прозрачными треугольными гранями
Ортографическая проекция Сосредоточено на гиперплоскость антипризмы в одном из двух колец.	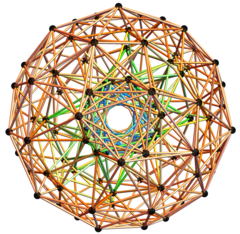3D орфографическая проекция 100 из 120 вершин с 600 ячейками и 500 ребер {488 из 1/2 (3-Sqrt [5]) и 12 из 2 / (3 + Sqrt [5])}.

Смотрите также

Примечания

^ J.H. Конвей и M.J.T. Парень: Четырехмерные архимедовы многогранники, Proceedings of the Colloquium on Convexity in Copenhagen, page 38 and 39, 1965. (Майкл Гай - сын Ричард К. Гай)
^ Конвей, 2008, с.402-403 Великая Антипризма.
^ Клитцинг, Ричард. «4D выпуклая полихора Большая антипризма».

внешняя ссылка

Во чреве Великой Антипризмы (средний раздел, описывающий аналогию с икосаэдром и пятиугольной антипризмой)

v т е Фундаментальный выпуклый обычный и однородные многогранники в размерах 2–10
Семья	А_п	B_п	я₂(п) / D_п	E₆ / E₇ / E₈ / F₄ / грамм₂	ЧАС_п
Правильный многоугольник	Треугольник	Квадрат	п-угольник	Шестиугольник	Пентагон
Равномерный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный 4-многогранник	5-элементный	16 ячеек • Тессеракт	Demitesseract	24-элементный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-полукруглый
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-полукуб	1₂₂ • 2₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-полукруглый	1₃₂ • 2₃₁ • 3₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-полукруглый	1₄₂ • 2₄₁ • 4₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-полукруглый
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-полукуб
Униформа п-многогранник	п-симплекс	п-ортоплекс • п-куб	п-полукуб	1_k2 • 2_k1 • k₂₁	п-пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений

[1] J.H. Конвей и M.J.T. Парень: Четырехмерные архимедовы многогранники, Proceedings of the Colloquium on Convexity in Copenhagen, page 38 and 39, 1965. (Майкл Гай - сын Ричард К. Гай)

[2] Конвей, 2008, с.402-403 Великая Антипризма.

[3] Клитцинг, Ричард. «4D выпуклая полихора Большая антипризма».

[1]

[2]

[3]

Navigation