WikiDer > Многогранник H4
 120 ячеек |  600 ячеек |
В 4-х мерном геометрия, всего 15 однородные многогранники с H4 симметрия. Два из них, 120 ячеек и 600 ячеек, находятся обычный.
Визуализации
Каждый может быть визуализирован как симметричный орфографические проекции в Самолеты Кокстера H4 Группа Кокстера и другие подгруппы.
Трехмерное изображение нарисовано как Диаграмма Шлегеля выступы, центрированные на ячейке в поз. 3, с последовательной ориентацией, а 5 ячеек в позиции 0 показаны сплошными.
| # | Имя | Самолет Кокстера прогнозы | Диаграммы Шлегеля | Сеть | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| F4 [12] | [20] | H4 [30] | H3 [10] | A3 [4] | A2 [3] | Додекаэдр по центру | Тетраэдр по центру | |||
| 1 | 120 ячеек {5,3,3} |  |  |  |  |  |  |  |  | |
| 2 | выпрямленный 120-элементный г {5,3,3} |  |  |  |  |  |  |  |  | |
| 3 | выпрямленный 600-элементный г {3,3,5} |  |  |  |  | 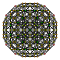 | 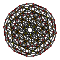 |  |  | |
| 4 | 600 ячеек {3,3,5} |  |  |  | 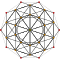 |  | 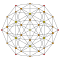 |  |  |  |
| 5 | усеченный 120-элементный т {5,3,3} |  |  |  |  |  |  |  |  | |
| 6 | скошенный 120-элементный рр {5,3,3} |  |  |  |  |  | ||||
| 7 | беглый 120-клеточный (также беглый 600-клеточный) т0,3{5,3,3} |  |  |  |  |  | ||||
| 8 | усеченный по битам 120-элементный (также усеченный битами, 600 ячеек) т1,2{5,3,3} |  |  |  |  |  | ||||
| 9 | скошенный 600-ячеечный т0,2{3,3,5} |  |  |  |  |  | 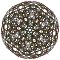 |  |  | |
| 10 | усеченный 600-ячеечный т {3,3,5} |  |  |  | 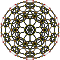 |  |  |  |  | |
| 11 | усеченный 120-элементный tr {5,3,3} |  |  |  |  |  | ||||
| 12 | усеченный 120-элементный т0,1,3{5,3,3} |  |  |  |  |  | ||||
| 13 | усеченный 600-ячеечный т0,1,3{3,3,4} |  |  |  |  |  | ||||
| 14 | усеченный 600-ячеечный tr {3,3,5} |  |  |  |  |  | ||||
| 15 | усеченная 120-ячеечная (также полностью усеченный 600-ячеечный) т0,1,2,3{5,3,3} |  |  |  |  |  | ||||
| # | Имя | Самолет Кокстера прогнозы | Диаграммы Шлегеля | Сеть | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| F4 [12] | [20] | H4 [30] | H3 [10] | A3 [4] | A2 [3] | Додекаэдр по центру | Тетраэдр по центру | |||
| 16 | 20-элементный 600-элементный (великая антипризма) | 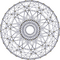 |  |  | ||||||
| 17 | 24 уменьшенных 600-ячеек (курносый 24-элементный) |  |  | 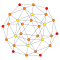 |  | |||||
| 18 Неоднородный | Bi-24-уменьшенный 600-элементный |  |  |  | ||||||
| 19 Неоднородный | 120-элементный выпрямленный 600-элементный |  | ||||||||
Координаты
Координаты равномерных многогранников из H4 семья сложная. Регулярные можно выразить через Золотое сечение φ = (1 + √5) / 2 и σ = (3√5 + 1) / 2. Кокстер выразил их как 5-мерные координаты.[1]
| п | 120 ячеек | 600 ячеек |
|---|---|---|
| 4D | 600 вершин 120-ячейки включают все перестановки из:[2]
и все даже перестановки из
| Вершины 600-ячейки с центром в начале координат 4-пространства с ребрами длины 1 / φ (где φ = (1+√5) / 2 - это Золотое сечение), можно задать так: 16 вершин вида:[3]
и 8 вершин, полученных из
Остальные 96 вершин получаются взятием даже перестановки из
|
| 5D | Перестановка с нулевой суммой:
| Перестановка с нулевой суммой:
|
Рекомендации
- J.H. Конвей и M.J.T. Парень: Четырехмерные архимедовы многогранники, Труды коллоквиума по выпуклости в Копенгагене, стр. 38 и 39, 1965 г.
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26)
- H.S.M. Coxeter:
- H.S.M. Кокстер, Правильные многогранники, 3-е издание, Довер, Нью-Йорк, 1973
- Калейдоскопы: Избранные произведения Х.С.М. Coxeter, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 Wiley :: Калейдоскопы: избранные произведения Х.С.М. Coxeter
- (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Документ 23) Х.С.М. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) 559-591]
- (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. Диссертация, Университет Торонто, 1966 г.
Примечания
- ^ Кокстер, Правильные и полурегулярные многогранники II, Четырехмерные многогранники ', с.296-298
- ^ Вайсштейн, Эрик В. «120-элементный». MathWorld.
- ^ Вайсштейн, Эрик В. «600 ячеек». MathWorld.
внешняя ссылка
- Клитцинг, Ричард. "4D равномерные 4-многогранники".
- Равномерные выпуклые многогранники в четырех измерениях:, Марко Мёллер (на немецком)
- Мёллер, Марко (2004). Vierdimensionale Archimedische Polytope (PDF) (Докторская диссертация) (на немецком языке). Гамбургский университет.
- Равномерные многогранники в четырех измерениях, Георгий Ольшевский.
- Выпуклая однородная полихора на основе 120/600 клеток, Георгий Ольшевский.
- Равномерные многогранники H4 с координатами: {5,3,3}, {3,3,5}, г {5,3,3},г {3,3,5}, т {3,3,5}, т {5,3,3}, рр {3,3,5}, рр {5,3,3}, tr {3,3,5}, tr {5,3,3}, 2т {5,3,3}, t03 {5,3,3}, t013 {3,3,5}, t013 {5,3,3}, t0123 {5,3,3}, великая антипризма