WikiDer > Генерация сетки

Mesh generation
Конечно-элементная сетка четырехугольников криволинейной области.

Генерация сетки это практика создания сетка- разбиение непрерывного геометрического пространства на дискретные геометрические и топологические ячейки, часто образующие симплициальный комплексОбычно ячейки разделяют геометрическую входную область. Ячейки сетки используются как дискретные локальные аппроксимации большей области. Сети создаются с помощью компьютерных алгоритмов, часто под руководством человека через GUI , в зависимости от сложности домена и желаемого типа сетки. Цель состоит в том, чтобы создать сетку, которая точно отражает геометрию входной области, с высококачественными (правильными) ячейками и без такого количества ячеек, чтобы делать последующие Сетка также должна быть мелкой (иметь мелкие элементы) в областях, важных для последующих расчетов.

Сетки используются для рендеринг к экрану компьютера и для физическое моделирование Такие как анализ методом конечных элементов или же вычислительная гидродинамика. Сетки состоят из простых ячеек, таких как треугольники, потому что, например, мы знаем, как выполнять такие операции, как вычисления методом конечных элементов (инженерия) или трассировка лучей (компьютерная графика) на треугольниках, но мы не знаем, как выполнять эти операции непосредственно на сложных пространствах. и формы, такие как проезжий мост. Мы можем смоделировать прочность моста или нарисовать его на экране компьютера, выполнив вычисления для каждого треугольника и вычислив взаимодействия между треугольниками.

Основное различие между структурированными и неструктурированными сетками. В структурированной сетке сетка представляет собой обычную решетку, такую ​​как массив, с подразумеваемой связностью между элементами. В неструктурированной сетке элементы могут быть соединены друг с другом по нерегулярной схеме, и могут быть захвачены более сложные области. Эта страница в основном посвящена неструктурированным сеткам. Хотя сетка может быть триангуляция, процесс создания сетки отличается от триангуляция набора точек в этом построении сетки есть возможность добавлять вершины, которых нет во входных данных. «Фацетирование» (триангуляция) CAD модели для рисования имеют такую ​​же свободу добавления вершин, но цель состоит в том, чтобы точно представить форму, используя как можно меньше треугольников, а форма отдельных треугольников не важна. При визуализации текстур и реалистичных условий освещения компьютерной графикой вместо этого используются сетки.

Многие программы для создания сеток связаны с Система CAD определение его ввода и программное обеспечение моделирования для его вывода. Входные данные могут сильно различаться, но общие формы Твердотельное моделирование, Геометрическое моделирование, NURBS, B-rep, STL или облако точек.

Терминология

Условия "генерация сетки," "генерация сетки," "сетка" " и "сетка«часто используются как взаимозаменяемые, хотя, строго говоря, последние два являются более широкими и включают улучшение сетки: изменение сетки с целью увеличения скорости или точности численных расчетов, которые будут выполняться над ней. компьютерная графика рендеринг и математика, сетку иногда называют мозаика.

Грани сетки (ячейки, объекты) имеют разные имена в зависимости от их размера и контекста, в котором будет использоваться сетка. В конечных элементах элементы сетки с наибольшей размерностью называются «элементами», «ребра» - 1D, а «узлы» - 0D. Если элементы являются трехмерными, то двумерные объекты являются «гранями». В вычислительной геометрии 0D-точки называются вершинами. Тетраэдры часто сокращенно называют «тетраэдрами»; треугольники - это «трис», четырехугольники - «четырехугольники», а шестигранники (топологические кубы) - «шестиугольники».

Методы

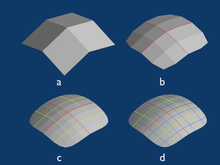
Подразделение Catmull-Clark поверхности
Сетка, созданная из неявная поверхность

Многие техники построения сетки построены на принципах Триангуляция Делоневместе с правилами добавления вершин, такими как Алгоритм РуппертаОтличительной особенностью является то, что сначала формируется грубая сетка всего пространства, затем добавляются вершины и треугольники. передовые алгоритмы фронта начните с границы домена и добавляйте элементы постепенно, заполняя интерьер. Гибридные методы делают и то, и другое. Специальный класс передовых техник создает тонкие пограничные слои элементов для потока жидкости.При построении структурированной сетки вся сетка является решетчатый граф, например, регулярная сетка из квадратов. Создание структурированной сетки за регулярные сетки представляет собой целое поле, с применением математических методов для обеспечения того, чтобы линии сетки высокого полиномиального порядка плавно и точно следовали пространству решения. При блочно-структурированной сетке область делится на большие подобласти, каждая из которых представляет собой структурированную сетку. прямые методы начинаются с сетки с блочной структурой, а затем перемещают сетку в соответствии с входными данными; видеть Автоматическое создание шестигранной сетки на основе поликуб. Другой прямой метод - разрезать структурированные ячейки по границе домена; видеть лепить на основе Маршевые кубики.

Некоторые типы сеток создать намного сложнее, чем другие. Симплициальные сетки обычно проще кубических. Важной категорией является создание шестигранной сетки, соответствующей фиксированной четырехугольной поверхностной сетке; Подрайон исследований изучает существование и создание сеток определенных небольших конфигураций, таких как тетрагональный трапецииэдр. Из-за сложности этой проблемы, существование комбинаторных шестигранных сеток изучалось отдельно от проблемы генерации хороших геометрических реализаций. В то время как известные алгоритмы генерируют симплициальные сетки с гарантированным минимальным качеством, такие гарантии редки для кубических сеток, и многие популярные реализации генерируют перевернутые (вывернутые наизнанку) гексы из некоторых входных данных.

Сетки часто создаются последовательно на рабочих станциях, даже если последующие расчеты по сетке будут выполняться в параллельно на суперкомпьютерах. Это связано как с ограничением, заключающимся в том, что большинство генераторов сеток являются интерактивными, так и потому, что время выполнения генерации сетки обычно незначительно по сравнению со временем решателя. Однако, если сетка слишком велика, чтобы поместиться в памяти одной последовательной машины, или сетка должна быть изменена (адаптирована) во время моделирования, сетка выполняется параллельно.

Типы сеток

Смотрите также Виды сетки.

Топология ячейки

Обычно клетки многоугольный или же многогранник и сформировать сетка Это разделяет область. Важные классы двумерных элементов включают треугольники (симплексы) и четырехугольники (топологические квадраты). В трехмерных ячейках наиболее распространенными ячейками являются тетраэдры (симплексы) и гексаэдры (топологические кубы).Симплициальный сетки могут быть любого размера и включать в себя треугольники (2D) и тетраэдры (3D) в качестве важных примеров.Кубические сетки - это категория пан-измерения, которая включает в себя четырехугольники (2D) и шестиугольники (3D). В 3D 4-сторонние пирамиды и 3-сторонние призмы появляются в конформных сетках смешанного типа ячеек.

Размер ячейки

Сетка встроена в геометрическое пространство, которое обычно два или же трехмерный, хотя иногда измерение увеличивается на единицу, добавляя измерение времени. Сетки более высокой размерности используются в нишевых контекстах. Одномерные сетки тоже полезны. Важная категория - это поверхностные сетки, которые представляют собой 2D-сетки, встроенные в 3D для представления криволинейной поверхности.

Двойственность

Двойные графики играют несколько ролей в построении сетки. Можно сделать многогранник Диаграмма Вороного сетка путем дуализации Триангуляция Делоне симплициальная сетка. Можно создать кубическую сетку, создав расположение поверхностей и дуализируя граф пересечений; видеть пространственный твист континуум. Иногда и основная сетка, и двойная сетка используются в одной и той же симуляции; видеть Звездный оператор Ходжа. Это связано с физикой, включающей расхождение и локон (математика) операторы, такие как поток & завихренность или же электричество и магнетизм, где одна переменная естественным образом живет на первичных гранях, а ее двойник - на двойных гранях.

Тип сетки по использованию

Трехмерные сетки созданы для анализ методом конечных элементов должен состоять из тетраэдры, пирамиды, призмы или же шестигранник. Те, которые использовались для метод конечных объемов может состоять из произвольных многогранники. Те, которые использовались для методы конечных разностей состоят из кусочно-структурированных массивов шестигранник известны как многоблочные структурированные сетки. Четырехсторонние пирамиды используются для конформного соединения шестиугольников с тетами. Трехсторонние призмы используются для граничных слоев, соответствующих решетчатой ​​сетке дальней внутренней части объекта.

Поверхностные сетки полезны в компьютерной графике, где поверхности объектов отражают свет (также подповерхностное рассеяние) и полная трехмерная сетка не требуется. Поверхностные сетки также используются для моделирования тонких объектов, таких как листовой металл, в автомобилестроении и экстерьеров зданий в архитектуре. Кубические сетки большой (например, 17) размерности распространены в астрофизике и теория струн.

Математическое определение и варианты

Каково точное определение сетка? Не существует общепринятого математического описания, применимого во всех контекстах. Однако некоторые математические объекты явно являются сетками: симплициальный комплекс представляет собой сетку, состоящую из симплексов. Большинство полиэдральных (например, кубических) сеток конформный это означает, что они имеют клеточную структуру CW комплекс, обобщение симплициальный комплекс. Сетка не обязательно должна быть симплициальной, потому что произвольное подмножество узлов ячейки не обязательно является ячейкой: например, три узла четырехугольника не определяют ячейку. Однако две ячейки пересекаются в ячейках: например, у четырехугольника нет узла внутри. На пересечении двух ячеек может быть несколько ячеек: например, два квадрата могут иметь два общих ребра. Пересечение более чем одной ячейки иногда запрещено и редко желательно; цель некоторых методов улучшения сетки (например, подушечки) состоит в том, чтобы удалить эти конфигурации. В некоторых контекстах проводится различие между топологической сеткой и геометрической сеткой, встраивание которой удовлетворяет определенным критериям качества.

Важные варианты сеток, которые не являются комплексами CW, включают неконформные сетки, где ячейки не встречаются строго лицом к лицу, но ячейки, тем не менее, разделяют домен. Примером этого является октодерево, где грань элемента может быть разделена гранями соседних элементов. Такие сетки полезны для моделирования на основе потоков. В сетках с перекрытием есть несколько конформных сеток, которые геометрически перекрываются и не разделяют область; см., например, Переполнение, решатель OVERset grid FLOW. Так называемые бессеточные или бессеточные методы часто используют некоторую сетчатую дискретизацию области и имеют базовые функции с поддержкой перекрытия. Иногда локальная сетка создается около каждой точки степени свободы моделирования, и эти сетки могут перекрываться и быть неконформными друг другу.

Элементы высокого порядка

Во многих сетках используются линейные элементы, при этом отображение абстрактного элемента в реализованный является линейным, а края сетки - прямыми сегментами. Часто встречаются полиномиальные отображения более высокого порядка, особенно квадратичные. Основная цель для элементов более высокого порядка состоит в том, чтобы более точно представить границу домена, хотя они имеют преимущество в точности и внутри сетки. Одним из мотивов создания кубических сеток является то, что линейные кубические элементы имеют некоторые из тех же численных преимуществ. как квадратичные симплициальные элементы. изогеометрический анализ При моделировании ячейки сетки, содержащие границу домена, используют представление САПР напрямую вместо линейного или полиномиального приближения.

Улучшение сетки

Улучшение сетки включает изменение ее дискретной связности, непрерывного геометрического положения ее ячеек или того и другого. Для дискретных изменений, для симплициальных элементов меняют местами края и вставляют / удаляют узлы. Те же операции выполняются и для кубических (четырехугольных / шестнадцатеричных) сеток, хотя существует меньше возможных операций, а локальные изменения имеют глобальные последствия. Например, для гексаэдрической сетки слияние двух узлов создает ячейки, которые не являются гексагонами, но если диагонально противоположные узлы на четырехугольнике объединяются, и это распространяется на сжатие всего соединенного гранями столбца гексов, тогда все оставшиеся ячейки все равно будут гексы. В адаптивное уточнение сетки, элементы разделяются (h-уточнение) в областях, где вычисляемая функция имеет высокий градиент. Сетки также огрубляются, удаляя элементы для повышения эффективности. В многосеточный метод делает что-то похожее на уточнение и укрупнение, чтобы ускорить численное решение, но без фактического изменения сетки.

Для непрерывных изменений узлы перемещаются или грани более высоких измерений перемещаются путем изменения полиномиального порядка элементов. Перемещение узлов для улучшения качества называется «сглаживанием» или «r-уточнением», а увеличение порядка элементов называется «p-уточнением». Узлы также перемещаются при моделировании, когда форма объектов меняется со временем. Это ухудшает форму элементов. Если объект достаточно деформируется, весь объект заменяется сеткой, и текущее решение отображается из старой сетки в новую.

Практикующие

Эта область является междисциплинарной, и ее вклад можно найти в математика, Информатика, и инженерное дело. Исследования и разработки создания сетки отличаются одинаковым вниманием к дискретной и непрерывной математике и вычислениям, как и в случае с вычислительная геометрия, но в отличие от теория графов (дискретный) и числовой анализ (непрерывный). Создание сетки обманчиво сложно: людям легко увидеть, как создать сетку из заданного объекта, но сложно запрограммировать компьютер, чтобы априори принимать правильные решения для произвольного ввода. В природе и объектах, созданных руками человека, существует бесконечное разнообразие геометрии. Многие исследователи создания сеток были первыми пользователями сеток. Генерация сеток продолжает получать широкое внимание, поддержку и финансирование, потому что человеческое время для создания сетки затмевает время, необходимое для настройки и выполнения вычислений после завершения сетки. Так было всегда с момента изобретения численного моделирования и компьютерной графики, потому что по мере совершенствования компьютерного оборудования и простого программного обеспечения для решения уравнений люди были привлечены к более крупным и более сложным геометрическим моделям в стремлении к большей точности, научному пониманию и художественное выражение.

Общественная деятельность

Литература по созданию сетки список веб-сайтов

Журналы

Исследования построения сетки публикуются в различных журналах. Это соответствует междисциплинарному характеру исследований, необходимых для достижения прогресса, а также широкому спектру приложений, в которых используются сетки. Ежегодно в 20 журналах появляется около 150 взаимосвязанных публикаций, причем в одном журнале появляется не более 20 публикаций. Нет журнала, основная тема которого связана с сеткой. Журналы, которые публикуют не менее 10 статей в год, находятся в смелый.

Конференции

Конференции, основная тема которых - объединение, находятся в смелый.

Конференции, семинары, летние школы список веб-сайтов

Мастерские

Семинары, основная тема которых - создание сетки, находятся в смелый.

  • Конференция по геометрии: теория и приложения CGTA
  • Европейский семинар по вычислительной геометрии EuroCG
  • Осенний семинар по вычислительной геометрии
  • Конечные элементы в жидкостях FEF
  • Симпозиум MeshTrends (в другие годы WCCM или USNCCM)
  • Методы многогранных элементов в математике и инженерии
  • Мастерская тетраэдра

Ресурсы

Генераторы сеток

Во многих описаниях коммерческих продуктов делается упор на моделирование, а не на технологию построения сеток, обеспечивающую моделирование.

Генераторы многодоменных секционированных сеток

Эти инструменты генерируют разделенные сетки, необходимые для моделирования методом конечных элементов из нескольких материалов.

  • MDM(Multiple Domain Meshing) автоматически и эффективно генерирует неструктурированные тетраэдрические и гексаэдрические сетки для композитного домена, состоящего из гетерогенных материалов.
  • QMDM (Качественная многодоменная сетка) создает высококачественные взаимно согласованные треугольные поверхностные сетки для нескольких доменов.
  • QMDMNG, (Качественная многодоменная сетка без зазоров), создает качественные сетки, каждая из которых представляет собой двумерное многообразие и без зазора между двумя соседними сетками.
  • SOFA_mesh_partitioning_tools генерирует разделенные тетраэдрические сетки для многоматериальных МКЭ на основе CGAL.

Статьи

Исследовательские группы и люди

Модели и сетки

Полезные модели (входные данные) и сетки (выходы) для сравнения алгоритмов построения сеток и сеток.

CAD модели

Механизмы моделирования, связанные с программным обеспечением для создания сеток, для представления геометрии домена.

Форматы файлов сетки

Общие (выходные) форматы файлов для описания сеток.

Mesio можно конвертировать между всеми вышеперечисленными форматами.

Визуализаторы сетки

Книги

Учебники

Смотрите также

Рекомендации

  • Эдельсбруннер, Герберт (2001), «Геометрия и топология для создания сетки», Обзоры прикладной механики, Издательство Кембриджского университета, 55 (1): B1 – B2, Bibcode:2002ApMRv..55B ... 1E, Дои:10.1115/1.1445302, ISBN 978-0-521-79309-4.
  • Фрей, Паскаль Жан; Джордж, Поль-Луи (2000), Создание сетки: приложение к конечным элементам, Наука Гермеса, ISBN 978-1-903398-00-5.
  • П. Смит и С. С. Шритаран (1988), «Теория генерации гармонических сеток» (PDF), Комплексные переменные, 10 (4): 359–369, Дои:10.1080/17476938808814314
  • С. С. Шритаран (1992), "Теория генерации гармонических решеток-II", Применимый анализ, 44 (1): 127–149, Дои:10.1080/00036819208840072
  • Томпсон, Дж. Ф.; Warsi, Z.U. A .; Мастин, К. В. (1985), Создание числовых сеток: основы и приложения, Северная Голландия, Эльзевир.
  • CGAL Библиотека алгоритмов вычислительной геометрии
  • Оден, Дж. Тинсли; Чо, Дж. Р. (1996), "Адаптивные hpq-методы конечных элементов иерархических моделей для пластинчатых и оболочечных структур", Компьютерные методы в прикладной механике и технике, 136 (3): 317–345, Bibcode:1996CMAME.136..317O, Дои:10.1016/0045-7825(95)00986-8
  • Стивен Дж. Оуэн (1998), Обзор технологии создания неструктурированной сетки, стр. 239–267
  • Шимада, Кендзи; Госсард, Дэвид К. (1995), Пузырьковая сетка: автоматическое построение треугольной сетки немножечной геометрии с помощью сферической упаковки, ACM, стр.409-419, Дои:10.1145/218013.218095, ISBN 0-89791-672-7
  • Ян Брандтс, Сергей Коротов, Михал Крижек: «Симплициальные разбиения с приложениями к методу конечных элементов», Монографии Springer по математике,ISBN 978-3030556761 (2020). url = "https://www.springer.com/gp/book/9783030556761"