WikiDer > Молекулярное моделирование

Позвоночник двугранные углы включены в молекулярную модель белок.

Моделирование ионной жидкости

Молекулярное моделирование охватывает все методы, теоретические и вычислительные, используемые для модель или имитировать поведение молекулы.^[1] Методы используются в областях вычислительная химия, дизайн лекарства, вычислительная биология и материаловедение изучать молекулярные системы, от небольших химических систем до больших биологических молекул и материальных сборок. Простейшие расчеты можно выполнить вручную, но для молекулярного моделирования любой системы разумного размера неизбежно требуются компьютеры. Общей чертой методов молекулярного моделирования является описание молекулярных систем на атомистическом уровне. Это может включать рассмотрение атомов как наименьшей индивидуальной единицы ( молекулярная механика подход), или явное моделирование протонов и нейтронов своими кварками, антикварками и глюонами и электронов своими фотонами (a квантовая химия подход).

Молекулярная механика

Молекулярная механика является одним из аспектов молекулярного моделирования, так как он предполагает использование классическая механика (Ньютоновская механика), чтобы описать физическую основу моделей. Молекулярные модели обычно описывают атомы (ядро и электроны вместе) как точечные заряды с соответствующей массой. Взаимодействия между соседними атомами описываются пружинными взаимодействиями (представляющими химические связи) и Силы Ван-дер-Ваальса. В Потенциал Леннарда-Джонса обычно используется для описания последнего. Электростатические взаимодействия рассчитываются на основе Закон Кулона. Атомам присваиваются координаты в декартовом пространстве или в внутренние координаты, а также могут быть назначены скорости в динамическом моделировании. Скорости атомов связаны с температурой системы, макроскопической величиной. Коллективное математическое выражение называется потенциальная функция и связан с внутренней энергией системы (U), термодинамической величиной, равной сумме потенциальной и кинетической энергий. Методы, которые минимизируют потенциальную энергию, называются методами минимизации энергии (например, крутой спуск и сопряженный градиент), а методы, моделирующие поведение системы с течением времени, называются молекулярная динамика.

${ displaystyle E = E _ { text {bond}} + E _ { text {angle}} + E _ { text {dihed}} + E _ { text {non-bonded}} ,}$

${ displaystyle E _ { text {non-bonded}} = E _ { text {electrostatic}} + E _ { text {van der Waals}} ,}$

Эта функция, называемая потенциальная функция, вычисляет потенциальную энергию молекулы как сумму энергетических членов, которые описывают отклонение длин связей, валентных углов и торсионных углов от равновесных значений, плюс члены для несвязанных пар атомов, описывающие ван-дер-ваальсовы и электростатические взаимодействия. Набор параметров, состоящий из длины равновесных связей, валентных углов, значений парциального заряда, силовых постоянных и параметров Ван-дер-Ваальса, в совокупности называется силовое поле. Различные реализации молекулярной механики используют разные математические выражения и разные параметры для потенциальная функция.^[2] Общие силовые поля, используемые сегодня, были разработаны с использованием химической теории, экспериментальных справочных данных и высокоуровневых квантовых расчетов. Метод, называемый минимизацией энергии, используется для нахождения положений нулевого градиента для всех атомов, другими словами, локального минимума энергии. Состояния с более низкой энергией более стабильны и обычно исследуются из-за их роли в химических и биологических процессах. А молекулярная динамика симуляция, с другой стороны, вычисляет поведение системы как функцию времени. Он включает в себя решение законов движения Ньютона, в основном второго закона, ${ Displaystyle mathbf {F} = м mathbf {а}}$. Интеграция законов движения Ньютона с использованием различных алгоритмов интеграции приводит к атомным траекториям в пространстве и времени. Сила, действующая на атом, определяется как отрицательный градиент функции потенциальной энергии. Метод минимизации энергии полезен для получения статической картины для сравнения состояний подобных систем, в то время как молекулярная динамика дает информацию о динамических процессах с внутренним учетом температурных эффектов.

Переменные

Молекулы можно моделировать либо в вакууме, либо в присутствии растворителя, такого как вода. Моделирование систем в вакууме называется газовая фаза моделирования, в то время как те, которые включают присутствие молекул растворителя, называются явный растворитель симуляции. В другом типе моделирования влияние растворителя оценивается с помощью эмпирического математического выражения; они называются неявная сольватация симуляции.

Координатные представления

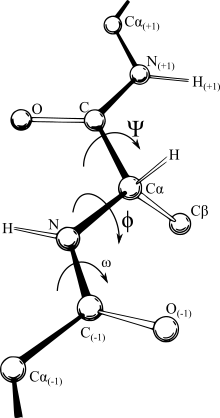
Большинство силовых полей зависят от расстояния, что делает наиболее удобное выражение для этих декартовых координат. Тем не менее, сравнительно жесткий характер связей, которые возникают между конкретными атомами и, по сути, определяет, что подразумевается под обозначением. молекула, сделайте внутреннюю систему координат наиболее логичным представлением. В некоторых областях представление IC (длина связи, угол между связями и угол закручивания связи, как показано на рисунке) называется Z-матрица или представление торсионного угла. К сожалению, непрерывные движения в декартовом пространстве часто требуют прерывистых угловых ветвей во внутренних координатах, что делает относительно трудным работу с силовыми полями во внутренних координатных представлениях, и, наоборот, простое смещение атома в декартовом пространстве может не быть прямой траекторией из-за к запретам взаимосвязанных облигаций. Таким образом, для программ оптимизации вычислений очень часто приходится переключаться между представлениями во время их итераций. Это может доминировать во времени вычисления самого потенциала, а в длинноцепочечных молекулах вносит совокупную численную неточность. Хотя все алгоритмы преобразования дают математически идентичные результаты, они различаются по скорости и числовой точности.^[3] В настоящее время самым быстрым и точным преобразованием кручения в декартово является метод системы отсчета естественного расширения (NERF).^[3]

Приложения

Методы молекулярного моделирования в настоящее время регулярно используются для исследования структуры, динамики, свойств поверхности и термодинамики неорганических, биологических и полимерных систем. Типы биологической активности, которые были исследованы с помощью молекулярного моделирования, включают: сворачивание белка, фермент катализ, стабильность белка, конформационные изменения, связанные с биомолекулярной функцией, и молекулярное распознавание белков, ДНК, и мембранные комплексы.^[4]

Смотрите также

Рекомендации

дальнейшее чтение