WikiDer > Силовое поле (химия) - Википедия
В контексте химия и молекулярное моделирование, а силовое поле это вычислительный метод, который используется для оценки сил между атомами внутри молекул, а также между молекулами. Точнее, силовое поле относится к функциональная форма и параметр наборы, используемые для расчета потенциальная энергия системы атомов или крупнозернистых частиц в молекулярная механика, молекулярная динамика, или же Монте-Карло симуляции. Параметры для выбранной энергетической функции могут быть получены из экспериментов в физика и химия, расчеты в квантовая механика, или оба. Силовые поля межатомные потенциалы и использовать ту же концепцию, что и силовые поля в классическая физика, с той разницей, что параметры силового поля в химии описывают энергетический ландшафт, из которого действующие силы на каждую частицу выводятся как градиент потенциальной энергии относительно координат частицы.[1]
Все-атом силовые поля обеспечивают параметры для каждого типа атома в системе, включая водород, пока объединенный атом межатомные потенциалы обрабатывают водород и углерод атомы в метильные группы и метиленовые мостики как единый центр взаимодействия.[2] Крупнозернистый потенциалы, которые часто используются при длительном моделировании макромолекулы Такие как белки, нуклеиновые кислоты, и многокомпонентные комплексы, жертвуют химическими деталями ради более высокой эффективности вычислений.[3]
Функциональная форма
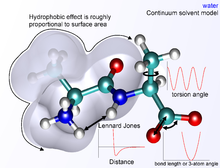
Базовая функциональная форма потенциальная энергия в молекулярная механика включает связанный термины для взаимодействия атомов, которые связаны между собой ковалентные связи, и небондовые (также называемые нековалентный) термины, описывающие дальние электростатический и силы Ван дер Ваальса. Конкретное разложение членов зависит от силового поля, но общий вид полной энергии в аддитивном силовом поле может быть записан как
где компоненты ковалентного и нековалентного вкладов даются следующими суммированиями:
Члены связи и угла обычно моделируются квадратичными энергетическими функциями, которые не допускают разрыва связи. Более реалистичное описание ковалентной связи при более высоком растяжении дает более дорогой Потенциал Морзе. Функциональная форма двугранной энергии меняется от одного силового поля к другому. Дополнительные, «неправильные крутильные» условия могут быть добавлены для обеспечения плоскостности ароматный кольца и другие сопряженные системы, и «перекрестные термины», которые описывают связь различных внутренних переменных, таких как углы и длины связей. Некоторые силовые поля также включают явные термины для водородные связи.
Несвязанные термины являются наиболее трудоемкими в вычислительном отношении. Популярный выбор - ограничить взаимодействия парными энергиями. Член Ван-дер-Ваальса обычно вычисляется с помощью Потенциал Леннарда-Джонса и электростатический член с Закон Кулона, хотя оба могут быть буферизированы или масштабированы с постоянным коэффициентом для учета электронных поляризуемость. Исследования с этим выражением энергии были сосредоточены на биомолекулах с 1970-х годов и были обобщены на соединения периодической таблицы в начале 2000-х годов, включая металлы, керамику, минералы и органические соединения.[4]
Растяжение связи
Поскольку облигации редко значительно отклоняются от своих справочных значений, в самых упрощенных подходах используется Закон Гука формула:
Где - силовая постоянная, длина связи и - значение длины связи между атомами и когда все остальные члены в силовом поле установлены на 0. Член часто называют длиной равновесной связи, что может вызвать путаницу. Равновесная длина связи - это значение, принятое в равновесии при 298 К с учетом всех других членов силового поля и кинетической энергии. Следовательно, часто на несколько процентов отличается от реальной длины связи в экспериментах при 298 К.[4]
Константа растяжения связи можно определить из экспериментальных Инфракрасный спектр, Раман спектр или высокий уровень квантово-механический расчеты. Постоянная определяет частоты колебаний в моделирование молекулярной динамики. Чем сильнее связь между атомами, тем выше значение силовой постоянной и тем выше волновое число (энергия) в ИК / Рамановском спектре. Спектр вибрации в соответствии с заданной силовой постоянной может быть вычислен из коротких траекторий MD (5 пс) с временными шагами ~ 1 фс, вычисления автокорреляционной функции скорости и ее преобразования Фурье.[5]
Хотя формула закона Гука обеспечивает разумный уровень точности при длинах связей, близких к равновесному расстоянию, она становится менее точной по мере удаления. Для лучшего моделирования кривой Морзе можно использовать кубические и более высокие степени.[2][6] Однако для большинства практических приложений эти различия незначительны, а неточности в предсказаниях длин связей составляют порядка одной тысячной ангстрема, что также является пределом надежности для обычных силовых полей. А Потенциал Морзе Вместо этого можно использовать для обеспечения разрыва связи и более высокой точности, даже если это менее эффективно для вычислений.
Электростатические взаимодействия
Электростатические взаимодействия представлены кулоновской энергией, которая использует атомные заряды представлять химическую связь в диапазоне от ковалентный к полярный ковалентный и ионная связь. Типичная формула - это Кулоновский закон:
Где это расстояние между двумя атомами и . Полная кулоновская энергия является суммированием по всем парным комбинациям атомов и обычно не включает 1, 2 связанных атома, 1, 3 связанных атома, а также 1, 4 связанных атома.[7][8][9]
Заряды атомов могут вносить основной вклад в потенциальную энергию, особенно для полярных молекул и ионных соединений, и имеют решающее значение для моделирования геометрии, энергии взаимодействия, а также реакционной способности. Присвоение атомных зарядов часто по-прежнему следует эмпирическим и ненадежным квантово-механическим протоколам, что часто приводит к нескольким 100% неопределенности относительно физически обоснованных значений в соответствии с экспериментальными дипольными моментами и теорией.[10][11][12] Были разработаны воспроизводимые атомные заряды для силовых полей на основе экспериментальных данных для плотности деформации электронов, внутренних дипольных моментов и расширенной модели Борна.[12][4] Погрешности <10%, или ± 0,1e, обеспечивают согласованное представление химической связи и до 100 раз более высокую точность вычисленных структур и энергий наряду с физической интерпретацией других параметров в силовом поле.
Параметризация
В дополнение к функциональной форме потенциалов силовые поля определяют набор параметров для различных типов атомов, химических связей, двугранных углов, внеплоскостных взаимодействий, не связанных взаимодействий и возможных других терминов.[4] Многие наборы параметров являются эмпирическими, а некоторые силовые поля используют обширные подгоночные термины, которые трудно дать физическую интерпретацию.[13] Типы атомов определены для разных элементов, а также для одних и тех же элементов в достаточно разных химических средах. Например, кислород атомы в воды и атомы кислорода в карбонил функциональная группа классифицируются как разные типы силовых полей.[14] Типичные наборы параметров силового поля включают значения для атомная масса, атомный заряд, Параметры Леннарда-Джонса для каждого типа атомов, а также равновесные значения длина облигаций, валентные углы, и двугранные углы.[15] Связанные термины относятся к парам, тройкам и четверкам связанных атомов и включают значения эффективных жесткость пружины для каждого потенциала. Большинство текущих параметров силовых полей используют фиксированная оплата модель, в которой каждому атому приписывается одно значение для атомного обвинять это не зависит от местных электростатический среда.[12][16]
Параметризация силового поля для моделирования с максимальной точностью и переносимостью, например, IFF, осуществляется в соответствии с четко определенным протоколом.[4] Рабочий процесс может включать (1) получение рентгеновской кристаллической структуры или химической формулы, (2) определение типов атомов, (3) получение атомных зарядов, (4) задание начальных параметров Леннарда-Джонса и связанных параметров, (5) вычислительные испытания плотность и геометрия относительно экспериментальных справочных данных, (6) расчетные испытания энергетических свойств (поверхностная энергия,[17] энергия гидратации[18]) относительно экспериментальных справочных данных, (7) вторичная проверка и уточнение (термические, механические и диффузионные свойства).[19] Основные итерационные циклы происходят между шагами (5) и (4), а также между (6) и (4) / (3). Химическая интерпретация параметров и надежные экспериментальные справочные данные играют решающую роль.
Параметры для молекулярного моделирования биологических макромолекулы Такие как белки, ДНК, и РНК часто выводились из наблюдений за небольшими Органические молекулы, которые более доступны для экспериментальных исследований и квантовых расчетов. Таким образом, возникает множество проблем, таких как (1) ненадежные атомные заряды из квантовых вычислений могут повлиять на все вычисленные свойства и внутреннюю согласованность, (2) данные, полученные из квантовой механики для молекул в газовой фазе, могут быть неприменимы для моделирования в конденсированной фаза, (3) использование данных для малых молекул и применение к более крупным полимерным структурам связано с неопределенностью, (4) несходные экспериментальные данные с вариациями точности и эталонных состояний (например, температуры) могут вызывать отклонения. В результате сообщалось о расходящихся параметрах силового поля для биологических молекул. Справочные экспериментальные данные включали, например, энтальпия из испарение (OPLS), энтальпия из сублимация, дипольные моменты, и различные спектроскопические параметры.[20][6][14] Несоответствия можно преодолеть путем интерпретации всех параметров силового поля и выбора постоянного эталонного состояния, например, комнатной температуры и атмосферного давления.[4]
Некоторые силовые поля также включают отсутствие четкого химического обоснования, протокола параметризации, неполную проверку ключевых свойств (структур и энергий), отсутствие интерпретации параметров и обсуждение неопределенностей.[21] В этих случаях сообщалось о больших случайных отклонениях вычисленных свойств.
Методы
Некоторые силовые поля включают явные модели для поляризуемость, где на эффективный заряд частицы могут влиять электростатические взаимодействия с ее соседями. Распространены модели ядро-оболочка, которые состоят из положительно заряженной основной частицы, представляющей поляризуемый атом, и отрицательно заряженной частицы, прикрепленной к сердцевинному атому посредством пружинной гармонический осциллятор потенциал.[22][23][24] Недавние примеры включают поляризуемые модели с виртуальными электронами, которые воспроизводят заряды изображения в металлах.[25] поляризуемые биомолекулярные силовые поля.[26] При добавлении таких степеней свободы для поляризуемости интерпретация параметров становится более сложной и увеличивает риск в отношении произвольных параметров соответствия и снижения совместимости. Вычислительные затраты увеличиваются из-за необходимости многократно вычислять локальное электростатическое поле.
Поляризуемые модели работают хорошо, когда они фиксируют основные химические свойства, а суммарный атомный заряд является относительно точным (в пределах ± 10%).[4][27] В последнее время такие модели ошибочно называют «потенциалами осциллятора Друде».[28] Подходящим термином для этих моделей является «модели осциллятора Лоренца», поскольку Лоренц[29] скорее, чем Друде[30] предложил некоторую форму прикрепления электронов к ядрам.[25] Модели друде предполагают неограниченное движение электронов, например, свободный электронный газ в металлах.[30]
Параметризация
Исторически использовалось много подходов к параметризации силового поля. Многочисленные классические силовые поля основывались на относительно непрозрачных протоколах параметризации, например, с использованием приближенных квантово-механических расчетов, часто в газовой фазе, с ожиданием некоторой корреляции со свойствами конденсированной фазы и эмпирических модификаций потенциалов для соответствия экспериментальным наблюдаемым.[31][32][33] Протоколы могут быть невоспроизводимыми, и полуавтоматизация часто играет роль для генерации параметров, оптимизации для быстрой генерации параметров и широкого охвата, а не для химической согласованности, интерпретируемости, надежности и устойчивости.
Аналогичные, даже более автоматизированные инструменты стали доступны недавно для параметризации новых силовых полей и помощи пользователям в разработке собственных наборов параметров для химикатов, которые до сих пор не параметризованы.[34][35] Усилия по предоставлению открытых исходных кодов и методов включают: openMM и openMD. Использование полуавтоматики или полной автоматизации без участия химических знаний, вероятно, приведет к увеличению несоответствий на уровне атомных зарядов для определения оставшихся параметров и, вероятно, снизит интерпретируемость и эффективность параметров.
В Силовое поле интерфейса (IFF) предполагает одно-единственное выражение энергии для всех соединений за период (с вариантами 9-6 и 12-6 LJ) и использует строгую проверку со стандартизованными протоколами моделирования, которые обеспечивают полную интерпретируемость и совместимость параметров, а также высокую точность и доступ к неограниченным комбинациям соединений.[4]
Переносимость
Функциональные формы и наборы параметров определены разработчиками межатомных потенциалов и имеют переменные степени самосогласованность и переносимость. Когда функциональные формы потенциальных членов изменяются, параметры из одной межатомной потенциальной функции обычно не могут использоваться вместе с другой межатомной потенциальной функцией.[19] В некоторых случаях модификации могут быть сделаны с небольшими усилиями, например, между 9-6 потенциалами Леннарда-Джонса и 12-6 потенциалами Леннарда-Джонса.[9] Переходы от потенциалов Букингема к гармоническим потенциалам или от Встроенные модели атома для гармонических потенциалов, напротив, потребует многих дополнительных предположений и может оказаться невозможным.
Ограничения
Все межатомные потенциалы основаны на приближении и экспериментальных данных, поэтому их часто называют эмпирический. Производительность варьируется от более высокой точности, чем теория функционала плотности вычисления, с доступом к системам и шкалам времени в миллион раз больше, к случайным предположениям в зависимости от силового поля.[36] Использование точных представлений о химической связи в сочетании с воспроизводимыми экспериментальными данными и проверкой может привести к устойчивым межатомным потенциалам высокого качества с гораздо меньшим количеством параметров и допущений по сравнению с квантовыми методами уровня DFT.[37][38]
Возможные ограничения включают атомные заряды, также называемые точечными зарядами. Большинство силовых полей полагаются на точечные заряды для воспроизведения электростатического потенциала вокруг молекул, который хуже работает для анизотропных распределений заряда.[39] Лекарство состоит в том, что точечные обвинения имеют четкую интерпретацию,[12] и виртуальные электроны могут быть добавлены для захвата важных характеристик электронной структуры, таких как дополнительная поляризуемость в металлических системах для описания потенциала изображения, внутренних мультипольных моментов в π-сопряженных системах и неподеленных пар в воде.[40][41][42] Электронный поляризация среды можно лучше включить, используя поляризуемые силовые поля[43][44] или используя макроскопический диэлектрическая постоянная. Однако применение одного значения диэлектрической проницаемости является грубым приближением в сильно гетерогенных средах белков, биологических мембран, минералов или электролитов.[45]
Все виды силы Ван дер Ваальса также сильно зависят от окружающей среды, поскольку эти силы возникают в результате взаимодействия индуцированных и «мгновенных» диполей (см. Межмолекулярная сила). Оригинал Фриц Лондон теория этих сил применима только в вакууме. Более общая теория сил Ван-дер-Ваальса в конденсированных средах была разработана А. Д. Маклахланом в 1963 году и включает оригинальный подход Лондона как частный случай.[46] Теория Маклахлана предсказывает, что притяжение Ван-дер-Ваальса в СМИ слабее, чем в вакууме, и следует как растворяется как правило, которое означает, что разные типы атомов взаимодействуют слабее, чем атомы идентичных типов.[47] Это в отличие от комбинаторные правила или уравнение Слейтера-Кирквуда, применяемое для развития классических силовых полей. В комбинаторные правила утверждают, что энергия взаимодействия двух разнородных атомов (например, C… N) представляет собой среднее значение энергий взаимодействия соответствующих идентичных пар атомов (например, C… C и N… N). Согласно теории Маклахлана, взаимодействия частиц в среде могут быть даже полностью отталкивающими, как это наблюдается для жидкости. гелий,[46] однако отсутствие испарения и наличие точки замерзания противоречит теории чисто отталкивающих взаимодействий. Измерения сил притяжения между различными материалами (Постоянная Гамакера) были объяснены Яков Исраэлашвили.[46] Например, "взаимодействие между углеводородами через воду составляет около 10% от взаимодействия через вакуум".[46] Такие эффекты представлены в молекулярной динамике через парные взаимодействия, которые пространственно более плотны в конденсированной фазе по сравнению с газовой фазой и воспроизводятся после подтверждения параметров для всех фаз для воспроизведения химической связи, плотности и когезионной / поверхностной энергии.
Ощущались ограничения в уточнении структуры белка. Основная основная проблема - это огромное пространство конформации полимерных молекул, которое выходит за рамки современной вычислительной возможности, когда содержит более ~ 20 мономеров.[48] Участники Критическая оценка предсказания структуры белка (CASP) не пытался дорабатывать свои модели, чтобы избежать "основная проблема молекулярной механики, а именно то, что минимизация энергии или молекулярная динамика обычно приводит к модели, которая меньше похожа на экспериментальную структуру".[49] Силовые поля успешно применялись для уточнения структуры белков в различных Рентгеновская кристаллография и ЯМР-спектроскопия приложения, особенно с использованием программы XPLOR.[50] Однако уточнение обусловлено в основном набором экспериментальных ограничений, а межатомные потенциалы служат в основном для устранения межатомных препятствий. Результаты расчетов практически совпадают с потенциалами жестких сфер, реализованными в программе DYANA.[51] (расчеты по данным ЯМР) или с программами для кристаллографического уточнения, которые вообще не используют энергетические функции. Эти недостатки связаны с межатомными потенциалами и с невозможностью эффективно исследовать конформационное пространство больших молекул.[52] Таким образом, разработка параметров для решения таких крупномасштабных проблем требует новых подходов. Конкретная проблемная область моделирование гомологии белков.[53] Между тем, альтернативные эмпирические оценочные функции были разработаны для стыковка лигандов,[54] сворачивание белка,[55][56][57] уточнение модели гомологии,[58] вычислительный белковый дизайн,[59][60][61] и моделирование белков в мембранах.[62]
Также утверждалось, что некоторые силовые поля белка действуют с энергиями, не имеющими отношения к укладке белка или связыванию лиганда.[43] Параметры силовых полей белков воспроизводят энтальпия из сублимация, т.е. энергия испарения молекулярных кристаллов. Тем не мение, сворачивание белка и связывание лиганда термодинамически ближе к кристаллизация, или переходы жидкость-твердое тело, как эти процессы представляют замораживание подвижных молекул в конденсированных средах.[63][64][65] Таким образом, ожидается, что изменения свободной энергии во время сворачивания белка или связывания лиганда представляют собой комбинацию энергии, аналогичной теплота плавления (энергия, поглощенная при плавлении молекулярных кристаллов), a конформационная энтропия вклад, и сольватация свободная энергия. В теплота плавления значительно меньше энтальпии сублимации.[46] Следовательно, потенциалы, описывающие сворачивание белка или связывание лиганда, требуют более согласованных протоколов параметризации, например, как описано для IFF. Действительно, энергии Водородные связи в белках составляют ~ -1,5 ккал / моль при оценке из белковая инженерия или же альфа спираль к катушка данные перехода,[66][67] но те же энергии, оцененные из сублимация энтальпия молекулярных кристаллы были от -4 до -6 ккал / моль,[68] что связано с реформированием существующих водородных связей, а не с образованием водородных связей с нуля. Глубины модифицированного Потенциалы Леннарда-Джонса полученные из данных инженерии белков, также были меньше, чем в типичных потенциальных параметрах, и соответствовали как растворяется как правило, как это предсказывает теория Маклахлана.[43]
Широко используемые силовые поля
Разные силовые поля предназначены для разных целей. Все реализовано в различных компьютерах программного обеспечения.
MM2 был разработан Норман Аллинджер в основном для конформационного анализа углеводороды и другие небольшие органические молекулы. Он предназначен для максимально точного воспроизведения равновесной ковалентной геометрии молекул. Он реализует большой набор параметров, которые постоянно уточняются и обновляются для многих различных классов органических соединений (MM3 и MM4).[69][70][71][72][73]
CFF был разработан Арие Варшел, Лифсон и соавторы как общий метод для объединения исследований энергий, структур и колебаний общих молекул и молекулярных кристаллов. Программа CFF, разработанная Левиттом и Варшелом, основана на декартовом представлении всех атомов и послужила основой для многих последующих программ моделирования.
ECEPP был разработан специально для моделирования пептидов и белков. Он использует фиксированные геометрические формы аминокислотных остатков для упрощения поверхности потенциальной энергии. Таким образом, минимизация энергии проводится в пространстве торсионных углов белка. И MM2, и ECEPP включают потенциалы для водородных связей и потенциалы кручения для описания вращения вокруг одинарных связей. ECEPP / 3 был реализован (с некоторыми изменениями) в Механика внутренних координат и ФАНТОМ.[74]
ЯНТАРЬ, Очарование, и ГРОМОС были разработаны в основном для молекулярная динамика макромолекул, хотя они также обычно используются для минимизации энергии. Таким образом, координаты всех атомов рассматриваются как свободные переменные.
Силовое поле интерфейса (IFF)[75] был разработан как первое последовательное силовое поле для соединений в периодической таблице. Он преодолевает известные ограничения присвоения постоянных зарядов, использует стандартные условия в качестве эталонного состояния, воспроизводит структуры, энергии и производные энергии и количественно определяет ограничения для всех включенных соединений.[4][76] Он совместим с несколькими силовыми полями для моделирования гибридных материалов (CHARMM, AMBER, OPLS-AA, CFF, CVFF, GROMOS).
Классический
- ЯНТАРЬ (Assisted Model Building and Energy Refinement) - широко используется для белков и ДНК.
- CFF (Consistent Force Field) - семейство силовых полей, адаптированных к широкому спектру органических соединений, включая силовые поля для полимеров, металлов и т. Д.
- Очарование (Химия в HARvard Molecular Mechanics) - первоначально разработанная в Гарварде, широко используется как для малых молекул, так и для макромолекул.
- COSMOS-NMR - гибридное силовое поле QM / MM, адаптированное к множеству неорганических соединений, органических соединений и биологических макромолекул, включая полуэмпирический расчет атомных зарядов и свойств ЯМР. COSMOS-NMR оптимизирован для выяснения структуры на основе ЯМР и реализован в пакете молекулярного моделирования COSMOS.[77]
- CVFF - также широко используется для небольших молекул и макромолекул.[14]
- ECEPP[78] - первое силовое поле для полипептидных молекул - разработано Ф.А.Момани, Х.А. Шерага и его коллеги.[79][80]
- ГРОМОС (GROningen MOlecular Simulation) - силовое поле, которое входит в состав программного обеспечения GROMOS, универсального пакета компьютерного моделирования молекулярной динамики для исследования биомолекулярных систем.[81] Силовое поле GROMOS A-версия была разработана для применения к водным или аполярным растворам белков, нуклеотидов и сахаров. Также доступна версия B для моделирования изолированных молекул в газовой фазе.
- IFF (интерфейсное силовое поле) - первое силовое поле для покрытия металлов, минералов, 2D-материалов и полимеров на одной платформе с высочайшей точностью и совместимостью со многими другими силовыми полями (CHARMM, AMBER, OPLS-AA, CFF, CVFF, GROMOS) , включает 12-6 вариантов LJ и 9-6 LJ[4][75]
- MMFF (Молекулярное силовое поле Merck) - разработан в Merck для широкого круга молекул.
- OPLS (Оптимизированный потенциал для моделирования жидкостей) (варианты включают OPLS-AA, OPLS-UA, OPLS-2001, OPLS-2005) - разработано Уильям Л. Йоргенсен на химическом факультете Йельского университета.
- QCFF / PI - общие силовые поля для сопряженных молекул.[82][83]
- UFF (Универсальное силовое поле) - Общее силовое поле с параметрами для полной таблицы Менделеева, включая актиноиды, разработанное в Университете штата Колорадо.[21] Известно, что надежность низкая из-за отсутствия проверки и интерпретации параметров почти всех заявленных соединений, особенно металлов и неорганических соединений.[5][76]
Поляризуемый
- ЯНТАРЬ - поляризуемое силовое поле, разработанное Джимом Колдуэллом и сотрудниками.[84]
- AMOEBA (Atomic Multipole Optimized Energy for Biomolecular Applications) - силовое поле, разработанное Pengyu Ren (Техасский университет в Остине) и Jay W. Ponder (Вашингтонский университет).[85] Силовое поле AMOEBA постепенно переходит на более богатую физикой AMOEBA +.[86][87]
- CHARMM - поляризуемое силовое поле, разработанное С. Пателем (Университет штата Делавэр) и К. Л. Бруксом III (Университет штата Мичиган).[26][88] Основан на классическом осцилляторе Друде, разработанном А. МакКереллом (Мэрилендский университет, Балтимор) и Б. Ру (Чикагский университет).[89][90]
- CFF / ind и ENZYMIX - первое поляризуемое силовое поле[91] который впоследствии был использован во многих приложениях к биологическим системам.[44]
- COSMOS-ЯМР (компьютерное моделирование молекулярной структуры) - разработан Ульрихом Штернбергом и соавторами. Гибридное силовое поле QM / MM дает возможность явного квантово-механического расчета электростатических свойств с использованием локализованных орбиталей связи с помощью быстрого формализма BPT.[92] Флуктуация атомного заряда возможна на каждом этапе молекулярной динамики.
- DRF90 разработан P. Th. ван Дуйнен и его сотрудники.[93]
- IFF (Interface Force Field) - включает поляризуемость для металлов (Au, W) и pi-сопряженных молекул[25][42][41]
- NEMO (неэмпирическая молекулярная орбиталь) - процедура, разработанная Гуннаром Карлстремом и его коллегами из Лундского университета (Швеция)[94]
- PIPF - Поляризуемый межмолекулярный потенциал для жидкостей представляет собой индуцированное точечное дипольное силовое поле для органических жидкостей и биополимеров. Молекулярная поляризация основана на модели взаимодействующего диполя Тоула (TID) и была разработана Цзяли Гао. Исследовательская группа Гао | в Университете Миннесоты.[95][96]
- Поляризуемое силовое поле (PFF) - разработано Ричардом А. Фриснером с сотрудниками.[97]
- Уравнивание химического потенциала (CPE) на основе SP - подход, разработанный Р. Челли и П. Прокаччи.[98]
- PHAST - поляризуемый потенциал, разработанный Крисом Чиоче с сотрудниками.[99]
- ORIENT - процедура, разработанная Энтони Дж. Стоуном (Кембриджский университет) и соавторами.[100]
- Гауссовская электростатическая модель (GEM) - поляризуемое силовое поле, основанное на подгонке плотности, разработанное Томасом А. Дарденом и Г. Андресом Сиснеросом из NIEHS; и Жан-Филип Пикемаль из Университета Париж VI.[101][102][103]
- Атомистический поляризуемый потенциал для жидкостей, электролитов и полимеров (APPLE & P), разработанный Олегом Борогиным, Дмитрием Бедровым и его коллегами, который распространяется Wasatch Molecular Incorporated.[104]
- Поляризуемая процедура, основанная на подходе Ким-Гордона, разработанном Юргом Хуттером и соавторами (Университет Цюриха)[нужна цитата]
Реактивный
- EVB (Эмпирическая валентная связь) - это реактивное силовое поле, введенное Уоршелом и его сотрудниками, вероятно, является наиболее надежным и физически последовательным способом использования силовых полей при моделировании химических реакций в различных средах.[согласно кому?] EVB позволяет рассчитывать свободную энергию активации в конденсированных фазах и ферментах.
- ReaxFF - реактивное силовое поле (межатомный потенциал), разработанное Адри ван Дуином, Уильям Годдард и коллеги. Он медленнее, чем классический MD (50x), требует наборов параметров с конкретной валидацией и не имеет валидации для поверхностной и межфазной энергии. Параметры не интерпретируемы. Это может быть использовано для динамического моделирования химических реакций в атомистическом масштабе.[13] Распараллеленный ReaxFF позволяет проводить реактивное моделирование >> 1 000 000 атомов на больших суперкомпьютерах.
Крупнозернистый
- DPD (Диссипативная динамика частиц) - это метод, обычно применяемый в химической инженерии. Обычно он используется для изучения гидродинамики различных простых и сложных жидкостей, которые требуют рассмотрения масштабов времени и длины, больших, чем те, которые доступны классическим. Молекулярная динамика. Потенциал был первоначально предложен Хугербрюгге и Кельманом. [105][106] с более поздними модификациями Español и Warren [107] Текущее состояние дел хорошо задокументировано в CECAM мастерская в 2008 году.[108] Недавно была проведена работа по улавливанию некоторых химических субтитров, относящихся к растворам. Это привело к работе, в которой рассматривается автоматическая параметризация потенциалов взаимодействия DPD с экспериментальными наблюдаемыми.[35]
- МАРТИНИ - крупнозернистый потенциал, разработанный Марринк и его коллегами из Гронингенский университет, первоначально разработанная для молекулярно-динамического моделирования липидов,[3] позже распространился на различные другие молекулы. Силовое поле отображает четыре тяжелых атома на один сайт взаимодействия CG и параметризуется с целью воспроизведения термодинамических свойств.
- SIRAH - крупнозернистое силовое поле, разработанное Пантано и его коллегами из группы биомолекулярного моделирования Института Пастера в Монтевидео, Уругвай; разработан для молекулярной динамики воды, ДНК и белков. Бесплатно доступно для пакетов AMBER и GROMACS.
- VAMM (виртуальная атомная молекулярная механика) - крупнозернистое силовое поле, разработанное Коркутом и Хендриксоном для расчетов молекулярной механики, таких как крупномасштабные конформационные переходы, основанные на виртуальных взаимодействиях атомов C-альфа. Это силовое поле, основанное на знаниях, разработанное для захвата свойств, зависящих от вторичной структуры и специфичной для остатков контактной информации в белках.[109]
Машинное обучение
- ANI - это переносимый потенциал нейронной сети, построенный из векторов атомарного окружения и способный обеспечить точность DFT с точки зрения энергий.[110]
- FFLUX (первоначально QCTFF) [111] Набор обученных Кригинг модели, которые работают вместе, чтобы обеспечить молекулярное силовое поле, обученное на Атомы в молекулах или Энергетические термины квантовой химической топологии, включая электростатическую, обменную и электронную корреляцию.[112][113]
- TensorMol смешанная модель, Нейронная сеть обеспечивает краткосрочный потенциал, в то время как более традиционные потенциалы добавляют проверенные долгосрочные условия.[113]
- Δ-ML - это не метод силового поля, а модель, которая добавляет изученные поправочные параметры энергии к приближенным и относительно дешевым в вычислительном отношении квантово-химическим методам, чтобы обеспечить уровень точности более высокого порядка, более затратной в вычислительном отношении квантово-химической модели.[114]
- SchNet а Нейронная сеть использование сверточных слоев с непрерывным фильтром для прогнозирования химических свойств и поверхностей потенциальной энергии.[115]
- PhysNet - это энергетическая функция на основе нейронной сети, предназначенная для прогнозирования энергии, силы и (флуктуирующих) частичных зарядов.[116]
Вода
Набор параметров, используемых для моделирования воды или водных растворов (в основном силовое поле для воды), называется водная модель. Вода привлекает большое внимание из-за своих необычных свойств и важности как растворителя. Было предложено много водных моделей; некоторые примеры: TIP3P, TIP4P,[117] SPC, гибкая простая модель точечной воды (гибкий SPC), ST2 и мВт.[118] Другие растворители и методы представления растворителей также применяются в вычислительной химии и физике, некоторые примеры приведены на странице Модель растворителя. Недавно были опубликованы новые методы создания водных моделей.[119]
Модифицированные аминокислоты
- Forcefield_PTM - Силовое поле и веб-инструмент на основе AMBER для моделирования общих посттрансляционных модификаций аминокислот в белках, разработанные Крисом Флаудасом и его коллегами. Он использует модель заряда ff03 и имеет несколько поправок на кручение боковой цепи, параметризованных в соответствии с квантово-химической поверхностью вращения.[120]
- Forcefield_NCAA - Силовое поле на основе AMBER и веб-инструмент для моделирования общих неприродных аминокислот в белках в моделировании конденсированной фазы с использованием модели заряда ff03.[121] Сообщается, что заряды коррелируют с энергиями без гидратации соответствующих аналогов боковой цепи.[122]
Другой
- LFMM (молекулярная механика поля лигандов)[123] - функции для координационной сферы вокруг переходных металлов на основе модели углового перекрытия (AOM). Реализован в молекулярной операционной среде (MOE) как DommiMOE и в Тинкер[124]
- VALBOND - функция гибки под углом, основанная на теория валентной связи и работает при больших угловых искажениях, гипервалентные молекулы, и комплексы переходных металлов. Он может быть включен в другие силовые поля, такие как CHARMM и UFF.
Смотрите также
- Сравнение реализаций силового поля
- Молекулярная динамика
- Молекулярная механика
- Программное обеспечение для молекулярного дизайна
- Молекулярное моделирование
- Сравнение программного обеспечения для моделирования молекулярной механики
- Статистический потенциал
- Межатомный потенциал
- Потенциал ордеров на облигации
- Встроенная модель атома
Рекомендации
- ^ Френкель Д (2007). Понимание молекулярного моделирования: от алгоритмов к приложениям. Академическая пресса. ISBN 978-0-12-267351-1. OCLC 254835355.
- ^ а б Выщелачивание А (30 января 2001 г.). Молекулярное моделирование: принципы и приложения (2-е изд.). Харлоу: Прентис Холл. ISBN 9780582382107.
- ^ а б Марринк С.Дж., Рисселада Х.Дж., Ефимов С., Тилеман Д.П., де Фрис А.Х. (июль 2007 г.). «Силовое поле MARTINI: крупнозернистая модель для биомолекулярного моделирования» (PDF). Журнал физической химии B. 111 (27): 7812–24. Дои:10.1021 / jp071097f. PMID 17569554.
- ^ а б c d е ж грамм час я j Хайнц Х., Лин Т.Дж., Мишра РК, Эмами Ф.С. (февраль 2013 г.). «Термодинамически согласованные силовые поля для сборки неорганических, органических и биологических наноструктур: силовое поле ИНТЕРФЕЙСА». Langmuir. 29 (6): 1754–65. Дои:10.1021 / la3038846. PMID 23276161.
- ^ а б Хайнц Х., Кернер Х., Андерсон К.Л., Вайя Р.А., Фермер Б.Л. (ноябрь 2005 г.). «Силовое поле для силикатов типа слюды и динамика цепей октадециламмония, привитых к монтмориллониту». Химия материалов. 17 (23): 5658–5669. Дои:10,1021 / см 0509328. ISSN 0897-4756.
- ^ а б Сан Х., Мамби С.Дж., Мейпл Дж.Р., Хаглер А.Т. (апрель 1994 г.). "Ab Initio CFF93 All-Atom Force Field для поликарбонатов". Журнал Американского химического общества. 116 (7): 2978–2987. Дои:10.1021 / ja00086a030. ISSN 0002-7863.
- ^ Хуанг Дж., Маккерелл А.Д. (сентябрь 2013 г.). "Полностью атомное аддитивное силовое поле белка CHARMM36: проверка на основе сравнения с данными ЯМР". Журнал вычислительной химии. 34 (25): 2135–45. Дои:10.1002 / jcc.23354. ЧВК 3800559. PMID 23832629.
- ^ Ван Дж., Вольф Р.М., Колдуэлл Дж. В., Коллман П.А., Дело DA (июль 2004 г.). «Разработка и тестирование общего янтарного силового поля». Журнал вычислительной химии. 25 (9): 1157–74. Дои:10.1002 / jcc.20035. PMID 15116359.
- ^ а б Мишра РК, Фернандес-Карраско Л., Флатт Р. Дж., Хайнц Х (июль 2014 г.). «Силовое поле для трикальцийалюмината для характеристики свойств поверхности, начальной гидратации и органически модифицированных границ раздела в атомном разрешении». Dalton Transactions. 43 (27): 10602–16. Дои:10.1039 / c4dt00438h. HDL:2117/24209. PMID 24828263.
- ^ Гросс К.К., Сейболд П.Г., Хадад К.М. (2002). «Сравнение различных схем атомного заряда для прогнозирования вариаций pKa в замещенных анилинах и фенолах». Международный журнал квантовой химии. 90 (1): 445–458. Дои:10.1002 / qua.10108. ISSN 0020-7608.
- ^ Ван Б., Ли С.Л., Трулар Д.Г. (декабрь 2014 г.). «Моделирование частичных атомных зарядов в неорганических металлических молекулах и твердых телах и перераспределения заряда в литий-ионных катодах». Журнал химической теории и вычислений. 10 (12): 5640–50. Дои:10.1021 / ct500790p. PMID 26583247.
- ^ а б c d Heinz H, Suter UW (ноябрь 2004 г.). «Атомные заряды для классического моделирования полярных систем». Журнал физической химии B. 108 (47): 18341–18352. Bibcode:2004APS..MAR.Y8006H. Дои:10.1021 / jp048142t. ISSN 1520-6106.
- ^ а б van Duin AC, Dasgupta S, Lorant F, Годдард WA (2001). «ReaxFF: реактивное силовое поле для углеводородов» (PDF). Журнал физической химии A. 105 (41): 9396–9409. Bibcode:2001JPCA..105.9396V. CiteSeerX 10.1.1.507.6992. Дои:10.1021 / jp004368u.
- ^ а б c Dauber-Osguthorpe P, Робертс VA, Osguthorpe DJ, Wolff J, Genest M, Hagler AT (1988). «Структура и энергетика связывания лиганда с белками: дигидрофолатредуктаза-триметоприм Escherichia coli, система лекарство-рецептор». Белки. 4 (1): 31–47. Дои:10.1002 / prot.340040106. PMID 3054871.
- ^ Дхармавардхана ЧЧ, Канхайя К., Линь Т., Гарли А., Кнехт М.Р., Чжоу Дж., Мяо Дж., Хайнц Х (19.06.2017). «Надежный вычислительный дизайн биологических-неорганических материалов в крупном нанометровом масштабе с использованием Interface-FF». Молекулярное моделирование. 43 (13–16): 1394–1405. Дои:10.1080/08927022.2017.1332414. ISSN 0892-7022.
- ^ Лю Дж., Теннессен Э., Мяо Дж., Хуанг Й., Рондинелли Дж. М., Хайнц Х. (31.05.2018). «Понимание химической связи в сплавах и представление в атомных моделированиях». Журнал физической химии C. 122 (26): 14996–15009. Дои:10.1021 / acs.jpcc.8b01891. ISSN 1932-7447.
- ^ Хайнц Х., Вайя Р.А., Фермер Б.Л., Наик Р.Р. (2008-10-09). «Точное моделирование поверхностей и границ раздела гранецентрированных кубических металлов с использованием 12-6 и 9-6 потенциалов Леннарда-Джонса». Журнал физической химии C. 112 (44): 17281–17290. Дои:10.1021 / jp801931d. ISSN 1932-7447.
- ^ Эмами Ф.С., Пудду В., Берри Р.Дж., Варшней В., Патвардхан С.В., Перри С.К., Хайнц Х. (02.04.2014). «Силовое поле и база данных моделей поверхности кремнезема для моделирования межфазных свойств в атомном разрешении» (PDF). Химия материалов. 26 (8): 2647–2658. Дои:10,1021 / см 500365c. ISSN 0897-4756.
- ^ а б Хайнц Х., Рамезани-Дахель Х. (январь 2016 г.). «Моделирование неорганических-биоорганических интерфейсов для открытия новых материалов: идеи, сравнения с экспериментом, проблемы и возможности». Обзоры химического общества. 45 (2): 412–48. Дои:10.1039 / c5cs00890e. PMID 26750724.
- ^ Йоргенсен В.Л., Максвелл Д.С., Тирадо-Ривес Дж. (Январь 1996 г.). «Разработка и испытание полностью атомного силового поля OPLS по конформационной энергии и свойствам органических жидкостей». Журнал Американского химического общества. 118 (45): 11225–11236. Дои:10.1021 / ja9621760. ISSN 0002-7863.
- ^ а б Раппе А.К., Касевит С.Дж., Колвелл К.С., Годдард III ВА, Скифф В.М. (декабрь 1992 г.). "UFF, полное силовое поле периодической таблицы для молекулярной механики и моделирования молекулярной динамики". Журнал Американского химического общества. 114 (25): 10024–10035. Дои:10.1021 / ja00051a040. ISSN 0002-7863.
- ^ Дик Б.Г., Оверхаузер А.В. (1958-10-01). «Теория диэлектрической проницаемости щелочно-галогенидных кристаллов». Физический обзор. 112 (1): 90–103. Bibcode:1958ПхРв..112 ... 90Д. Дои:10.1103 / Physrev.112.90. ISSN 0031-899X.
- ^ Митчелл П.Дж., Финчем Д. (22 февраля 1993 г.). «Моделирование оболочки с помощью адиабатической динамики». Журнал физики: конденсированное вещество. 5 (8): 1031–1038. Bibcode:1993JPCM .... 5.1031M. Дои:10.1088/0953-8984/5/8/006. ISSN 0953-8984.
- ^ Ю Х, ван Гунстерен В. Ф. (ноябрь 2005 г.). «Учет поляризации в молекулярном моделировании». Компьютерная физика Коммуникации. 172 (2): 69–85. Bibcode:2005CoPhC.172 ... 69Y. Дои:10.1016 / j.cpc.2005.01.022. ISSN 0010-4655.
- ^ а б c Геада, Иллинойс, Рамезани-Дахель Х, Джамиль Т., Сульпизи М, Хайнц Х (февраль 2018 г.). «Понимание индуцированных зарядов на металлических поверхностях и биоинтерфейсах с использованием поляризуемого потенциала Леннарда-Джонса». Nature Communications. 9 (1): 716. Bibcode:2018НатКо ... 9..716G. Дои:10.1038 / s41467-018-03137-8. ЧВК 5818522. PMID 29459638.
- ^ а б Патель С., Брукс С.Л. (январь 2004 г.). "Поле силы флуктуирующего заряда CHARMM для белков: параметризация и применение для моделирования объемных органических жидкостей". Журнал вычислительной химии. 25 (1): 1–15. Дои:10.1002 / jcc.10355. PMID 14634989.
- ^ Лин Т, Хайнц Х (26 февраля 2016). «Точные параметры силового поля и модели поверхности с разрешением pH для гидроксиапатита для понимания структуры, механики, гидратации и биологических интерфейсов». Журнал физической химии C. 120 (9): 4975–4992. arXiv:1512.00122. Дои:10.1021 / acs.jpcc.5b12504. ISSN 1932-7447. S2CID 51913034.
- ^ Лемкул Дж. А., Хуанг Дж., Ру Б., МакКерелл А. Д. (май 2016 г.). «Эмпирическое поляризуемое силовое поле на основе классической модели осциллятора Друде: история развития и недавние приложения». Химические обзоры. 116 (9): 4983–5013. Дои:10.1021 / acs.chemrev.5b00505. ЧВК 4865892. PMID 26815602.
- ^ Лоренц HA (1905). «Движение электронов в металлических телах, I.». Proc. К. Нед. Акад. Смачивать. 7: 451. Bibcode:1904КНАБ .... 7..438Л.
- ^ а б Друде П. (1900). "Zur Elekronentheorie der Metalle. I. Teil". Энн Физ. 306 (3): 566–613. Дои:10.1002 / andp.19003060312.
- ^ Сиу С.В., Плугацкова К., Бёкманн Р.А. (апрель 2012 г.). «Оптимизация силового поля OPLS-AA для длинных углеводородов». Журнал химической теории и вычислений. 8 (4): 1459–70. Дои:10.1021 / ct200908r. PMID 26596756.
- ^ Адури Р., Псюк Б.Т., Саро П., Танига Х., Шлегель Н.Б., Санта-Люсия Дж. (Июль 2007 г.). «Параметры силового поля AMBER для естественно встречающихся модифицированных нуклеозидов в РНК». Журнал химической теории и вычислений. 3 (4): 1464–75. Дои:10.1021 / ct600329w. PMID 26633217.
- ^ Киршнер К.Н., Линс Р.Д., Маасс А., Соарес Т.А. (ноябрь 2012 г.). «Силовое поле на основе гликама для моделирования липополисахаридных мембран: параметризация и проверка». Журнал химической теории и вычислений. 8 (11): 4719–31. Дои:10.1021 / ct300534j. PMID 26605626.
- ^ Ван LP, Мартинес Т.Дж., Панде В.С. (июнь 2014 г.). «Создание силовых полей: автоматический, систематический и воспроизводимый подход». Письма в Журнал физической химии. 5 (11): 1885–91. Дои:10.1021 / jz500737m. PMID 26273869.
- ^ а б МакДонах Дж. Л., Шкурти А., Брей DJ, Андерсон Р. Л., Пайзер-Кнапп Е. О. (октябрь 2019 г.). «Использование машинного обучения для эффективной параметризации крупнозернистых молекулярных силовых полей». Журнал химической информации и моделирования. 59 (10): 4278–4288. Дои:10.1021 / acs.jcim.9b00646. PMID 31549507.
- ^ Эмами Ф.С., Пудду В., Берри Р.Дж., Варшней В., Патвардхан С.В., Перри С.К., Хайнц Х. (22.04.2014). «Силовое поле и база данных моделей поверхности кремнезема для моделирования межфазных свойств в атомном разрешении» (PDF). Химия материалов. 26 (8): 2647–2658. Дои:10,1021 / см 500365c. ISSN 0897-4756.
- ^ Руис В.Г., Лю В., Ткаченко А. (2016-01-15). "Теория функционала плотности с экранированными ван-дер-ваальсовыми взаимодействиями применительно к атомным и молекулярным адсорбатам на плотноупакованных и неплотноупакованных поверхностях". Физический обзор B. 93 (3): 035118. Bibcode:2016PhRvB..93c5118R. Дои:10.1103 / Physrevb.93.035118. HDL:11858 / 00-001M-0000-0029-3035-8. ISSN 2469-9950.
- ^ Руис В.Г., Лю В., Зойер Э., Шеффлер М., Ткаченко А. (апрель 2012 г.). «Плотно-функциональная теория с экранированными ван-дер-ваальсовыми взаимодействиями для моделирования гибридных неорганико-органических систем». Письма с физическими проверками. 108 (14): 146103. Bibcode:2012ПхРвЛ.108н6103Р. Дои:10.1103 / Physrevlett.108.146103. PMID 22540809.
- ^ Крамер К., Спинн А., Лидл К.Р. (октябрь 2014 г.). «Анизотропия заряда: где атомные мультиполи имеют наибольшее значение». Журнал химической теории и вычислений. 10 (10): 4488–96. Дои:10.1021 / ct5005565. PMID 26588145.
- ^ Махони М.В., Йоргенсен В.Л. (22 мая 2000 г.). «Пятиузельная модель жидкой воды и воспроизведение аномалии плотности с помощью жестких, неполяризуемых потенциальных функций». Журнал химической физики. 112 (20): 8910–8922. Bibcode:2000ЖЧФ.112.8910М. Дои:10.1063/1.481505. ISSN 0021-9606.
- ^ а б Xu R, Chen CC, Wu L, Scott MC, Theis W., Ophus C и др. (Ноябрь 2015 г.). «Трехмерные координаты отдельных атомов в материалах, выявленные с помощью электроники». Материалы Природы. 14 (11): 1099–103. arXiv:1505.05938. Bibcode:2015НатМа..14.1099X. Дои:10.1038 / nmat4426. PMID 26390325. S2CID 5455024.
- ^ а б Праманик С., Гиссинджер-младший, Кумар С., Хайнц Х. (декабрь 2017 г.). «Дисперсия углеродных нанотрубок в растворителях и растворах полимеров: механизмы, сборка и предпочтения». САУ Нано. 11 (12): 12805–12816. Дои:10.1021 / acsnano.7b07684. PMID 29179536.
- ^ а б c Ломизе А.Л., Рейбарх М.Ю., Погожева И.Д. (август 2002 г.). «Межатомные потенциалы и параметры сольватации из данных белковой инженерии для захороненных остатков». Белковая наука. 11 (8): 1984–2000. Дои:10.1110 / л.с. 0307002. ЧВК 2373680. PMID 12142453.
- ^ а б Варшел А., Шарма П. К., Като М., Парсон В. В. (ноябрь 2006 г.). «Моделирование электростатических эффектов в белках». Biochimica et Biophysica Acta (BBA) - Белки и протеомика. 1764 (11): 1647–76. Дои:10.1016 / j.bbapap.2006.08.007. PMID 17049320.
- ^ Schutz CN, Warshel A (сентябрь 2001 г.). «Каковы диэлектрические« константы »белков и как проверить электростатические модели?». Белки. 44 (4): 400–17. Дои:10.1002 / prot.1106. PMID 11484218.
- ^ а б c d е Исраэлачвили Ю.Н. (2011). Межмолекулярные и поверхностные силы. Эльзевир. стр. iii. Дои:10.1016 / b978-0-12-391927-4.10024-6. ISBN 978-0-12-391927-4.
- ^ Leckband D, Israelachvili J (май 2001 г.). «Межмолекулярные силы в биологии». Ежеквартальные обзоры биофизики. 34 (2): 105–267. Дои:10.1017 / S0033583501003687. PMID 11771120.
- ^ Праманик С., Джамиль Т., Гиссинджер Дж. Р., Гиттет Д., Ариас-Монье П. Дж., Кумар С., Хайнц Х (2019-10-03). «Взаимодействие полиакрилонитрила с углеродными нанотрубками в растворе: конформации и связывание в зависимости от растворителя, температуры и концентрации». Современные функциональные материалы. 29 (50): 1905247. Дои:10.1002 / adfm.201905247. ISSN 1616-301X.
- ^ Кёль П., Левитт М. (февраль 1999 г.). «Лучшее будущее для предсказания структуры белка». Структурная биология природы. 6 (2): 108–11. Дои:10.1038/5794. PMID 10048917. S2CID 3162636.
- ^ Брюнгер А.Т., Адамс П.Д. (июнь 2002 г.). «Молекулярная динамика применительно к уточнению структуры рентгеновских лучей». Отчеты о химических исследованиях. 35 (6): 404–12. Дои:10.1021 / ar010034r. PMID 12069625.
- ^ Гюнтерт П. (май 1998 г.). «Расчет структуры биологических макромолекул по данным ЯМР». Ежеквартальные обзоры биофизики. 31 (2): 145–237. Дои:10.1017 / S0033583598003436. PMID 9794034. S2CID 43575627.
- ^ Остермейр К., Захариас М. (январь 2013 г.). «163 Улучшенный отбор образцов пептидов и белков с новым методом обмена репликами смещения». Журнал биомолекулярной структуры и динамики. 31 (sup1): 106. Дои:10.1080/07391102.2013.786405. ISSN 0739-1102. S2CID 98441607.
- ^ Трамонтано А, Мореа V (2003). «Оценка предсказаний на основе гомологии в CASP5». Белки. 53 Дополнение 6: 352–68. Дои:10.1002 / prot.10543. PMID 14579324.
- ^ Гольке Х., Клебе Г. (август 2002 г.). «Подходы к описанию и предсказанию сродства связывания низкомолекулярных лигандов с макромолекулярными рецепторами». Angewandte Chemie. 41 (15): 2644–76. Дои:10.1002 / 1521-3773 (20020802) 41:15 <2644 :: AID-ANIE2644> 3.0.CO; 2-O. PMID 12203463.
- ^ Эджкомб С.П., Мерфи КП (февраль 2000 г.). «Структурная энергетика сворачивания и связывания белков». Текущее мнение в области биотехнологии. 11 (1): 62–6. Дои:10.1016 / s0958-1669 (99) 00055-5. PMID 10679345.
- ^ Лазаридис Т., Карплюс М. (апрель 2000 г.). «Эффективные энергетические функции для предсказания структуры белков». Текущее мнение в структурной биологии. 10 (2): 139–45. Дои:10.1016 / s0959-440x (00) 00063-4. PMID 10753811.
- ^ Джавидпур Л. (2012). «Компьютерное моделирование сворачивания белков». Вычислительная техника в науке и технике. 14 (2): 97–103. Bibcode:2012CSE .... 14b..97J. Дои:10.1109 / MCSE.2012.21. S2CID 17613729.
- ^ Кригер Э, Джу К., Ли Дж, Ли Дж, Раман С., Томпсон Дж и др. (2009). «Повышение физического реализма, стереохимии и точности боковой цепи при моделировании гомологии: четыре подхода, хорошо зарекомендовавшие себя в CASP8». Белки. 77 Дополнение 9: 114–22. Дои:10.1002 / prot.22570. ЧВК 2922016. PMID 19768677.
- ^ Гордон Д.Б., Маршалл С.А., Майо С.Л. (август 1999 г.). «Энергетические функции для дизайна белков». Текущее мнение в структурной биологии. 9 (4): 509–13. Дои:10.1016 / S0959-440X (99) 80072-4. PMID 10449371.
- ^ Мендес Дж., Геруа Р., Серрано Л. (август 2002 г.). «Энергетическая оценка в белковом дизайне». Текущее мнение в структурной биологии. 12 (4): 441–6. Дои:10.1016 / s0959-440x (02) 00345-7. PMID 12163065.
- ^ Rohl CA, Strauss CE, Misura KM, Baker D (2004). «Прогнозирование структуры белка с помощью Rosetta». Численные компьютерные методы, часть D. Методы в энзимологии. 383. С. 66–93. Дои:10.1016 / S0076-6879 (04) 83004-0. ISBN 9780121827885. PMID 15063647.
- ^ Ломизе А.Л., Погожева И.Д., Ломизе М.А., Мосберг Н.И. (июнь 2006 г.). «Размещение белков в мембранах: вычислительный подход». Белковая наука. 15 (6): 1318–33. Дои:10.1110 / пс 062126106. ЧВК 2242528. PMID 16731967.
- ^ Мерфи КП, Гилл С.Дж. (декабрь 1991 г.). «Твердые модельные соединения и термодинамика разворачивания белков». Журнал молекулярной биологии. 222 (3): 699–709. Дои:10.1016/0022-2836(91)90506-2. PMID 1660931.
- ^ Шахнович Е.И., Финкельштейн А.В. (октябрь 1989 г.). «Теория кооперативных переходов в белковых молекулах. I. Почему денатурация глобулярного белка - это фазовый переход первого рода». Биополимеры. 28 (10): 1667–80. Дои:10.1002 / bip.360281003. PMID 2597723.
- ^ Грациано Г., Катанцано Ф, Дель Веккьо П., Джанкола С., Бароне Дж. (1996). «Термодинамическая стабильность глобулярных белков: надежная модель из исследований малых молекул». Gazetta Chim. Italiana. 126: 559–567.
- ^ Майерс Дж. К., Пейс С. Н. (октябрь 1996 г.). «Водородная связь стабилизирует глобулярные белки». Биофизический журнал. 71 (4): 2033–9. Bibcode:1996BpJ .... 71.2033M. Дои:10.1016 / S0006-3495 (96) 79401-8. ЧВК 1233669. PMID 8889177.
- ^ Scholtz JM, Marqusee S, Baldwin RL, York EJ, Stewart JM, Santoro M, Bolen DW (апрель 1991). «Калориметрическое определение изменения энтальпии для альфа-спирали, чтобы клубок перехода аланинового пептида в воде». Труды Национальной академии наук Соединенных Штатов Америки. 88 (7): 2854–8. Bibcode:1991ПНАС ... 88.2854С. Дои:10.1073 / пнас.88.7.2854. ЧВК 51338. PMID 2011594.
- ^ Гавеццотти А., Филиппини Г. (май 1994 г.). «Геометрия межмолекулярной водородной связи XH. Cntdot .. cntdot .. cntdot. Y (X, Y = N, O) и калибровка эмпирических потенциалов водородной связи». Журнал физической химии. 98 (18): 4831–7. Дои:10.1021 / j100069a010.
- ^ Аллингер Н.Л. (декабрь 1977 г.). «Конформационный анализ. 130. MM2. Углеводородное силовое поле, использующее скручивающие условия V1 и V2». Журнал Американского химического общества. 99 (25): 8127–34. Дои:10.1021 / ja00467a001.
- ^ «Домашняя страница MM2 и MM3». Архивировано из оригинал 23 января 2009 г.
- ^ Аллинджер Н.Л., Юх Ю.Х., Лии Дж.Х. (ноябрь 1989 г.). «Молекулярная механика. Силовое поле ММ3 для углеводородов. 1». Журнал Американского химического общества. 111 (23): 8551–66. Дои:10.1021 / ja00205a001.
- ^ Лии Дж. Х., Аллингер Н. Л. (ноябрь 1989 г.). «Молекулярная механика. Силовое поле ММ3 для углеводородов. 2. Частоты колебаний и термодинамика». Журнал Американского химического общества. 111 (23): 8566–75. Дои:10.1021 / ja00205a002.
- ^ Лии Дж. Х., Аллингер Н. Л. (ноябрь 1989 г.). «Молекулярная механика. Силовое поле MM3 для углеводородов. 3. Потенциалы Ван-дер-Ваальса и данные кристаллов для алифатических и ароматических углеводородов». Журнал Американского химического общества. 111 (23): 8576–82. Дои:10.1021 / ja00205a003.
- ^ Шауманн Т., Браун В., Вютрих К. (март 1990 г.). «Программа FANTOM для энергетической очистки полипептидов и белков с использованием минимизатора Ньютона – Рафсона в пространстве торсионных углов». Биополимеры. 29 (4–5): 679–94. Дои:10.1002 / bip.360290403.
- ^ а б "Силовое поле интерфейса (IFF)". Лаборатория Хайнца.
- ^ а б Мишра Р.К., Мохамед А.К., Гейссбюлер Д., Манзано Х., Джамиль Т., Шахсавари Р., Калиничев А.Г., Галмарини С., Тао Л., Хайнц Х., Пелленк Р. (декабрь 2017 г.). «База данных силового поля для цементных материалов, включая валидации, приложения и возможности» (PDF). Цемент и бетонные исследования. 102: 68–89. Дои:10.1016 / j.cemconres.2017.09.003.
- ^ Möllhoff M, Sternberg U (май 2001 г.). «Молекулярная механика с флуктуирующими атомными зарядами - новое силовое поле с полуэмпирическим расчетом заряда». Ежегодное молекулярное моделирование. 7 (4): 90–102. Дои:10.1007 / s008940100008. S2CID 91705326.
- ^ «ЭКЭПП». biohpc.cornell.edu.
- ^ Momany FA, McGuire RF, Burgess AW, Scheraga HA (октябрь 1975 г.). «Энергетические параметры в полипептидах. VII. Геометрические параметры, частичные атомные заряды, несвязанные взаимодействия, взаимодействия водородных связей и внутренние торсионные потенциалы для встречающихся в природе аминокислот». Журнал физической химии. 79 (22): 2361–81. Дои:10.1021 / j100589a006.
- ^ Арнаутова Ю.А., Ягельская А., Щерага Н.А. (март 2006 г.). «Новое силовое поле (ECEPP-05) для пептидов, белков и органических молекул». Журнал физической химии B. 110 (10): 5025–44. Дои:10.1021 / jp054994x. PMID 16526746.
- ^ "ГРОМОС". www.igc.ethz.ch.
- ^ Варшел А (1973). «Метод квантово-механического согласованного силового поля (QCFF / PI): расчеты энергий, конформаций и вибронных взаимодействий основного и возбужденного состояний сопряженных молекул». Израильский химический журнал. 11 (5): 709–17. Дои:10.1002 / ijch.197300067.
- ^ Варшел А, Левитт М (1974). QCFF / PI: Программа согласованной оценки силового поля равновесных геометрий и частот колебаний молекул (отчет). Университет Индианы: обмен программами по квантовой химии. п. КСРП 247.
- ^ Yang L, Tan CH, Hsieh MJ, Wang J, Duan Y, Cieplak P, Caldwell J, Kollman PA, Luo R (июль 2006 г.). «Янтарное силовое поле объединенного атома нового поколения». Журнал физической химии B. 110 (26): 13166–76. Дои:10.1021 / jp060163v. PMID 16805629.
- ^ "Пакет молекулярного моделирования Тинкер". dasher.wustl.edu.
- ^ Лю С., Пикемал Дж. П., Рен П. (январь 2020 г.). «Реализация зависящего от геометрии потока заряда в поляризуемом потенциале AMOEBA +». Письма в Журнал физической химии. 11 (2): 419–426. Дои:10.1021 / acs.jpclett.9b03489. PMID 31865706.
- ^ Лю С., Piquemal JP, Рен П. (июль 2019 г.). «Классический потенциал AMOEBA + для моделирования молекулярных взаимодействий». Журнал химической теории и вычислений. 15 (7): 4122–4139. Дои:10.1021 / acs.jctc.9b00261. ЧВК 6615954. PMID 31136175.
- ^ Патель С., Маккерелл А. Д., Брукс С. Л. (сентябрь 2004 г.). «Силовое поле флуктуирующего заряда CHARMM для белков: II свойства белка / растворителя из молекулярно-динамического моделирования с использованием неаддитивной электростатической модели». Журнал вычислительной химии. 25 (12): 1504–14. Дои:10.1002 / jcc.20077. PMID 15224394.
- ^ Анисимов В.М., Ламурё Г., Воробьев И.В., Хуанг Н., Ру Б., МакКерелл А.Д. (январь 2005 г.). «Определение электростатических параметров поляризуемого силового поля на основе классического осциллятора Друде». Журнал химической теории и вычислений. 1 (1): 153–68. Дои:10.1021 / ct049930p. PMID 26641126.
- ^ Ю. Х., Уитфилд Т.В., Хардер Э., Ламурё Г., Воробьев И., Анисимов В.М., Маккерелл А.Д., Ру Б. (2010). "Моделирование одновалентных и двухвалентных ионов в водном растворе с использованием поляризуемого силового поля Друде". Журнал химической теории и вычислений. 6 (3): 774–786. Дои:10.1021 / ct900576a. ЧВК 2838399. PMID 20300554.
- ^ Варшел А., Левитт М. (май 1976 г.). «Теоретические исследования ферментативных реакций: диэлектрическая, электростатическая и стерическая стабилизация иона карбония в реакции лизоцима». Журнал молекулярной биологии. 103 (2): 227–49. Дои:10.1016/0022-2836(76)90311-9. PMID 985660.
- ^ Штернберг У., Кох Ф. Т., Мёлльхофф М. (май 1994 г.). «Новый подход к полуэмпирическому расчету атомных зарядов для полипептидов и больших молекулярных систем». Журнал вычислительной химии. 15 (5): 524–31. Дои:10.1002 / jcc.540150505.
- ^ Сварт М., ван Дуйнен П. Т. (май 2006 г.). «DRF90: поляризуемое силовое поле». Молекулярное моделирование. 32 (6): 471–84. Дои:10.1080/08927020600631270.
- ^ Engkvist O, Astrand PO, Karlström G (ноябрь 2000 г.). «Точные межмолекулярные потенциалы, полученные из молекулярных волновых функций: устранение разрыва между квантовой химией и молекулярным моделированием». Химические обзоры. 100 (11): 4087–108. Дои:10.1021 / cr9900477. PMID 11749341.
- ^ Гао Дж., Хабиболлазаде Д., Шао Л. (ноябрь 1995 г.). «Поляризуемая межмолекулярная потенциальная функция для моделирования жидких спиртов». Журнал физической химии. 99 (44): 16460–7. Дои:10.1021 / j100044a039.
- ^ Се В., Пу Дж., Маккерелл А.Д., Гао Дж. (2007). «Разработка поляризуемой межмолекулярной потенциальной функции (PIPF) для жидких амидов и алканов». Журнал химической теории и вычислений. 3 (6): 1878–1889. Дои:10.1021 / ct700146x. ЧВК 2572772. PMID 18958290.
- ^ Maple JR, Cao Y, Damm W., Halgren TA, Kaminski GA, Zhang LY, Friesner RA (июль 2005 г.). "Поляризуемое силовое поле и методология сольватации континуума для моделирования белок-лигандных взаимодействий". Журнал химической теории и вычислений. 1 (4): 694–715. Дои:10.1021 / ct049855i. PMID 26641692.
- ^ Челли Р., Прокаччи П. (ноябрь 2002 г.). «Переносимое поляризуемое электростатическое силовое поле для молекулярной механики, основанное на принципе выравнивания химического потенциала». Журнал химической физики. 117 (20): 9175–89. Bibcode:2002ЖЧФ.117.9175С. Дои:10.1063/1.1515773.
- ^ Cioce CR, McLaughlin K, Belof JL, Space B (декабрь 2013 г.). «Поляризуемый и переносимый потенциал PHAST N2 для использования в моделировании материалов». Журнал химической теории и вычислений. 9 (12): 5550–7. Дои:10.1021 / ct400526a. PMID 26592288.
- ^ "Энтони Стоун: Компьютерные программы". www-stone.ch.cam.ac.uk.
- ^ Греш Н., Сиснерос Г.А., Дарден Т.А., Пикемал Дж.П. (ноябрь 2007 г.). "Анизотропные поляризуемые молекулярно-механические исследования меж- и внутримолекулярных взаимодействий и комплексов лиганд-макромолекула. Стратегия снизу вверх". Журнал химической теории и вычислений. 3 (6): 1960–1986. Дои:10.1021 / ct700134r. ЧВК 2367138. PMID 18978934.
- ^ Piquemal JP, Cisneros GA, Reinhardt P, Gresh N, Darden TA (март 2006 г.). «К силовому полю, основанному на подгонке плотности». Журнал химической физики. 124 (10): 104101. Bibcode:2006ЖЧФ.124дж4101П. Дои:10.1063/1.2173256. ЧВК 2080832. PMID 16542062.
- ^ Cisneros GA, Piquemal JP, Darden TA (ноябрь 2006 г.). «Обобщение гауссовой электростатической модели: расширение на произвольный угловой момент, распределенные мультиполи и ускорение с помощью методов обратного пространства». Журнал химической физики. 125 (18): 184101. Bibcode:2006ЖЧФ.125р4101С. Дои:10.1063/1.2363374. ЧВК 2080839. PMID 17115732.
- ^ Бородин О. (август 2009 г.). «Моделирование развития поляризуемых силовых полей и молекулярной динамики ионных жидкостей». Журнал физической химии B. 113 (33): 11463–78. Дои:10.1021 / jp905220k. PMID 19637900.
- ^ Hoogerbrugge PJ, Koelman JM (1992). "Моделирование микроскопических гидродинамических явлений с помощью диссипативной динамики частиц". Письма Europhysics (EPL). 19 (3): 155–160. Bibcode:1992EL ..... 19..155H. Дои:10.1209/0295-5075/19/3/001. ISSN 0295-5075.
- ^ Koelman JM, Hoogerbrugge PJ (1993). "Динамическое моделирование подвесов твердых сфер при постоянном сдвиге". Письма Europhysics (EPL). 21 (3): 363–368. Bibcode:1993EL ..... 21..363K. Дои:10.1209/0295-5075/21/3/018. ISSN 0295-5075.
- ^ Español P, Уоррен P (1995). «Статистическая механика динамики диссипативных частиц». Письма Europhysics (EPL). 30 (4): 191–196. Bibcode:1995EL ..... 30..191E. Дои:10.1209/0295-5075/30/4/001. ISSN 0295-5075. S2CID 14385201.
- ^ Динамика диссипативных частиц: устранение недостатков и установление новых границ, Семинар CECAM, 16–18 июля 2008 г., Лозанна, Швейцария.
- ^ Коркут А., Хендриксон В.А. (сентябрь 2009 г.). «Силовое поле для виртуального атома молекулярной механики белков». Труды Национальной академии наук Соединенных Штатов Америки. 106 (37): 15667–72. Bibcode:2009PNAS..10615667K. Дои:10.1073 / pnas.0907674106. ЧВК 2734882. PMID 19717427.
- ^ Смит Дж. С., Исаев О., Ройтберг А. Э. (апрель 2017 г.). «АНИ-1: расширяемый потенциал нейронной сети с точностью DFT при стоимости вычислений силового поля». Химическая наука. 8 (4): 3192–3203. Дои:10.1039 / C6SC05720A. ЧВК 5414547. PMID 28507695.
- ^ Hughes ZE, Thacker JC, Wilson AL, Popelier PL (январь 2019 г.). «Описание потенциальных энергетических поверхностей молекул с использованием моделей машинного обучения FFLUX». Журнал химической теории и вычислений. 15 (1): 116–126. Дои:10.1021 / acs.jctc.8b00806. HDL:10454/16776. PMID 30507180.
- ^ Флетчер Т.Л., Папелье П.Л. (июнь 2016 г.). «Прогнозирование многополярной электростатической энергии для всех 20 природных аминокислот с использованием машинного обучения кригинга». Журнал химической теории и вычислений. 12 (6): 2742–51. Дои:10.1021 / acs.jctc.6b00457. PMID 27224739.
- ^ а б МакДонах Дж. Л., Сильва А. Ф., Винсент М. А., Попелье П. Л. (январь 2018 г.). «Машинное обучение динамических энергий корреляции электронов из топологических атомов». Журнал химической теории и вычислений. 14 (1): 216–224. Дои:10.1021 / acs.jctc.7b01157. PMID 29211469.
- ^ Рамакришнан Р., Драл П.О., Рупп М., фон Лилиенфельд О.А. (май 2015 г.). «Большие данные соответствуют приближениям квантовой химии: подход Δ-машинного обучения». Журнал химической теории и вычислений. 11 (5): 2087–96. arXiv:1503.04987. Bibcode:2015arXiv150304987R. Дои:10.1021 / acs.jctc.5b00099. PMID 26574412.
- ^ Schütt KT, Sauceda HE, Kindermans PJ, Tkatchenko A, Müller KR (июнь 2018 г.). «SchNet - Архитектура глубокого обучения для молекул и материалов». Журнал химической физики. 148 (24): 241722. arXiv:1712.06113. Bibcode:2018JChPh.148x1722S. Дои:10.1063/1.5019779. PMID 29960322. S2CID 4897444.
- ^ О. Т. Унке и М. Мьюли (2019). «PhysNet: нейронная сеть для прогнозирования энергии, сил, дипольных моментов и частичных зарядов». J. Chem. Тео. Chem. 15: 3678–3693 - через https://doi.org/10.1021/acs.jctc.9b00181.
- ^ Abascal JL, Vega C (декабрь 2005 г.). «Универсальная модель конденсированных фаз воды: TIP4P / 2005». Журнал химической физики. 123 (23): 234505. Bibcode:2005ЖЧФ.123w4505A. Дои:10.1063/1.2121687. PMID 16392929. S2CID 9757894.
- ^ Молинеро В., Мур Э.Б. (апрель 2009 г.). «Вода моделируется как промежуточный элемент между углеродом и кремнием». Журнал физической химии B. 113 (13): 4008–16. arXiv:0809.2811. Дои:10.1021 / jp805227c. PMID 18956896. S2CID 20782587.
- ^ Hughes ZE, Ren E, Thacker JC, Symons BC, Silva AF, Popelier PL (март 2020 г.). «Модель воды FFLUX: гибкая, поляризуемая и с многополярным описанием электростатики». Журнал вычислительной химии. 41 (7): 619–628. Дои:10.1002 / jcc.26111. ЧВК 7004022. PMID 31747059.
- ^ Хури Г.А., Томпсон Дж. П., Смадбек Дж., Кислич Калифорния, Флоудас Калифорния (декабрь 2013 г.). «Параметры Ab Initio Charge и AMBER Forcefield для часто встречающихся посттрансляционных модификаций». Журнал химической теории и вычислений. 9 (12): 5653–5674. Дои:10.1021 / ct400556v. ЧВК 3904396. PMID 24489522.
- ^ Хури Г.А., Смадбек Дж., Тамамис П., Вандрис А.С., Кислич Калифорния, Флоудас Калифорния (декабрь 2014 г.). «Forcefield_NCAA: параметры заряда ab initio для помощи в открытии и разработке терапевтических белков и пептидов с неприродными аминокислотами и их применении для дополнения ингибиторов семейства компстатина». Синтетическая биология ACS. 3 (12): 855–69. Дои:10.1021 / sb400168u. ЧВК 4277759. PMID 24932669.
- ^ Хури Г.А., Бхатия Н., Флоудас Калифорния (2014). «Энергия свободной гидратации, рассчитанная с использованием модели заряда AMBER ff03 для природных и неестественных аминокислот и нескольких моделей воды». Компьютеры и химическая инженерия. 71: 745–752. Дои:10.1016 / j.compchemeng.2014.07.017.
- ^ Дит Р.Дж. (2001). «Модель молекулярной механики поля лигандов и стереоэлектронные эффекты d- и s-электронов». Обзоры координационной химии. 212 (212): 11–34. Дои:10.1016 / S0010-8545 (00) 00354-4.
- ^ Фоскато М., Дит Р.Дж., Дженсен В.Р. (июнь 2015 г.). "Интеграция молекулярной механики поля лигандов в Tinker". Журнал химической информации и моделирования. 55 (6): 1282–90. Дои:10.1021 / acs.jcim.5b00098. PMID 25970002.
дальнейшее чтение
- Исраэлачвили Ю.Н. (1992). Межмолекулярные и поверхностные силы. Сан-Диего: Academic Press. ISBN 978-0-12-375181-2.
- Шлик Т. (2002). Молекулярное моделирование и симуляция: междисциплинарное руководство. Междисциплинарная прикладная математика: математическая биология. Нью-Йорк: Springer-Verlag. ISBN 978-0-387-95404-2.
- Варшел А (1991). Компьютерное моделирование химических реакций в ферментах и растворах. Нью-Йорк: Джон Вили и сыновья. ISBN 978-0-471-53395-5.