WikiDer > Оптическая передаточная функция

Иллюстрация оптической передаточной функции (OTF) и ее связи с качеством изображения. Оптическая передаточная функция хорошо сфокусированной (а) и расфокусированной оптической системы визуализации без аберраций (г). Поскольку оптическая передаточная функция этих систем является действительной и неотрицательной, оптическая передаточная функция по определению равна передаточной функции модуляции (ФПМ). Изображения точечного источника и говорил цель показаны на (b, e) и (c, f) соответственно. Обратите внимание, что масштаб точечных исходных изображений (b, e) в четыре раза меньше, чем целевых изображений спиц.

В оптическая передаточная функция (OTF) оптической системы, такой как камера, микроскоп, человеческий глаз, или же проектор определяет, как система обрабатывает различные пространственные частоты. Он используется инженерами-оптиками для описания того, как оптика проецирует свет от объекта или сцены на фотопленку. детекторная матрица, сетчатка, экран или просто следующий элемент в оптической цепочке передачи. Вариант, передаточная функция модуляции (МОГ), не учитывает фазовые эффекты, но во многих ситуациях эквивалентен OTF.

Либо функция передачи определяет ответ на периодический синусоидальная волна рисунок, проходящий через систему линз, в зависимости от его пространственной частоты или периода и его ориентации. Формально OTF определяется как преобразование Фурье из функция разброса точки (PSF, то есть импульсивный ответ оптики, изображение точечного источника). Как преобразование Фурье, OTF является комплексным; но он будет действительным в обычном случае PSF, симметричной относительно своего центра. MTF формально определяется как величина (абсолютное значение) сложной OTF.

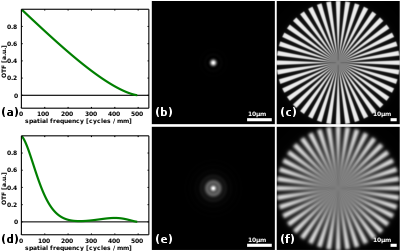
На изображении справа показаны функции оптического переноса для двух разных оптических систем на панелях (а) и (г). Первый соответствует идеалу, дифракционно ограниченный, система визуализации с круговой ученица. Его передаточная функция приблизительно постепенно уменьшается с пространственной частотой, пока не достигнет дифракционный предел, в данном случае при 500 циклах на миллиметр или периоде 2 мкм. Так как периодические особенности размером с этот период фиксируются этой системой визуализации, можно сказать, что ее разрешение составляет 2 мкм.^[1]. Панель (d) показывает оптическую систему, которая не в фокусе. Это приводит к резкому снижению контрастности по сравнению с дифракционно ограниченный система визуализации. Видно, что контраст равен нулю около 250 циклов / мм или периодов 4 мкм. Это объясняет, почему изображения для системы не в фокусе (e, f) более размыты, чем изображения для дифракционно ограниченный система (б, в). Обратите внимание, что хотя расфокусированная система имеет очень низкий контраст на пространственных частотах около 250 циклов / мм, контраст на пространственных частотах около дифракционного предела 500 циклов / мм ограничен дифракцией. Внимательное рассмотрение изображения на панели (f) показывает, что структура спиц относительно резкая для больших плотностей спиц около центра говорил цель.

Определение и связанные понятия

Поскольку оптическая передаточная функция^[2] (OTF) определяется как преобразование Фурье функции рассеяния точки (PSF), это вообще говоря комплексный функция пространственная частота. Проекция определенного периодического паттерна представлена ​​комплексным числом с абсолютным значением и сложный аргумент пропорционально относительному контрасту и переносу проецируемой проекции соответственно.

Различные тесно связанные характеристики оптической системы, демонстрирующие кому - типичную аберрацию, которая возникает вне оси. (а) Функция рассеяния точки (PSF) - это изображение точечного источника. (b) Изображение линии называется функцией растяжения линии, в данном случае вертикальной линией. Функция растяжения линии прямо пропорциональна вертикальной интеграции растянутого изображения. Функция оптической передачи (OTF) определяется как преобразование Фурье функции рассеяния точки и, таким образом, обычно является двумерной комплексной функцией. Обычно показан только одномерный срез (c), соответствующий преобразованию Фурье функции линейного расширения. Толстая зеленая линия указывает действительную часть функции, а тонкая красная линия - мнимую часть. Часто отображается только абсолютное значение комплексной функции, это позволяет визуализировать двумерную функцию (d); однако чаще показана только одномерная функция (e). Последняя обычно нормализуется на нулевой пространственной частоте и называется передаточной функцией модуляции (ФПМ). Для полноты картины сложный аргумент иногда предоставляется как функция передачи фазы (PhTF), показанная на панели (f).

Часто наибольший интерес представляет снижение контрастности, и перевод рисунка можно игнорировать. Относительный контраст определяется абсолютным значением оптической передаточной функции, функции, обычно называемой передаточная функция модуляции (МОГ). Его значения показывают, какая часть контраста объекта зафиксирована на изображении как функция пространственной частоты. MTF имеет тенденцию к уменьшению с увеличением пространственной частоты от 1 до 0 (на дифракционном пределе); однако функция часто не монотонный. С другой стороны, когда также важен перевод шаблона, сложный аргумент оптической передаточной функции можно изобразить как вторую действительную функцию, обычно называемую фазовая передаточная функция (PhTF). Комплексную оптическую передаточную функцию можно рассматривать как комбинацию этих двух действительных функций:

${displaystyle mathrm {OTF} (u) = mathrm {MTF} (u) e ^ {i, mathrm {PhTF} (u)}}$

куда

${displaystyle mathrm {MTF} (u) = leftvert mathrm {OTF} (u) ightvert,}$

${displaystyle mathrm {PhTF} (u) = mathrm {arg} (mathrm {OTF} (u)),}$

и ${displaystyle mathrm {arg} (cdot)}$ представляет функцию сложного аргумента, а ${displaystyle u}$ - пространственная частота периодического рисунка. В целом ${displaystyle u}$ - вектор с пространственной частотой для каждого измерения, то есть он также указывает направление периодического рисунка.

Импульсная характеристика хорошо сфокусированной оптической системы представляет собой трехмерное распределение интенсивности с максимумом в фокальной плоскости и, таким образом, может быть измерена путем записи стопки изображений при перемещении детектора в осевом направлении. Следовательно, трехмерная оптическая передаточная функция может быть определена как трехмерное преобразование Фурье импульсной характеристики. Хотя обычно используется только одномерный, а иногда и двухмерный разрез, трехмерная оптическая передаточная функция может улучшить понимание микроскопов, таких как микроскоп со структурированным освещением.

Верно определению функция передачи, ${displaystyle mathrm {OTF} (0) = mathrm {MTF} (0)}$ должен указывать долю света, который был обнаружен от объекта точечного источника. Однако, как правило, наиболее важен контраст по отношению к общему количеству обнаруженного света. Таким образом, обычной практикой является нормализация оптической передаточной функции к обнаруженной интенсивности, следовательно, ${displaystyle mathrm {MTF} (0) эквивалент 1}$.

Обычно оптическая передаточная функция зависит от таких факторов, как спектр и поляризация излучаемого света и положение точечного источника. Например. контраст и разрешение изображения обычно оптимальны в центре изображения и ухудшаются к краям поля зрения. Когда происходит значительное изменение, оптическая передаточная функция может быть рассчитана для набора репрезентативных положений или цветов.

Иногда более практично определять передаточные функции на основе двоичного рисунка черно-белых полос. Передаточная функция для черно-белого периодического рисунка одинаковой ширины называется функция передачи контраста (CTF).^[3]

Примеры

OTF идеальной системы линз

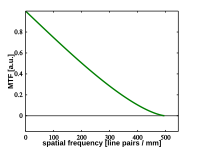
Идеальная система линз обеспечит высококонтрастную проекцию без смещения периодического рисунка, поэтому оптическая передаточная функция идентична передаточной функции модуляции. Обычно контраст постепенно уменьшается до нуля в точке, определяемой разрешением оптики. Например, идеальный, неаберрированный, f / 4 Используемая оптическая система формирования изображения на длине волны видимого света 500 нм будет иметь оптическую передаточную функцию, изображенную на правом рисунке.

Одномерная оптическая передаточная функция системы формирования изображений с дифракционным ограничением идентична ее передаточной функции модуляции.

Обозначенная цель, отображаемая системой визуализации с ограничением дифракции.

Передаточная функция и пример изображения идеальной системы визуализации без оптических аберраций (с ограничением дифракции).

Из графика видно, что контраст постепенно уменьшается и достигает нуля при пространственной частоте 500 циклов на миллиметр, другими словами, оптическое разрешение проекции изображения составляет 1/500.^th миллиметра или 2 микрометра. Соответственно, для этого конкретного устройства формирования изображения спицы становятся все более и более размытыми по направлению к центру, пока они не сливаются в серый неразрешенный диск. Обратите внимание, что иногда оптическая передаточная функция задается в единицах измерения объекта или пространства образца, угла наблюдения, ширины пленки или нормирована на теоретический максимум. Преобразование между ними обычно происходит путем умножения или деления. Например. микроскоп обычно увеличивает все от 10 до 100 раз, а зеркальная камера, как правило, уменьшает увеличение объектов на расстоянии 5 метров в 100-200 раз.

Разрешение устройства цифровой обработки изображений ограничено не только оптикой, но и количеством пикселей, в частности, расстоянием между ними. Как объяснил Теорема выборки Найквиста – Шеннона, чтобы соответствовать оптическому разрешению данного примера, пиксели каждого цветового канала должны быть разделены на 1 микрометр, половину периода 500 циклов на миллиметр. Большее количество пикселей на датчике того же размера не позволит получить более мелкие детали. С другой стороны, когда расстояние между пикселями больше 1 микрометра, разрешение будет ограничено расстоянием между пикселями; более того, сглаживание может привести к дальнейшему снижению точности изображения.

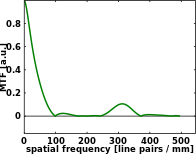
OTF несовершенной линзовой системы

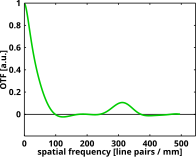
Несовершенный, аберрированный Система визуализации может обладать оптической передаточной функцией, изображенной на следующем рисунке.

Реальная часть оптической передаточной функции аберрированной несовершенной системы визуализации.

Функция передачи модуляции аберрированной, несовершенной системы визуализации.

Изображение спицы-мишени, полученное аберрированной оптической системой.

Передаточная функция и пример изображения оптической системы формирования изображения f / 4 на 500 нм со сферической аберрацией со стандартным коэффициентом Цернике 0,25.

В идеальной системе линз контраст достигает нуля при пространственной частоте 500 циклов на миллиметр. Однако на более низких пространственных частотах контраст значительно ниже, чем у совершенной системы в предыдущем примере. Фактически, контраст становится равным нулю в нескольких случаях даже для пространственных частот ниже 500 циклов на миллиметр. Это объясняет серые круглые полосы на изображении спиц, показанном на приведенном выше рисунке. Между серыми полосами спицы меняют цвет с черного на белый и наоборот, это называется инверсией контраста, напрямую связанной с изменением знака в действительной части оптической передаточной функции, и представляет собой сдвиг на половину периода для некоторых периодических шаблонов.

Хотя можно утверждать, что разрешение как идеальной, так и несовершенной системы составляет 2 мкм, или 500 LP / мм, очевидно, что изображения в последнем примере менее резкие. Определение разрешения, которое больше соответствует воспринимаемому качеству, вместо этого будет использовать пространственную частоту, на которой происходит первый ноль, 10 мкм или 100 LP / мм. Определения разрешения даже для идеальных систем визуализации сильно различаются. Более полную однозначную картину дает оптическая передаточная функция.

OTF оптической системы с не вращательной симметричной аберрацией

При просмотре через оптическую систему с аберрацией трилистника изображение точечного объекта будет выглядеть как трехконечная звезда (а). Поскольку функция рассеяния точки не является вращательно-симметричной, только двумерная оптическая передаточная функция может хорошо ее описать (b). Высота графика поверхности указывает абсолютное значение, а оттенок указывает сложный аргумент функции. Спица-мишень, отображаемая таким устройством формирования изображения, показана при моделировании в (c).

Оптические системы, в частности оптические аберрации не всегда осесимметричны. Таким образом, периодические узоры с разной ориентацией могут отображаться с разным контрастом, даже если их периодичность одинакова. Таким образом, оптическая передаточная функция или передаточные функции модуляции обычно являются двумерными функциями. На следующих рисунках показан двумерный эквивалент идеальной и несовершенной системы, обсужденных ранее, для оптической системы с трилистник, не вращательно-симметричная аберрация.

Оптические передаточные функции не всегда являются действительными. Шаблоны периода могут быть сдвинуты на любую величину, в зависимости от аберрации в системе. Обычно это происходит с неосимметричными аберрациями. Оттенок цветов участков поверхности на рисунке выше указывает фазу. Можно видеть, что в то время как для вращательно-симметричных аберраций фаза равна 0 или π и, таким образом, передаточная функция является действительной, для не вращательно-симметричной аберрации передаточная функция имеет мнимую составляющую, и фаза изменяется непрерывно.

Практический пример - видеосистема высокого разрешения

Пока оптическое разрешение, как обычно используется применительно к системам камер, описывает только количество пикселей в изображении и, следовательно, возможность показать мелкие детали, передаточная функция описывает способность соседних пикселей изменяться с черного на белый в ответ на шаблоны изменения пространственная частота и, следовательно, реальная способность отображать мелкие детали, будь то с полным или уменьшенным контрастом. Изображение, воспроизводимое с помощью функции оптической передачи, которая «скатывается» на высоких пространственных частотах, будет казаться «размытым» на повседневном языке.

На примере современной видеосистемы высокой четкости (HD) с разрешением 1920 на 1080 пикселей Теорема Найквиста утверждает, что в идеальной системе должно быть возможно полностью разрешить (с истинными переходами от черного к белому) в общей сложности 1920 комбинированных чередующихся черных и белых линий, иначе называемых пространственной частотой 1920/2 = 960 пар линий на ширина изображения, или 960 циклов на ширину изображения (также возможны определения в терминах циклов на единицу угла или на мм, но, как правило, менее четкие при работе с камерами и более подходят для телескопов и т. д.). На практике это далеко не так, и пространственные частоты, приближающиеся к Курс Найквиста обычно воспроизводятся с уменьшающейся амплитудой, поэтому мелкие детали, хотя их можно увидеть, значительно уменьшаются по контрасту. Это приводит к интересному наблюдению, что, например, телевизионное изображение стандартной четкости, полученное с помощью пленочного сканера, который использует передискретизация, как описано ниже, может казаться более резким, чем изображение высокой четкости, снятое камерой с плохой функцией передачи модуляции. Эти два изображения демонстрируют интересную разницу, которую часто упускают из виду: первая имеет полный контраст деталей до определенного момента, но затем не имеет действительно мелких деталей, в то время как вторая действительно содержит более мелкие детали, но с таким уменьшенным контрастом, что в целом выглядит хуже.

Трехмерная оптическая передаточная функция

Трехмерные функции рассеяния точки (a, c) и соответствующие функции передачи модуляции (b, d) широкоугольного микроскопа (a, b) и конфокального микроскопа (c, d). В обоих случаях числовая апертура объектива составляет 1,49, а показатель преломления среды 1,52. Предполагается, что длина волны излучаемого света составляет 600 нм, а в случае конфокального микроскопа длина волны возбуждающего света составляет 500 нм с круговой поляризацией. Раздел вырезается для визуализации внутреннего распределения интенсивности. Цвета, показанные на логарифмической цветовой шкале, указывают на освещенность (a, c) и спектральную плотность (b, d), нормированные на максимальное значение.

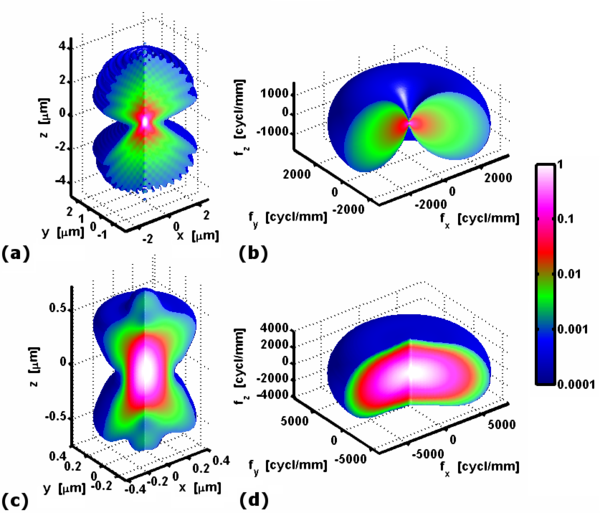
Хотя обычно изображение воспринимается как плоское или двухмерное, система формирования изображения создает трехмерное распределение интенсивности в пространстве изображения, которое в принципе можно измерить. например Двумерный датчик можно преобразовать в трехмерное распределение интенсивности. Изображение точечного источника также представляет собой трехмерное (3D) распределение интенсивности, которое может быть представлено функцией трехмерного рассеяния точки. В качестве примера на рисунке справа показана трехмерная функция рассеяния точки в пространстве объекта широкоугольного микроскопа (а) наряду с функцией конфокального микроскопа (с). Хотя используется тот же объектив микроскопа с числовой апертурой 1,49, ясно, что функция рассеяния конфокальной точки более компактна как по боковым размерам (x, y), так и по осевым размерам (z). Можно было бы справедливо заключить, что разрешение конфокального микроскопа превосходит разрешение широкоугольного микроскопа во всех трех измерениях.

Трехмерная оптическая передаточная функция может быть вычислена как трехмерное преобразование Фурье трехмерной функции рассеяния точки. Его величина с цветовой кодировкой показана на панелях (b) и (d), что соответствует функциям распределения точки, показанным на панелях (a) и (c), соответственно. Передаточная функция широкоугольного микроскопа имеет поддерживать это половина разрешения конфокального микроскопа во всех трех измерениях, что подтверждает ранее отмеченное более низкое разрешение широкоугольного микроскопа. Обратите внимание, что вдоль zось, для Икс = у = 0, передаточная функция равна нулю везде, кроме начала координат. Этот отсутствующий конус это хорошо известная проблема, которая препятствует оптическому сечению с использованием широкопольного микроскопа.^[4]

Двумерная оптическая передаточная функция в фокальной плоскости может быть рассчитана путем интегрирования трехмерной оптической передаточной функции вдоль z-ось. Хотя передаточная функция 3D широкоугольного микроскопа (b) равна нулю на z-ось для z ≠ 0; его интеграл, двумерный оптический перенос, достигающий максимума при Икс = у = 0. Это возможно только потому, что трехмерная оптическая передаточная функция расходится в начале координат. Икс = у = z = 0. Значения функции вдоль z-оси оптической передаточной функции 3D соответствуют Дельта-функция Дирака.

Расчет

Наиболее программное обеспечение для оптического дизайна имеет функциональные возможности для вычисления оптической функции или функции передачи модуляции конструкции линзы. Идеальные системы, такие как в приведенных здесь примерах, легко рассчитываются численно с использованием такого программного обеспечения, как Юля, GNU Octave или же Matlab, а в некоторых конкретных случаях даже аналитически. Оптическую передаточную функцию можно рассчитать двумя способами:^[5]

1. как преобразование Фурье некогерентного функция разброса точки, или же
2. как автокорреляция функция зрачка оптической системы

Математически оба подхода эквивалентны. Числовые вычисления обычно наиболее эффективно выполняются с помощью преобразования Фурье; однако аналитический расчет может быть более управляемым с использованием подхода автокорреляции.

Пример

Идеальная система линз с круглой апертурой

Автокорреляция функции зрачка

Поскольку оптическая передаточная функция преобразование Фурье из функция разброса точки, а функция рассеяния точки - это абсолютный квадрат обратного преобразования Фурье. функция зрачка, оптическую передаточную функцию также можно рассчитать непосредственно из функция зрачка. От теорема свертки видно, что оптическая передаточная функция на самом деле автокорреляция из функция зрачка.^[5]

Функция зрачка идеальной оптической системы с круглой апертурой - это диск единичного радиуса. Таким образом, оптическая передаточная функция такой системы может быть рассчитана геометрически по площади пересечения двух идентичных дисков на расстоянии ${displaystyle 2u}$, куда ${displaystyle u}$ - пространственная частота, нормализованная к самой высокой передаваемой частоте.^[2] Обычно оптическая передаточная функция нормируется на максимальное значение, равное единице для ${displaystyle u = 0}$, поэтому полученную площадь нужно разделить на ${displaystyle pi}$.

Площадь пересечения можно рассчитать как сумму площадей двух одинаковых круглые сегменты: ${displaystyle heta / 2-sin (heta) / 2}$, куда ${displaystyle heta}$ - угол сегмента круга. Подставив ${displaystyle | u | = cos (heta / 2)}$, и используя равенства ${displaystyle sin (heta) / 2 = sin (heta / 2) cos (heta / 2)}$ и ${displaystyle 1 = u ^ {2} + sin (arccos (| u |)) ^ {2}}$, уравнение для площади можно переписать в виде ${displaystyle arccos (| u |) - | u | {sqrt {1-u ^ {2}}}}$. Следовательно, нормализованная оптическая передаточная функция определяется выражением:

${displaystyle operatorname {OTF} (u) = {frac {2} {pi}} left (arccos (| u |) - | u | {sqrt {1-u ^ {2}}} ight).}$

Более подробное обсуждение можно найти в ^[5] и.^{[2]:152–153}

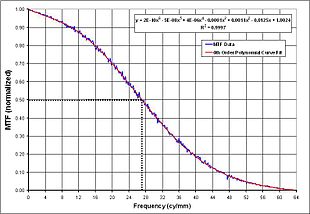
Числовая оценка

Одномерная оптическая передаточная функция может быть рассчитана как дискретное преобразование Фурье функции растяжения линии. Эти данные нанесены на график пространственная частота данные. В этом случае полином шестого порядка аппроксимируется MTF против пространственной частоты кривая, чтобы показать тенденцию. Частота среза 50% определяется для получения соответствующей пространственной частоты. Таким образом, примерное положение наилучшего фокуса тестируемый блок определяется из этих данных.

В МОГ данные в зависимости от пространственной частоты нормализуются путем подгонки к ним полинома шестого порядка, создавая плавную кривую. Определяется частота среза 50% и соответствующий пространственная частота находится, что дает примерное положение лучший фокус.

Преобразование Фурье функции рассеяния линии (LSF) не может быть определено аналитически с помощью следующих уравнений:

${displaystyle operatorname {MTF} = {mathcal {F}} left [operatorname {LSF} ight] qquad имя оператора qquad {MTF} = int f (x) e ^ {- i2pi, xs}, dx}$

Следовательно, преобразование Фурье численно аппроксимируется с использованием дискретного преобразования Фурье. ${displaystyle {mathcal {DFT}}}$.^[6]

${displaystyle operatorname {MTF} = {mathcal {DFT}} [operatorname {LSF}] = Y_ {k} = sum _ {n = 0} ^ {N-1} y_ {n} e ^ {- ik {frac { 2pi} {N}} n} qquad kin [0, N-1]}$

куда

• ${displaystyle Y_ {k},}$ = the ${displaystyle k ^ {ext {th}}}$ значение MTF
• ${displaystyle N,}$ = количество точек данных
• ${displaystyle n,}$ = индекс
• ${displaystyle k,}$ = ${displaystyle k ^ {ext {th}}}$ срок данных LSF
• ${displaystyle y_ {n},}$ = ${displaystyle n ^ {ext {th}},}$ позиция пикселя
• ${displaystyle i = {sqrt {-1}}}$

${displaystyle e ^ {pm ia} = cos (a), pm, isin (a)}$

${displaystyle operatorname {MTF} = {mathcal {DFT}} [operatorname {LSF}] = Y_ {k} = sum _ {n = 0} ^ {N-1} y_ {n} left [cos left (k {frac {2pi} {N}} ночь) -isin left (k {frac {2pi} {N}} night) ight] qquad kin [0, N-1]}$

Затем MTF наносится на график в зависимости от пространственной частоты, и все соответствующие данные, касающиеся этого теста, могут быть определены на этом графике.

Векторная передаточная функция

При высоких числовых апертурах, например, в микроскопии, важно учитывать векторную природу полей, переносящих свет. Разложив волны на три независимых компонента, соответствующих декартовым осям, можно вычислить функцию рассеяния точки для каждого компонента и объединить ее в векторный функция разброса точки. Аналогично векторный оптическую передаточную функцию можно определить, как показано на (^[7]) и (^[8]).

Измерение

Функция оптического переноса полезна не только для проектирования оптических систем, но и для характеристики производимых систем.

Начиная с функции распределения точки

Оптическая передаточная функция определяется как преобразование Фурье из импульсивный ответ оптической системы, также называемой функция разброса точки. Таким образом, оптическую передаточную функцию легко получить, сначала получив изображение точечного источника, и применив двумерный дискретное преобразование Фурье к образцу изображения. Таким точечным источником может быть, например, яркий свет за экраном с точечным отверстием, люминесцентный или металлический микросфера, или просто точка, нарисованная на экране. Расчет оптической передаточной функции с помощью функции рассеяния точки является универсальным, поскольку он может полностью охарактеризовать оптику с пространственными изменениями и хроматическими аберрациями, повторяя процедуру для различных положений и спектров длин волн точечного источника.

Использование расширенных тестовых объектов для пространственно-инвариантной оптики

Когда можно предположить, что аберрации пространственно инвариантны, можно использовать альтернативные шаблоны для определения оптической передаточной функции, например линий и краев. Соответствующие передаточные функции называются функцией расширения строки и функцией расширения границы соответственно. Такие протяженные объекты освещают большее количество пикселей изображения и могут повысить точность измерения за счет большего отношения сигнал / шум. Оптическая передаточная функция в этом случае вычисляется как двумерная дискретное преобразование Фурье изображения и делится на расширенный объект. Обычно используется либо линия, либо черно-белый край.

Функция линейного расширения

Двумерное преобразование Фурье линии, проходящей через начало координат, - это прямая, ортогональная ей и проходящая через начало координат. Таким образом, делитель равен нулю для всех измерений, кроме одного, следовательно, оптическая передаточная функция может быть определена только для одного измерения с использованием одного функция растяжения линии (LSF). При необходимости двумерная оптическая передаточная функция может быть определена путем повторения измерения с линиями под разными углами.

Функцию растяжения линии можно найти двумя разными способами. Его можно найти непосредственно из приближения идеальной линии, обеспечиваемого щелевой тестовой мишенью, или его можно получить из функции расширения границ, обсуждаемой в следующем подразделе.

Функция расширения кромки

Двумерное преобразование Фурье ребра также отлично от нуля только на одной прямой, ортогональной ребру. Эту функцию иногда называют функция расширения края (ESF).^[9][10] Однако значения в этой строке обратно пропорциональны расстоянию от начала координат. Хотя изображения измерений, полученные с помощью этого метода, освещают большую часть камеры, это в основном улучшает точность на низких пространственных частотах. Как и в случае функции рассеяния линии, каждое измерение определяет только одну ось оптической передаточной функции, поэтому необходимы повторные измерения, если оптическая система не может считаться осесимметричной.

При оценке ESF, оператор определяет площадь прямоугольника, эквивалентную 10%^{[нужна цитата]} от общей площади кадра острие испытательной мишени с задней подсветкой черное тело. Область определяется так, чтобы охватить край целевого изображения.

Как показано на правом рисунке, оператор определяет область прямоугольника, охватывающую край острие испытательной мишени изображение с задней подсветкой черное тело. Площадь коробки определена как приблизительно 10%^{[нужна цитата]} от общей площади кадра. Изображение пиксель данные преобразуются в двумерный массив (пиксель интенсивность и положение пикселя). Амплитуда (интенсивность пикселей) каждого линия в массиве нормализованный и в среднем. Это дает функцию расширения края.

${displaystyle operatorname {ESF} = {frac {X-mu} {sigma}} qquad qquad sigma, = {sqrt {frac {sum _ {i = 0} ^ {n-1} (x_ {i} -mu,) ^ {2}} {n}}} qquad qquad mu, = {frac {sum _ {i = 0} ^ {n-1} x_ {i}} {n}}}$

куда

• ESF = выходной массив нормализованных данных интенсивности пикселей
• ${displaystyle X,}$ = входной массив данных интенсивности пикселей
• ${displaystyle x_ {i},}$ = the я^th элемент ${displaystyle X,}$
• ${displaystyle mu,}$ = среднее значение данных интенсивности пикселей
• ${displaystyle sigma,}$ = стандартное отклонение данных интенсивности пикселей
• ${displaystyle n,}$ = количество пикселей, используемых в среднем

Функция растяжения линии идентична функции первая производная функции расширения края,^[11] который дифференцируется с помощью численные методы. В случае, если более практично измерить функцию размытия края, можно определить функцию размытия линии следующим образом:

${displaystyle operatorname {LSF} = {frac {d} {dx}} operatorname {ESF} (x)}$

Обычно ESF известен только в дискретных точках, поэтому LSF численно аппроксимируется с использованием конечная разница:

${displaystyle operatorname {LSF} = {frac {d} {dx}} operatorname {ESF} (x) приблизительно {frac {Delta operatorname {ESF}} {Delta x}}}$

${displaystyle operatorname {LSF} приблизительно {frac {operatorname {ESF} _ {i + 1} -operatorname {ESF} _ {i-1}} {2 (x_ {i + 1} -x_ {i})}}}$

куда:

• ${displaystyle i,}$ = индекс ${displaystyle i = 1,2, dots, n-1}$
• ${displaystyle x_ {i},}$ = ${displaystyle i ^ {ext {th}},}$ позиция ${displaystyle i ^ {ext {th}},}$ пиксель
• ${displaystyle operatorname {ESF} _ {i},}$ = ESF ${displaystyle i ^ {ext {th}},}$ пиксель

Использование сетки из черных и белых линий

Хотя «резкость» часто оценивается по сетке из чередующихся черных и белых линий, ее следует строго измерять с использованием синусоидального изменения от черного к белому (размытая версия обычного рисунка). При использовании прямоугольной волны (простые черные и белые линии) не только повышается риск появления наложения спектров, но и необходимо учитывать тот факт, что основная составляющая прямоугольной волны выше, чем амплитуда самой прямоугольной волны ( гармонические составляющие уменьшают пиковую амплитуду). Таким образом, тестовая диаграмма с прямоугольной волной будет показывать оптимистичные результаты (лучшее разрешение высоких пространственных частот, чем фактически достигается). Результат прямоугольной волны иногда называют «функцией передачи контраста» (CTF).

Факторы, влияющие на MTF в типичных системах камер

На практике многие факторы приводят к значительному размытию воспроизводимого изображения, так что шаблоны с пространственной частотой чуть ниже Курс Найквиста могут быть даже не видны, а тончайшие узоры могут казаться «размытыми» в виде оттенков серого, а не черного и белого. Основным фактором обычно является невозможность создать идеальный оптический фильтр «кирпичная стена» (часто реализуемый какфазовая пластина'или объектив с особыми свойствами размытия в цифровых фотоаппаратах и ​​видеокамерах). Такой фильтр необходим для уменьшения сглаживание устраняя пространственные частоты выше Курс Найквиста дисплея.

Передискретизация и понижающее преобразование для поддержания функции оптической передачи

Единственный практический способ приблизиться к теоретической резкости, возможной в системе цифровой обработки изображений, такой как камера, - это использовать больше пикселей в датчике камеры, чем образцы в окончательном изображении и «преобразовать с понижением частоты» или «интерполировать» с помощью специальной цифровой обработки, которая отсекает высокие частоты выше Курс Найквиста чтобы избежать наложения спектров при сохранении достаточно плоского MTF до этой частоты. Этот подход был впервые применен в 1970-х годах при использовании точечных сканеров, а позже CCD Были разработаны линейные сканеры, которые отбирали больше пикселей, чем требовалось, а затем преобразовывали их с понижением частоты, поэтому фильмы на телевидении всегда выглядели резче, чем другие материалы, снятые с помощью видеокамеры. Единственный теоретически правильный способ интерполировать или преобразовать с понижением частоты - использовать крутой пространственный фильтр нижних частот, реализованный свертка с двумерным грехом (Икс)/Икс взвешивание функция, требующая мощной обработки. На практике для уменьшения требований к обработке используются различные математические приближения. Эти приближения теперь широко применяются в системах редактирования видео и в программах обработки изображений, таких как Фотошоп.

Подобно тому, как видео стандартной четкости с высококонтрастным MTF возможно только с передискретизацией, телевидение высокой четкости с полной теоретической резкостью возможно только при использовании камеры со значительно более высоким разрешением с последующей цифровой фильтрацией. Сейчас снимают фильмы. 4k и даже видео 8k для кино, мы можем ожидать увидеть лучшие изображения на HDTV только из фильмов или материалов, снятых по более высоким стандартам. Как бы мы ни увеличивали количество пикселей, используемых в камерах, это всегда будет оставаться верным при отсутствии идеального оптического пространственного фильтра. Точно так же 5-мегапиксельное изображение, полученное с 5-мегапиксельной фотокамеры, никогда не может быть четче, чем 5-мегапиксельное изображение, полученное после понижающего преобразования от 10-мегапиксельной фотокамеры того же качества. Из-за проблемы с поддержанием высокой контрастности MTF вещатели, такие как BBC долгое время рассматривал возможность сохранения телевидения стандартной четкости, но улучшения его качества за счет съемки и просмотра с большим количеством пикселей (хотя, как уже упоминалось ранее, такая система, хотя и впечатляет, в конечном итоге не хватает очень мелких деталей, которые, хотя и ослаблены, улучшают эффект истинного просмотра HD).

Еще одним фактором цифровых фотоаппаратов и видеокамер является разрешение объектива. Можно сказать, что объектив «разрешает» 1920 горизонтальных линий, но это не означает, что он делает это с полной модуляцией от черного к белому. «Функция передачи модуляции» (просто термин для величины оптической передаточной функции без учета фазы) дает истинную меру характеристик линзы и представлена ​​графиком зависимости амплитуды от пространственной частоты.

Дифракция на апертуре объектива также ограничивает MTF. Хотя уменьшение диафрагмы объектива обычно уменьшает аберрации и, следовательно, улучшает плоскостность MTF, существует оптимальная диафрагма для любого размера объектива и датчика изображения, за пределами которой меньшая диафрагма снижает разрешение из-за дифракции, которая распространяет свет по датчику изображения. Во времена плоских фотоаппаратов и даже 35-миллиметровой пленки это не было проблемой, но стало непреодолимым ограничением из-за очень маленьких датчиков формата, используемых в некоторых цифровых камерах и особенно видеокамерах. В бытовых видеокамерах HD первого поколения использовались 1/4-дюймовые сенсоры, для которых диафрагма меньше примерно f4 начинает ограничивать разрешение. Даже профессиональные видеокамеры в основном используют сенсоры размером 2/3 дюйма, что запрещает использование диафрагмы около f16, что считалось бы нормальным для форматов пленки. Некоторые камеры (например, Pentax K10D) есть режим «Автоэкспозиция MTF», в котором выбор диафрагмы оптимизирован для максимальной резкости. Обычно это означает где-то в середине диапазона диафрагмы.^[12]

Тенденция к широкоформатным зеркальным фотокамерам и улучшенный потенциал MTF

Недавно произошел сдвиг в сторону использования большого формата изображений. цифровые однообъективные зеркальные фотоаппараты движимый потребностью в низкой освещенности и узком глубина резкости последствия. Это привело к тому, что некоторые производители фильмов и телевизионных программ предпочитают такие камеры даже профессиональным видеокамерам HD из-за их «кинематографического» потенциала. Теоретически использование камер с сенсорами на 16 и 21 мегапикселей дает возможность получить почти идеальную резкость за счет понижающего преобразования внутри камеры с цифровой фильтрацией для устранения наложения спектров. Такие камеры дают очень впечатляющие результаты и, по-видимому, лидируют в производстве видео по направлению к понижающему преобразованию большого формата, при этом цифровая фильтрация становится стандартным подходом к реализации плоского MTF с истинной свободой от наложения спектров.

Цифровая инверсия оптической передаточной функции

Из-за оптических эффектов контраст может быть неоптимальным и приближается к нулю до Частота Найквиста дисплея. Уменьшение оптического контраста может быть частично отменено путем выборочного цифрового усиления пространственных частот перед отображением или дальнейшей обработкой. Хотя более продвинутый цифровой восстановление изображения существуют процедуры, Винеровская деконволюция алгоритм часто используется из-за его простоты и эффективности. Поскольку этот метод умножает пространственные спектральные компоненты изображения, он также усиливает шум и ошибки, например, из-за алиасинг. Поэтому он эффективен только при записи хорошего качества с достаточно высоким отношением сигнал / шум.

Ограничения

В целом функция разброса точки, изображение точечного источника также зависит от таких факторов, как длина волны (цвет), и поле угол (положение источника боковой точки). Когда такое изменение достаточно плавное, оптическая система может быть охарактеризована набором оптических передаточных функций. Однако, когда изображение точечного источника резко изменяется при боковом перемещении, оптическая передаточная функция не описывает точно оптическую систему.

Смотрите также

• Боке
• Гамма-коррекция
• Минимальный разрешаемый контраст
• Минимальная разрешаемая разница температур
• Оптическое разрешение
• Соотношение сигнал шум
• Функция передачи сигнала
• Коэффициент Штреля
• Функция передачи
• Кодирование волнового фронта

Рекомендации

внешняя ссылка

• «Передаточная функция модуляции», Гленн Д. Бореман на SPIE Optipedia.
• «Как измерить MTF и другие свойства линз», компанией Optikos Corporation.