WikiDer > Группы точек в четырех измерениях

Иерархия четырехмерных полихорических точечных групп и некоторых подгрупп. Вертикальное позиционирование сгруппировано по порядку. Синий, зеленый и розовый цвета показывают группы отражений, гибридов и вращения.

Некоторые четырехмерные точечные группы в обозначениях Конвея

В геометрия, а точечная группа в четырех измерениях является группа изометрии в четырех измерениях, которые оставляют начало координат фиксированным, или, соответственно, группу изометрий 3-сфера.

История четырехмерных групп

• 1889 Эдуард Гурса, О ортогональных заменах и правилах разделов пространства, Annales Scientifiques de l'École Normale Supérieure, Sér. 3, 6, (стр. 9–102, стр. 80–81 тетраэдры), Тетраэдр Гурса
• 1951, А. К. Херли, Конечные группы вращения и классы кристаллов в четырех измерениях, Труды Кембриджского философского общества, вып. 47, выпуск 04, с. 650^[1]
• 1962 А. Л. Маккей Решетки Браве в четырехмерном пространстве^[2]
• 1964 Патрик дю Валь, Гомографии, кватернионы и вращения, кватернионгруппы точек 4D
• 1975 Ян Мозжимас, Анджей Солецкий, Группы точек R4, Доклады по математической физике, Том 7, Выпуск 3, с. 363-394 ^[3]
• 1978 Х. Браун, Р. Бюлов, Й. Нойбюзер, Х. Вондрачек и Х. Цассенхаус, Кристаллографические группы четырехмерного пространства.^[4]
• 1982 Н. П. Уорнер, Группы симметрии регулярных мозаик S2 и S3 ^[5]
• 1985 Э. ​​Дж. Уиттакер, Атлас гиперстереограмм четырехмерные кристаллические классы
• 1985 H.S.M. Coxeter, Правильные и полурегулярные многогранники II, Обозначения Кокстера для 4D точечных групп
• 2003 Джон Конвей и Смит, О кватернионах и октонионах, Завершенный кватернионгруппы точек 4D
• 2018 Н. В. Джонсон Геометрии и преобразования, Глава 11,12,13, Полные полихорические группы, с.249, дуопризматические группы с.269

Изометрии точечной симметрии 4D

Существует четыре основных изометрии 4-мерного точечная симметрия: симметрия отражения, вращательная симметрия, вращательное отражение, и двойное вращение.

Обозначения для групп

Группы точек в этой статье приведены в Обозначение Кокстера, которые основаны на Группы Кокстера, с пометками для расширенных групп и подгрупп.^[6] Обозначения Кокстера имеют прямое соответствие диаграмме Кокстера, например [3,3,3], [4,3,3], [3^1,1,1], [3,4,3], [5,3,3] и [p, 2, q]. Эти группы связывают 3-сфера на одинаковые гиперсферические тетраэдрические области. Количество доменов - это порядок группы. Количество зеркал для неприводимой группы равно нч / 2, куда час группа Кокстера Число Кокстера, п - размерность (4).^[7]

Для перекрестных ссылок здесь также приведены кватернион основанные на обозначениях Патрик дю Валь (1964)^[8] и Джон Конвей (2003).^[9] Обозначения Конвея позволяют вычислить порядок группы как произведение элементов с порядками групп киральных полиэдров: (T = 12, O = 24, I = 60). В обозначениях Конвея префикс (±) означает центральная инверсия, а суффикс (.2) означает зеркальную симметрию. Точно так же в нотации Дюваля есть надстрочный знак звездочки (*) для зеркальной симметрии.

Группы инволюции

Есть пять инволюционный группы: без симметрии []⁺, симметрия отражения [], 2-кратный вращательная симметрия [2]⁺, 2-кратный вращательное отражение [2⁺,2⁺] и центральный точечная симметрия [2⁺,2⁺,2⁺] как 2-кратное двойное вращение.

Группы Кокстера 4 ранга

А полихорическая группа один из пяти группы симметрии 4-х мерного правильные многогранники. Есть также три полиэдральных призматических группы и бесконечное множество дуопризматических групп. Каждая группа определяется Тетраэдр Гурса фундаментальная область ограничен зеркальными плоскостями. В двугранные углы между зеркалами определить порядок двугранная симметрия. В Диаграмма Кокстера – Дынкина - это граф, в котором узлы представляют собой зеркальные плоскости, а ребра называются ветвями и обозначаются порядком двугранного угла между зеркалами.

Период, термин полихорон (множественное число полихора, прилагательное полихорический), от Греческий корни поли («многие») и хоро («комната» или «пространство») и рекомендуется^[10] к Норман Джонсон и Георгий Ольшевский в контексте однородная полихора (4-многогранники) и связанные с ними 4-мерные группы симметрии.^[11]

4 место Группы Кокстера позволяет комплекту из 4 зеркал покрывать 4 пространства и разделяет 3-сфера на тетраэдрические фундаментальные области. Группы Кокстера нижнего ранга могут ограничивать только осоэдр или же гозотоп фундаментальные области на трехмерной сфере.

Как 3D многогранные группы, имена заданных четырехмерных полихорических групп построены из греческих префиксов подсчетов клеток соответствующих треугольных правильных многогранников.^[12] Расширенная симметрия существует в однородных полихорах с симметричными кольцевыми узорами внутри Диаграмма Кокстера построить. Киральные симметрии существуют в чередовались однородная полихора.

Только неприводимые группы имеют числа Кокстера, но дуопризматические группы [p, 2, p] могут быть удвоены до [[p, 2, p]] путем добавления 2-кратной инерции к фундаментальной области, и это дает эффективное число Кокстера 2п, например [4,2,4] и его полная симметрия B₄, [4,3,3] группа с числом Кокстера 8.

Weyl группа	Конвей Кватернион	Абстрактный структура	Coxeter диаграмма		Coxeter обозначение	Заказ	Коммутатор подгруппа	Coxeter номер (час)	Зеркала (м)
Полные полихорические группы
А4	+1/60 [I × I] .21	S5			[3,3,3]	120	[3,3,3]+	5		10
D4	± 1/3 [Т × Т] .2	1/2.2S4			[31,1,1]	192	[31,1,1]+	6		12
B4	± 1/6 [O × O] .2	2S4 = S2≀S4			[4,3,3]	384		8	4	12
F4	± 1/2 [O × O] .23	3.2S4			[3,4,3]	1152	[3+,4,3+]	12	12	12
ЧАС4	± [I × I] .2	2. (А5× А5).2			[5,3,3]	14400	[5,3,3]+	30		60
Полные многогранные призматические группы
А3А1	+1/24 [O × O] .23	S4× D1			[3,3,2] = [3,3]×[ ]	48	[3,3]+	-		6	1
B3А1	± 1/24 [O × O] .2	S4× D1			[4,3,2] = [4,3]×[ ]	96		-	3	6	1
ЧАС3А1	± 1/60 [I × I] .2	А5× D1			[5,3,2] = [5,3]×[ ]	240	[5,3]+	-		15	1
Полные дуопризматические группы
4А1 = 2D2	± 1/2 [D4× D4]	D14 = D22			[2,2,2] = [ ]4 = [2]2	16	[ ]+	4	1	1	1	1
D2B2	± 1/2 [D4× D8]	D2× D4			[2,2,4] = [2]×[4]	32	[2]+	-	1	1	2	2
D2А2	± 1/2 [D4× D6]	D2× D3			[2,2,3] = [2]×[3]	24	[3]+	-	1	1	3
D2грамм2	± 1/2 [D4× D12]	D2× D6			[2,2,6] = [2]×[6]	48		-	1	1	3	3
D2ЧАС2	± 1/2 [D4× D10]	D2× D5			[2,2,5] = [2]×[5]	40	[5]+	-	1	1	5
2B2	± 1/2 [D8× D8]	D42			[4,2,4] = [4]2	64	[2+,2,2+]	8	2	2	2	2
B2А2	± 1/2 [D8× D6]	D4× D3			[4,2,3] = [4]×[3]	48	[2+,2,3+]	-	2	2	3
B2грамм2	± 1/2 [D8× D12]	D4× D6			[4,2,6] = [4]×[6]	96		-	2	2	3	3
B2ЧАС2	± 1/2 [D8× D10]	D4× D5			[4,2,5] = [4]×[5]	80	[2+,2,5+]	-	2	2	5
2А2	± 1/2 [D6× D6]	D32			[3,2,3] = [3]2	36	[3+,2,3+]	6	3		3
А2грамм2	± 1/2 [D6× D12]	D3× D6			[3,2,6] = [3]×[6]	72		-	3		3	3
2G2	± 1/2 [D12× D12]	D62			[6,2,6] = [6]2	144		12	3	3	3	3
А2ЧАС2	± 1/2 [D6× D10]	D3× D5			[3,2,5] = [3]×[5]	60	[3+,2,5+]	-	3		5
грамм2ЧАС2	± 1/2 [D12× D10]	D6× D5			[6,2,5] = [6]×[5]	120		-	3	3	5
2H2	± 1/2 [D10× D10]	D52			[5,2,5] = [5]2	100	[5+,2,5+]	10	5		5
В общем, p, q = 2,3,4 ...
2I2(2p)	± 1/2 [D4p× D4p]	D2p2			[2p, 2,2p] = [2p]2	16p2	[п+, 2, п+]	2p	п	п	п	п
2I2(п)	± 1/2 [D2p× D2p]	Dп2			[p, 2, p] = [p]2	4p2		2p	п		п
я2(число Пи2(q)	± 1/2 [D4p× D4кв.]	D2p× D2кв.			[2p, 2,2q] = [2p] × [2q]	16пк	[п+, 2, д+]	-	п	п	q	q
я2(число Пи2(q)	± 1/2 [D2p× D2кв.]	Dп× Dq			[p, 2, q] = [p] × [q]	4шт		-	п		q

Порядок симметрии равен количеству ячеек правильного полихорона, умноженному на симметрию его ячеек. У полностью усеченных двойных полихор есть клетки, которые соответствуют основным доменам группы симметрии.

Сети для выпуклые правильные 4-многогранники и полностью усеченные двойники

Симметрия	А4	D4	B4	F4	ЧАС4
4-многогранник	5-элементный	demitesseract	тессеракт	24-элементный	120 ячеек
Клетки	5 {3,3}	16 {3,3}	8 {4,3}	24 {3,4}	120 {5,3}
Симметрия клеток	[3,3], порядок 24		[4,3], порядок 48		[5,3], порядок 120
Диаграмма Кокстера		=
4-многогранник сеть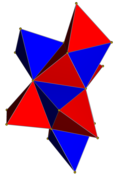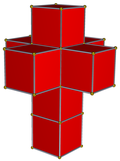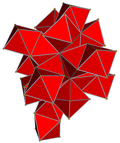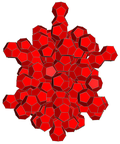
Омнитуркация	всенаправленный. 5-элементный	всенаправленный. demitesseract	всенаправленный. тессеракт	всенаправленный. 24-элементный	всенаправленный. 120 ячеек
Омнитуркация двойной сеть
Диаграмма Кокстера
Клетки	5×24 = 120	(16/2)×24 = 192	8×48 = 384	24×48 = 1152	120×120 = 14400

Киральные подгруппы

В 16 ячеек края проецируются на 3-сфера представляют 6 большие круги симметрии B4. 3 круга встречаются в каждой вершине. Каждый кружок представляет оси 4-й симметрии.

В 24-элементный ребра, проецируемые на 3-сферу, представляют собой 16 больших кругов симметрии F4. В каждой вершине встречаются четыре круга. Каждый кружок представляет оси 3-й симметрии.

В 600 ячеек ребра, проецируемые на 3-сферу, представляют собой 72 больших круга симметрии H4. Шесть кругов пересекаются в каждой вершине. Каждый кружок представляет оси 5-ти кратной симметрии.

Прямые подгруппы рефлексивных 4-мерных точечных групп:

Coxeter обозначение		Конвей Кватернион	Структура	Заказ	Оси вращения
Полихорические группы
	[3,3,3]+	+1/60 [I ×я]	А5	60			103	102
	[[3,3,3]]+	± 1/60 [I ×я]	А5× Z2	120			103	(10+?)2
	[31,1,1]+	± 1/3 [Т × Т]	1/2.2А4	96			163	182
	[4,3,3]+	± 1/6 [O × O]	2А4 = А2≀A4	192	64		163	362
	[3,4,3]+	± 1/2 [O × O]	3.2А4	576	184	163	163	722
	[3+,4,3+]	± [Т × Т]		288		163	163	(72+18)2
	[[3+,4,3+]]	± [O × T]		576			323	(72+18+?)2
	[[3,4,3]]+	± [O × O]		1152	184		323	(72+?)2
	[5,3,3]+	± [I × I]	2. (А5× А5)	7200		725	2003	4502
Многогранные призматические группы
	[3,3,2]+	+1/24[O ×О]	А4× Z2	24		43	43	(6+6)2
	[4,3,2]+	± 1/24 [O × O]	S4× Z2	96		64	83	(3+6+12)2
	[5,3,2]+	± 1/60 [I × I]	А5× Z2	240		125	203	(15+30)2
Дуопризматические группы
	[2,2,2]+	+1/2 [D4× D4]		8		12	12	42
	[3,2,3]+	+1/2 [D6× D6]		18		13	13	92
	[4,2,4]+	+1/2 [D8× D8]		32		14	14	162
(p, q = 2,3,4 ...), НОД (p, q) = 1
	[п, 2, п]+	+1/2 [D2p× D2p]		2p2		1п	1п	(пп)2
	[p, 2, q]+	+1/2 [D2p× D2кв.]		2pq		1п	1q	(pq)2
	[п+, 2, д+]	+ [Cп× Сq]	Zп× Zq	pq		1п	1q

Пентахорическая симметрия

• Пентахорическая группа – А₄, [3,3,3], (), заказ 120, (Du Val # 51 '(I^†/ C₁;IC₁)^†*, Конвей +¹/₆₀[I × I] .2₁), названный в честь 5-элементный (пентахорон), данный кольчатым Диаграмма Кокстера . Его также иногда называют гипертетраэдрическая группа для расширения тетраэдрическая группа [3,3]. В этой группе 10 зеркальных гиперплоскостей. Он изоморфен Абстрактные симметричная группа, S₅.
  • В расширенная пентахорическая группа, Aut(А₄), [[3,3,3]], (На удвоение можно намекнуть свернутой диаграммой, ), заказ 240, (Du Val # 51 (I^†*/ C₂;IC₂)^†*, Конвей ±¹/₆₀[I ×я] .2). Он изоморфен прямому произведению абстрактных групп: S₅× С₂.
    • В киральная расширенная пентахорическая группа это [[3,3,3]]⁺, (), заказ 120, (Du Val # 32 (I^†/ C₂;IC₂)^†, Конвей ±¹/₆₀[Ixя]). Эта группа представляет собой конструкцию омниснуб 5-элементный, , хотя его нельзя сделать единообразным. Он изоморфен прямому произведению абстрактных групп: A₅× С₂.
  • В хиральная пентахорическая группа это [3,3,3]⁺, (), заказ 60, (Du Val # 32 '(I^†/ C₁;IC₁)^†, Конвей +¹/₆₀[I ×я]). Он изоморфен Абстрактные переменная группа, А₅.
    • В расширенная киральная пентахорическая группа это [[3,3,3]⁺], заказ 120, (Du Val # 51 "(I^†/ C₁;IC₁)_–^†*, Конвей +¹/₆₀[IxI] .2₃). Кокстер относит эту группу к абстрактной группе (4,6 | 2,3).^[13] Он также изоморфен Абстрактные симметричная группа, S₅.

Гексадекахорическая симметрия

• Гексадекахорическая группа – B₄, [4,3,3], (), заказ 384, (Du Val # 47 (O / V; O / V)^*, Конвей ±¹/₆[O × O] .2), названный в честь 16 ячеек (гексадекахорон), . В этой группе 16 зеркальных гиперплоскостей, которые можно идентифицировать в 2 ортогональных наборах: 12 из [3^1,1,1] подгруппа и 4 из [2,2,2] подгруппы. Его также называют гипероктаэдрическая группа для расширения 3D октаэдрическая группа [4,3], а тессератическая группа для тессеракт, .
  • В хиральная гексадекахорическая группа это [4,3,3]⁺, (), заказ 192, (Du Val # 27 (O / V; O / V), Conway ±¹/₆[O × O]). Эта группа представляет собой конструкцию омниснуб тессеракт, , хотя его нельзя сделать единообразным.
  • В ионная уменьшенная гексадекахорная группа равно [4, (3,3)⁺], (), заказ 192, (Du Val # 41 (T / V; T / V)^*, Конвей ±¹/₃[Т × Т] .2). Эта группа приводит к курносый 24-элементный со строительством .
  • В половина шестнадцатеричной группы это [1⁺,4,3,3], ( = ), заказ 192, такой же, как у #demitesseractic симметрия: [3^1,1,1]. Эта группа выражается в тессеракт чередовались строительство 16 ячеек, = .
    • Группа [1⁺,4,(3,3)⁺], ( = ), порядок 96, и такой же, как у хиральная демитессератическая группа [3^1,1,1]⁺ а также коммутаторная подгруппа из [4,3,3].
  • Отражательная подгруппа с высоким индексом - это призматическая октаэдрическая симметрия, [4,3,2] (), порядок 96, индекс подгруппы 4, (Du Val # 44 (O / C₂; O / C₂)^*, Конвей ±¹/₂₄[O × O] .2). В усеченная кубическая призма имеет эту симметрию с диаграммой Кокстера и кубическая призма является конструкцией нижней симметрии тессеракт, так как .
    • Его киральная подгруппа [4,3,2]⁺, (), заказ 48, (Du Val # 26 (O / C₂; O / C₂), Конвей ±¹/₂₄[O × O]). Примером может служить курносая кубическая антипризма, , хотя его нельзя сделать единообразным.
    • Ионные подгруппы:
      • [(3,4)⁺,2], (), заказ 48, (Du Val # 44b '(O / C₁; O / C₁)₋^*, Конвей +¹/₂₄[O × O] .2₁). В курносая кубическая призма имеет эту симметрию с диаграммой Кокстера .
        • [(3,4)⁺,2⁺], (), заказ 24, (Du Val # 44 '(T / C₂; Т / К₂)₋^*, Конвей +¹/₁₂[Т × Т] .2₁).
      • [4,3⁺,2], (), заказ 48, (Du Val # 39 (T / C₂; Т / К₂)_c^*, Конвей ±¹/₁₂[Т × Т] .2).
        • [4,3⁺,2,1⁺] = [4,3⁺,1] = [4,3⁺], ( = ), заказ 24, (Du Val # 44 "(T / C₂; Т / К₂)^*, Конвей +¹/₁₂[Т × Т] .2₃). Это 3D пиритоэдрическая группа, [4,3⁺].
        • [3⁺,4,2⁺], (), заказ 24, (Du Val # 21 (T / C₂; Т / К₂), Конвей ±¹/₁₂[Т × Т]).
      • [3,4,2⁺], (), заказ 48, (Du Val # 39 '(T / C₂; Т / К₂)₋^*, Конвей ±¹/₁₂[T ×Т].2).
      • [4,(3,2)⁺], (), заказ 48, (Du Val # 40b '(O / C₁; O / C₁)₋^*, Конвей +¹/₂₄[O ×О].2₁).
    • Полуподгруппа [4,3,2,1⁺] = [4,3,1] = [4,3], ( = ), заказ 48 (Du Val # 44b "(O / C₁; O / C₁)_c^*, Конвей +¹/₂₄[O × O] .2₃). Это называется октаэдрическая пирамидальная группа и это 3D октаэдрическая симметрия, [4,3]. А кубическая пирамида может иметь эту симметрию, с Символ Шлефли: ( ) ∨ {4,3}.
      

      [4,3], , октаэдрическая пирамидальная группа изоморфен 3d октаэдрическая симметрия
      • Киральная полуподгруппа [(4,3)⁺,2,1⁺] = [4,3,1]⁺ = [4,3]⁺, ( = ), заказ 24 (Du Val # 26b '(O / C₁; O / C₁), Конвей +¹/₂₄[O × O]). Это 3D хиральная октаэдрическая группа, [4,3]⁺. А курносая кубическая пирамида может иметь эту симметрию с символом Шлефли: () ∨ sr {4,3}.
  • Другая подгруппа отражателей с высоким показателем - это призматическая тетраэдрическая симметрия, [3,3,2], (), порядок 48, индекс подгруппы 8, (Du Val # 40b "(O / C₁; O / C₁)^*, Конвей +¹/₂₄[O ×О].2₃).
    • Киральная подгруппа [3,3,2]⁺, (), заказ 24, (Du Val # 26b "(O / C₁; O / C₁), Конвей +¹/₂₄[O ×О]). Примером может служить курносая тетраэдрическая антипризма, , хотя его нельзя сделать единообразным.
    • Ионная подгруппа [(3,3)⁺,2], (), заказ 24, (Du Val # 39b '(T / C₁; Т / К₁)_c^*, Конвей +¹/₁₂[T ×Т].2₃). Примером может служить плоскостная тетраэдрическая призма, .
    • Полуподгруппа [3,3,2,1⁺] = [3,3,1] = [3,3], ( = ), заказ 24, (Du Val # 39b "(T / C₁; Т / К₁)₋^*, Конвей +¹/₁₂[T ×Т].2₁). Это называется тетраэдрическая пирамидальная группа и это 3D тетраэдрическая группа, [3,3]. Обычный четырехгранная пирамида может иметь эту симметрию с символом Шлефли: () ∨ {3,3}.
      

      [3,3], , тетраэдрическая пирамидальная группа изоморфен 3d тетраэдрическая симметрия
      • Киральная полуподгруппа [(3,3)⁺,2,1⁺] = [3,3]⁺( = ), заказ 12, (Du Val # 21b '(T / C₁; Т / К₁), Конвей +¹/₁₂[Т × Т]). Это 3D хиральная тетраэдрическая группа, [3,3]⁺. А плоскостная четырехгранная пирамида может иметь эту симметрию с символом Шлефли: () ∨ sr {3,3}.
  • Другая радиальная отражательная подгруппа с высоким показателем преломления - это [4, (3,3)^*], индекс 24, удаляет зеркала с двугранными углами порядка 3, создавая [2,2,2] (), порядок 16. Остальные - [4,2,4] (), [4,2,2] (), с индексами подгруппы 6 и 12, порядков 64 и 32. Эти группы являются нижними симметриями группы тессеракт: (), (), и (). Эти группы # дуопризматическая симметрия.

Икоситетрахорическая симметрия

• Икоситетрахорическая группа – F₄, [3,4,3], (), заказ 1152, (Du Val # 45 (O / T; O / T)^*, Конвей [O × O] .2₃), названный в честь 24-элементный (икоситетрахорон), . В этой симметрии 24 зеркальных плоскости, которые можно разложить на два ортогональных набора по 12 зеркал в демитессератическая симметрия [3^1,1,1] подгруппы, как [3^*, 4,3] и [3,4,3^*], как подгруппы индекса 6.
  • В расширенная икозитетрахорическая группа, Aut(F₄), [[3,4,3]], () имеет заказ 2304, (Du Val # 48 (O / O; O / O)^*, Конвей ± [O × O] .2).
    • В хиральная расширенная икоситетрахорическая группа, [[3,4,3]]⁺, () имеет порядок 1152, (Du Val # 25 (O / O; O / O), Conway ± [OxO]). Эта группа представляет собой конструкцию omnisnub 24 ячейки, , хотя его нельзя сделать единообразным.
  • В ионные уменьшенные икозитетрахорические группы, [3⁺, 4,3] и [3,4,3⁺], ( или же ), имейте заказ 576, (Du Val # 43 (T / T; T / T)^*, Конвей ± [T × T]. 2). Эта группа приводит к курносый 24-элементный со строительством или же .
    • В двойно уменьшенная икозитетрахорическая группа, [3⁺,4,3⁺] (двойное уменьшение можно показать разрывом в 4-ветви диаграммы: ), заказ 288, (Du Val # 20 (T / T; T / T), Conway ± [T × T]) является коммутаторная подгруппа из [3,4,3].
      • Его можно расширить как [[3⁺,4,3⁺]], () приказ 576, (Du Val # 23 (T / T; O / O), Conway ± [OxT]).
  • В хиральная икозитетрахорическая группа это [3,4,3]⁺, (), заказ 576, (Du Val # 28 (O / T; O / T), Conway ±¹/₂[O × O]).
    • В расширенная хиральная икозитетрахорическая группа, [[3,4,3]⁺] имеет заказ 1152, (Du Val № 46 (O / T; O / T)₋^*, Конвей ±¹/₂[OxO].2). Кокстер относит эту группу к абстрактной группе (4,8 | 2,3).^[13]

Демитессератическая симметрия

• Демитессератическая группа – D₄, [3^1,1,1], [3,3^1,1] или [3,3,4,1⁺], ( = ), заказ 192, (Du Val # 42 (T / V; T / V)₋^*, Конвей ±¹/₃[T ×Т] .2), названный в честь (demitesseract) 4-полукуб строительство 16-ти клеточной, или же . В этой группе симметрии 12 зеркал.
  • Есть два типа расширенных симметрий путем добавления зеркал: <[3,3^1,1]> который становится [4,3,3] путем деления пополам фундаментальной области зеркалом, с 3 возможными ориентациями; и полная расширенная группа [3 [3^1,1,1]] становится [3,4,3].
  • В хиральная демитессератическая группа равно [3^1,1,1]⁺ или [1⁺,4,(3,3)⁺], ( = ), заказ 96, (Du Val # 22 (T / V; T / V), Conway ±¹/₃[Т × Т]). Эта группа приводит к курносый 24-элементный со строительством = .

Гексакозихорическая симметрия

[5,3,3]+ 72 порядка 5 оборотов	[5,3,3]+ 200 оборотов порядка-3
[5,3,3]+ 450 оборотов порядка-2	[5,3,3]+ все вращения
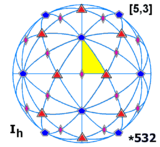[5,3], , икосаэдрическая пирамидальная группа изоморфен 3d икосаэдрическая симметрия

• Гексакозихорическая группа – ЧАС₄, [5,3,3], (), заказ 14400, (Du Val # 50 (I / I; I / I)^*, Конвей ± [I × I] .2), названный в честь 600 ячеек (гексакосихорон), . Его также иногда называют группа гиперикосаэдра для расширения 3D группа икосаэдров [5,3], и гекатоникосахорическая группа или же додекаконтахорическая группа от 120 ячеек, .
  • В хиральная гексакосихорическая группа это [5,3,3]⁺, (), заказ 7200, (Du Val # 30 (I / I; I / I), Conway ± [I × I]). Эта группа представляет собой конструкцию курносый 120-элементный, , хотя его нельзя сделать единообразным.
  • Отражательная подгруппа с высоким индексом - это призматическая икосаэдрическая симметрия, [5,3,2], (), порядок 240, индекс подгруппы 60, (Du Val # 49 (I / C₂;IC₂)^*, Конвей ±¹/₆₀[IxI] .2).
    • Его киральная подгруппа [5,3,2]⁺, (), заказ 120, (Du Val # 31 (I / C₂;IC₂), Конвей ±¹/₆₀[IxI]). Эта группа представляет собой конструкцию курносая додекаэдрическая антипризма, , хотя его нельзя сделать единообразным.
    • Ионная подгруппа [(5,3)⁺,2], (), заказ 120, (Du Val # 49 '(I / C₁;IC₁)^*, Конвей +¹/₆₀[IxI] .2₁). Эта группа представляет собой конструкцию курносая додекаэдрическая призма, .
    • Полуподгруппа [5,3,2,1⁺] = [5,3,1] = [5,3], ( = ), заказ 120, (Du Val # 49 "(I / C₁;IC₁)₋^*, Конвей +¹/₆₀[IxI] .2₃). Это называется икосаэдрическая пирамидальная группа и это 3D группа икосаэдров, [5,3]. Обычный додекаэдрическая пирамида может иметь эту симметрию, с Символ Шлефли: ( ) ∨ {5,3}.
      • Киральная полуподгруппа [(5,3)⁺,2,1⁺] = [5,3,1]⁺ = [5,3]⁺, ( = ), заказ 60, (Du Val # 31 '(I / C₁;IC₁), Конвей +¹/₆₀[IxI]). Это 3D хиральная группа икосаэдра, [5,3]⁺. А курносая додекаэдрическая пирамида может иметь эту симметрию, с Символ Шлефли: () ∨ sr {5,3}.

Дуопризматическая симметрия

• Дуопризматические группы - [p, 2, q], (), порядок 4pqсуществуют для всех 2 ≤п,q <∞. В этой симметрии имеется p + q зеркал, которые тривиально разлагаются на два ортогональных набора из p и q зеркал. двугранная симметрия: [p] и [q].
  • Киральная подгруппа [p, 2, p]⁺,(), порядок 2pq. Его можно удвоить как [[2p, 2,2p]⁺].
  • Если p и q равны, [p, 2, p], () симметрию можно удвоить как [[p, 2, p]], ().
    • Удвоение: [[p⁺, 2, п⁺]], (), [[2p, 2⁺, 2p]], [[2p⁺,2⁺, 2п⁺]].
  • [p, 2, ∞], (), он представляет собой группы линий в 3-м пространстве,
  • [∞,2,∞], () он представляет собой симметрию евклидовой плоскости с двумя наборами параллельных зеркал и прямоугольной областью (орбифолд *2222).
  • Подгруппы включают: [p⁺, 2, q], (), [p, 2, q⁺], (), [п⁺, 2, д⁺], ().
  • И для четных значений: [2p, 2⁺, 2q], (), [2p, 2⁺, 2q⁺], (), [(p, 2)⁺, 2q], (), [2p, (2, q)⁺], (), [(p, 2)⁺, 2q⁺], (), [2p⁺, (2, q)⁺], (), [2p⁺,2⁺, 2q⁺], () и коммутаторная подгруппа, индекс 16, [2p⁺,2⁺, 2q⁺]⁺, ().
• Дигональная дуопризматическая группа – [2,2,2], (), заказ 16.
  • Киральная подгруппа [2,2,2]⁺, (), заказ 8.
  • Расширенный [[2,2,2]], (), заказ 32. 4-4 дуопризма обладает этой расширенной симметрией, .
    • Киральная расширенная группа [[2,2,2]]⁺, заказ 16.
    • Расширенная киральная подгруппа [[2,2,2]⁺], заказ 16, с вращательное отражение генераторы. Он изоморфен абстрактной группе (4,4 | 2,2).
  • Другой расширенный [(3,3) [2,2,2]] = [4,3,3], порядок 384, # Шестнадцатеричная кахорическая симметрия. В тессеракт обладает этой симметрией, поскольку или же .
  • Ионно уменьшенные подгруппы [2⁺, 2,2], порядок 8.
    • Двойная уменьшенная подгруппа [2⁺,2,2⁺], порядок 4.
      • Расширен как [[2⁺,2,2⁺]], заказ 8.
    • Подгруппы вращательного отражения [2⁺,2⁺,2], [2,2⁺,2⁺], [2⁺,(2,2)⁺], [(2,2)⁺,2⁺] порядок 4.
    • Тройная уменьшенная подгруппа [2⁺,2⁺,2⁺], (), порядок 2. Это 2-кратный двойное вращение и 4D центральная инверсия.
  • Полуподгруппа [1⁺, 2,2,2] = [1,2,2], порядок 8.
• Треугольная дуопризматическая группа – [3,2,3], , заказ 36.
  • Киральная подгруппа [3,2,3]⁺, заказ 18.
  • Расширенный [[3,2,3]], порядок 72. 3-3 дуопризма обладает этой расширенной симметрией, .
    • Киральная расширенная группа [[3,2,3]]⁺, заказ 36.
    • Расширенная киральная подгруппа [[3,2,3]⁺], заказ 36, с вращательное отражение генераторы. Он изоморфен абстрактной группе (4,4 | 2,3).
  • Остальные расширенные [[3], 2,3], [3,2, [3]], порядок 72, изоморфны [6,2,3] и [3,2,6].
  • И [[3], 2, [3]], порядок 144, и изоморфен [6,2,6].
  • И [[[3], 2, [3]]], порядок 288, изоморфен [[6,2,6]]. В 6–6 дуопризма обладает этой симметрией, поскольку или же .
  • Ионно уменьшенные подгруппы [3⁺,2,3], [3,2,3⁺], заказ 18.
    • Двойная уменьшенная подгруппа [3⁺,2,3⁺], заказ 9.
      • Расширен как [[3⁺,2,3⁺]], заказ 18.
  • Подгруппа с высоким индексом [3,2], порядок 12, индекс 3, изоморфна группе двугранная симметрия в трех измерениях группа, [3,2], D_3ч.
    • [3,2]⁺, заказ 6
• Квадратная дуопризматическая группа – [4,2,4], , заказ 64.
  • Киральная подгруппа [4,2,4]⁺, заказ 32.
  • Расширенный [[4,2,4]], порядок 128. 4–4 дуопризма обладает этой расширенной симметрией, .
    • Киральная расширенная группа [[4,2,4]]⁺, заказ 64.
    • Расширенная киральная подгруппа [[4,2,4]⁺], заказ 64, с вращательное отражение генераторы. Он изоморфен абстрактной группе (4,4 | 2,4).
  • Остальные расширены [[4], 2,4], [4,2, [4]], порядок 128 и изоморфны [8,2,4] и [4,2,8]. В 4–8 дуопризма обладает этой симметрией, поскольку или же .
  • И [[4], 2, [4]], порядок 256, и изоморфен [8,2,8].
  • И [[[4], 2, [4]]], порядок 512, изоморфен [[8,2,8]]. В 8–8 дуопризма обладает этой симметрией, поскольку или же .
  • Ионно уменьшенные подгруппы [4⁺,2,4], [4,2,4⁺], заказ 32.
    • Двойная уменьшенная подгруппа [4⁺,2,4⁺], заказ 16.
      • Расширен как [[4⁺,2,4⁺]], заказ 32.
    • Подгруппами вращательного отражения являются [4⁺,2⁺,4], [4,2⁺,4⁺], [4⁺,(2,4)⁺], [(4,2)⁺,4⁺], (, , , ) заказ 16.
    • Тройная уменьшенная подгруппа [4⁺,2⁺,4⁺], (), заказ 8.
  • Полуподгруппы составляют [1⁺,4,2,4]=[2,2,4], (), [4,2,4,1⁺]=[4,2,2], (), заказ 32.
    • [1⁺,4,2,4]⁺=[2,2,4]⁺, (), [4,2,4,1⁺]⁺=[4,2,2]⁺, (), заказ 16.
  • Снова половина подгруппы [1⁺,4,2,4,1⁺]=[2,2,2], (), заказ 16.
    • [1⁺,4,2,4,1⁺]⁺ = [1⁺,4,2⁺,4,1⁺] = [2,2,2]⁺, () заказ 8

Резюме

Это сводка 4-х мерного точечные группы в Обозначение Кокстера. 227 из них являются кристаллографическими точечными группами (для определенных значений p и q).^[14] (nc) дан для некристаллографических групп. Порядки некоторых кристаллографических групп индексируются (order.index) по их абстрактной групповой структуре.^[15]

Конечные группы
[ ]: Символ Заказ [1]+ 1.1 [1] = [ ] 2.1 [2]: Символ Заказ [1+,2]+ 1.1 [2]+ 2.1 [2] 4.1 [2,2]: Символ Заказ [2+,2+]+ = [(2+,2+,2+)] 1.1 [2+,2+] 2.1 [2,2]+ 4.1 [2+,2] 4.1 [2,2] 8.1 [2,2,2]: Символ Заказ [(2+,2+,2+,2+)] = [2+,2+,2+]+ 1.1 [2+,2+,2+] 2.1 [2+,2,2+] 4.1 [(2,2)+,2+] 4 [[2+,2+,2+]] 4 [2,2,2]+ 8 [2+,2,2] 8.1 [(2,2)+,2] 8 [[2+,2,2+]] 8.1 [2,2,2] 16.1 [[2,2,2]]+ 16 [[2,2+,2]] 16 [[2,2,2]] 32	[п]: Символ Заказ [п]+ п [п] 2p [p, 2]: Символ Заказ [п,2]+ 2п [п,2] 4п [2п, 2+]: Символ Заказ [2п,2+] 4п [2п+,2+] 2п [п,2,2]: Символ Заказ [п+,2,2+] 2п [(п,2)+,2+] 2п [п,2,2]+ 4п [п,2,2+] 4п [п+,2,2] 4п [(p, 2)+,2] 4п [п, 2,2] 8п [2п,2+,2]: Символ Заказ [2п+,2+,2+]+ п [2п+,2+,2+] 2п [2п+,2+,2] 4п [2п+,(2,2)+] 4п [2п,(2,2)+] 8п [2п,2+,2] 8п	[п,2,q]: Символ Заказ [п+,2,q+] pq [п,2,q]+ 2pq [п+,2,q] 2pq [п,2,q] 4pq [(п,2)+,2q]: Символ Заказ [(п,2)+,2q+] 2pq [(п,2)+,2q] 4pq [2п,2,2q]: Символ Заказ [2п+,2+,2q+]+= [(2п+,2+,2q+,2+)] pq [2п+,2+,2q+] 2pq [2п,2+,2q+] 4pq [((2п,2)+,(2q,2)+)] 4pq [2п,2+,2q] 8pq [[п,2,п]]: Символ Заказ [[п+,2,п+]] 2п2 [[п,2,п]]+ 4п2 [[п,2,п]+] 4п2 [[п,2,п]] 8п2 [[2п,2,2п]]: Символ Заказ [[(2п+,2+,2п+,2+)]] 2п2 [[2п+,2+,2п+]] 4п2 [[((2п,2)+,(2п,2)+)]] 8п2 [[2п,2+,2п]] 16п2	[3,3,2]: Символ Заказ [(3,3)Δ,2,1+] ≅ [2,2]+ 4 [(3,3)Δ,2] ≅ [2,(2,2)+] 8 [(3,3)⅄,2,1+] ≅ [4,2+] 8 [(3,3)+,2,1+] = [3,3]+ 12.5 [(3,3)⅄,2] ≅ [2,4,2+] 16 [3,3,2,1+] = [3,3] 24 [(3,3)+,2] 24.10 [3,3,2]+ 24.10 [3,3,2] 48.36 [4,3,2]: Символ Заказ [1+,4,3+,2,1+] = [3,3]+ 12 [3+,4,2+] 24 [(3,4)+,2+] 24 [1+,4,3+,2] = [(3,3)+,2] 24.10 [3+,4,2,1+] = [3+,4] 24.10 [(4,3)+,2,1+] = [4,3]+ 24.15 [1+,4,3,2,1+] = [3,3] 24 [1+,4,(3,2)+] = [3,3,2]+ 24 [3,4,2+] 48 [4,3+,2] 48.22 [4,(3,2)+] 48 [(4,3)+,2] 48.36 [1+,4,3,2] = [3,3,2] 48.36 [4,3,2,1+] = [4,3] 48.36 [4,3,2]+ 48.36 [4,3,2] 96.5 [5,3,2]: Символ Заказ [(5,3)+,2,1+] = [5,3]+ 60.13 [5,3,2,1+] = [5,3] 120.2 [(5,3)+,2] 120.2 [5,3,2]+ 120.2 [5,3,2] 240 (нк)	[31,1,1]: Символ Заказ [31,1,1]Δ ≅[[4,2+,4]]+ 32 [31,1,1]⅄ 64 [31,1,1]+ 96.1 [31,1,1] 192.2 <[3,31,1]> = [4,3,3] 384.1 [3[31,1,1]] = [3,4,3] 1152.1 [3,3,3]: Символ Заказ [3,3,3]+ 60.13 [3,3,3] 120.1 [[3,3,3]]+ 120.2 [[3,3,3]+] 120.1 [[3,3,3]] 240.1 [4,3,3]: Символ Заказ [1+,4,(3,3)Δ] = [31,1,1]Δ ≅[[4,2+,4]]+ 32 [4,(3,3)Δ] = [2+,4[2,2,2]+] ≅[[4,2+,4]] 64 [1+,4,(3,3)⅄] = [31,1,1]⅄ 64 [1+,4,(3,3)+] = [31,1,1]+ 96.1 [4,(3,3)⅄] ≅ [[4,2,4]] 128 [1+,4,3,3] = [31,1,1] 192.2 [4,(3,3)+] 192.1 [4,3,3]+ 192.3 [4,3,3] 384.1 [3,4,3]: Символ Заказ [3+,4,3+] 288.1 [3,4,3⅄] = [4,3,3] 384.1 [3,4,3]+ 576.2 [3+,4,3] 576.1 [[3+,4,3+]] 576 (нк) [3,4,3] 1152.1 [[3,4,3]]+ 1152 (нк) [[3,4,3]+] 1152 (нк) [[3,4,3]] 2304 (нк) [5,3,3]: Символ Заказ [5,3,3]+ 7200 (нк) [5,3,3] 14400 (нк)

Смотрите также

• Группа точек
• Группы точек в двух измерениях
• Группы точек в трех измерениях

Рекомендации

• H.S.M. Кокстер, Правильные многогранники, 3-е издание, Довер, Нью-Йорк, 1973
• Калейдоскопы: Избранные произведения Х.С.М. Coxeter, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6
  • (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
  • (Документ 23) Х.С.М. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) 559–591]
  • (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3–45]
• H.S.M. Кокстер и У. О. Дж. Мозер. Генераторы и отношения для дискретных групп 4-е изд., Springer-Verlag. Нью-Йорк. 1980 с.92, с122.
• Джон .H. Конвей и M.J.T. Парень: Четырехмерные архимедовы многогранники, Труды коллоквиума по выпуклости в Копенгагене, стр. 38 и 39, 1965 г.
• N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. Диссертация, Университет Торонто, 1966 г.
• N.W. Джонсон: Геометрии и преобразования, (2018) ISBN 978-1-107-10340-5 Глава 11: Конечные группы симметрии, 11.5 Сферические группы Кокстера, стр.249
• Джон Х. Конвей и Дерек А. Смит, О кватернионах и октонионах, 2003, ISBN 978-1-56881-134-5
• Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Страсс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26)

внешняя ссылка

• Вайсштейн, Эрик В. «Равномерный полихорон». MathWorld.
• Клитцинг, Ричард. "4D однородные многогранники".