WikiDer > Полиграмма (геометрия)
В геометрия, обобщенный многоугольник можно назвать полиграмма, и назван конкретно по количеству сторон. Например, обычный пентаграмма, {5/2}, имеет 5 сторон, а обычный гексаграмма, {6/2} или 2 {3}, имеет 6 сторон, разделенных на два треугольника.
А регулярная полиграмма {п/q} может быть либо в наборе правильные многоугольники (за gcd(п,q) = 1, q > 1) или в наборе правильные многоугольники (если gcd (п,q) > 1).[1]
Этимология
Имена полиграмм сочетают в себе цифровой префикс, Такие как пента-, с Греческий суффикс -грамма (в этом случае генерируя слово пентаграмма). Префикс обычно греческий кардинал, но существуют синонимы, использующие другие префиксы. В -грамма суффикс происходит от γραμμῆς (граммы) означает строку.[2]
Обобщенные правильные многоугольники
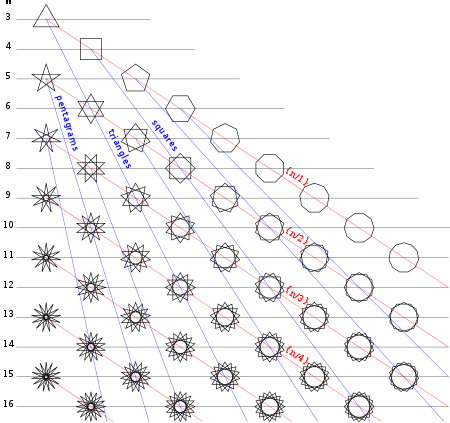
Правильная полиграмма, как генерал правильный многоугольник, обозначается его Символ Шлефли {п/q}, куда п и q находятся относительно простой (у них нет общих факторов) и q ≥ 2. Для целые числа п и q, его можно считать построенным путем соединения каждого qй пункт из п точки, расположенные равномерно по кругу.[3][4]
 {5/2} |  {7/2} |  {7/3} |  {8/3} |  {9/2} |  {9/4} |  {10/3}... |
Правильные составные многоугольники
В других случаях, когда п и м есть общий фактор, полиграмма интерпретируется как нижний многоугольник, {п/k, м/k}, с k = gcd (п,м), а повернутые копии объединяются в составной многоугольник. Эти цифры называются правильные составные многоугольники.
| Треугольники ... | Квадраты ... | Пентагоны ... | Пентаграммы ... | ||||
|---|---|---|---|---|---|---|---|
 {6/2}=2{3} | 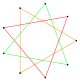 {9/3}=3{3} |  {12/4}=4{3} |  {8/2}=2{4} |  {12/3}=3{4} |  {10/2}=2{5} |  {10/4}=2{5/2} |  {15/6}=3{5/2} |
Смотрите также
Рекомендации
- ^ Вайсштейн, Эрик В. «Полиграмм». MathWorld.
- ^ γραμμή, Генри Джордж Лидделл, Роберт Скотт, Греко-английский лексикон, на Персее
- ^ Кокстер, Гарольд Скотт Макдональд (1973). Правильные многогранники. Courier Dover Publications. п.93. ISBN 978-0-486-61480-9.
- ^ Вайсштейн, Эрик В. «Полиграмм». MathWorld.
- Cromwell, P .; Многогранники, CUP, Hbk. 1997, ISBN 0-521-66432-2. Pbk. (1999), ISBN 0-521-66405-5. п. 175
- Грюнбаум, Б. и G.C. Шепард; Плитки и узоры, Нью-Йорк: W. H. Freeman & Co., (1987), ISBN 0-7167-1193-1.
- Grünbaum, B .; Многогранники с полыми гранями, Протокол конференции НАТО-АСИ по многогранникам ... и т. Д. (Торонто, 1993 г.), под ред. Т. Бистрички и др., Kluwer Academic (1994), стр. 43–70.
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26. с. 404: Правильные звездные многогранники размерности 2)
- Роберт Лахлан, Элементарный трактат о современной чистой геометрии. Лондон: Macmillan, 1893, стр. 83 полиграммы.
- Бранко Грюнбаум, Метаморфозы полигонов, опубликовано в Светлая сторона математики: материалы конференции Мемориала Эжена Стренса по развлекательной математике и ее истории, (1994)