WikiDer > Цепь Штейнера
В геометрия, а Цепь Штейнера это набор п окружности, каждый из которых касается двух заданных непересекающихся окружностей (синий и красный на рисунке 1), где п конечна, и каждая окружность в цепочке касается предыдущей и следующей окружностей в цепочке. В обычном закрыто Цепи Штейнера первая и последняя (пth) окружности также касаются друг друга; напротив, в открыто Цепи Штейнера, они не должны быть. Данные круги α и β не пересекаются, но в остальном не ограничены; меньший круг может полностью лежать внутри или вне большего круга. В этих случаях центры окружностей цепей Штейнера лежат на эллипс или гипербола, соответственно.
Цепи Штайнера названы в честь Якоб Штайнер, который определил их в XIX веке и открыл многие из их свойств. Фундаментальный результат Штайнера пористость, в котором говорится:
- Если хотя бы одна замкнутая цепочка Штейнера п круги существует для двух заданных кругов α и β, то существует бесконечное число замкнутых цепочек Штейнера п круги; и любой окружности, касающейся α и β таким же образом входит в такую цепочку.
«Касательная таким же образом» означает, что произвольная окружность касается внутренней или внешней стороны так же, как окружность исходной цепи Штейнера. Поризм - это разновидность теорем, касающихся количества решений и условий на них. Поризмы часто описывают геометрическую фигуру, которая не может существовать, если не выполняется условие, но в противном случае может существовать в бесконечном количестве; другой пример Пористость Понселе.
Методика инверсия круга помогает при лечении цепей Штейнера. Поскольку она сохраняет касания, углы и окружности, инверсия преобразует одну цепочку Штейнера в другую из того же числа окружностей. Один конкретный выбор инверсии преобразует данные круги α и β в концентрические круги; в этом случае все круги цепочки Штейнера имеют одинаковый размер и могут «катиться» в кольцо между кругами, похожими на шарикоподшипники. Эта стандартная конфигурация позволяет вывести несколько свойств цепей Штейнера, например, ее точки касания всегда лежат на окружности. Существует несколько обобщений цепей Штейнера, в первую очередь Гекслет Содди и Цепочки паппуса.[1]
Определения и виды касания
- Цепи Штейнера с различными внутренними / внешними касаниями
Два заданных круга α и β не может пересекаться; следовательно, меньший заданный круг должен лежать внутри или снаружи большего. Круги обычно показаны как кольцо, т.е. с меньшим заданным кругом внутри большего. В этой конфигурации окружности цепи Штейнера касаются снаружи внутренней окружности и касаются внутренней окружности внешней окружности. Однако меньший круг также может полностью лежать вне большего (Рисунок 2). Черные кружки на рис. 2 удовлетворяют условиям замкнутой цепи Штейнера: все они касаются двух данных окружностей, и каждая касается своих соседей по цепи. В этой конфигурации окружности цепи Штейнера имеют одинаковый тип касания к обеим данным окружностям, либо внешне, либо внутренне касаясь обоих. Если две заданные окружности касаются в одной точке, цепочка Штейнера становится бесконечной. Цепочка паппуса, который часто обсуждается в контексте арбелос (сапожный нож), геометрическая фигура из трех кругов. Нет общего названия для последовательности окружностей, касающихся двух данных окружностей, пересекающихся в двух точках.
Закрытый, открытый и многоцикловый
- Замкнутые, открытые и многоциклические цепи Штейнера
Два заданных круга α и β прикоснуться к п круги цепи Штейнера, но каждый круг Ck цепи Штейнера касается только четырех окружностей: α, β, и его два соседа, Ck−1 и Ck+1. По умолчанию предполагается, что цепи Штейнера закрыто, т.е. первая и последняя окружности касаются друг друга. Напротив, открыто Цепь Штейнера - это цепь, в которой первый и последний круги, C1 и Cп, не касаются друг друга; эти круги касаются только три круги. Мультициклические цепи Штейнера оборачиваются вокруг внутреннего круга более одного раза, прежде чем замкнуться, то есть до того, как они будут касаться начального круга.
Замкнутые цепи Штейнера - это системы окружностей, полученные как теорема об упаковке кругов представление бипирамида.
Кольцевой корпус и критерий выполнимости
- Кольцевые цепи Штейнера
Простейший тип цепочки Штейнера - это замкнутая цепочка п круги равного размера, окружающие вписанный круг радиуса р; сама цепочка кругов окружена описанной окружностью радиуса р. Вписанные и описанные данные окружности концентрические, а окружности цепочки Штейнера лежат в кольцо между ними. По симметрии угол 2θ между центрами окружностей цепи Штейнера - 360 ° /п. Поскольку окружности цепи Штейнера касаются друг друга, расстояние между их центрами равно сумме их радиусов, в данном случае удвоенного радиуса ρ. Биссектриса (зеленая на рисунке) образует два прямоугольных треугольника с центральным углом θ = 180°/п. В синус этого угла можно записать как длину его противоположного сегмента, деленную на гипотенузу прямоугольного треугольника
С θ известно из п, это дает уравнение для неизвестного радиуса ρ кругов цепи Штейнера
Точки касания окружности цепи Штейнера с внутренней и внешней данной окружностями лежат на прямой, проходящей через их общий центр; следовательно, внешний радиус р = р + 2ρ.
Эти уравнения служат критерием выполнимости цепи Штейнера для двух данных концентрических окружностей. Замкнутая цепочка Штейнера п кругов требует, чтобы соотношение радиусов р/р данных кругов равны в точности
Как показано ниже, этот критерий отношения радиусов для концентрических заданных кругов может быть расширен на все типы данных кругов с помощью обратное расстояние δ из двух данных кружков. Для концентрических окружностей это расстояние определяется как логарифм отношения их радиусов.
Используя решение для концентрических окружностей, общий критерий цепочки Штейнера п круги можно написать
Если полициклическая кольцевая цепь Штейнера имеет п всего кругов и витков вокруг м раз до закрытия угол между окружностями цепи Штейнера равен
В остальном критерий осуществимости не изменился.
Свойства при инверсии
- Инверсивные свойства цепей Штейнера
Инверсия круга преобразует одну цепочку Штейнера в другую с таким же количеством кругов.
В преобразованной цепи все точки касания между соседними окружностями цепи Штейнера лежат на окружности, а именно на концентрической окружности посередине между двумя фиксированными концентрическими окружностями. Поскольку касания и окружности сохраняются при инверсии, это свойство всех касаний, лежащих на окружности, верно и в исходной цепи. Это свойство также используется совместно с Цепочка паппуса окружностей, которые можно рассматривать как частный предельный случай цепи Штейнера.
В преобразованной цепочке касательные от О к цепочке Штейнера окружности разделены равными углами. В исходной цепочке это соответствует равным углам между касательными окружностями, которые проходят через центр инверсии, используемым для преобразования исходных окружностей в концентрическую пару.
В преобразованной цепочке п линии, соединяющие пары точек касания окружностей Штейнера с концентрическими окружностями, проходят через О, общий центр. Точно так же п прямые, касательные к каждой паре соседних окружностей в цепочке Штейнера, также проходят через О. Поскольку прямые, проходящие через центр инверсии, инвариантны относительно инверсии, а касание и совпадение сохраняются при инверсии, 2п линии, соединяющие соответствующие точки исходной цепочки, также проходят через одну точку, О.
Бесконечная семья
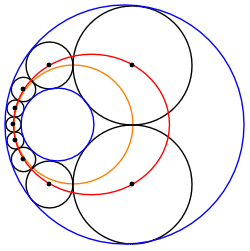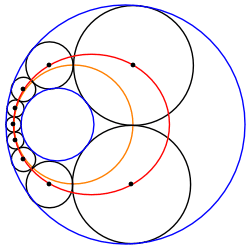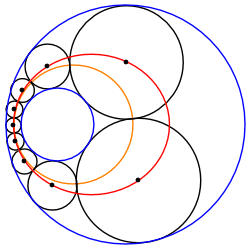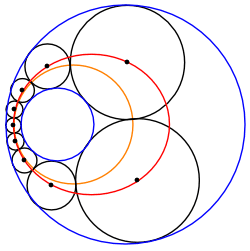
Цепь Штейнера между двумя непересекающимися окружностями всегда может быть преобразована в другую цепочку Штейнера из окружностей одинакового размера, зажатых между двумя концентрическими окружностями. Следовательно, любая такая цепочка Штейнера принадлежит бесконечному семейству цепей Штейнера, связанных поворотом преобразованной цепи вокруг О, общий центр преобразованных ограничивающих кругов.
Эллиптическое / гиперболическое расположение центров
Центры окружностей цепи Штейнера лежат на коническая секция. Например, если меньший заданный круг лежит внутри большего, центры лежат на эллипс. Это верно для любого набора окружностей, которые касаются внутри одной данной окружности и касаются снаружи другой; такие системы кругов появляются в Цепочка паппуса, то проблема Аполлония, а трехмерный Гекслет Содди. Точно так же, если некоторые окружности цепи Штейнера касаются снаружи обеих данных окружностей, их центры должны лежать на гиперболе, тогда как те, которые касаются изнутри обеих окружностей, лежат на другой гиперболе.
Окружности цепи Штейнера касаются двух неподвижных окружностей, обозначенных здесь как α и β, куда β заключен вα. Обозначим радиусы этих двух окружностей как рα и рβсоответственно, а их центрами будут точки А и B. Пусть радиус, диаметр и центральная точка kth окружность цепи Штейнера обозначим как рk, dk и пk, соответственно.
Все центры окружностей в цепочке Штейнера расположены на общем эллипспо следующей причине.[2] Сумма расстояний от центральной точки kth окружность цепи Штейнера к двум центрам А и B неподвижных окружностей равна постоянной
Таким образом, для всех центров окружностей цепи Штейнера сумма расстояний до А и B равно той же константе, рα + рβ. Это определяет эллипс, два фокусы это точки А и B, центры окружностей, α и β, которые сэндвич с цепочкой кругов Штейнера.
Сумма расстояний до фокусов в два раза больше большая полуось а эллипса; следовательно,
Позволять п равное расстояние между очагами, А и B. Затем эксцентриситет е определяется 2 ае = п, или же
По этим параметрам малая полуось б и полу-латусная прямая кишка L можно определить
Следовательно, эллипс можно описать уравнением в терминах расстояния до него. d к одному фокусу
куда θ - угол с линией, соединяющей два фокуса.
Сопряженные цепи
- Сопрягать цепи Штейнера с п = 4
Если цепь Штейнера имеет четное число окружностей, то любые две диаметрально противоположные окружности в цепочке можно рассматривать как две заданные окружности новой цепи Штейнера, которой принадлежат исходные окружности. Если в исходной цепи Штайнера п круги в м оборачивается, а в новой цепочке п круги в q оборачивается, то уравнение выполняется
Простой пример имеет место для цепочек Штейнера из четырех окружностей (п = 4) и один виток (м = 1). В этом случае данные окружности и окружности цепи Штейнера эквивалентны в том смысле, что оба типа окружностей касаются четырех других; в более общем смысле, окружности цепи Штейнера касаются четырех окружностей, но две заданные окружности касаются п круги. В этом случае любая пара противоположных элементов цепи Штейнера может быть выбрана в качестве заданных окружностей другой цепи Штейнера, которая включает исходные заданные кружки. С м = п = 1 и п = q = 4, выполняется уравнение Штейнера:
Обобщения

Простейшее обобщение цепи Штейнера состоит в том, чтобы позволить данным кругам касаться или пересекаться друг с другом. В первом случае это соответствует Цепочка паппуса, имеющий бесконечное количество кругов.
Гекслет Содди является трехмерным обобщением цепочки Штейнера из шести окружностей. Центры шести сфер ( шестиугольник) движутся по тому же эллипсу, что и центры соответствующей цепочки Штейнера. Оболочка гекслет-сфер представляет собой Циклид Дюпена, обращение тор. Шесть сфер касаются не только внутренней и внешней сферы, но и двух других сфер, центрированных выше и ниже плоскости центров гекслетов.
Кратные кольца цепей Штейнера - еще одно обобщение. Обычная цепочка Штейнера получается обращением кольцевой цепочки касательных окружностей, ограниченных двумя концентрическими окружностями. Это можно обобщить на инвертирование трех или более концентрических окружностей, которые образуют кольцевые цепочки касательных окружностей.
Иерархические цепочки Штейнера - еще одно обобщение. Если две заданные окружности обычной цепи Штейнера вложены друг в друга, т. Е. Если одна целиком лежит внутри другой, то данная окружность большего размера описывает окружности цепи Штейнера. В иерархической цепи Штейнера каждый круг цепи Штейнера сам является описывающим данным кругом другой цепи Штейнера внутри нее; этот процесс может повторяться бесконечно, образуя фрактал.
Смотрите также
Рекомендации
Библиография
- Огилви, К.С. (1990). Экскурсии по геометрии. Дувр. стр.51–54. ISBN 0-486-26530-7.
- Кокстер, H.S.M.; Грейцер, С. (1967). Возвращение к геометрии. Новая математическая библиотека. 19. Вашингтон: MAA. С. 123–126, 175–176, 180. ISBN 978-0-88385-619-2. Zbl 0166.16402.
- Джонсон Р.А. (1960). Расширенная евклидова геометрия: элементарный трактат о геометрии треугольника и круга (перепечатка издания 1929 г., изд. Houghton Miflin). Нью-Йорк: Dover Publications. С. 113–115. ISBN 978-0-486-46237-0.
- Уэллс Д. (1991). Словарь любопытной и интересной геометрии Penguin. Нью-Йорк: Книги Пингвинов. стр.244–245. ISBN 0-14-011813-6.
дальнейшее чтение
- Eves H (1972). Обзор геометрии (переработанная ред.). Бостон: Аллин и Бэкон. С. 134–135. ISBN 978-0-205-03226-6.
- Pedoe D (1970). Курс геометрии для колледжей и университетов. Издательство Кембриджского университета. С. 97–101. ISBN 978-0-521-07638-8.
- Кулидж Дж. Л. (1916). Трактат о круге и сфере. Оксфорд: Clarendon Press. С. 31–37.
внешняя ссылка
| Викискладе есть медиафайлы по теме Цепи Штейнера. |
- Вайсштейн, Эрик В. "Штайнер Цепь". MathWorld.
- Интерактивная анимация цепи Штейнера, CodePen
- Интерактивный апплет Майкла Борчердса, показывающего анимацию Цепи Штейнера с переменным количеством кругов, сделанных с помощью GeoGebra.














![{ frac {R} {r}} = 1 + { frac {2 sin theta} {1- sin theta}} = { frac {1+ sin theta} {1- sin theta}} = left [ sec theta + tan theta right] ^ {{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/126fd8aa646cb371dfb8ff48820f52d2c66f2225)

















