WikiDer > Усеченные 24 ячейки - Википедия
 24-элементный | 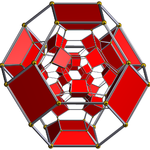 Усеченный 24-элементный |  Урезанный 24-элементный | |
| Диаграммы Шлегеля с центром в одном [3,4] (клетки в противоположных точках в [4,3]) | |||
В геометрия, а усеченный 24-элементный это равномерный 4-многогранник (4-х мерная униформа многогранник) образовалась как усечение регулярного 24-элементный.
Есть две степени усечения, включая битовое усечение.
Усеченный 24-элементный
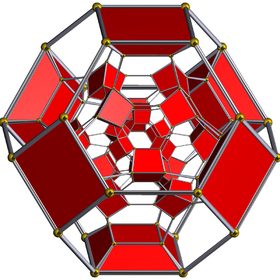 Диаграмма Шлегеля | ||
|---|---|---|
| Усеченный 24-элементный | ||
| Тип | Равномерный 4-многогранник | |
| Символы Шлефли | т {3,4,3} tr {3,3,4} = т {31,1,1} = | |
| Диаграмма Кокстера | ||
| Клетки | 48 | 24 4.6.6 24 4.4.4 |
| Лица | 240 | 144 {4} 96 {6} |
| Края | 384 | |
| Вершины | 192 | |
| Фигура вершины | равносторонняя треугольная пирамида | |
| Группа симметрии | F4 [3,4,3], заказ 1152 | |
| Подгруппа вращения | [3,4,3]+, заказ 576 | |
| Подгруппа коммутатора | [3+,4,3+], заказ 288 | |
| Характеристики | выпуклый | |
| Единый индекс | 23 24 25 | |
В усеченный 24-элементный или же усеченный икозитетрахорон - равномерный 4-мерный многогранник (или равномерный 4-многогранник), что ограничено 48 клетки: 24 кубики, и 24 усеченные октаэдры. Каждая вершина соединяет три усеченных октаэдра и один куб в равностороннюю треугольную пирамиду. вершина фигуры.
Строительство
В усеченный 24-элементный можно построить из многогранников с тремя группами симметрии:
- F4 [3,4,3]: A усечение из 24-элементный.
- B4 [3,3,4]: A усечение из 16 ячеек, с двумя семействами усеченных октаэдрических ячеек.
- D4 [31,1,1]: An омниусечение из demitesseract, с тремя семействами усеченных октаэдрических ячеек.
| Группа Кокстера | = [3,4,3] | = [4,3,3] | = [3,31,1] |
|---|---|---|---|
| Символ Шлефли | т {3,4,3} | tr {3,3,4} | т {31,1,1} |
| Заказ | 1152 | 384 | 192 |
| Полный симметрия группа | [3,4,3] | [4,3,3] | <[3,31,1]> = [4,3,3] [3[31,1,1]] = [3,4,3] |
| Диаграмма Кокстера | |||
| Грани | 3: 1: | 2: 1: 1: | 1,1,1: 1: |
| Фигура вершины | 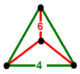 | 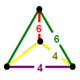 |  |
Зонотоп
Это также зонотоп: он может быть сформирован как Сумма Минковского шести отрезков прямых, соединяющих противоположные пары среди двенадцати перестановок вектора (+ 1, −1,0,0).
Декартовы координаты
В Декартовы координаты вершин усеченной 24-ячейки с длиной ребра sqrt (2) являются перестановками координат и комбинациями знаков:
- (0,1,2,3) [4!×23 = 192 вершины]
Двойственная конфигурация имеет координаты при всех перестановках координат и знаки
- (1,1,1,5) [4×24 = 64 вершины]
- (1,3,3,3) [4×24 = 64 вершины]
- (2,2,2,4) [4×24 = 64 вершины]
Структура
24 кубических ячейки соединены своими квадратными гранями с усеченными октаэдрами; и 24 усеченных октаэдра соединены друг с другом своими шестиугольными гранями.
Прогнозы
Параллельная проекция усеченной 24-ячейки в 3-мерное пространство, сначала усеченный октаэдр, имеет следующую схему:
- Конверт проекции - это усеченный кубооктаэдр.
- Два усеченных октаэдра выступают на усеченный октаэдр, лежащий в центре оболочки.
- Шесть кубовидных объемов соединяют квадратные грани этого центрального усеченного октаэдра с центром восьмиугольных граней большого ромбокубооктаэдра. Это изображения 12 кубических ячеек, по паре ячеек на каждое изображение.
- 12 квадратных граней большого ромбокубооктаэдра являются изображениями остальных 12 кубов.
- Шесть восьмиугольных граней большого ромбокубооктаэдра являются изображениями шести усеченных октаэдров.
- 8 (неоднородных) усеченных октаэдров, лежащих между шестиугольными гранями оболочки проекции и центральным усеченным октаэдром, являются изображениями остальных 16 усеченных октаэдров, пары ячеек для каждого изображения.
Изображений
| Самолет Кокстера | F4 | |
|---|---|---|
| График |  | |
| Двугранная симметрия | [12] | |
| Самолет Кокстера | B3 / А2 (а) | B3 / А2 (б) |
| График |  | 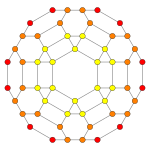 |
| Двугранная симметрия | [6] | [6] |
| Самолет Кокстера | B4 | B2 / А3 |
| График | 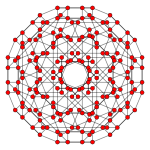 | 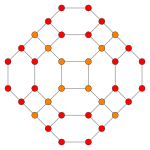 |
| Двугранная симметрия | [8] | [4] |
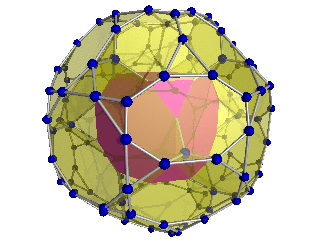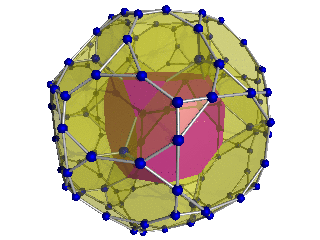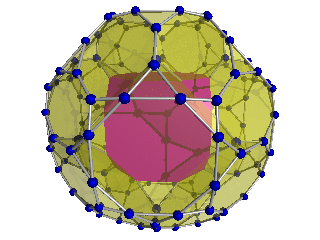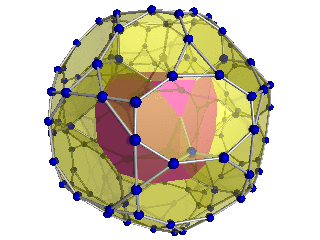
 Диаграмма Шлегеля (кубический ячейки видны) | 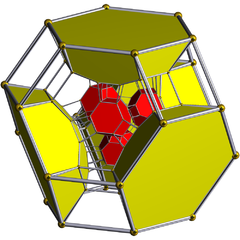 Диаграмма Шлегеля Видны 8 из 24 усеченных октаэдрических ячеек |
 Стереографическая проекция Сосредоточено на усеченный тетраэдр | |
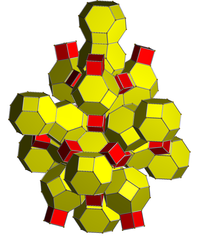 Усеченный 24-элементный |  Двойной на усеченный 24-элементный |
Связанные многогранники
Выпуклая оболочка усеченной 24-клеточной и двойственной ей (в предположении, что они конгруэнтны) представляет собой неоднородный полихорон, состоящий из 480 клеток: 48 кубики, 144 квадратные антипризмы, 288 тетраэдры (как тетрагональные дифеноиды) и 384 вершины. Его вершинная фигура - гексакис треугольный купол.
Урезанный 24-элементный
| Урезанный 24-элементный | ||
|---|---|---|
 Диаграмма Шлегеляс центром на усеченном кубе, чередующиеся ячейки скрыты | ||
| Тип | Равномерный 4-многогранник | |
| Символ Шлефли | 2т {3,4,3} | |
| Диаграмма Кокстера | ||
| Клетки | 48 (3.8.8) | |
| Лица | 336 | 192 {3} 144 {8} |
| Края | 576 | |
| Вершины | 288 | |
| Край фигура | 3.8.8 | |
| Фигура вершины | 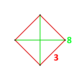 тетрагональный дисфеноид | |
| двойственный многогранник | Дисфеноидальный 288-элементный | |
| Группа симметрии | Aut(F4), [[3,4,3]], заказ 2304 | |
| Характеристики | выпуклый, изогональный, изотоксальный, изохорный | |
| Единый индекс | 26 27 28 | |
В усеченный битами 24 ячейки. 48 ячеек, или же тетраконтоктахорон является 4-мерной однородной многогранник (или же равномерный 4-многогранник) полученный из 24-элементный.
Э. Л. Элте идентифицировал его в 1912 г. как полуправильный многогранник.
Он построен усечение битов 24 ячейки (усечение на полпути до глубины, которая даст двойной 24-ячеечная).
Будучи равномерным 4-многогранником, он вершинно-транзитивный. Кроме того, это клеточно-транзитивный, состоящий из 48 усеченные кубики, а также реберно-транзитивный, с 3 усеченные кубики ячеек на ребро и с одним треугольником и двумя восьмиугольниками по каждому краю.
48 ячеек усеченных битами 24 ячеек соответствуют 24 ячейкам и 24 вершинам 24 ячеек. Таким образом, центры 48 ячеек образуют корневая система типа F4.
Его вершина - фигура тетрагональный дисфеноид, тетраэдр с двумя противоположными ребрами длиной 1 и всеми четырьмя боковыми ребрами длиной √ (2 + √2).
Альтернативные названия
- 24-ячеечная обрезка (Норман В. Джонсон)
- 48 ячеек как клеточно-транзитивный 4-многогранник
- Bitruncated icositetrachoron
- Битроусеченный полиоктаэдр
- Тетраконтаоктахорон (продолжение) (Джонатан Бауэрс)
Структура
Усеченные кубы соединены друг с другом своими восьмиугольными гранями в анти ориентация; я. е., два смежных усеченных куба повернуты на 45 градусов друг относительно друга, так что никакие две треугольные грани не имеют общего ребра.
Последовательность усеченных кубов, соединенных друг с другом противоположными восьмиугольными гранями, образует цикл из 8. Каждый усеченный куб принадлежит 3 таким циклам. С другой стороны, последовательность усеченных кубов, соединенных друг с другом противоположными треугольными гранями, образует цикл из 6. Каждый усеченный куб принадлежит 4 таким циклам.
Видно в матрица конфигурации, показаны все числа случаев между элементами. Диагональ f-вектор числа выводятся через Строительство Wythoff, разделяя полный порядок групп в порядке подгрупп, удаляя по одному зеркалу за раз. Края существуют в 4 положениях симметрии. Квадраты существуют в 3 позициях, шестиугольники - в двух и восьмиугольники - в одной. Наконец, существуют 4 типа ячеек с центрами в 4 углах основного симплекса.[1]
| F4 | k-лицо | жk | ж0 | ж1 | ж2 | ж3 | k-фигура | Примечания | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| А1А1 | ( ) | ж0 | 288 | 2 | 2 | 1 | 4 | 1 | 2 | 2 | с {2,4} | F4/ А1А1 = 288 | |
| { } | ж1 | 2 | 288 | * | 1 | 2 | 0 | 2 | 1 | {} v () | |||
| 2 | * | 288 | 0 | 2 | 1 | 1 | 2 | ||||||
| А2А1 | {3} | ж2 | 3 | 3 | 0 | 96 | * | * | 2 | 0 | { } | F4/ А2А1 = 1152/6/2 = 96 | |
| B2 | т {4} | 8 | 4 | 4 | * | 144 | * | 1 | 1 | F4/ B2 = 1152/8 = 144 | |||
| А2А1 | {3} | 3 | 0 | 3 | * | * | 96 | 0 | 2 | F4/ А2А1 = 1152/6/2 = 96 | |||
| B3 | т {4,3} | ж3 | 24 | 24 | 12 | 8 | 6 | 0 | 24 | * | ( ) | F4/ B3 = 1152/48 = 24 | |
| 24 | 12 | 24 | 0 | 6 | 8 | * | 24 | ||||||
Координаты
В Декартовы координаты усеченной битовой ячейки 24-ячеек с длиной ребра 2 - это все перестановки координат и знака:
- (0, 2+√2, 2+√2, 2+2√2)
- (1, 1+√2, 1+√2, 3+2√2)
Прогнозы
Проекция в 2 измерения
| Самолет Кокстера | F4 | B4 |
|---|---|---|
| График |  | 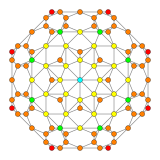 |
| Двугранная симметрия | [[12]] = [24] | [8] |
| Самолет Кокстера | B3 / А2 | B2 / А3 |
| График | 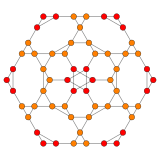 |  |
| Двугранная симметрия | [6] | [[4]] = [8] |
Проекция в 3 измерения
| Орфографический | Перспектива |
|---|---|
Следующая анимация показывает ортогональную проекцию усеченных битами 24-ячеек в 3 измерениях. Сама анимация представляет собой перспективную проекцию из статического 3D-изображения в 2D, с добавленным вращением, чтобы сделать его структуру более очевидной. Образы 48 усеченных кубов выложены следующим образом:
| Следующая анимация показывает перспективную проекцию усеченных битом 24-ячеек в 3-х измерениях. Его структура такая же, как и у предыдущей анимации, за исключением того, что есть ракурс за счет перспективной проекции. |
 |
Связанный правильный косой многогранник
В правильный косой многогранник, {8,4 | 3}, существует в 4-мерном пространстве с четырьмя восьмиугольниками вокруг каждой вершины в зигзагообразной неплоской вершинной фигуре. Эти восьмиугольные грани можно увидеть на усеченных битами 24 ячейках, использующих все 576 ребер и 288 вершин. 192 треугольных грани усеченных битом 24-ячеек можно увидеть как удаленные. Двойственный правильный косой многогранник, {4,8 | 3}, аналогичным образом связан с квадратными гранями многогранника. беглый 24-элементный.
Дисфеноидальный 288-элементный
| Дисфеноидальный 288-элементный | ||
|---|---|---|
| Тип | идеально[2] полихорон | |
| Символ | ж1,2F4[2] (1,0,0,0)F4 ⊕ (0,0,0,1)F4[3] | |
| Coxeter | ||
| Клетки |  288 конгруэнтных тетрагональные дифеноиды | |
| Лица | 576 конгруэнтных равнобедренный (2 коротких края) | |
| Края | 336 | 192 длины 144 длины |
| Вершины | 48 | |
| Фигура вершины |  (Октаэдр Триаки) | |
| Двойной | Урезанный 24-элементный | |
| Группа Кокстера | Aut(F4), [[3,4,3]], заказ 2304 | |
| Вектор орбиты | (1, 2, 1, 1) | |
| Характеристики | выпуклый, изохорный | |
В дисфеноидальный 288-элементный это двойной из усеченный битами 24 ячейки. Это 4-х мерный многогранник (или же полихорон) полученный из 24-элементный. Он создается путем удвоения и вращения 24-элементной ячейки, а затем построения выпуклый корпус.
Являясь двойником однородного полихорона, он клеточно-транзитивный, состоящий из 288 конгруэнтных тетрагональные дифеноиды. Кроме того, это вершинно-транзитивный под группой Aut (F4).[3]
Изображений
| Самолеты Кокстера | B2 | B3 | F4 |
|---|---|---|---|
| Дисфеноидальный 288 ячеек | 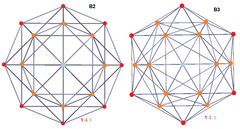 |  | |
| Bitruncated 24-элементный |  | 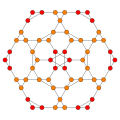 |  |
Геометрия
Вершинами 288-ячеек в точности являются 24 Кватернионы единиц Гурвица с нормой в квадрате 1, объединенной с 24 вершинами двойственной 24-ячейки с нормой в квадрате 2, спроецированной на единицу 3-сфера. Эти 48 вершин соответствуют бинарная октаэдрическая группа, <2,3,4>, заказ 48.
Таким образом, 288-ячейка - единственный нерегулярный 4-многогранник, который является выпуклой оболочкой кватернионной группы, не считая бесконечного множества дициклический (такие же, как бинарные диэдральные) группы; обычные - это 24-элементный (≘ 2Т, <2,3,3>, порядок 24) и 120 ячеек (≘ 2I, <2,3,5>, заказ 120). (The 16 ячеек соответствует бинарная группа диэдра 2D2, <2,2,2>, порядок 16.)
Вписанная 3-сфера имеет радиус 1/2 +√2/ 4 ≈ 0,853553 и касается 288-ячеек в центрах 288 тетраэдров, которые являются вершинами двойных усеченных битами 24-ячеек.
Вершины могут быть окрашен в 2 цвета, скажем, красный и желтый, с 24 единицами Hurwitz красным и 24 двойными желтыми, желтый 24-элементный конгруэнтно красному. Таким образом, продукт 2 одинаково окрашенных кватернионов красный, а продукт 2 смешанных цветов - желтый.
Имеется 192 длинных ребра длиной 1, соединяющих одинаковые цвета, и 144 коротких ребра длины. √2–√2 ≈ 0,765367 соединяющих смешанных цветов. 192 * 2/48 = 8 длинных и 144 * 2/48 = 6 коротких, то есть вместе 14 ребер пересекаются в любой вершине.
576 лиц равнобедренный с 1 длинным и 2 короткими краями, все совпадающие. Углы в основании - arccos (√4+√8/ 4) ≈ 49,210 °. 576 * 3/48 = 36 граней пересекаются в вершине, 576 * 1/192 = 3 на длинном крае и 576 * 2/144 = 8 на коротком.
288 ячеек представляют собой тетраэдры с 4 короткими ребрами и 2 противоположными и перпендикулярными длинными ребрами, одна из которых соединяет 2 красные, а другие 2 желтые вершины. Все клетки конгруэнтны. 288 * 4/48 = 24 клетки встречаются в вершине. 288 * 2/192 = 3 ячейки встречаются на длинном крае, 288 * 4/144 = 8 - на коротком. 288 * 4/576 = 2 ячейки встречаются в треугольнике.
| Область, край | Слой | Широта | красный | желтый |
|---|---|---|---|---|
| Северное полушарие | 3 | 1 | 1 | 0 |
| 2 | √2/2 | 0 | 6 | |
| 1 | 1/2 | 8 | 0 | |
| Экватор | 0 | 0 | 6 | 12 |
| Южное полушарие | –1 | –1/2 | 8 | 0 |
| –2 | –√2/2 | 0 | 6 | |
| –3 | –1 | 1 | 0 | |
| Общий | 24 | 24 |
Поместив фиксированную красную вершину на северном полюсе (1,0,0,0), мы получим 6 желтых вершин на следующей более глубокой «широте» в (√2/ 2, x, y, z), за которым следуют 8 красных вершин по широте в точке (1/2, x, y, z). Следующая более глубокая широта - это гиперплоскость экватора, пересекающая 3-сферу в 2-сфере, которая населена 6 красными и 12 желтыми вершинами.
Слой 2 - это 2-сфера, описывающая правильный октаэдр, ребра которого имеют длину 1. Тетраэдр с вершинным северным полюсом имеет 1 из этих ребер в виде длинного ребра, две вершины которого соединены короткими ребрами с северным полюсом. Еще один длинный край идет от северного полюса в слой 1 и 2 коротких края оттуда в слой 2.
Связанные многогранники
| D4 однородная полихора | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  | ||||
| {3,31,1} ч {4,3,3} | 2r {3,31,1} час3{4,3,3} | т {3,31,1} час2{4,3,3} | 2т {3,31,1} час2,3{4,3,3} | г {3,31,1} {31,1,1}={3,4,3} | рр {3,31,1} г {31,1,1} = г {3,4,3} | tr {3,31,1} т {31,1,1} = t {3,4,3} | sr {3,31,1} с {31,1,1} = s {3,4,3} | ||||
B4 семейство однородных многогранников:
| Многогранники симметрии B4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Имя | тессеракт | исправленный тессеракт | усеченный тессеракт | скошенный тессеракт | разбитый тессеракт | усеченный битами тессеракт | усеченный тессеракт | runcitruncated тессеракт | всесторонне усеченный тессеракт | ||
| Coxeter диаграмма | = | = | |||||||||
| Schläfli символ | {4,3,3} | т1{4,3,3} г {4,3,3} | т0,1{4,3,3} т {4,3,3} | т0,2{4,3,3} рр {4,3,3} | т0,3{4,3,3} | т1,2{4,3,3} 2т {4,3,3} | т0,1,2{4,3,3} tr {4,3,3} | т0,1,3{4,3,3} | т0,1,2,3{4,3,3} | ||
| Шлегель диаграмма |  |  |  |  |  |  |  |  |  | ||
| B4 |  |  |  |  |  |  |  |  |  | ||
| Имя | 16 ячеек | исправленный 16 ячеек | усеченный 16 ячеек | скошенный 16 ячеек | разбитый 16 ячеек | усеченный битами 16 ячеек | усеченный 16 ячеек | runcitruncated 16 ячеек | всесторонне усеченный 16 ячеек | ||
| Coxeter диаграмма | = | = | = | = | = | = | |||||
| Schläfli символ | {3,3,4} | т1{3,3,4} г {3,3,4} | т0,1{3,3,4} т {3,3,4} | т0,2{3,3,4} рр {3,3,4} | т0,3{3,3,4} | т1,2{3,3,4} 2т {3,3,4} | т0,1,2{3,3,4} tr {3,3,4} | т0,1,3{3,3,4} | т0,1,2,3{3,3,4} | ||
| Шлегель диаграмма |  |  |  |  |  |  |  |  |  | ||
| B4 |  |  |  |  |  |  |  |  |  | ||
F4 семейство однородных многогранников:
| 24-элементные семейные многогранники | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Имя | 24-элементный | усеченный 24-элементный | курносый 24-элементный | выпрямленный 24-элементный | наклонный 24-элементный | усеченный битами 24 ячейки | усеченный 24-элементный | беглый 24-элементный | усеченный 24-элементный | комплексно усеченные 24 ячейки | |
| Schläfli символ | {3,4,3} | т0,1{3,4,3} т {3,4,3} | с {3,4,3} | т1{3,4,3} г {3,4,3} | т0,2{3,4,3} рр {3,4,3} | т1,2{3,4,3} 2т {3,4,3} | т0,1,2{3,4,3} tr {3,4,3} | т0,3{3,4,3} | т0,1,3{3,4,3} | т0,1,2,3{3,4,3} | |
| Coxeter диаграмма | |||||||||||
| Шлегель диаграмма |  |  |  |  |  |  |  |  |  |  | |
| F4 |  |  |  |  |  |  |  |  |  |  | |
| B4 |  |  |  |  |  |  |  |  |  |  | |
| B3(а) |  |  |  |  |  |  |  |  |  |  | |
| B3(б) |  |  |  |  |  |  | |||||
| B2 |  |  |  |  |  |  |  |  |  |  | |
Рекомендации
- ^ Клитцинг, Ричард. "o3x4x3o - продолжение".
- ^ а б О совершенных 4-многогранниках Габор Жеве Вклад в алгебру и геометрию, том 43 (2002), № 1, 243-259] Таблица 2, стр. 252
- ^ а б Кватернионное построение многогранников W (F4) с двойственными многогранниками и ветвлением по подгруппам W (B4) и W (B3) × W (A1) Мехмет Коджа 1, Мудхахир Аль-Аджми 2 и Назифе Оздес Коджа 3 Отделение физики, Научный колледж, Университет Султана Кабуса P.O. Box 36, Al-Khoud 123, Muscat, Sultanate of Oman, p.18. 5.7 Двойственный многогранник многогранника (0, 1, 1, 0) F4 = W (F4) (ω2+ ω3)
- H.S.M. Coxeter:
- Калейдоскопы: Избранные произведения Х.С.М. Coxeter, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Документ 23) Х.С.М. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) 559-591]
- (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45]
- Калейдоскопы: Избранные произведения Х.С.М. Coxeter, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [1]
- Норман Джонсон Равномерные многогранники, Рукопись (1991)
- N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. (1966)
- Клитцинг, Ричард. «Четырехмерные однородные многогранники (полихоры)». x3x4o3o = x3x3x4o - тико, o3x4x3o - продолжение
- 3. Выпуклая однородная полихора на основе икоситетрахорона (24-ячеечная) - Модель 24, 27., Георгий Ольшевский.