WikiDer > Усеченный тетраэдр
| Усеченный тетраэдр | |
|---|---|
 (Нажмите здесь, чтобы повернуть модель) | |
| Тип | Архимедово твердое тело Равномерный многогранник |
| Элементы | F = 8, E = 18, V = 12 (χ = 2) |
| Лица по сторонам | 4{3}+4{6} |
| Обозначение Конвея | tT |
| Символы Шлефли | т {3,3} = ч2{4,3} |
| т0,1{3,3} | |
| Символ Wythoff | 2 3 | 3 |
| Диаграмма Кокстера | |
| Группа симметрии | Тd, А3, [3,3], (* 332), порядок 24 |
| Группа вращения | Т, [3,3]+, (332), порядок 12 |
| Двугранный угол | 3-6: 109°28′16′ 6-6: 70°31′44″ |
| Рекомендации | U02, C16, W6 |
| Характеристики | Полурегулярный выпуклый |
 Цветные лица |  3.6.6 (Фигура вершины) |
 Тетраэдр Триаки (двойственный многогранник) |  Сеть |
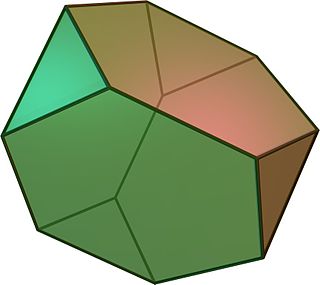
В геометрия, то усеченный тетраэдр является Архимедово твердое тело. Имеет 4 обычных шестиугольник лица, 4 равносторонний треугольник граней, 12 вершин и 18 ребер (двух типов). Его можно построить усечение все 4 вершины регулярного тетраэдр на одну треть исходной длины края.
Более глубокое усечение, удаляющее из каждой вершины тетраэдр с половиной исходной длины ребра, называется исправление. Выпрямление тетраэдра дает октаэдр.[1]
А усеченный тетраэдр это Многогранник Гольдберга граммIII(1,1), содержащие треугольные и шестиугольные грани.
А усеченный тетраэдр можно назвать кантик куб, с Диаграмма Кокстера, ![]()
![]()
![]()
![]()
![]() , имеющий половину вершин скошенного куба (ромбокубооктаэдр),
, имеющий половину вершин скошенного куба (ромбокубооктаэдр), ![]()
![]()
![]()
![]()
![]() . У этой конструкции есть два двойных положения, и их объединение создает униформу. соединение двух усеченных тетраэдров.
. У этой конструкции есть два двойных положения, и их объединение создает униформу. соединение двух усеченных тетраэдров.
Площадь и объем
Площадь А и объем V усеченного тетраэдра реберной длины а находятся:
Самая плотная упаковка
Считается, что наиболее плотной упаковкой архимедова усеченного тетраэдра является Φ =207/208, как сообщили две независимые группы, использующие Методы Монте-Карло.[2][3] Хотя не существует математических доказательств того, что это наилучшая возможная упаковка для усеченного тетраэдра, высокая близость к единству и независимость результатов делают маловероятным обнаружение еще более плотной упаковки. Фактически, если усечение углов немного меньше, чем у усеченного архимедова тетраэдра, эту новую форму можно использовать для полного заполнения пространства.[2]
Декартовы координаты
Декартовы координаты для 12 вершин усеченный тетраэдр с центром в начале координат, с длиной ребра √8, все перестановки (± 1, ± 1, ± 3) с четным числом знаков минус:
- (+3,+1,+1), (+1,+3,+1), (+1,+1,+3)
- (−3,−1,+1), (−1,−3,+1), (−1,−1,+3)
- (−3,+1,−1), (−1,+3,−1), (−1,+1,−3)
- (+3,−1,−1), (+1,−3,−1), (+1,−1,−3)
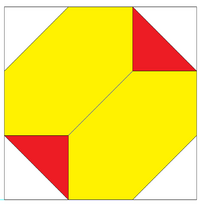 |  |  |
| Ортогональная проекция показывая внутри него декартовы координаты Ограничительная рамка: (±3,±3,±3). | Гексагональные грани усеченных тетраэдров можно разделить на 6 компланарных равносторонних треугольников. 4 новые вершины имеют декартовы координаты: (−1,−1,−1), (−1,+1,+1), (+ 1, −1, + 1), (+ 1, + 1, −1). Как твердое тело это может представлять собой 3D рассечение составляя 4 красных октаэдра и 6 желтых тетраэдров. | Набор перестановок вершин (± 1, ± 1, ± 3) с нечетным числом знаков минус образует дополнительный усеченный тетраэдр, а вместе они образуют однородный составной многогранник. |
Другая простая конструкция существует в 4-пространстве как клетки усеченный 16-элементный, с вершинами как перестановка координат:
- (0,0,1,2)
Ортогональная проекция
| В центре | Край нормальный | Лицо нормальное | Край | Лицо |
|---|---|---|---|---|
| Каркас |  |  |   | |
| Каркас |  |  |  |  |
| Двойной |  |  |  |  |
| Проективный симметрия | [1] | [1] | [4] | [3] |
Сферическая черепица
Усеченный тетраэдр также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Прямые на сфере проецируются как дуги окружности на плоскость.
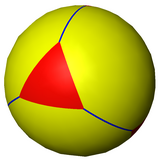 |  треугольник-центрированный |  шестиугольник-центрированный | |
| Ортографическая проекция | Стереографические проекции | ||
|---|---|---|---|
Многогранник Фриауфа
Вариант усеченного тетраэдра с более низкой симметрией (усеченный тетрагональный дисфеноид при заказе 8 D2d симметрии) называется многогранником Фриауфа в таких кристаллах, как сложные металлические сплавы. Эта форма соответствует пяти многогранникам Фриауфа вокруг оси, что дает 72-градусный угол. двугранный угол на подмножестве из 6-6 ребер.[4] Он назван в честь Дж. Б. Фриауф и его статья 1927 г. «Кристаллическая структура интерметаллического соединения MgCu.2".[5]
Использует
Гигантские усеченные тетраэдры были использованы в тематических павильонах «Человек-исследователь» и «Человек-продюсер» в Экспо 67. Они были сделаны из массивных стальных балок, скрепленных болтами в геометрическую решетку. Усеченные тетраэдры соединялись между собой решетчатыми стальными площадками. Все эти здания были снесены после окончания Экспо 67, так как они не были построены, чтобы выдерживать суровые погодные условия Монреаля на протяжении многих лет. Их единственные остатки находятся в городских архивах Монреаля, Государственных архивах Канады и фотоколлекциях туристов того времени.[6]
В Тетраминкс Пазл имеет усеченную четырехгранную форму. Эта головоломка показывает рассечение усеченного тетраэдра на 4 октаэдры и 6 тетраэдры. Он содержит 4 центральные плоскости вращения.
Усеченный тетраэдрический граф
| Усеченный тетраэдрический граф | |
|---|---|
 3-х кратная симметрия | |
| Вершины | 12[7] |
| Края | 18 |
| Радиус | 3 |
| Диаметр | 3[7] |
| Обхват | 3[7] |
| Автоморфизмы | 24 (S4)[7] |
| Хроматическое число | 3[7] |
| Хроматический индекс | 3[7] |
| Характеристики | Гамильтониан, обычный, 3-вершинно-связанный, планарный граф |
| Таблица графиков и параметров | |
в математический поле теория графов, а усеченный тетраэдрический граф является Архимедов граф, то граф вершин и ребер усеченного тетраэдра, один из Архимедовы тела. Имеет 12 вершины и 18 ребер.[8] Это связный кубический граф,[9] и связный кубический транзитивный граф.[10]
| Круговой | Ортографические проекции | |
|---|---|---|
 |  4-х кратная симметрия |  3-х кратная симметрия |
Связанные многогранники и мозаики
| Семейство равномерных тетраэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия: [3,3], (*332) | [3,3]+, (332) | ||||||
 |  |  |  | ||||
| {3,3} | т {3,3} | г {3,3} | т {3,3} | {3,3} | рр {3,3} | tr {3,3} | ср {3,3} |
| Двойники к однородным многогранникам | |||||||
 |  |  |  | ||||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
Он также является частью последовательности кантических многогранников и мозаик с конфигурация вершины 3.6.п.6. В этом Wythoff Construction ребра между шестиугольниками представляют собой вырожденные дигоны.
 | Орбифолд * n32 | Сферический | Евклидово | Гиперболический | Паракомпакт | ||
|---|---|---|---|---|---|---|---|
| *332 | *333 | *433 | *533 | *633... | *∞33 | ||
| Кантическая фигура |  |  |  |  |  |  | |
| Вершина | 3.6.2.6 | 3.6.3.6 | 3.6.4.6 | 3.6.5.6 | 3.6.6.6 | 3.6.∞.6 | |
Мутации симметрии
Этот многогранник топологически связан как часть последовательности равномерных усеченный многогранники с конфигурации вершин (3.2п.2п), и [п,3] Группа Коксетера симметрия.
| *п32 мутация симметрии усеченных сферических мозаик: t {п,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия *п32 [n, 3] | Сферический | Евклид. | Компактная гиперболия. | Paraco. | |||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | ||||
| Усеченный цифры |  |  |  |  |  |  |  | ||||
| Символ | т {2,3} | т {3,3} | т {4,3} | т {5,3} | т {6,3} | т {7,3} | т {8,3} | т {∞, 3} | |||
| Triakis цифры |  |  |  |  |  |  |  | ||||
| Конфиг. | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3.∞.∞ | |||
Примеры
Усеченный тетраэдр (Математека IME-USP)
Смотрите также
- Четвертькубические соты - Заполняет пространство усеченными тетраэдрами и меньшими тетраэдрами
- Усеченный 5-элементный - Подобный однородный многогранник в 4-х измерениях
- Усеченный триакис тетраэдр
- Усеченный тетраэдр Триаки
- Октаэдр - выпрямленный тетраэдр
Рекомендации
- ^ Чисхолм, Мэтт; Авнет, Джереми (1997). «Усеченный обман: усечение». теория.org. Получено 2013-09-02.
- ^ а б Damasceno, Pablo F .; Энгель, Майкл; Глотцер, Шэрон К. (декабрь 2011 г.). «Кристаллические сборки и плотнейшие упаковки семейства усеченных тетраэдров и роль направленных энтропийных сил». САУ Нано. 6 (2012): 609–614. arXiv:1109.1323. Дои:10.1021 / nn204012y. PMID 22098586.
- ^ Цзяо, Ян; Торквато, Сал (сентябрь 2011 г.). «Упаковка усеченных тетраэдров, которая почти заполняет все пространство». arXiv:1107.2300 [cond-mat.soft].
- ^ http://met.iisc.ernet.in/~lord/webfiles/clusters/polyclusters.pdf
- ^ Фриауф, Дж. Б. (1927). «Кристаллическая структура интерметаллида MgCu.2". Варенье. Chem. Soc. 49: 3107–3114. Дои:10.1021 / ja01411a017.
- ^ http://expo67.ncf.ca/man_the_producer_p1.html
- ^ а б c d е ж Атлас графиков, страница = 172, C105
- ^ Атлас графов, стр. 267, усеченный тетраэдрический граф
- ^ Атлас графов, страница 130, связные кубические графы, 12 вершин, C105
- ^ Атлас графов, страница 161, связные кубические транзитивные графы, 12 вершин, Ct11
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X. (Раздел 3-9)
- Читать, R.C .; Уилсон, Р. Дж. (1998), Атлас графиков, Oxford University Press
внешняя ссылка
- Эрик В. Вайсштейн, Усеченный тетраэдр (Архимедово твердое тело) в MathWorld.
- Клитцинг, Ричард. "3D выпуклые равномерные многогранники x3x3o - тут".
- Редактируемая печатная сетка усеченного тетраэдра с интерактивным трехмерным изображением
- Равномерные многогранники
- Многогранники виртуальной реальности Энциклопедия многогранников














































