WikiDer > Додекаэдр с фаской
| Додекаэдр с фаской | |
|---|---|
 | |
| Обозначение Конвея | компакт диск = t5daD = dk5aD |
| Многогранник Гольдберга | гV(2,0) = {5+,3}2,0 |
| Фуллерен | C80[1] |
| Лица | 12 пятиугольники 30 шестиугольники |
| Края | 120 (2 типа) |
| Вершины | 80 (2 типа) |
| Конфигурация вершины | (60) 5.6.6 (20) 6.6.6 |
| Группа симметрии | Икосаэдр (ячас) |
| Двойной многогранник | Пентакис икосододекаэдр |
| Свойства | выпуклый, равностороннийс лицом |
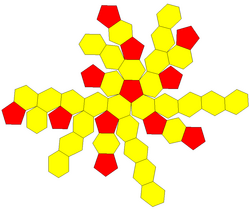 сеть | |
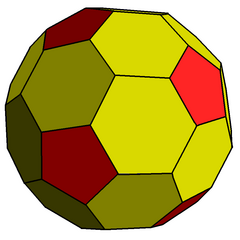
В додекаэдр с фаской это выпуклый многогранник с 80 вершинами, 120 ребрами и 42 гранями: 30 шестиугольников и 12 пятиугольников. Он построен как фаска (геометрия) (усечение края) правильный додекаэдр. Пятиугольники уменьшаются в размере, и вместо всех исходных краев добавляются новые шестиугольные грани. Его двойным является пентакис икосододекаэдр.
Его также называют усеченный ромбический триаконтаэдр, построенный как усечение из ромбический триаконтаэдр. Его точнее можно назвать усеченный ромбический триаконтаэдр порядка 5 потому что только вершины порядка 5 усекаются.
Структура
Эти 12 вершин пятого порядка можно обрезать так, чтобы все ребра были равной длины. Оригинальные 30 ромбический грани становятся неправильными шестиугольниками, а усеченные вершины становятся правильными пятиугольниками.
Грани шестиугольника могут быть равносторонний но нет регулярный с D2 симметрия. Углы в двух вершинах с конфигурация вершины 6.6.6 являются arccos (-1 / sqrt (5)) = 116,565 °, а в оставшихся четырех вершинах с 5.6.6, они составляют 121,717 ° каждая.
Это Многогранник Гольдберга гV(2,0), содержащие пятиугольные и шестиугольные грани.
Он также представляет собой внешнюю оболочку центрированного по ячейке ортогональная проекция из 120 ячеек, один из шести (выпуклые правильные 4-многогранники).
Химия
Это форма фуллерен C80 ; иногда эту фигуру обозначают C80(Ячас), чтобы описать его икосаэдрическую симметрию и отличить его от других менее симметричных 80-вершинных фуллеренов. Это один из четырех фуллеренов, обнаруженных Деза, Деза и Гришухин (1998) иметь скелет который может быть изометрически вложен в L1 Космос.
Связанные многогранники
Этот многогранник очень похож на однородный усеченный икосаэдр который имеет 12 пятиугольников, но только 20 шестиугольников.
Усеченный икосаэдр
G (1,1)клеточно-центрированный ортогональная проекция из 120 ячеек
Додекаэдр с фаской создает больше многогранников за счет основных Обозначения многогранника Конвея. Додекаэдр с фаской на молнии образует усеченный икосаэдр со скошенной фаской и Гольдберг (2,2).
| "семя" | амвон | обрезать | застегивать | расширять | скос | пренебрежительно | фаска | кружиться |
|---|---|---|---|---|---|---|---|---|
 cD = G (2,0) компакт диск |  acD acD |  tcD tcD |  zcD = G (2,2) zcD |  ecD ecD |  bcD bcD |  scD scD |  ccD = G (4,0) ccD |  wcD = G (4,2) туалет |
| двойной | присоединиться | игла | поцелуй | орто | медиальный | гироскоп | двойная фаска | двойной водоворот |
 DCD dcD |  jcD jcD |  NCD NCD |  тыс. канадских долларов тыс. канадских долларов |  ocD ocD |  mcD mcD |  gcD gcD |  dccD dccD |  dwcD dwcD |
Усеченный икосаэдр с фаской
| Усеченный икосаэдр с фаской | |
|---|---|
 | |
| Многогранник Гольдберга | гV(2,2) = {5+,3}2,2 |
| Обозначение Конвея | ctI |
| Фуллерен | C240 |
| Лица | 12 пятиугольники 110 шестиугольники (3 типа) |
| Края | 360 |
| Вершины | 240 |
| Симметрия | ячас, [5,3], (*532) |
| Двойной многогранник | Гексапентакис додекаэдр с фаской |
| Свойства | выпуклый |
В геометрия, то усеченный икосаэдр с фаской это выпуклый многогранник с 240 вершинами, 360 ребрами и 122 гранями, 110 шестиугольниками и 12 пятиугольниками.
Он создается операцией снятия фаски на усеченный икосаэдр, добавляя новые шестиугольники вместо исходных граней. Его также можно построить как операцию zip (= dk = dual of kis of) из додекаэдр с фаской. Другими словами, поднятие пятиугольной и шестиугольной пирамид на додекаэдре со скошенной фаской (операция kis) даст (2,2) геодезический многогранник. Взяв двойное к этому, получаем (2,2) Многогранник Гольдберга, который является усеченным икосаэдром со скошенной фаской, а также Фуллерен C240.
Двойной
Его двойственный, гексапентакид додекаэдр с фаской имеет 240 треугольных граней (сгруппированных как 60 (синие), 60 (красные) вокруг 12 вершин 5-кратной симметрии и 120 вокруг 20 вершин 6-кратной симметрии), 360 ребер и 122 вершины.

Гексапентакис додекаэдр с фаской
использованная литература
- ^ «Изомеры C80». Архивировано из оригинал на 2014-08-12. Получено 2014-08-05.
- Гольдберг, Майкл (1937). «Класс мультисимметричных многогранников». Математический журнал Тохоку. 43: 104–108.
- Харт, Джордж (2012). «Многогранники Гольдберга». В Сенешаль, Марджори (ред.). Формирование пространства (2-е изд.). Springer. стр.125–138. Дои:10.1007/978-0-387-92714-5_9. ISBN 978-0-387-92713-8.
- Харт, Джордж (18 июня 2013 г.). «Математические впечатления: многогранники Гольдберга». Саймонс Новости науки.



