WikiDer > Гиробифастигий удлиненный
| Гиробифастигий удлиненный Остроконечный ромбоэдр | |
|---|---|
 | |
| Тип | Стереоэдр |
| Лица | 4 прямоугольники 4 пятиугольники |
| Края | 18 |
| Вершины | 12 |
| Конфигурация вершины | (4) 4.4.5 (8) 4.5.5 |
| Группа симметрии | D2d, [2+, 4], (2 * 2), порядок 8 |
| Группа вращения | D2, [2,2]+, (222), порядок 4 |
| Двойной многогранник | Курносый дисфеноид |
| Характеристики | выпуклый, заполнение пространства |
| Сеть | |
 | |
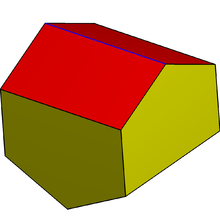
В геометрия, то удлиненный gyrobifastigium или же остроконечный ромбоэдр заполняет пространство октаэдр с 4 прямоугольниками и 4 прямоугольными пятиугольник лица.
Имя
Имя от обычного лица гиробифастигий но удлиненный с 4 треугольниками, расширенными в пятиугольники. Название gyrobifastigium происходит от латинского фастигиум, что означает покатую крышу.[1] В стандартном соглашении об именах Твердые тела Джонсона, би- означает два твердых тела, соединенных их основаниями, и гиро- означает, что две половинки скручены относительно друг друга. Gyrobifastigium является первым в серии гиробикупола, поэтому это твердое тело также можно назвать удлиненно-двуугольные гиробикуполы. Геометрически он также может быть построен как двойник двуугольного гиробиантикупола. Эта конструкция заполняет пространство.
Второе имя, остроконечный ромбоэдр, взято из статьи Майкла Голдберга о заполняющих пространство октаэдрах, модель 8-VI, шестой из по крайней мере 49 заполняющих пространство октаэдров.[2] А фронтон - треугольная часть стены между краями пересекающихся скатов крыши.
Геометрия
Формы высшей симметрии - D2d, порядок 8, а если базовый прямоугольный кубоид искажается в ромбоэдр, симметрия сводится к 2-кратной вращательной симметрии, C2, заказ 2.
Он имеет все 3-валентные вершины и его двойной имеет все треугольные грани, включая курносый дисфеноид как дельтаэдр со всеми равносторонними треугольниками.[3] Однако двойственный курносый дисфеноид не заполняет пространство, потому что пятиугольники не расположены под прямым углом.
Связанные цифры
Удлиненный gyrobifastigium является клеткой изохорный tridecachoron, полихорон, построенный из двойной призмы 13-5 ступеней, который имеет курносый дисфеноид фигура вершины.
Вариации
Топологически отличный удлиненный gyrobifastigium имеет квадратные и равносторонние треугольные грани, обозначенные как 2 треугольные призмы расширен до центрального куб. Это неудачный Джонсон солид за то, что он не строго выпуклый.[4]
Это также многогранник, заполняющий пространство, и он соответствует геометрии гиродлинные треугольные призматические соты если удлиненный gyrobifastigium находятся рассеченный обратно в кубики и треугольные призмы.
 Копланарный квадрат и треугольники |
В удлиненный gyrobifastigium должно быть основано на прямоугольный кубоид или же ромбоэдр для заполнения пространства, при этом угол крыши свободный, в том числе допускающий вогнутые формы. Если крыша имеет нулевой угол, геометрия становится куб или же прямоугольный кубоид.
Пентагоны также можно сделать правильными, а прямоугольники - трапециевидными, и это больше не будет заполнять пространство.
| Тип | Заполнение пространства | Не заполняет пространство | ||||
|---|---|---|---|---|---|---|
| Изображение | 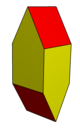 Равносторонние пятиугольники |  Ромбический | 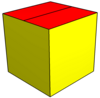 Копланарный |  Вогнутый |  Двойной из курносый дисфеноид | 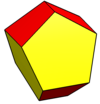 Правильные пятиугольники |
| Сеть |  | 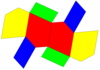 | 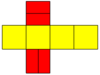 | 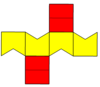 | 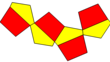 |  |
Соты
Как и gyrobifastigium, он может самотесселяционное пространство. Многогранники мозаичны путем сдвига в плоскости и штабелируются с чередованием ориентации. Сечение многогранника должно быть квадратным или ромбическим, а поперечное сечение крыша угол - свободный, может быть отрицательным, образуя вогнутый многогранник. Ромбические формы требуют, чтобы киральные (зеркальные) многогранные пары заполняли пространство.
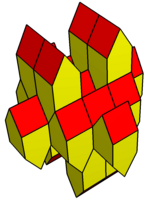 Равносторонний вариант |  Ромбическая вариация | 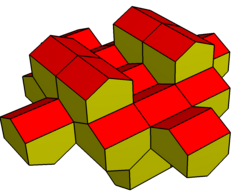 Выпуклая вариация | 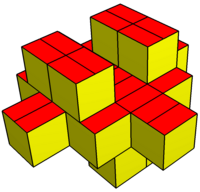 Копланарная вариация | 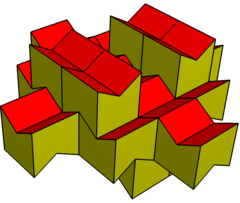 Вогнутый вариант |
Смотрите также
Рекомендации
- ^ Рич, Энтони (1875), "Фастигиум", в Смит, Уильям (ред.), Словарь греческих и римских древностей, Лондон: Джон Мюррей, стр. 523–524..
- ^ Гольдберг, Майкл, О заполняющих пространство октаэдрах, Geometriae Dedicata, январь 1981 г., том 10, выпуск 1, стр. 323–335 [1] PDF В архиве 2017-12-22 в Wayback Machine
- ^ Двойной курносый дисфеноид (J84)
- ^ Выпуклые правильногранные многогранники с условными ребрами P3,2