WikiDer > Дельтаэдр


В геометрии дельтаэдр (множественное число дельтаэдры) это многогранник чей лица все равносторонние треугольники. Название взято из Греческий верхний регистр дельта (Δ), имеющий форму равностороннего треугольника. Дельтаэдров бесконечно много, но из них только восемь. выпуклый, имеющий 4, 6, 8, 10, 12, 14, 16 и 20 граней.[1] Количество граней, ребер и вершины приведен ниже для каждого из восьми выпуклых дельтаэдров.
Восемь выпуклых дельтаэдров
Строго выпуклых дельтаэдров всего восемь: три - правильные многогранники, а пять - Твердые тела Джонсона.
| Правильные дельтаэдры | ||||||
|---|---|---|---|---|---|---|
| Изображение | Имя | Лица | Края | Вершины | Конфигурации вершин | Группа симметрии |
 | тетраэдр | 4 | 6 | 4 | 4 × 33 | Тd, [3,3] |
 | октаэдр | 8 | 12 | 6 | 6 × 34 | Очас, [4,3] |
 | икосаэдр | 20 | 30 | 12 | 12 × 35 | ячас, [5,3] |
| Дельтаэдры Джонсона | ||||||
| Изображение | Имя | Лица | Края | Вершины | Конфигурации вершин | Группа симметрии |
 | треугольная бипирамида | 6 | 9 | 5 | 2 × 33 3 × 34 | D3ч, [3,2] |
 | пятиугольная бипирамида | 10 | 15 | 7 | 5 × 34 2 × 35 | D5ч, [5,2] |
 | курносый дисфеноид | 12 | 18 | 8 | 4 × 34 4 × 35 | D2d, [2,2] |
 | трехугольная призма | 14 | 21 | 9 | 3 × 34 6 × 35 | D3ч, [3,2] |
 | гиродлинная квадратная бипирамида | 16 | 24 | 10 | 2 × 34 8 × 35 | D4d, [4,2] |
В 6-гранном дельтаэдре некоторые вершины имеют степень 3 и некоторую степень 4. В 10-, 12-, 14- и 16-гранном дельтаэдре некоторые вершины имеют степень 4 и некоторую степень 5. Эти пять неправильных дельтаэдров принадлежат к класс Твердые тела Джонсона: выпуклые многогранники с правильные многоугольники для лиц.
Дельтаэдры сохраняют свою форму, даже если ребра могут свободно вращаться вокруг своих вершин, так что углы между ребрами являются плавными. Не все многогранники обладают этим свойством: например, если вы ослабите некоторые углы куб, куб можно деформировать в неправильный квадрат призма.
18-гранного выпуклого дельтаэдра нет.[2] Тем не менее икосаэдр со сжатыми ребрами приводит пример октадекаэдр которые можно сделать выпуклыми с 18 неправильными треугольными гранями или сделать из равносторонних треугольников, которые включают два компланарных набора из трех треугольников.
Нестрого выпуклые случаи
Случаев компланарных треугольников бесконечно много, учитывая сечения бесконечных треугольные мозаики. Если наборы копланарных треугольников считаются одной гранью, можно подсчитать меньший набор граней, ребер и вершин. Копланарные треугольные грани можно объединить в ромбические, трапециевидные, шестиугольные или другие равносторонние многоугольники. Каждое лицо должно быть выпуклым. полиалмаз Такие как ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() , ...[3]
, ...[3]
Вот несколько небольших примеров:
| Изображение | Имя | Лица | Края | Вершины | Конфигурации вершин | Группа симметрии |
|---|---|---|---|---|---|---|
 | Расширенный октаэдр Увеличение 1 тет + 1 окт | 10 | 15 | 7 | 1 × 33 3 × 34 3 × 35 0 × 36 | C3в, [3] |
| 4 3 | 12 | |||||
 | Тригональный трапецоэдр Увеличение 2 тет + 1 окт | 12 | 18 | 8 | 2 × 33 0 × 34 6 × 35 0 × 36 | C3в, [3] |
| 6 | 12 | |||||
 | Увеличение 2 тет + 1 окт | 12 | 18 | 8 | 2 × 33 1 × 34 4 × 35 1 × 36 | C2v, [2] |
| 2 2 2 | 11 | 7 | ||||
 | Усеченный треугольник Увеличение 3 тета + 1 окт. | 14 | 21 | 9 | 3 × 33 0 × 34 3 × 35 3 × 36 | C3в, [3] |
| 1 3 1 | 9 | 6 | ||||
 | Удлиненный октаэдр Увеличение 2 тет + 2 окта | 16 | 24 | 10 | 0 × 33 4 × 34 4 × 35 2 × 36 | D2ч, [2,2] |
| 4 4 | 12 | 6 | ||||
 | Тетраэдр Увеличение 4 тета + 1 окт. | 16 | 24 | 10 | 4 × 33 0 × 34 0 × 35 6 × 36 | Тd, [3,3] |
| 4 | 6 | 4 | ||||
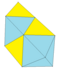 | Увеличение 3 тет + 2 окта | 18 | 27 | 11 | 1 × 33 2 × 34 5 × 35 3 × 36 | D2ч, [2,2] |
| 2 1 2 2 | 14 | 9 | ||||
 | Икосаэдр со сжатием ребер | 18 | 27 | 11 | 0 × 33 2 × 34 8 × 35 1 × 36 | C2v, [2] |
| 12 2 | 22 | 10 | ||||
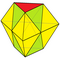 | Двустворчатый треугольный Увеличение 6 тет + 2 окта | 20 | 30 | 12 | 0 × 33 3 × 34 6 × 35 3 × 36 | D3ч, [3,2] |
| 2 6 | 15 | 9 | ||||
 | треугольный купол Увеличение 4 тет + 3 окта | 22 | 33 | 13 | 0 × 33 3 × 34 6 × 35 4 × 36 | C3в, [3] |
| 3 3 1 1 | 15 | 9 | ||||
 | Треугольная бипирамида Увеличение 8 тет + 2 окта | 24 | 36 | 14 | 2 × 33 3 × 34 0 × 35 9 × 36 | D3ч, [3] |
| 6 | 9 | 5 | ||||
 | Шестиугольная антипризма | 24 | 36 | 14 | 0 × 33 0 × 34 12 × 35 2 × 36 | D6d, [12,2+] |
| 12 2 | 24 | 12 | ||||
 | Усеченный тетраэдр Увеличение 6 тет + 4 окта | 28 | 42 | 16 | 0 × 33 0 × 34 12 × 35 4 × 36 | Тd, [3,3] |
| 4 4 | 18 | 12 | ||||
 | Кубооктаэдр Тетракиса Октаэдр Увеличение 8 тет + 6 окт | 32 | 48 | 18 | 0 × 33 12 × 34 0 × 35 6 × 36 | Очас, [4,3] |
| 8 | 12 | 6 |
Невыпуклые формы
Существует бесконечное количество невыпуклых форм.
Некоторые примеры дельтаэдров, пересекающих грани:
- Большой икосаэдр - а Твердое тело Кеплера-Пуансо, с 20 пересекающимися треугольниками
Другие невыпуклые дельтаэдры могут быть созданы путем добавления равносторонних пирамид к граням всех 5 правильных многогранников:
 |  | 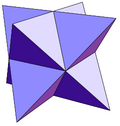 |  |  |
| триакис тетраэдр | тетракис шестигранник | триакис октаэдр (Stella Octangula) | пентакид додекаэдр | триакис икосаэдр |
|---|---|---|---|---|
| 12 треугольников | 24 треугольника | 60 треугольников | ||
Другие увеличения тетраэдра включают:
 |  |  |
| 8 треугольников | 10 треугольников | 12 треугольников |
|---|
Также добавив перевернутые пирамиды к граням:
 Раскопанный додекаэдр |  А тороидальный дельтаэдр |
| 60 треугольников | 48 треугольников |
|---|
Смотрите также
- Симплициальный многогранник - многогранники со всеми симплекс грани
Рекомендации
- ^ Фройденталь, H; ван дер Варден, Б. Л. (1947), «Над een bewering van Euclide (« Об утверждении Евклида »)», Саймон Стевин (на голландском), 25: 115–128 (Они показали, что выпуклых дельтаэдров всего 8.)
- ^ Тригг, Чарльз В. (1978), «Бесконечный класс дельтаэдров», Математический журнал, 51 (1): 55–57, Дои:10.1080 / 0025570X.1978.11976675, JSTOR 2689647.
- ^ Выпуклые дельтаэдры и учет копланарных граней.
дальнейшее чтение
- Раузенбергер, О. (1915), "Konvexe pseudoreguläre Polyeder", Zeitschrift für Mathematischen und naturwissenschaftlichen Unterricht, 46: 135–142.
- Канди, Х. Мартин (Декабрь 1952 г.), «Дельтаэдры», Математический вестник, 36: 263–266, Дои:10.2307/3608204, JSTOR 3608204.
- Канди, Х. Мартин; Роллетт, А. (1989), «3.11. Дельтаэдры», Математические модели (3-е изд.), Stradbroke, England: Tarquin Pub., Стр. 142–144..
- Гарднер, Мартин (1992), Фрактальная музыка, гиперкарты и многое другое: математические развлечения от Scientific American, Нью-Йорк: В. Х. Фриман, стр. 40, 53 и 58-60..
- Пью, Энтони (1976), Многогранники: визуальный подход, Калифорния: Калифорнийский университет Press в Беркли, ISBN 0-520-03056-7 стр. 35–36
