WikiDer > Метод конечных разностей - Википедия
Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|
| Дифференциальные уравнения | |||||
|---|---|---|---|---|---|
 Дифференциальные уравнения Навье – Стокса. используется для имитации воздушного потока вокруг препятствия. | |||||
| Классификация | |||||
Типы
| |||||
Отношение к процессам | |||||
| Решение | |||||
Существование и уникальность | |||||
Методы решения | |||||
В числовой анализ, конечно-разностные методы (FDM) представляют собой класс численных методов решения дифференциальные уравнения приближая производные с конечные разности. И пространственная область, и временной интервал (если применимо) являются дискретизированный, или разбивается на конечное число шагов, и значение решения в этих дискретных точках аппроксимируется путем решения алгебраических уравнений, содержащих конечные разности и значения из близлежащих точек.
Конвертация методов конечных разностей обыкновенные дифференциальные уравнения (ODE) или уравнения в частных производных (PDE), который может быть нелинейный, в система линейных уравнений это может быть решено методами матричной алгебры. Современные компьютеры могут выполнять эти линейная алгебра вычислений, которые, наряду с их относительной простотой реализации, привели к широкому использованию FDM в современном численном анализе.[1]Сегодня FDM являются одним из наиболее распространенных подходов к численному решению PDE, наряду с методы конечных элементов.[1]
Вывод из полинома Тейлора
Во-первых, предполагая, что функция, производные которой должны быть аппроксимированы, ведет себя правильно, Теорема Тейлора, мы можем создать Серия Тейлор расширение
куда п! обозначает факториал из п, и рп(Икс) - остаточный член, обозначающий разницу между полиномом Тейлора степени п и исходная функция. Мы получим приближение для первой производной функции "f", сначала усекая многочлен Тейлора:
Настройка, x0= a имеем,
Разделение на час дает:
Решение для f '(a):
При условии, что достаточно мало, аппроксимация первой производной от "f" равна:
Это не случайно похоже на определение производной, которое дается как:
за исключением предела к нулю (метод назван в честь этого).
Точность и порядок
Погрешность решения метода определяется как разница между приближением и точным аналитическим решением. Двумя источниками ошибок в методах конечных разностей являются: ошибка округления, потеря точности из-за компьютерного округления десятичных величин, и ошибка усечения или же ошибка дискретизации, разница между точным решением исходного дифференциального уравнения и точной величиной при условии точной арифметики (то есть без округления).
Чтобы использовать метод конечных разностей для аппроксимации решения проблемы, необходимо сначала дискретизировать область проблемы. Обычно это делается путем разделения домена на однородную сетку (см. Изображение справа). Это означает, что конечно-разностные методы производят наборы дискретных численных приближений производной, часто «ступенчато по времени».
Выражением всеобщего интереса является локальная ошибка усечения метода. Обычно выражается с помощью Обозначение Big-O, локальная ошибка усечения относится к ошибке из-за одного применения метода. То есть это количество если относится к точному значению и в численном приближении. Остаточный член полинома Тейлора удобен для анализа локальной ошибки усечения. Используя форму Лагранжа остатка от полинома Тейлора для , который
, куда ,
может быть обнаружен доминирующий член локальной ошибки усечения. Например, снова используя формулу прямой разности для первой производной, зная, что ,
и с некоторыми алгебраическими манипуляциями это приводит к
и далее отмечая, что величина слева является приближением метода конечных разностей и что величина справа является точной величиной, представляющей интерес, плюс остаток, ясно, что остаток является локальной ошибкой усечения. Окончательное выражение этого примера и его порядок:
Это означает, что в этом случае локальная ошибка усечения пропорциональна размерам шага. Качество и продолжительность моделируемого решения FDM зависит от выбора уравнения дискретизации и размеров шага (временные и пространственные шаги). Качество данных и продолжительность моделирования значительно увеличиваются при меньшем размере шага.[2] Следовательно, для практического использования необходим разумный баланс между качеством данных и продолжительностью моделирования. Большие временные шаги полезны для увеличения скорости моделирования на практике. Однако слишком большие временные шаги могут создать нестабильность и повлиять на качество данных.[3][4]
В фон Нейман и Курант-Фридрихс-Леви критерии часто оцениваются для определения устойчивости численной модели.[3][4][5][6]
Пример: обыкновенное дифференциальное уравнение
Например, рассмотрим обыкновенное дифференциальное уравнение
В Метод Эйлера для решения этого уравнения используется коэффициент конечных разностей
чтобы аппроксимировать дифференциальное уравнение, сначала подставив его вместо u '(x), затем применив небольшую алгебру (умножив обе части на h, а затем добавив u (x) к обеим сторонам), чтобы получить
Последнее уравнение является конечно-разностным уравнением, и решение этого уравнения дает приближенное решение дифференциального уравнения.
Пример: уравнение теплопроводности
Рассмотрим нормализованный уравнение теплопроводности в одном измерении, с однородным Граничные условия Дирихле
- (граничное условие)
- (начальное состояние)
Один из способов численного решения этого уравнения - аппроксимировать все производные конечными разностями. Разделим область в пространстве сеткой и вовремя используя сетку . Мы предполагаем однородное разделение как в пространстве, так и во времени, поэтому разница между двумя последовательными точками пространства будет час и между двумя последовательными моментами времени будет k. Точки
будет представлять собой численное приближение
Явный метод
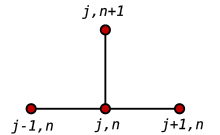
Используя форвардная разница вовремя и второго порядка центральная разница для пространственной производной в позиции (FTCS) получаем рекуррентное уравнение:
Это явный метод для решения одномерной уравнение теплопроводности.
Мы можем получить от других значений таким образом:
куда
Итак, с этим рекуррентным соотношением и зная значения во время п, можно получить соответствующие значения в момент времени п+1. и необходимо заменить граничными условиями, в этом примере они оба равны 0.
Этот явный метод известен как численно стабильный и сходящийся в любое время .[7] Численные ошибки пропорциональны шагу по времени и квадрату шага по пространству:
Неявный метод
Если мы используем обратная разница вовремя и центральная разность второго порядка для пространственной производной в позиции (Обратное время, метод центрированного пространства "BTCS") мы получаем рекуррентное уравнение:
Это неявный метод для решения одномерного уравнение теплопроводности.
Мы можем получить от решения системы линейных уравнений:
Схема всегда численно стабильный и сходящийся, но обычно более интенсивный в числовом отношении, чем явный метод, поскольку он требует решения системы численных уравнений на каждом временном шаге. Ошибки линейны по временному шагу и квадратичны по пространственному шагу:
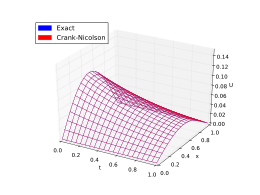
Метод Кранка – Николсона
Наконец, если мы используем центральную разницу во времени и центральная разность второго порядка для пространственной производной в позиции («CTCS») получаем рекуррентное уравнение:
Эта формула известна как Метод Кранка – Николсона.
Мы можем получить от решения системы линейных уравнений:
Схема всегда численно стабильный и сходящийся, но обычно более интенсивный в числовом отношении, поскольку требует решения системы числовых уравнений на каждом временном шаге. Ошибки квадратичны как по временному, так и по пространственному шагу:
Сравнение
Подводя итог, обычно схема Кранка – Николсона является наиболее точной схемой для малых шагов по времени. Для больших временных шагов неявная схема работает лучше, поскольку она менее требовательна к вычислениям. Явная схема наименее точна и может быть нестабильной, но также является наиболее простой в реализации и наименее трудоемкой.
Вот пример. На рисунках ниже представлены решения, полученные с помощью вышеуказанных методов для аппроксимации уравнения теплопроводности.
с граничным условием
Точное решение
Пример: оператор Лапласа
(Непрерывный) Оператор Лапласа в -размеры задаются Дискретный оператор Лапласа зависит от размера .
В 1D оператор Лапласа аппроксимируется как
Это приближение обычно выражается следующим образом: трафарет
и который представляет собой симметричную трехдиагональную матрицу. Для равноудаленной сетки получается Матрица Теплица.
2D-случай показывает все характеристики более общего nD-случая. Каждую вторую частную производную необходимо аппроксимировать аналогично одномерному случаю.
который обычно дается следующим трафарет
Последовательность
Согласованность вышеупомянутого приближения может быть продемонстрирована для очень регулярных функций, таких как Заявление
Чтобы доказать это, нужно заменить Серия Тейлор разложения до порядка 3 в дискретный оператор Лапласа.
Характеристики
Субгармоника
Похожий на непрерывные субгармонические функции можно определить субгармонические функции для конечно-разностных приближений
Среднее значение
Можно определить общий трафарет из положительный тип через
Если является (дискретной) субгармонической, то следующая свойство среднего значения держит
где аппроксимация оценивается по точкам сетки, а шаблон считается положительным.
Похожий свойство среднего значения верно и для непрерывного случая.
Принцип максимума
Для (дискретной) субгармонической функции следующее имеет место
куда являются дискретизацией непрерывной области , соответственно граница .
Похожий принцип максимума справедливо и для непрерывного случая.
Метод SBP-SAT
Метод SBP-SAT - это стабильный и точный метод дискретизации и наложения граничных условий корректного уравнения в частных производных с использованием конечных разностей высокого порядка.[8][9] Метод основан на конечных разностях, где операторы дифференцирования проявляют свойства суммирования по частям. Обычно эти операторы состоят из матриц дифференцирования с центральными разностными шаблонами внутри с тщательно подобранными односторонними граничными шаблонами, предназначенными для имитации интеграции по частям в дискретной настройке. Используя метод SAT, граничные условия PDE накладываются слабо, когда граничные значения «подтягиваются» к желаемым условиям, а не точно выполняются. Если параметры настройки (присущие методике SAT) выбраны правильно, результирующая система ODE будет демонстрировать такое же энергетическое поведение, что и непрерывное PDE, то есть система не имеет роста нефизической энергии. Это гарантирует стабильность, если используется схема интегрирования с областью устойчивости, которая включает части мнимой оси, например метод Рунге-Кутта четвертого порядка. Это делает метод SAT привлекательным методом наложения граничных условий для методов конечных разностей более высокого порядка, в отличие, например, от метода впрыска, который обычно не будет устойчивым, если используются операторы дифференцирования высокого порядка.
Смотрите также
- Метод конечных элементов
- Конечная разница
- Конечная разница во временной области
- Метод бесконечных разностей
- Трафарет (численный анализ)
- Конечно-разностные коэффициенты
- Пятиточечный трафарет
- Теорема Лакса – Рихтмайера
- Конечно-разностные методы ценообразования опционов
- Схема дифференцирования против ветра для конвекции
- Центральная разностная схема
- Дискретное уравнение Пуассона
- Дискретный оператор Лапласа
Рекомендации
- ^ а б Кристиан Гроссманн; Hans-G. Roos; Мартин Стайнс (2007). Численное рассмотрение дифференциальных уравнений в частных производных. Springer Science & Business Media. п.23. ISBN 978-3-540-71584-9.
- ^ Арье Изерлес (2008). Первый курс численного анализа дифференциальных уравнений. Издательство Кембриджского университета. п.23. ISBN 9780521734905.
- ^ а б Hoffman JD; Франкель С (2001). Численные методы для инженеров и ученых. CRC Press, Бока-Ратон.
- ^ а б Jaluria Y; Атлури С (1994). «Расчетная теплопередача». Вычислительная механика. 14: 385–386. Дои:10.1007 / BF00377593.
- ^ Маджумдар П. (2005). Расчетные методы тепломассопереноса (1-е изд.). Тейлор и Фрэнсис, Нью-Йорк.
- ^ Смит Г.Д. (1985). Численное решение уравнений в частных производных: методы конечных разностей (3-е изд.). Издательство Оксфордского университета.
- ^ Крэнк, Дж. Математика диффузии. 2-е издание, Оксфорд, 1975, с. 143.
- ^ Бо Стрэнд (1994). Суммирование по частям для конечно-разностных приближений для d / dx. Журнал вычислительной физики. Дои:10.1006 / jcph.1994.1005.
- ^ Марк Х. Карпентер; Дэвид И. Готтлиб; Саул С. Абарбанель (1994). Устойчивые во времени граничные условия для разностных схем, решающих гиперболические системы: методология и приложение к компактным схемам высокого порядка. Журнал вычислительной физики. Дои:10.1006 / jcph.1994.1057.
дальнейшее чтение
- К.В. Мортон и Д.Ф. Майерс, Численное решение дифференциальных уравнений с частными производными, введение. Издательство Кембриджского университета, 2005.
- Autar Kaw и E. Eric Kalu, Численные методы с приложениями, (2008) [1]. Содержит краткое инженерное введение в FDM (для ODE) в Глава 08.07.
- Джон Стрикверда (2004). Конечно-разностные схемы и уравнения с частными производными (2-е изд.). СИАМ. ISBN 978-0-89871-639-9.
- Смит, Г. Д. (1985), Численное решение дифференциальных уравнений с частными производными: конечно-разностные методы, 3-е изд., Oxford University Press
- Питер Олвер (2013). Введение в уравнения с частными производными. Springer. Глава 5: Конечные различия. ISBN 978-3-319-02099-0..
- Рэндалл Дж. Левек, Конечно-разностные методы для обыкновенных и дифференциальных уравнений с частными производными, СИАМ, 2007.