WikiDer > Маятник
А маятник это груз, подвешенный к вращаться так что он может свободно качаться.[1] Когда маятник смещается в сторону от положения покоя, положение равновесия, это подлежит восстанавливающая сила из-за сила тяжести это ускорит его возврат к положению равновесия. При отпускании восстанавливающая сила, действующая на массу маятника, заставляет его колебаться о положении равновесия, качаясь вперед-назад. Время для одного полного цикла, поворота влево и поворота вправо, называется временем период. Период зависит от длины маятника, а также в небольшой степени от амплитуда, ширина качания маятника.
Из первых научных исследований маятника около 1602 г. Галилео ГалилейРегулярное движение маятников использовалось для хронометража и было самой точной технологией в мире до 1930-х годов.[2] В маятниковые часы изобретен Кристиан Гюйгенс в 1658 году стал мировым стандартным хронометром, который использовался в домах и офисах в течение 270 лет и достиг точности около одной секунды в год, прежде чем он был заменен стандартом времени. кварцевые часы в 1930-е гг. Маятники также используются в научные инструменты Такие как акселерометры и сейсмометры. Исторически они использовались как гравиметры измерить ускорение свободного падения в геофизических исследованиях и даже в качестве эталона длины. Слово «маятник» новая латынь, от латинского маятник, что означает «висит».[3]
Простой гравитационный маятник
В простой гравитационный маятник[4] представляет собой идеализированную математическую модель маятника.[5][6][7] Это гиря (или боб) на конце безмассового шнура, подвешенного к вращаться, без трение. При первоначальном толчке он будет раскачиваться вперед и назад с постоянной амплитуда. Настоящие маятники подвержены трению и сопротивление воздуха, поэтому амплитуда их колебаний уменьшается.
Период колебаний
Период качания простой гравитационный маятник зависит от его длина, местный сила тяжести, и в небольшой степени на максимуме угол что маятник отклоняется от вертикали, θ0, называется амплитуда.[8] Это не зависит от масса боба. Если амплитуда ограничена небольшими колебаниями,[Примечание 1] в период Т простого маятника время, необходимое для полного цикла, составляет:[9]
куда - длина маятника и местный ускорение свободного падения.
Для небольших качелей период качания примерно одинаков для качелей разного размера: то есть период не зависит от амплитуды. Это свойство, называемое изохронизм, вот почему маятники так удобны для хронометража.[10] Последовательные колебания маятника, даже если они меняются по амплитуде, занимают одинаковое время.
Для большего амплитуды, период постепенно увеличивается с амплитудой, поэтому он больше, чем определяется уравнением (1). Например, при амплитуде θ0 = 0,4 радиана (23 °), это на 1% больше, чем указано в (1). Период увеличивается асимптотически (до бесконечности) как θ0 подходы радиан (180 °), потому что значение θ0 = является точка неустойчивого равновесия для маятника. Истинный период идеального простого гравитационного маятника можно записать в нескольких различных формах (см. Маятник (математика) ), одним из примеров является бесконечная серия:[11][12]
куда в радианах.
Разница между этим истинным периодом и периодом небольших колебаний (1) выше называется круговая ошибка. В случае типичного дедушкины часы маятник которого имеет качание 6 ° и, следовательно, амплитуду 3 ° (0,05 радиана), разница между истинным периодом и приближением малого угла (1) составляет около 15 секунд в день.
Для небольших колебаний маятник приближается к гармонический осциллятор, и его движение как функция времени, т, примерно простые гармонические колебания:[5]
куда постоянное значение, зависящее от первоначальные условия.
Для реальных маятников период незначительно меняется в зависимости от таких факторов, как плавучесть и вязкое сопротивление воздуха, масса струны или стержня, размер и форма боба, а также способ его крепления к струне, а также гибкость и растяжение струны. Струна.[11][13] В точных приложениях, возможно, потребуется применить поправки к этим факторам к ур. (1) точно указать период.
Составной маятник
Любое качание жесткое тело свободное вращение вокруг фиксированной горизонтальной оси называется составной маятник или же физический маятник. Соответствующая эквивалентная длина для расчета периода любого такого маятника - это расстояние от оси до центр колебаний.[14] Эта точка находится под центр массы На расстоянии от оси вращения традиционно называется радиус колебания, который зависит от распределения массы маятника. Если большая часть массы сосредоточена в относительно небольшом бобе по сравнению с длиной маятника, центр колебаний находится близко к центру масс.[15]
Радиус колебаний или эквивалентная длина любого физического маятника можно показать как
куда это момент инерции маятника вокруг точки поворота, - масса маятника, а это расстояние между точкой поворота и центр массыПодставляя это выражение в (1) выше, период составного маятника определяется выражением
для достаточно малых колебаний.[16]
Например, жесткий равномерный стержень длиной вращается вокруг одного конца, имеет момент инерции .Центр масс находится в центре стержня, поэтому Подстановка этих значений в приведенное выше уравнение дает . Это показывает, что маятник с жестким стержнем имеет тот же период, что и простой маятник, на 2/3 его длины.
Кристиан Гюйгенс в 1673 году доказал, что точка поворота и центр колебаний взаимозаменяемы.[17] Это означает, что если какой-либо маятник перевернуть вверх дном и качнуть от оси, расположенной в его предыдущем центре колебаний, он будет иметь тот же период, что и раньше, а новый центр колебаний будет в старой точке поворота. В 1817 г. Генри Катер использовал эту идею для создания типа обратимого маятника, теперь известного как Катер маятник, для улучшенных измерений ускорения свободного падения.
История
Одним из первых известных применений маятника был 1-й век. сейсмометр устройство династия Хан Китайский ученый Чжан Хэн.[18] Его функция заключалась в том, чтобы раскачивать и активировать один из ряда рычагов после того, как его потревожила тремор землетрясение далеко.[19] Небольшой шарик, выпущенный рычагом, выпадал из устройства в форме урны в одну из восьми металлических пастей жаб внизу, в восьми точках компаса, указывая направление землетрясения.[19]
Многие источники[20][21][22][23] утверждают, что египетский астроном 10 века Ибн Юнус использовал маятник для измерения времени, но это была ошибка, возникшая в 1684 году британским историком Эдвард Бернард.[24][25][26]
Вовремя эпоха Возрождениябольшие маятники с ручной накачкой использовались в качестве источников энергии для ручных поршневых машин, таких как пилы, сильфоны и насосы.[27] Леонардо да Винчи сделал много рисунков движения маятников, хотя и не осознавал его ценности для хронометража.
1602: Исследования Галилея
Итальянский ученый Галилео Галилей был первым, кто изучал свойства маятников, начиная примерно с 1602 года.[28] Самый ранний дошедший до нас отчет о его исследованиях содержится в письме Гвидо Убальдо дал Монте из Падуи от 29 ноября 1602 года.[29] Его биограф и ученик, Винченцо Вивиани, утверждал, что его интерес возник примерно в 1582 году из-за раскачивания люстры в Пизанский собор.[30][31] Галилей открыл важнейшее свойство, которое делает маятники полезными для хронометража, - изохронизм; период маятника примерно не зависит от амплитуда или ширину качелей.[32] Он также обнаружил, что период не зависит от масса боба, и пропорционально квадратный корень длины маятника. Он первым применил маятники со свободным покачиванием в простых приложениях для измерения времени. Его друг врач, Санторио Сантори, изобрел прибор, который измерял пульс по длине маятника; в пульсилогиум.[28] В 1641 году Галилей продиктовал своему сыну Винченцо конструкция для маятниковых часов;[32] Винченцо начал строительство, но не завершил его, когда умер в 1649 году.[33] Маятник был первым гармонический осциллятор используется человеком.[32][требуется разъяснение]
1656: Маятниковые часы
В 1656 г. голландский ученый Кристиан Гюйгенс построил первый маятниковые часы.[34] Это было большим улучшением по сравнению с существующими механическими часами; их лучшая точность была улучшена с отклонения примерно с 15 минут в день до примерно 15 секунд в день.[35] Маятники распространились по Европе, поскольку существующие часы были модернизированный с ними.[36]
Английский ученый Роберт Гук изучил конический маятник около 1666 г., состоящий из маятника, который может свободно качаться в двух измерениях, с бобом, вращающимся по кругу или эллипсу.[37] Он использовал движения этого устройства в качестве модели для анализа орбитальные движения из планеты.[38] Гук предложил Исаак Ньютон в 1679 году, компоненты орбитального движения состояли из движения по инерции в касательном направлении и движения притяжения в радиальном направлении. Это сыграло роль в формулировке Ньютоном закон всемирного тяготения.[39][40] Роберт Гук также был ответственен за предположение еще в 1666 году, что маятник можно использовать для измерения силы тяжести.[37]
Во время его экспедиции в Cayenne, Французская Гвиана в 1671 г., Жан Рише обнаружил, что маятниковые часы был2 1⁄2 минут в день медленнее в Cayenne, чем в Париже. Из этого он сделал вывод, что на Кайенне сила тяжести была ниже.[41][42] В 1687 г. Исаак Ньютон в Principia Mathematica показал, что это произошло потому, что Земля не была настоящей сферой, а слегка сплюснутый (сплюснутые на полюсах) от воздействия центробежная сила из-за его вращения, в результате чего сила тяжести увеличивается с широта.[43] Переносные маятники стали брать в дальние путешествия, как точность. гравиметры измерить ускорение свободного падения в разных точках Земли, что в конечном итоге привело к созданию точных моделей форма Земли.[44]
1673: Гюйгенс Часы Oscillatorium
В 1673 году, через 17 лет после изобретения маятниковых часов, Кристиан Гюйгенс опубликовал свою теорию маятника, Часы Oscillatorium sive de motu pendulorum.[45][46] Марин Мерсенн и Рене Декарт около 1636 г. обнаружил, что маятник не совсем изохронен; его период несколько увеличивался с увеличением амплитуды.[47] Гюйгенс проанализировал эту проблему, определив, по какой кривой должен следовать объект, чтобы спуститься под действием силы тяжести в ту же точку за тот же интервал времени, независимо от начальной точки; так называемой кривая таутохрона. Сложным методом, который был ранним использованием исчисление, он показал, что эта кривая циклоида, а не дугу окружности маятника,[48] подтверждая, что маятник не был изохронным, а наблюдение изохронности Галилеем было точным только для небольших колебаний.[49] Гюйгенс также решил проблему вычисления периода маятника произвольной формы (называемого составной маятник), открывая центр колебаний, и его взаимозаменяемость с точкой поворота.[50]
Существующий часовой механизм, краевой спуск, заставил маятники раскачиваться очень широкими дугами около 100 °.[51] Гюйгенс показал, что это является источником неточности, из-за чего период изменяется с изменениями амплитуды, вызванными небольшими неизбежными изменениями движущей силы часов.[52] Чтобы сделать его период изохронным, Гюйгенс установил циклоидальные металлические «отбивные» рядом с осями в своих часах, которые стесняли подвесной шнур и заставляли маятник следовать по циклоидной дуге (см. циклоидальный маятник).[53] Это решение оказалось не таким практичным, как простое ограничение качания маятника небольшими углами в несколько градусов. Осознание того, что только маленькие качели изохронный мотивировал развитие анкерный спуск около 1670 г., что уменьшило качание маятника на часах до 4–6 °.[51][54]
1721: Маятники с температурной компенсацией.

В 18-19 веках маятниковые часыроль самого точного хронометриста послужила стимулом для проведения множества практических исследований по улучшению маятников. Было обнаружено, что основной причиной ошибок было то, что стержень маятника расширялся и сжимался при изменении температуры окружающей среды, изменяя период качания.[8][55] Это было решено с изобретением маятников с температурной компенсацией, ртутного маятника в 1721 году.[56] и маятник сетки в 1726 году, уменьшив погрешность точных маятниковых часов до нескольких секунд в неделю.[53]
Точность измерений силы тяжести с помощью маятников ограничивалась трудностью определения местоположения их центр колебаний. В 1673 году Гюйгенс обнаружил, что маятник имеет тот же период, когда он подвешен к центру колебаний, как и когда он подвешен на оси.[17] а расстояние между двумя точками было равно длине простого гравитационного маятника того же периода.[14] В 1818 году британский капитан Генри Катер изобрел обратимый Маятник Катера[57] который использовал этот принцип, делая возможным очень точные измерения силы тяжести. В течение следующего столетия обратимый маятник был стандартным методом измерения абсолютного ускорения свободного падения.
1851: маятник Фуко
В 1851 г. Жан Бернар Леон Фуко показал, что плоскость колебания маятника, как и гироскоп, имеет тенденцию оставаться постоянным независимо от движения оси, и это может быть использовано для демонстрации вращение Земли. Он подвесил маятник, свободно качающийся в двух измерениях (позже названный Маятник Фуко) с купола Пантеон в Париже. Длина шнура составляла 67 м (220 футов). После того, как маятник был приведен в движение, наблюдалось, что плоскость качания прецессия или поверните на 360 ° по часовой стрелке примерно за 32 часа.[58]Это была первая демонстрация вращения Земли, которая не зависела от небесных наблюдений,[59] и началась "маятниковая мания", поскольку маятники Фуко были выставлены во многих городах и привлекали большие толпы.[60][61]
1930: сокращение использования
Около 1900 г.тепловое расширение материалы стали использоваться для стержней маятника в часах высочайшей точности и других инструментах. инвар, никелевый сплав стали, а позже плавленый кварц, что сделало компенсацию температуры тривиальной.[62] Прецизионные маятники были размещены в резервуарах низкого давления, в которых давление воздуха поддерживалось постоянным, чтобы предотвратить изменения периода из-за изменений плавучесть маятника из-за изменения атмосферное давление.[62] Лучшие маятниковые часы показывают точность около секунды в год.[63][64]
Точность отсчета времени маятника была превышена кварц кварцевый генератор, изобретенный в 1921 году, и кварцевые часы, изобретенные в 1927 году, заменили маятниковые часы как лучшие в мире хронометры.[2] Маятниковые часы использовались в качестве эталонов времени до Второй мировой войны, хотя французская служба времени продолжала использовать их в своем официальном эталонном ансамбле до 1954 года.[65] Маятник гравиметры были заменены гравиметрами "свободного падения" в 1950-х годах,[66] но маятниковые инструменты продолжали использоваться и в 1970-е годы.
Используйте для измерения времени

За 300 лет, с момента его открытия около 1582 года до разработки кварцевые часы в 1930-х годах маятник был мировым стандартом для точного хронометража.[2][67] Помимо часовых маятников, свободное качание секундные маятники широко использовались в качестве точных таймеров в научных экспериментах 17-18 веков. Маятники требуют большой механической устойчивости: изменение длины всего на 0,02%, 0,2 мм в маятнике напольных часов, вызовет ошибку в минуту в неделю.[68]
Маятники часов
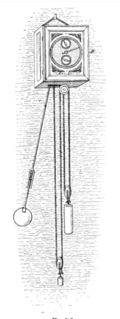
Маятники в часах (см. Пример справа) обычно состоят из гири или боб (б) подвешивается на стержень из дерева или металла (а).[8][69] Уменьшить сопротивление воздуха (на который приходится большая часть потерь энергии в точных часах)[70] Боб традиционно представляет собой гладкий диск с линзообразным поперечным сечением, хотя в старинных часах он часто имел резьбу или украшения, характерные для данного типа часов. В качественных часах боб делается настолько тяжелым, насколько может выдерживать подвеска и движение механизма, поскольку это улучшает регулировку часов (см. Точность ниже). Общий вес для секундный маятник бобы составляет 15 фунтов (6,8 кг).[71] Вместо того, чтобы висеть на вращаться, маятники часов обычно поддерживаются короткой прямой весна (г) гибкой металлической ленты. Это позволяет избежать трения и «люфта», вызванного шарниром, а небольшая сила изгиба пружины просто увеличивает силу маятника. восстанавливающая сила. Часы высочайшей точности имеют шарниры «ножевых» лезвий, опирающихся на агатовые пластины. Импульсы, заставляющие маятник качаться, создаются рукой, подвешенной за маятником, которая называется костыль, (е), который заканчивается на вилка, (е) зубцы которого охватывают стержень маятника. Костыль движется вперед и назад часами спусковой механизм, (г, ч).
Каждый раз, когда маятник перемещается в центральное положение, он освобождает один зубец аварийное колесо (грамм). Сила часов пружина или ведущий груз, свисающий со шкива, передаваемый через часы зубчатая передача, заставляет колесо вращаться, и зуб упирается в один из поддонов (час), коротко толкнув маятник. Колеса часов, привязанные к спусковому колесу, перемещаются вперед на фиксированную величину при каждом качании маятника, перемещая стрелки часов с постоянной скоростью.
Маятник всегда имеет средства регулировки периода, обычно с помощью регулировочной гайки. (c) под боб, который перемещает его вверх или вниз на удилище.[8][72] Перемещение боба вверх уменьшает длину маятника, заставляя маятник качаться быстрее, а часы выигрывают время. Некоторые прецизионные часы имеют небольшой вспомогательный юстировочный груз на валу с резьбой на бобе для более точной регулировки. Немного башенные часы а в точных часах используется лоток, прикрепленный к середине стержня маятника, на который можно добавлять или снимать небольшие грузы. Это эффективно смещает центр колебаний и позволяет регулировать скорость без остановки часов.[73][74]
Маятник необходимо подвешивать к жесткой опоре.[8][75] Во время работы любая эластичность допускает крошечные незаметные покачивания опоры, которые нарушают период часов, что приводит к ошибке. Часы с маятником должны быть надежно прикреплены к прочной стене.
Самая распространенная длина маятника в качественных часах, которая всегда используется в дедушкины часы, это секундный маятникдлиной около 1 метра (39 дюймов). В каминные часы, используются полусекундные маятники длиной 25 см (9,8 дюйма) или короче. Только несколько больших башенные часы используйте более длинные маятники, 1,5-секундный маятник длиной 2,25 м (7,4 фута) или иногда двухсекундный маятник длиной 4 м (13 футов) [8][76] который используется в Большой Бен.[77]
Температурная компенсация
Самым большим источником погрешности ранних маятников были небольшие изменения длины из-за теплового расширения и сжатия стержня маятника при изменении температуры окружающей среды.[78] Это было обнаружено, когда люди заметили, что маятниковые часы летом работают медленнее, на целых минуту в неделю.[55][79] (одним из первых был Годфрой Венделин, как сообщил Гюйгенс в 1658 г.).[80] Термическое расширение стержней маятника впервые было изучено Жан Пикар в 1669 г.[81][82] Маятник со стальным стержнем расширится примерно на 11,3 частей на миллион (ppm) при повышении температуры на каждый градус Цельсия, что приводит к потере около 0,27 секунды в день при повышении температуры на каждый градус Цельсия или 9 секунд в день при изменении температуры на 33 ° C (59 ° F). Деревянные стержни расширяются меньше, теряя всего около 6 секунд в день на изменение температуры на 33 ° C (59 ° F), поэтому качественные часы часто имеют деревянные стержни маятника. Древесину пришлось покрыть лаком, чтобы внутрь не проникал водяной пар, потому что изменение влажности также сказывалось на длине.
Маятник Меркурий
Первым устройством для компенсации этой ошибки был ртутный маятник, изобретенный Джордж Грэм[56] в 1721 г.[8][79] Жидкий металл Меркурий увеличивается в объеме с температурой. В ртутном маятнике вес маятника (боб) представляет собой сосуд с ртутью. При повышении температуры стержень маятника удлиняется, но ртуть также расширяется, и уровень ее поверхности в емкости немного поднимается, перемещая ее. центр масс ближе к оси маятника. Используя правильную высоту ртути в контейнере, эти два эффекта нейтрализуются, оставляя центр масс маятника и его период неизменными с температурой. Его главный недостаток заключался в том, что при изменении температуры стержень быстро достигал новой температуры, но массе ртути могло потребоваться день или два, чтобы достичь новой температуры, что привело к изменению скорости в течение этого времени.[83] Для улучшения теплового размещения часто использовалось несколько тонких контейнеров, сделанных из металла. Маятники с ртутью были стандартом, используемым в часах с точным регулятором в 20 веке.[84]
Маятник Gridiron
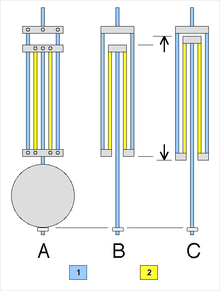
Наиболее распространенным компенсированным маятником был маятник. маятник сетки, изобретенный в 1726 г. Джон Харрисон.[8][79][83] Он состоит из чередующихся стержней из двух разных металлов, один с меньшим тепловым расширением (CTE), стали, и один с более высоким тепловым расширением, цинк или же латунь. Стержни соединены рамой, как показано на рисунке справа, так что увеличение длины цинковых стержней толкает боб вверх, укорачивая маятник. При повышении температуры стальные стержни с низким коэффициентом расширения удлиняют маятник, а цинковые стержни с высоким коэффициентом расширения - короче. При изготовлении стержней правильной длины большее расширение цинка нейтрализует расширение стальных стержней, которые имеют большую общую длину, и маятник остается той же длины с температурой.
Маятники с решетчатой решеткой из цинка и стали сделаны с 5 стержнями, но тепловое расширение латуни ближе к стали, поэтому для решетчатых решеток латунь-сталь обычно требуется 9 стержней. Маятники Gridiron приспосабливаются к изменениям температуры быстрее, чем ртутные маятники, но ученые обнаружили, что трение стержней, скользящих в их отверстиях в раме, заставляет маятники Gridiron настраиваться в серии крошечных прыжков.[83] В часах высокой точности из-за этого частота часов внезапно изменялась с каждым скачком. Позже выяснилось, что цинк подвержен слизняк. По этим причинам ртутные маятники использовались в часах высочайшей точности, а гридироны использовались в часах регулятора качества.
Маятники Gridiron стали настолько ассоциироваться с хорошим качеством, что и по сей день многие маятники обычных часов имеют декоративные «поддельные» решетки, которые фактически не имеют функции температурной компенсации.
Инвар и плавленый кварц
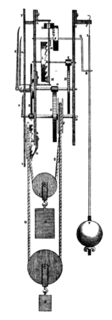
Примерно в 1900 году были разработаны материалы с низким тепловым расширением, которые можно было использовать в качестве маятниковых стержней, чтобы избавиться от необходимости в сложной температурной компенсации.[8][79] Они использовались только в нескольких часах высочайшей точности, прежде чем маятник стал устаревшим в качестве эталона времени. В 1896 г. Шарль Эдуард Гийом изобрел никель стали сплав Инвар. Это имеет CTE около 0,5 мкдюйма / (дюйм · ° F), что приводит к ошибкам маятниковой температуры свыше 71 ° F всего 1,3 секунды в день, и эту остаточную ошибку можно компенсировать до нуля с помощью нескольких сантиметров алюминия под маятниковым стержнем.[2][83] (это можно увидеть на изображении часов Riefler выше). Маятники из инвара были впервые применены в 1898 г. Часы-регулятор Riefler[85] с точностью до 15 миллисекунд в день. Пружины подвески Элинвар были использованы для устранения колебаний температуры пружины восстанавливающая сила на маятнике. Потом плавленый кварц использовался с еще более низким КТР. Эти материалы - лучший выбор для современных маятников высокой точности.[86]
Атмосферное давление
Воздействие окружающего воздуха на движущийся маятник сложное и требует механика жидкости чтобы рассчитать точно, но для большинства целей его влияние на период можно объяснить тремя эффектами:[62][87]
- К Принцип архимеда эффективный масса из боб уменьшается за счет плавучести вытесняемого воздуха, в то время как масса (инерция) остается прежним, уменьшая ускорение маятника во время его качания и увеличивая период. Это зависит от давления воздуха и плотности маятника, но не от его формы.
- Маятник увлекает с собой некоторое количество воздуха, когда он раскачивается, и масса этого воздуха увеличивает инерцию маятника, снова уменьшая ускорение и увеличивая период. Это зависит как от его плотности, так и от формы.
- Вязкий сопротивление воздуха замедляет скорость маятника. Это незначительно влияет на период, но рассеивает энергию, уменьшая амплитуду. Это уменьшает маятник. Добротность, требуя большей движущей силы от часового механизма для поддержания его движения, что вызывает повышенное нарушение периода.
Увеличение барометрическое давление немного увеличивают период маятника из-за первых двух эффектов примерно на 0,11 секунды в день на килопаскаль (0,37 секунды в день на килопаскаль). дюйм ртути или 0,015 секунды в день на торр).[62] Исследователи, использующие маятники для измерения ускорение свободного падения пришлось скорректировать период давления воздуха на высоте измерения, вычисляя эквивалентный период качания маятника в вакууме. Маятниковые часы были впервые использованы в резервуаре постоянного давления Фридрихом Тиде в 1865 г. Берлинская обсерватория,[88][89] и к 1900 году часы высочайшей точности были установлены в резервуарах, в которых поддерживалось постоянное давление, чтобы исключить изменения атмосферного давления. Как вариант, в некоторых небольших анероидный барометр Механизм, прикрепленный к маятнику, компенсировал этот эффект.
Сила тяжести
На маятники влияют изменения гравитационного ускорения, которое варьируется на целых 0,5% в разных местах на Земле, поэтому точные маятниковые часы необходимо откалибровать после перемещения. Даже перемещение маятниковых часов на вершину высокого здания может привести к потере измеримого времени из-за уменьшения силы тяжести.
Точность маятников как хронометристов
Элементы хронометража всех часов, в том числе маятники, балансирные колеса, то кристаллы кварца используется в кварцевые часы, и даже колеблющиеся атомы в атомные часы, в физике называются гармонические осцилляторы. Гармонические осцилляторы используются в часах потому, что они колеблются или колеблются с определенной частотой. резонансная частота или период и сопротивляться колебаниям с другими скоростями. Однако резонансная частота не может быть бесконечно «резкой». Вокруг резонансной частоты есть узкая естественная полоса частоты (или периоды), называемые ширина резонанса или же пропускная способность, где будет колебаться гармонический осциллятор.[90][91] В часах фактическая частота маятника может произвольно изменяться в пределах этой ширины резонанса в ответ на возмущения, но на частотах вне этого диапазона часы не будут работать вообще.
Q фактор

Мерой устойчивости гармонического осциллятора к возмущениям его периода колебаний является безразмерный параметр, называемый Q фактор равной резонансной частоте, деленной на ширина резонанса.[91][92] Чем выше Q, чем меньше ширина резонанса и тем более постоянна частота или период осциллятора для данного возмущения.[93] Величина, обратная Q, примерно пропорциональна предельной точности, достигаемой гармоническим осциллятором как эталоном времени.[94]
В Q связано с тем, как долго колебания осциллятора затухают. В Q маятника можно измерить, подсчитав количество колебаний, которое требуется для того, чтобы амплитуда качания маятника снизилась до 1 /е = 36,8% от его начального размаха и умножение на 2π.
В часах маятник должен получать толчки от часового механизма. движение чтобы он оставался в движении, чтобы восполнить энергию, которую маятник теряет на трение. Эти толчки, прикладываемые механизмом, называемым спусковой механизм, являются основным источником помех движению маятника. В Q равно 2π умноженное на энергию, запасенную в маятнике, деленную на энергию, потерянную на трение в течение каждого периода колебаний, что равно энергии, добавляемой спусковым механизмом каждый период. Можно видеть, что чем меньше доля энергии маятника, которая теряется на трение, тем меньше энергии необходимо добавить, чем меньше возмущение от спускового механизма, тем более `` независимым '' маятник от часового механизма и более постоянен его период. В Q маятника определяется выражением:
куда M масса боба, ω = 2π/Т - радианная частота колебаний маятника, а Γ это трение демпфирующая сила на маятник на единицу скорости.
ω фиксируется периодом маятника, а M ограничивается грузоподъемностью и жесткостью подвески. Итак Q часовых маятников увеличивается за счет минимизации потерь на трение (Γ). Прецизионные маятники подвешены на шарнирах с низким коэффициентом трения, состоящих из «ножевых» краев треугольной формы, опирающихся на агатовые пластины. Около 99% потерь энергии в свободно раскачивающемся маятнике происходит из-за трения воздуха, поэтому установка маятника в вакуумном резервуаре может увеличить Q, а значит, и точность в 100 раз.[95]
В Q Количество маятников колеблется от нескольких тысяч в обычных часах до нескольких сотен тысяч для маятников прецизионных регуляторов, качающихся в вакууме.[96] Качественные домашние маятниковые часы могут иметь Q 10 000 и точность 10 секунд в месяц. Наиболее точными серийно выпускаемыми маятниковыми часами были Свободные маятниковые часы Shortt-Synchronome, изобретенный в 1921 году.[2][63][97][98][99] Его Инвар маятник, раскачивающийся в вакуумном резервуаре, имел Q из 110 000[96] и частота ошибок около секунды в год.[63]
Их оценка 103–105 это одна из причин, почему маятники более точные хронометры, чем балансирные колеса в часах, с Q около 100–300, но менее точен, чем кристаллы кварца в кварцевые часы, с Q из 105–106.[2][96]
Спусковой механизм
Маятники (в отличие, например, от кристаллов кварца) имеют достаточно низкую Q что помехи, вызываемые импульсами, заставляющими их двигаться, обычно являются ограничивающим фактором их точности хронометража. Таким образом, дизайн спусковой механизм, механизм, который выдает эти импульсы, имеет большое влияние на точность часового маятника. Если бы импульсы, подаваемые на маятник спусковым механизмом, каждое качание могло быть в точности идентичным, реакция маятника была бы одинаковой, а его период был бы постоянным. Однако это недостижимо; Неизбежные случайные колебания силы из-за трения поддонов часов, изменения смазки и изменения крутящего момента, создаваемого источником питания часов, когда он работает, означают, что сила импульса, прикладываемого спусковым механизмом, изменяется.
Если эти изменения силы спуска вызывают изменения ширины качания маятника (амплитуды), это вызовет соответствующие незначительные изменения периода, поскольку (как обсуждалось вверху) маятник с конечным ходом не совсем изохронен. Следовательно, цель традиционной конструкции спуска - приложить усилие с надлежащим профилем и в правильной точке цикла маятника, чтобы изменения силы не влияли на амплитуду маятника. Это называется изохронный спуск.
Состояние Эйри
Часовщики на протяжении веков знали, что мешающее влияние движущей силы спускового механизма на период маятника минимально, если оно дается в виде короткого импульса, когда маятник проходит через его дно. положение равновесия.[2] Если импульс возникает до того, как маятник достигнет дна, во время нисходящего колебания, это приведет к сокращению естественного периода маятника, поэтому увеличение движущей силы уменьшит период. If the impulse occurs after the pendulum reaches bottom, during the upswing, it will lengthen the period, so an increase in drive force will increase the pendulum's period. В 1826 г. британский астроном Джордж Эйри доказал это; specifically, he proved that if a pendulum is driven by an impulse that is симметричный about its bottom equilibrium position, the pendulum's period will be unaffected by changes in the drive force.[100] The most accurate escapements, such as the бездельник, approximately satisfy this condition.[101]
Gravity measurement
Наличие ускорение свободного падения грамм in the periodicity equation (1) for a pendulum means that the local gravitational acceleration of the Earth can be calculated from the period of a pendulum. A pendulum can therefore be used as a gravimeter to measure the local сила тяжести, which varies by over 0.5% across the surface of the Earth.[102][Заметка 2] The pendulum in a clock is disturbed by the pushes it receives from the clock movement, so freeswinging pendulums were used, and were the standard instruments of гравиметрия up to the 1930s.
The difference between clock pendulums and gravimeter pendulums is that to measure gravity, the pendulum's length as well as its period has to be measured. The period of freeswinging pendulums could be found to great precision by comparing their swing with a precision clock that had been adjusted to keep correct time by the passage of stars overhead. In the early measurements, a weight on a cord was suspended in front of the clock pendulum, and its length adjusted until the two pendulums swung in exact synchronism. Then the length of the cord was measured. From the length and the period, грамм could be calculated from equation (1).
The seconds pendulum
В секундный маятник, a pendulum with a period of two seconds so each swing takes one second, was widely used to measure gravity, because its period could be easily measured by comparing it to precision regulator clocks, which all had seconds pendulums. By the late 17th century, the length of the seconds pendulum became the standard measure of the strength of gravitational acceleration at a location. By 1700 its length had been measured with submillimeter accuracy at several cities in Europe. For a seconds pendulum, грамм is proportional to its length:
Ранние наблюдения
- 1620: British scientist Френсис Бэкон was one of the first to propose using a pendulum to measure gravity, suggesting taking one up a mountain to see if gravity varies with altitude.[103]
- 1644: Even before the pendulum clock, French priest Марин Мерсенн first determined the length of the seconds pendulum was 39.1 inches (990 mm), by comparing the swing of a pendulum to the time it took a weight to fall a measured distance.
- 1669: Жан Пикар determined the length of the seconds pendulum at Paris, using a 1-inch (25 mm) copper ball suspended by an aloe fiber, obtaining 39.09 inches (993 mm).[104]
- 1672: The first observation that gravity varied at different points on Earth was made in 1672 by Jean Richer, who took a маятниковые часы к Cayenne, Французская Гвиана and found that it lost 2 1⁄2 minutes per day; its seconds pendulum had to be shortened by 1 1⁄4 lignes (2.6 mm) shorter than at Paris, to keep correct time.[105][106] In 1687 Исаак Ньютон в Principia Mathematica showed this was because the Earth had a slightly сплюснутый shape (flattened at the poles) caused by the центробежная сила of its rotation. At higher latitudes the surface was closer to the center of the Earth, so gravity increased with latitude.[106] From this time on, pendulums began to be taken to distant lands to measure gravity, and tables were compiled of the length of the seconds pendulum at different locations on Earth. В 1743 г. Алексис Клод Клеро created the first hydrostatic model of the Earth, Теорема Клеро,[104] which allowed the эллиптичность of the Earth to be calculated from gravity measurements. Progressively more accurate models of the shape of the Earth followed.
- 1687: Newton experimented with pendulums (described in Начала) and found that equal length pendulums with bobs made of different materials had the same period, proving that the gravitational force on different substances was exactly proportional to their масса (inertia).
- 1737: French mathematician Пьер Бугер made a sophisticated series of pendulum observations in the Анды mountains, Peru.[107] He used a copper pendulum bob in the shape of a double pointed cone suspended by a thread; the bob could be reversed to eliminate the effects of nonuniform density. He calculated the length to the center of oscillation of thread and bob combined, instead of using the center of the bob. He corrected for thermal expansion of the measuring rod and barometric pressure, giving his results for a pendulum swinging in vacuum. Bouguer swung the same pendulum at three different elevations, from sea level to the top of the high Peruvian Альтиплано. Gravity should fall with the inverse square of the distance from the center of the Earth. Bouguer found that it fell off slower, and correctly attributed the 'extra' gravity to the gravitational field of the huge Peruvian plateau. From the density of rock samples he calculated an estimate of the effect of the Альтиплано on the pendulum, and comparing this with the gravity of the Earth was able to make the first rough estimate of the density of the Earth.
- 1747: Даниэль Бернулли showed how to correct for the lengthening of the period due to a finite angle of swing θ0 by using the first order correction θ02/16, giving the period of a pendulum with an extremely small swing.[107]
- 1792: To define a pendulum standard of length for use with the new метрическая система, in 1792 Жан-Шарль де Борда и Жан-Доминик Кассини made a precise measurement of the seconds pendulum at Paris. They used a 1 1⁄2-inch (14 mm)[требуется разъяснение] platinum ball suspended by a 12-foot (3.7 m) iron wire. Their main innovation was a technique called the "method of coincidences" which allowed the period of pendulums to be compared with great precision. (Bouguer had also used this method). The time interval Δт between the recurring instants when the two pendulums swung in synchronism was timed. From this the difference between the periods of the pendulums, Т1 и Т2, could be calculated:
- 1821: Francesco Carlini made pendulum observations on top of Mount Cenis, Italy, from which, using methods similar to Bouguer's, he calculated the density of the Earth.[108] He compared his measurements to an estimate of the gravity at his location assuming the mountain wasn't there, calculated from previous nearby pendulum measurements at sea level. His measurements showed 'excess' gravity, which he allocated to the effect of the mountain. Modeling the mountain as a segment of a sphere 11 miles (18 km) in diameter and 1 mile (1.6 km) high, from rock samples he calculated its gravitational field, and estimated the density of the Earth at 4.39 times that of water. Later recalculations by others gave values of 4.77 and 4.95, illustrating the uncertainties in these geographical methods.
Kater's pendulum
The precision of the early gravity measurements above was limited by the difficulty of measuring the length of the pendulum, L . L was the length of an idealized simple gravity pendulum (described at top), which has all its mass concentrated in a point at the end of the cord. In 1673 Huygens had shown that the period of a rigid bar pendulum (called a compound pendulum) was equal to the period of a simple pendulum with a length equal to the distance between the вращаться point and a point called the center of oscillation, located under the центр гравитации, that depends on the mass distribution along the pendulum. But there was no accurate way of determining the center of oscillation in a real pendulum.
To get around this problem, the early researchers above approximated an ideal simple pendulum as closely as possible by using a metal sphere suspended by a light wire or cord. If the wire was light enough, the center of oscillation was close to the center of gravity of the ball, at its geometric center. This "ball and wire" type of pendulum wasn't very accurate, because it didn't swing as a rigid body, and the elasticity of the wire caused its length to change slightly as the pendulum swung.
However Huygens had also proved that in any pendulum, the pivot point and the center of oscillation were interchangeable.[17] That is, if a pendulum were turned upside down and hung from its center of oscillation, it would have the same period as it did in the previous position, and the old pivot point would be the new center of oscillation.
British physicist and army captain Генри Катер in 1817 realized that Huygens' principle could be used to find the length of a simple pendulum with the same period as a real pendulum.[57] If a pendulum was built with a second adjustable pivot point near the bottom so it could be hung upside down, and the second pivot was adjusted until the periods when hung from both pivots were the same, the second pivot would be at the center of oscillation, and the distance between the two pivots would be the length L of a simple pendulum with the same period.
Kater built a reversible pendulum (shown at right) consisting of a brass bar with two opposing pivots made of short triangular "knife" blades (а) near either end. It could be swung from either pivot, with the knife blades supported on agate plates. Rather than make one pivot adjustable, he attached the pivots a meter apart and instead adjusted the periods with a moveable weight on the pendulum rod (b,c). In operation, the pendulum is hung in front of a precision clock, and the period timed, then turned upside down and the period timed again. The weight is adjusted with the adjustment screw until the periods are equal. Then putting this period and the distance between the pivots into equation (1) gives the gravitational acceleration грамм very accurately.
Kater timed the swing of his pendulum using the "method of coincidences" and measured the distance between the two pivots with a micrometer. After applying corrections for the finite amplitude of swing, the buoyancy of the bob, the barometric pressure and altitude, and temperature, he obtained a value of 39.13929 inches for the seconds pendulum at London, in vacuum, at sea level, at 62 °F. The largest variation from the mean of his 12 observations was 0.00028 in.[109] representing a precision of gravity measurement of 7×10−6 (7 мГал or 70 µm/s2). Kater's measurement was used as Britain's official standard of length (see ниже) from 1824 to 1855.
Reversible pendulums (known technically as "convertible" pendulums) employing Kater's principle were used for absolute gravity measurements into the 1930s.
Later pendulum gravimeters
The increased accuracy made possible by Kater's pendulum helped make гравиметрия a standard part of геодезия. Since the exact location (latitude and longitude) of the 'station' where the gravity measurement was made was necessary, gravity measurements became part of геодезия, and pendulums were taken on the great geodetic surveys of the 18th century, particularly the Большой тригонометрический обзор Индии.
- Invariable pendulums: Kater introduced the idea of относительный gravity measurements, to supplement the абсолютный measurements made by a Kater's pendulum.[110] Comparing the gravity at two different points was an easier process than measuring it absolutely by the Kater method. All that was necessary was to time the period of an ordinary (single pivot) pendulum at the first point, then transport the pendulum to the other point and time its period there. Since the pendulum's length was constant, from (1) the ratio of the gravitational accelerations was equal to the inverse of the ratio of the periods squared, and no precision length measurements were necessary. So once the gravity had been measured absolutely at some central station, by the Kater or other accurate method, the gravity at other points could be found by swinging pendulums at the central station and then taking them to the other location and timing their swing there. Kater made up a set of "invariable" pendulums, with only one knife edge pivot, which were taken to many countries after first being swung at a central station at Kew Observatory, ВЕЛИКОБРИТАНИЯ.
- Airy's coal pit experiments: Starting in 1826, using methods similar to Bouguer, British astronomer Джордж Эйри attempted to determine the density of the Earth by pendulum gravity measurements at the top and bottom of a coal mine.[111][112] The gravitational force below the surface of the Earth decreases rather than increasing with depth, because by Закон Гаусса the mass of the spherical shell of crust above the subsurface point does not contribute to the gravity. The 1826 experiment was aborted by the flooding of the mine, but in 1854 he conducted an improved experiment at the Harton coal mine, using seconds pendulums swinging on agate plates, timed by precision chronometers synchronized by an electrical circuit. He found the lower pendulum was slower by 2.24 seconds per day. This meant that the gravitational acceleration at the bottom of the mine, 1250 ft below the surface, was 1/14,000 less than it should have been from the inverse square law; that is the attraction of the spherical shell was 1/14,000 of the attraction of the Earth. From samples of surface rock he estimated the mass of the spherical shell of crust, and from this estimated that the density of the Earth was 6.565 times that of water. Von Sterneck attempted to repeat the experiment in 1882 but found inconsistent results.
- Repsold-Bessel pendulum: It was time-consuming and error-prone to repeatedly swing the Kater's pendulum and adjust the weights until the periods were equal. Фридрих Бессель showed in 1835 that this was unnecessary.[113] As long as the periods were close together, the gravity could be calculated from the two periods and the center of gravity of the pendulum.[114] So the reversible pendulum didn't need to be adjustable, it could just be a bar with two pivots. Bessel also showed that if the pendulum was made symmetrical in form about its center, but was weighted internally at one end, the errors due to air drag would cancel out. Further, another error due to the finite diameter of the knife edges could be made to cancel out if they were interchanged between measurements. Bessel didn't construct such a pendulum, but in 1864 Adolf Repsold, under contract by the Swiss Geodetic Commission made a pendulum along these lines. The Repsold pendulum was about 56 cm long and had a period of about 3⁄4 второй. It was used extensively by European geodetic agencies, and with the Kater pendulum in the Survey of India. Similar pendulums of this type were designed by Charles Pierce and C. Defforges.
- Von Sterneck and Mendenhall gravimeters: In 1887 Austro-Hungarian scientist Robert von Sterneck developed a small gravimeter pendulum mounted in a temperature-controlled vacuum tank to eliminate the effects of temperature and air pressure. It used a "half-second pendulum," having a period close to one second, about 25 cm long. The pendulum was nonreversible, so the instrument was used for relative gravity measurements, but their small size made them small and portable. The period of the pendulum was picked off by reflecting the image of an электрическая искра created by a precision chronometer off a mirror mounted at the top of the pendulum rod. The Von Sterneck instrument, and a similar instrument developed by Thomas C. Mendenhall of the US Coast and Geodetic Survey в 1890 г.,[115] were used extensively for surveys into the 1920s.
- The Mendenhall pendulum was actually a more accurate timekeeper than the highest precision clocks of the time, and as the 'world's best clock' it was used by Альберт А. Михельсон in his 1924 measurements of the скорость света на Mt. Уилсон, Калифорния.[115]
- Double pendulum gravimeters: Starting in 1875, the increasing accuracy of pendulum measurements revealed another source of error in existing instruments: the swing of the pendulum caused a slight swaying of the tripod stand used to support portable pendulums, introducing error. In 1875 Charles S Peirce calculated that measurements of the length of the seconds pendulum made with the Repsold instrument required a correction of 0.2 mm due to this error.[116] In 1880 C. Defforges used a Интерферометр Майкельсона to measure the sway of the stand dynamically, and interferometers were added to the standard Mendenhall apparatus to calculate sway corrections.[117] A method of preventing this error was first suggested in 1877 by Hervé Faye and advocated by Peirce, Cellérier and Furtwangler: mount two identical pendulums on the same support, swinging with the same amplitude, 180° out of phase. The opposite motion of the pendulums would cancel out any sideways forces on the support. The idea was opposed due to its complexity, but by the start of the 20th century the Von Sterneck device and other instruments were modified to swing multiple pendulums simultaneously.
- Gulf gravimeter: One of the last and most accurate pendulum gravimeters was the apparatus developed in 1929 by the Gulf Research and Development Co.[118][119] It used two pendulums made of плавленый кварц, each 10.7 inches (270 mm) in length with a period of 0.89 second, swinging on pyrex knife edge pivots, 180° out of phase. They were mounted in a permanently sealed temperature and humidity controlled vacuum chamber. Stray electrostatic charges on the quartz pendulums had to be discharged by exposing them to a radioactive salt before use. The period was detected by reflecting a light beam from a mirror at the top of the pendulum, recorded by a chart recorder and compared to a precision crystal oscillator calibrated against the WWV radio time signal. This instrument was accurate to within (0.3–0.5)×10−7 (30–50 microgals or 3–5 nm/s2).[118] It was used into the 1960s.
Relative pendulum gravimeters were superseded by the simpler LaCoste zero-length spring gravimeter, invented in 1934 by Lucien LaCoste.[115] Absolute (reversible) pendulum gravimeters were replaced in the 1950s by free fall gravimeters, in which a weight is allowed to fall in a vacuum tank and its acceleration is measured by an optical интерферометр.[66]
Standard of length
Поскольку ускорение свободного падения is constant at a given point on Earth, the period of a simple pendulum at a given location depends only on its length. Additionally, gravity varies only slightly at different locations. Almost from the pendulum's discovery until the early 19th century, this property led scientists to suggest using a pendulum of a given период как стандарт длины.
Until the 19th century, countries based their systems of length measurement on prototypes, metal bar primary standards, such as the standard площадка in Britain kept at the Houses of Parliament, and the standard toise in France, kept at Paris. These were vulnerable to damage or destruction over the years, and because of the difficulty of comparing prototypes, the same unit often had different lengths in distant towns, creating opportunities for fraud.[120] Вовремя Просвещение scientists argued for a length standard that was based on some property of nature that could be determined by measurement, creating an indestructible, universal standard. The period of pendulums could be measured very precisely by timing them with clocks that were set by the stars. A pendulum standard amounted to defining the unit of length by the gravitational force of the Earth, for all intents constant, and the second, which was defined by the rotation rate of the Earth, also constant. The idea was that anyone, anywhere on Earth, could recreate the standard by constructing a pendulum that swung with the defined period and measuring its length.
Virtually all proposals were based on the секундный маятник, in which each swing (a half период) takes one second, which is about a meter (39 inches) long, because by the late 17th century it had become a standard for measuring gravity (see previous section). By the 18th century its length had been measured with sub-millimeter accuracy at a number of cities in Europe and around the world.
The initial attraction of the pendulum length standard was that it was believed (by early scientists such as Huygens and Wren) that gravity was constant over the Earth's surface, so a given pendulum had the same period at any point on Earth.[120] So the length of the standard pendulum could be measured at any location, and would not be tied to any given nation or region; it would be a truly democratic, worldwide standard. Although Richer found in 1672 that gravity varies at different points on the globe, the idea of a pendulum length standard remained popular, because it was found that gravity only varies with широта. Gravitational acceleration increases smoothly from the экватор к полюса, из-за сплюснутый shape of the Earth, so at any given latitude (east–west line), gravity was constant enough that the length of a seconds pendulum was the same within the measurement capability of the 18th century. Thus the unit of length could be defined at a given latitude and measured at any point along that latitude. For example, a pendulum standard defined at 45° north latitude, a popular choice, could be measured in parts of France, Italy, Croatia, Serbia, Romania, Russia, Kazakhstan, China, Mongolia, the United States and Canada. In addition, it could be recreated at any location at which the gravitational acceleration had been accurately measured.
By the mid 19th century, increasingly accurate pendulum measurements by Эдвард Сабин и Томас Янг revealed that gravity, and thus the length of any pendulum standard, varied measurably with local geologic features such as mountains and dense subsurface rocks.[121] So a pendulum length standard had to be defined at a single point on Earth and could only be measured there. This took much of the appeal from the concept, and efforts to adopt pendulum standards were abandoned.
Ранние предложения
One of the first to suggest defining length with a pendulum was Flemish scientist Исаак Бекман[122] who in 1631 recommended making the seconds pendulum "the invariable measure for all people at all times in all places".[123] Марин Мерсенн, who first measured the seconds pendulum in 1644, also suggested it. The first official proposal for a pendulum standard was made by the British Королевское общество in 1660, advocated by Кристиан Гюйгенс и Оле Рёмер, basing it on Mersenne's work,[124] and Huygens in Часы Oscillatorium proposed a "horary foot" defined as 1/3 of the seconds pendulum. Кристофер Рен was another early supporter. The idea of a pendulum standard of length must have been familiar to people as early as 1663, because Сэмюэл Батлер satirizes it in Худибрас:[125]
- Upon the bench I will so handle ‘em
- That the vibration of this pendulum
- Shall make all taylors’ yards of one
- Единодушное мнение
In 1671 Жан Пикар proposed a pendulum-defined 'universal foot' in his influential Mesure de la Terre.[126] Gabriel Mouton around 1670 suggested defining the toise either by a seconds pendulum or a minute of terrestrial degree. A plan for a complete system of units based on the pendulum was advanced in 1675 by Italian polymath Tito Livio Burratini. In France in 1747, geographer Шарль Мари де ла Кондамин proposed defining length by a seconds pendulum at the equator; since at this location a pendulum's swing wouldn't be distorted by the Earth's rotation. Джеймс Стюарт (1780) and Джордж Скин Кейт were also supporters.
By the end of the 18th century, when many nations were reforming their weight and measure systems, то секундный маятник was the leading choice for a new definition of length, advocated by prominent scientists in several major nations. In 1790, then US Secretary of State Томас Джеферсон proposed to Congress a comprehensive decimalized US 'metric system' based on the seconds pendulum at 38° North latitude, the mean latitude of the United States.[127] Никаких действий по этому предложению принято не было. In Britain the leading advocate of the pendulum was politician John Riggs Miller.[128] When his efforts to promote a joint British–French–American metric system fell through in 1790, he proposed a British system based on the length of the seconds pendulum at London. This standard was adopted in 1824 (below).
Метр
In the discussions leading up to the French adoption of the метрическая система in 1791, the leading candidate for the definition of the new unit of length, the метр, was the seconds pendulum at 45° North latitude. It was advocated by a group led by French politician Талейран и математик Antoine Nicolas Caritat de Condorcet. This was one of the three final options considered by the Французская Академия Наук комитет. However, on March 19, 1791 the committee instead chose to base the metre on the length of the меридиан through Paris. A pendulum definition was rejected because of its variability at different locations, and because it defined length by a unit of time. (However, since 1983 the metre has been officially defined in terms of the length of the second and the speed of light.) A possible additional reason is that the radical French Academy didn't want to base their new system on the second, a traditional and nondecimal unit from the старый режим.
Although not defined by the pendulum, the final length chosen for the metre, 10−7 of the pole-to-equator дуга меридиана, was very close to the length of the seconds pendulum (0.9937 m), within 0.63%. Although no reason for this particular choice was given at the time, it was probably to facilitate the use of the seconds pendulum as a secondary standard, as was proposed in the official document. So the modern world's standard unit of length is certainly closely linked historically with the seconds pendulum.
Britain and Denmark
Britain and Denmark appear to be the only nations that (for a short time) based their units of length on the pendulum. In 1821 the Danish inch was defined as 1/38 of the length of the mean solar seconds pendulum at 45° latitude at the meridian of Скаген, at sea level, in vacuum.[129][130] The British parliament passed the Imperial Weights and Measures Act in 1824, a reform of the British standard system which declared that if the prototype standard площадка was destroyed, it would be recovered by defining the дюйм so that the length of the solar seconds pendulum at London, at уровень моря, in a vacuum, at 62 °F was 39.1393 inches.[131] This also became the US standard, since at the time the US used British measures. However, when the prototype yard was lost in the 1834 Houses of Parliament fire, it proved impossible to recreate it accurately from the pendulum definition, and in 1855 Britain repealed the pendulum standard and returned to prototype standards.
Другое использование
Seismometers
A pendulum in which the rod is not vertical but almost horizontal was used in early сейсмометры for measuring earth tremors. The bob of the pendulum does not move when its mounting does, and the difference in the movements is recorded on a drum chart.
Schuler tuning
As first explained by Maximilian Schuler in a 1923 paper, a pendulum whose period exactly equals the orbital period of a hypothetical satellite orbiting just above the surface of the earth (about 84 minutes) will tend to remain pointing at the center of the earth when its support is suddenly displaced. This principle, called Schuler tuning, используется в инерциальные системы наведения in ships and aircraft that operate on the surface of the Earth. No physical pendulum is used, but the control system that keeps the inertial platform содержащий гироскопы stable is modified so the device acts as though it is attached to such a pendulum, keeping the platform always facing down as the vehicle moves on the curved surface of the Earth.
Coupled pendulums
In 1665 Huygens made a curious observation about pendulum clocks. Two clocks had been placed on his накидка, and he noted that they had acquired an opposing motion. That is, their pendulums were beating in unison but in the opposite direction; 180° не в фазе. Regardless of how the two clocks were started, he found that they would eventually return to this state, thus making the first recorded observation of a coupled oscillator.[132]
The cause of this behavior was that the two pendulums were affecting each other through slight motions of the supporting mantlepiece. Этот процесс называется увлечение или же mode locking in physics and is observed in other coupled oscillators. Synchronized pendulums have been used in clocks and were widely used in gravimeters в начале 20 века. Although Huygens only observed out-of-phase synchronization, recent investigations have shown the existence of in-phase synchronization, as well as "death" states wherein one or both clocks stops.[133][134]
Религиозная практика
Pendulum motion appears in religious ceremonies as well. The swinging ладан burner called a курильница, также известный как кадило, is an example of a pendulum.[135] Pendulums are also seen at many gatherings in eastern Mexico where they mark the turning of the tides on the day which the tides are at their highest point. Смотрите также pendulums for divination and dowsing.
Образование
Pendulums are widely used in science education as an example of a гармонический осциллятор, to teach динамика и oscillatory motion. One use is to demonstrate the law of conservation of energy.[136][137] A heavy object such as a шар для боулинга[138] или же шаровой таран[136] is attached to a string. The weight is then moved to within a few inches of a volunteer's face, then released and allowed to swing and come back. In most instances, the weight reverses direction and then returns to (almost) the same position as the original release location — т.е. a small distance from the volunteer's face — thus leaving the volunteer unharmed. On occasion the volunteer is injured if either the volunteer does not stand still[139] or the pendulum is initially released with a push (so that when it returns it surpasses the release position).
Устройство пыток
It is claimed that the pendulum was used as an instrument of пытка и исполнение посредством испанская инквизиция[140] в 18 веке. The allegation is contained in the 1826 book The history of the Inquisition of Spain by the Spanish priest, historian and либеральный активист Juan Antonio Llorente.[141] A swinging pendulum whose edge is a knife blade slowly descends toward a bound prisoner until it cuts into his body.[142] This method of torture came to popular consciousness through the 1842 short story "Яма и маятник" by American author Эдгар Аллан По[143] but there is considerable skepticism that it actually was used.
Most knowledgeable sources are skeptical that this torture was ever actually used.[144][145][146] The only evidence of its use is one paragraph in the preface to Llorente's 1826 История,[141] relating a second-hand account by a single prisoner released from the Inquisition's Madrid dungeon in 1820, who purportedly described the pendulum torture method. Modern sources point out that due to Jesus' admonition against bloodshed, Inquisitors were only allowed to use torture methods which did not spill blood, and the pendulum method would have violated this stricture. One theory is that Llorente misunderstood the account he heard; the prisoner was actually referring to another common Inquisition torture, the дыба (garrucha), in which the prisoner has his hands tied behind his back and is hoisted off the floor by a rope tied to his hands.[146] This method was also known as the "pendulum". Poe's popular horror tale, and public awareness of the Inquisition's other brutal methods, has kept the myth of this elaborate torture method alive.
Смотрите также
- Маятник Рэлея – Лоренца
- Barton's pendulums
- Маятник Блэкберна
- Conical pendulum
- Циклоидный маятник
- Doubochinski's pendulum
- Двойной маятник
- Двойной перевернутый маятник
- Маятник Фуко
- Маятник Furuta
- Gridiron pendulum
- Маятник инерционного колеса
- Перевернутый маятник
- Harmonograph (a.k.a. "Lissajous pendulum")
- Маятник капицы
- Kater's pendulum
- Метроном
- N-pendulum[147]
- Маятник (математика)
- Маятниковые часы
- Pendulum rocket fallacy
- Quantum pendulum
- Маятник секунд
- Простые гармонические колебания
- Spherical pendulum
- Spring pendulum
- Torsional pendulum
Примечания
The value of g reflected by the period of a pendulum varies from place to place. The gravitational force varies with distance from the center of the Earth, i.e. with altitude - or because the Earth's shape is oblate, g varies with latitude.A more important cause of this reduction in g at the equator is because the equator is spinning at one revolution per day, so the acceleration by the gravitational force is partially canceled there by the центробежная сила.
Рекомендации
Note: most of the sources below, including books, can be viewed online through the links given.
- ^ "Pendulum". Miriam Webster's Collegiate Encyclopedia. Miriam Webster. 2000. с. 1241. ISBN 978-0-87779-017-4.
- ^ а б c d е ж грамм Marrison, Warren (1948). "The Evolution of the Quartz Crystal Clock". Технический журнал Bell System. 27 (3): 510–588. Дои:10.1002/j.1538-7305.1948.tb01343.x. Архивировано из оригинал на 2011-07-17.
- ^ Morris, William, Ed. (1979). The American Heritage Dictionary, New College Ed. New York: Houghton-Mifflin. п.969. ISBN 978-0-395-20360-6.
- ^ defined by Christiaan Huygens: Huygens, Christian (1673). "Horologium Oscillatorium" (PDF). 17centurymaths. 17thcenturymaths.com. Получено 2009-03-01., Part 4, Definition 3, translated July 2007 by Ian Bruce
- ^ а б Nave, Carl R. (2006). "Simple pendulum". Hyperphysics. Georgia State Univ. Получено 2008-12-10.
- ^ Xue, Linwei (2007). "Pendulum Systems". Seeing and Touching Structural Concepts. Civil Engineering Dept., Univ. of Manchester, UK. Получено 2008-12-10.
- ^ Weisstein, Eric W. (2007). "Simple Pendulum". Eric Weisstein's world of science. Wolfram Research. Получено 2009-03-09.
- ^ а б c d е ж грамм час я Milham, Willis I. (1945). Время и хронометристы. Макмиллан., p.188-194
- ^ Холлидей, Дэвид; Robert Resnick; Jearl Walker (1997). Fundamentals of Physics, 5th Ed. Нью-Йорк: Джон Вили и сыновья. п.381. ISBN 978-0-471-14854-8.
- ^ Cooper, Herbert J. (2007). Научные инструменты. New York: Hutchinson's. п. 162. ISBN 978-1-4067-6879-4.
- ^ а б Нельсон, Роберт; M. G. Olsson (February 1987). "The pendulum – Rich physics from a simple system" (PDF). Американский журнал физики. 54 (2): 112–121. Bibcode:1986AmJPh..54..112N. Дои:10.1119/1.14703. Получено 2008-10-29.
- ^ "Clock". Британская энциклопедия, 11-е изд.. 6. The Encyclopædia Britannica Publishing Co. 1910. p. 538. Получено 2009-03-04. includes a derivation
- ^ Deschaine, J. S.; Suits, B. H. (2008). "The hanging cord with a real tip mass". Европейский журнал физики. 29 (6): 1211–1222. Bibcode:2008EJPh...29.1211D. Дои:10.1088/0143-0807/29/6/010.
- ^ а б Huygens, Christian (1673). "Horologium Oscillatorium". 17centurymaths. Translated by Bruce, Ian. 17thcenturymaths.com. Получено 2009-03-01., Part 4, Proposition 5
- ^ Глазго, Дэвид (1885). Часы и изготовление часов. Лондон: Cassel & Co., стр.278.
- ^ Fowles, Grant R (1986). Analytical Mechanics, 4th Ed. NY, NY: Saunders. pp. 202 ff.
- ^ а б c Huygens (1673) Horologium Oscillatorium, Part 4, Proposition 20
- ^ Morton, W. Scott and Charlton M. Lewis (2005). China: Its History and Culture. New York: McGraw-Hill, Inc., p. 70
- ^ а б Needham, Volume 3, 627-629
- ^ Good, Gregory (1998). Sciences of the Earth: An Encyclopedia of Events, People, and Phenomena. Рутледж. п. 394. ISBN 978-0-8153-0062-5.
- ^ "Маятник". Энциклопедия Американа. 21. The Americana Corp. 1967. p. 502. Получено 2009-02-20.
- ^ Baker, Cyril Clarence Thomas (1961). Dictionary of Mathematics. Г. Ньюнес. п. 176.
- ^ Newton, Roger G. (2004). Маятник Галилея: от ритма времени к созданию материи. US: Harvard University Press. п.52. ISBN 978-0-674-01331-5.
- ^ King, D. A. (1979). "Ibn Yunus and the pendulum: a history of errors". Archives Internationales d'Histoire des Sciences. 29 (104): 35–52.
- ^ Hall, Bert S. (September 1978). "The scholastic pendulum". Анналы науки. 35 (5): 441–462. Дои:10.1080/00033797800200371. ISSN 0003-3790.
- ^ O'Connor, J. J.; Robertson, E. F. (November 1999). "Abu'l-Hasan Ali ibn Abd al-Rahman ibn Yunus". Сент-Эндрюсский университет. Получено 2007-05-29.
- ^ Matthews, Michael R. (2000). Time for science education. Springer. п. 87. ISBN 978-0-306-45880-4.
- ^ а б Drake, Stillman (2003). Galileo at Work: His scientific biography. USA: Courier Dover. С. 20–21. ISBN 978-0-486-49542-2.
- ^ Галилей, Галилей (1890–1909; перепечатано в 1929–1939 и 1964–1966 годах). Фаваро, Антонио (ред.). Le Opere di Galileo Galilei, Edizione Nazionale [Произведения Галилео Галилея, Национальное издание] (на итальянском). Флоренция: Барбера. ISBN 978-88-09-20881-0. Проверить значения даты в:
| дата =(помощь) - ^ Мурдин, Пол (2008). Полный меридиан славы: опасные приключения в соревновании по измерению Земли. Springer. п. 41. ISBN 978-0-387-75533-5.
- ^ La Lampada di GalileoФранческо Малагуцци Валери, для Archivio storico dell'arte, Volume 6 (1893); Редактор Доменико Ньоли; Издательство Danesi, Рим; Стр. 215-218.
- ^ а б c Ван Хелден, Альберт (1995). «Маятниковые часы». Проект Галилео. Рис Univ. Получено 2009-02-25.
- ^ Дрейк 2003, с.419–420
- ^ хотя есть необоснованные ссылки на предыдущие маятниковые часы, сделанные другими: Ашер, Эбботт Пейсон (1988). История механических изобретений. Курьер Дувр. С. 310–311. ISBN 978-0-486-25593-4.
- ^ Эйдсон, Джон С. (2006). Измерение, управление и обмен данными с использованием IEEE 1588. Бурхаузен. п. 11. ISBN 978-1-84628-250-8.
- ^ Милхэм 1945, стр.145
- ^ а б О'Коннор, Дж. Дж .; Э.Ф. Робертсон (август 2002 г.). "Роберт Гук". Биографии, Архив истории математики MacTutor. Школа математики и статистики, Univ. Сент-Эндрюс, Шотландия. Получено 2009-02-21.
- ^ Науэнберг, Майкл (2006). «Важнейший вклад Роберта Гука в орбитальную динамику». Роберт Гук: исследования к 300-летию. Издательство Ashgate. С. 17–19. ISBN 0-7546-5365-X.
- ^ Науэнберг, Майкл (2004). "Гук и Ньютон: предсказание движения планет". Физика сегодня. 57 (2): 13. Bibcode:2004ФТ .... 57б..13Н. Дои:10.1063/1.1688052. Получено 2007-05-30.
- ^ Группа компаний KGM, Inc. (2004 г.). «Гелиоцентрические модели». Магистр наук. Архивировано из оригинал на 2007-07-13. Получено 2007-05-30.
- ^ Лензен, Виктор Ф .; Роберт П. Мултауф (1964). "Документ 44: Развитие гравитационных маятников в XIX веке". Бюллетень 240 Национального музея США: Вклад Историко-технологического музея, перепечатанный в Бюллетене Смитсоновского института. Вашингтон: Пресса Смитсоновского института. п. 307. Получено 2009-01-28.
- ^ Богаче, Жан (1679). Астрономические наблюдения и физические данные на острове Кайенн. Mémoires de l'Académie Royale des Sciences. Bibcode:1679oaep.book ..... R. цитируется в Ленцен и Мультауф, 1964 г., стр.307
- ^ Ленцен и Мультауф, 1964 г., стр.307
- ^ Пойнтинг, Джон Генри; Джозеф Джон Томпсон (1907). Учебник физики, 4-е изд.. Лондон: Charles Griffin & Co., стр.20–22.
- ^ Гюйгенс, Кристиан; перевод Яна Брюса (июль 2007 г.). "Часы Осцилляторий" (PDF). 17 век. 17thcenturymaths.com. Получено 2009-03-01.
- ^ Созвездие Часы позже был назван в честь этой книги.
- ^ Мэтьюз, Майкл Р. (1994). Преподавание естественных наук: роль истории и философии науки. Психология Press. С. 121–122. ISBN 978-0-415-90899-3.
- ^ Гюйгенс, Horologium Oscillatorium, Часть 2, Предложение 25
- ^ Махони, Майкл С. (19 марта 2007 г.). "Кристиан Гюйгенс: Измерение времени и долготы в море". Университет Принстона. Архивировано из оригинал 4 декабря 2007 г.. Получено 2007-05-27.
- ^ Бевилаква, Фабио; Лидия Фаломо; Лучио Фрегонезе; Энрико Джанетто; Франко Джудизе; Паоло Маскеретти (2005). «Маятник: от сдержанного падения к концепции потенциала». Маятник: научные, исторические, философские и образовательные перспективы. Springer. С. 195–200. ISBN 1-4020-3525-X. Получено 2008-02-26. дает подробное описание методов Гюйгенса
- ^ а б Хедрик, Майкл (2002). "Происхождение и эволюция спуска якорных часов". Журнал «Системы управления», Инст. Инженеров-электриков и электронщиков. 22 (2). Архивировано из оригинал 25 октября 2009 г.. Получено 2007-06-06.
- ^ "... на него влияет либо несдержанность воздуха, либо какие-либо неисправности в механизме, поэтому костыль QR не всегда приводится в действие одной и той же силой ... При больших дугах колебания занимают больше времени, как я объяснил, поэтому по этой причине существует некоторая неравномерность хода часов ...", Гюйгенс, Христиан (1658). Часы (PDF). Гаага: Адриан Влакк., перевод Эрнеста Л. Эдвардса (декабрь 1970 г.) Антикварные часы, Том 7, Номер 1
- ^ а б Эндрюс, W.J.H. Часы и часы: скачок к точности в Мейси, Сэмюэл (1994). Энциклопедия времени. Тейлор и Фрэнсис. С. 123–125. ISBN 978-0-8153-0615-3.
- ^ Ашер, 1988 г., стр.312
- ^ а б Беккет, Эдмунд (1874). Элементарный трактат о часах, часах и колоколах, 6-е изд.. Лондон: Lockwood & Co., стр. 50.
- ^ а б Грэм, Джордж (1726). «Устройство, позволяющее избежать отклонений в движении часов, вызванных воздействием тепла и холода на стержень маятника». Философские труды Королевского общества. 34 (392–398): 40–44. Дои:10.1098 / рстл.1726.0006. S2CID 186210095. цитируется в Дэй, Лэнс; Иэн Макнил (1996). Биографический словарь истории техники. Тейлор и Фрэнсис. п. 300. ISBN 978-0-415-06042-4.
- ^ а б Катер, Генри (1818). «Отчет об экспериментах по определению длины секунд колебания маятника на широте Лондона». Фил. Пер. Р. Соц. 104 (33): 109. Получено 2008-11-25.
- ^ Рубин, Джулиан (сентябрь 2007 г.). «Изобретение маятника Фуко». По пути открытий. Получено 2007-10-31.
- ^ Амир Акзель (2003) Леон Фуко: Его жизнь, времена и достижения в Мэтьюз, Майкл Р .; Колин Ф. Голд; Артур Стиннер (2005). Маятник: научные, исторические, образовательные и философские перспективы. Springer. п. 177. ISBN 978-1-4020-3525-8.
- ^ Джованнанджели, Франсуаза (ноябрь 1996 г.). "Крутящийся маятник Фуко на Пантеоне". Парижские страницы. Архивировано из оригинал на 2007-06-09. Получено 2007-05-25.
- ^ Тобин, Уильям (2003). Жизнь и наука Леона Фуко: человека, который доказал, что Земля вращается. Великобритания: Издательство Кембриджского университета. С. 148–149. ISBN 978-0-521-80855-2.
- ^ а б c d "Часы". Британская энциклопедия, 11-е изд.. 6. The Encyclopdia Britannica Publishing Co., 1910. С. 540–541.. Получено 2009-03-04.
- ^ а б c Джонс, Тони (2000). Разделение второго: история атомного времени. CRC Press. п. 30. ISBN 978-0-7503-0640-9.
- ^ Калер, Джеймс Б. (2002). Постоянно меняющееся небо: Путеводитель по небесной сфере. Великобритания: Cambridge Univ. Нажмите. п. 183. ISBN 978-0-521-49918-7.
- ^ Audoin, Клод; Бернар Гино; Стивен Лайл (2001). Измерение времени: время, частота и атомные часы. Великобритания: Cambridge Univ. Нажмите. п. 83. ISBN 978-0-521-00397-1.
- ^ а б Торге, Вольфганг (2001). Геодезия: Введение. Вальтер де Грюйтер. п. 177. ISBN 978-3-11-017072-6.
- ^ Милхэм 1945, стр.334
- ^ рассчитывается по уравнению (1)
- ^ Глазго, Дэвид (1885). Часы и изготовление часов. Лондон: Cassel & Co., стр.279–284.
- ^ Маттис, Роберт Дж. (2004). Точные часы с маятником. Великобритания: Oxford Univ. Нажмите. п. 4. ISBN 978-0-19-852971-2.
- ^ Mattheys, 2004, стр. 13
- ^ Мэттис 2004, с.91-92
- ^ Беккет 1874, стр.48
- ^ «Регулирование». Энциклопедия часов и часов. Рынок старых и проданных антиквариата. 2006 г.. Получено 2009-03-09.
- ^ Беккет 1874, стр.43
- ^ Глазго 1885, стр.282
- ^ "Факты о великих часах". Большой Бен. Лондон: Парламент Великобритании. 13 ноября 2009 г. Архивировано с оригинал 7 октября 2009 г.. Получено 31 октября 2012.
- ^ Мэттис 2004, стр.3
- ^ а б c d "Часы". Британская энциклопедия, 11-е изд.. 6. The Encyclopædia Britannica Publishing Co., 1910. С. 539–540.. Получено 2009-03-04.
- ^ Гюйгенс, Христиан (1658). Часы (PDF). Гаага: Адриан Влакк., перевод Эрнеста Л. Эдвардса (декабрь 1970 г.) Антикварные часы, Том 7, Номер 1
- ^ Зупко, Рональд Эдвард (1990). Революция в измерениях: меры веса и веса в Западной Европе со времен науки. Дайан Паблишинг. п. 131. ISBN 978-0-87169-186-6.
- ^ Пикард, Жан, La Mesure de la Terre [Измерение Земли] (Париж, Франция: Imprimerie Royale, 1671 г.), п. 4. Пикард описал маятник, состоящий из медного шара диаметром в дюйм, подвешенного на нити из жалость, волокно из растения алоэ. Затем Пикард упоминает, что температура слегка влияет на длину этого маятника: "Il est vray que cette longueur ne s'est pas toûjours Trouvees si précise, & qu'il a semblé qu'elle devoit estre toûjours un peu accourcie en Hyver, & allongée en esté; mais c'est seulement de la dixieme partie d 'une ligne… " (Верно, что эта длина [маятника] не всегда оказывается такой точной, и казалось, что ее всегда нужно немного сокращать зимой и удлинять летом; но это только на одну десятую часть строки [1 Ligne (линия) = 2,2558 мм]…)
- ^ а б c d Мэттис 2004, стр.7-12
- ^ Милхэм 1945, стр.335
- ^ Милхэм 1945, стр.331-332
- ^ Мэттис 2004, Часть 3, с.153-179
- ^ Пойнтинг и Томпсон, 1907, стр. 13-14.
- ^ Апдеграф, Милтон (7 февраля 1902 г.). «Об измерении времени». Наука. 15 (371): 218–219. Дои:10.1126 / science.ns-15.374.218-a. PMID 17793345. S2CID 21030470. Получено 2009-07-13.
- ^ Данвуди, Холзи (1917). Заметки, задачи и лабораторные упражнения по механике, звуку, свету, термомеханике и гидравлике, 1-е изд.. Нью-Йорк: Джон Вили и сыновья. п. 87.
- ^ «Ширина резонанса». Глоссарий. Отдел времени и частоты, Национальный институт стандартов и технологий США. 2009. Архивировано с оригинал на 2009-01-30. Получено 2009-02-21.
- ^ а б Джесперсен, Джеймс; Фитц-Рэндольф, Джейн; Робб, Джон (1999). От солнечных часов к атомным часам: понимание времени и частоты. Нью-Йорк: Курьер Дувр. С. 41–50. ISBN 978-0-486-40913-9. стр.39
- ^ Маттис, Роберт Дж. (2004). Точные часы с маятником. Великобритания: Oxford Univ. Нажмите. С. 27–36. ISBN 978-0-19-852971-2. есть отличное всестороннее обсуждение спора о применимости Q с точностью до маятников.
- ^ «Фактор качества, Q». Глоссарий. Отдел времени и частоты, Национальный институт стандартов и технологий США. 2009. Архивировано с оригинал на 2008-05-04. Получено 2009-02-21.
- ^ Matthys, 2004, стр.32, рис. 7.2 и текст
- ^ Маттис, 2004, стр.81.
- ^ а б c «Q, фактор качества». Часы и журнал часов. Сайт Orologeria Lamberlin. Получено 2009-02-21.
- ^ Милхэм 1945, стр.615
- ^ "Часы Райфлера и Шортта". Институт времени и технологий JagAir. Получено 2009-12-29.
- ^ Беттс, Джонатан (22 мая 2008 г.). «Заключение эксперта, дело 6 (2008-09), регулирующий орган Уильяма Гамильтона Шортта». Слушания по лицензированию экспорта, Комитет по надзору за экспортом произведений искусства и предметов, представляющих культурный интерес. Совет музеев, библиотек и архивов Великобритании. Архивировано из оригинал (DOC) 25 октября 2009 г.. Получено 2009-12-29.
- ^ Эйри, Джордж Биддл (26 ноября 1826 г.). «О возмущениях маятников и весов и теории эвакуации». Труды Кембриджского философского общества. 3 (Часть 1): 105. Получено 2008-04-25.
- ^ Беккет 1874, с.75-79
- ^ Вочадло, Лидунка. «Гравитация, форма Земли, изостазия, момент инерции». Получено 5 ноября 2012.
- ^ Бейкер, Лайман А. (весна 2000 г.). "Канцлер Бэкон". Английский 233 - Введение в западные гуманитарные науки. Департамент английского языка, Университет штата Канзас. Получено 2009-02-20.
- ^ а б Пойнтинг и Томпсон 1907, стр.9
- ^ Пойнтинг, Джон Генри; Джозеф Джон Томпсон (1907). Учебник физики, 4-е изд.. Лондон: Charles Griffin & Co., стр.20.
- ^ а б Виктор Ф., Лензен; Роберт П. Мултауф (1964). "Документ 44: Развитие гравитационных маятников в XIX веке". Бюллетень 240 Национального музея США: Вклад Историко-технологического музея, перепечатанный в Бюллетене Смитсоновского института. Вашингтон: Пресса Смитсоновского института. п. 307. Получено 2009-01-28.
- ^ а б Пойнтинг и Томпсон, 1907, стр.10.
- ^ Пойнтинг, Джон Генри (1894). Средняя плотность Земли. Лондон: Чарльз Гриффин. стр.22–24.
- ^ Кокс, Джон (1904). Механика. Кембридж, Великобритания: Cambridge Univ. Нажмите. стр.311–312.
- ^ Пойнтинг и Томсон 1904, стр.23.
- ^ Пойнтинг, Джон Генри (1894). Средняя плотность Земли. Лондон: Charles Griffin & Co., стр.24–29.
- ^ «Гравитация». Британская энциклопедия, 11-е изд.. 7. The Encyclopdia Britannica Co., 1910. стр. 386. Получено 2009-05-28.
- ^ Ленцен и Мультауф, 1964, стр. 320.
- ^ Пойнтинг и Томпсон 1907, стр.18
- ^ а б c «Взлеты и падения гравиметрических исследований». NOAA отмечает 200-летие. Национальное управление океанографии и атмосферы США. 2007-07-09.
- ^ Lenzen & Multauf 1964, стр. 324
- ^ Lenzen & Multauf 1964, стр. 329.
- ^ а б Вулард, Джордж П. (28–29 июня 1957 г.). «Гравитационные наблюдения во время МГГ». Геофизика и МГГ: Материалы симпозиума при открытии Международного геофизического года. Вашингтон, округ Колумбия: Американский геофизический союз, Национальная академия наук. п. 200. Получено 2009-05-27.
- ^ Lenzen & Multauf 1964, стр.336, рис.28
- ^ а б Майкл Р., Мэтьюз (2001). «Методология и политика в науке: судьба предложения Гюйгенса 1673 года о маятнике как международном стандарте длины и некоторые учебные предложения». Наука, образование и культура: вклад истории и философии науки. Springer. п. 296. ISBN 0-7923-6972-6.
- ^ Ренвик, Джеймс (1832). Элементы механики. Филадельфия: Кэри и Леа. стр.286–287.
- ^ Алдер, Кен (2003). Мера всего: семилетняя одиссея и скрытая ошибка, изменившие мир. США: Саймон и Шустер. п. 88. ISBN 978-0-7432-1676-0.
- ^ цитируется в Журдан, Луи (22 октября 2001 г.). "Re: СИ и словари". USMA (Список рассылки). Получено 2009-01-27.
- ^ Аньоли, Паоло; Джулио Д'Агостини (декабрь 2004 г.). «Почему счетчик бьет второй?». arXiv:физика / 0412078.
- ^ цитируется в ЛеКонт, Джон (август 1885 г.). «Метрическая система». Ежемесячный журнал Overland. 6 (2): 178. Получено 2009-03-04.
- ^ Зупко, 1990, с.131
- ^ Зупко, 1990, с.140-141.
- ^ Зупко, 1990, с.93
- ^ Шумахер, Генрих (1821). «Датский стандарт длины». Ежеквартальный журнал науки, литературы и искусства. 11 (21): 184–185. Получено 2009-02-17.
- ^ «Шумахер, Генрих Кристиан». Американская циклопедия. 14. D. Appleton & Co., Лондон. 1883. с. 686. Получено 2009-02-17.
- ^ Trautwine, Джон Крессон (1907). Записная книжка гражданского инженера, 18-е изд.. Нью-Йорк: Джон Вили. п. 216.
- ^ Мультяшный, Джон (8 сентября 2000 г.). «Вне времени: исследователи воссоздают эксперимент с часами 1665 года, чтобы получить представление о современных синхронизированных осцилляторах». Технологический институт Джорджии. Получено 2007-05-31.
- ^ А.Л. Фрадков, Б. Андриевский, "Синхронизация и фазовые соотношения в движении двух маятниковой системы", Международный журнал нелинейной механики, вып. 42 (2007), стр. 895–901.
- ^ И. Блехман, "Синхронизация в науке и технологии", ASME Press, Нью-Йорк, 1988 г. (Перевод с русского на английский)
- ^ Интересный симулятор движения кадило можно найти на этот сайт.
- ^ а б Харт, Мэтью (2 февраля 2016 г.). "Физика рискует смертью от разрушающего шара для науки". Ботаник. Получено 14 марта 2017.
- ^ Соренсон, Рой (2014). «Эксперименты с мыслями для новичков». В Бут, Энтони Роберт; Роуботтом, Даррелл П. (ред.). Интуиции. Oxford Univ Pr. п. 139. ISBN 9780199609192. Получено 15 марта 2017.
- ^ "Маятник шара для боулинга". Чудеса физики. Университет Висконсина-Мэдисона. Получено 14 марта 2017.
- ^ weknowmemes (8 августа 2014 г.). "Тест с физическим мячом прошел не так". YouTube. Получено 14 марта 2017.
- ^ Скотт, Джордж Райли (2009). История пыток на протяжении веков. Рутледж. п. 242. ISBN 978-1136191602.
- ^ а б Льоренте, Хуан Антонио (1826). История инквизиции Испании. Сокращенный и переведенный Джорджем Б. Уиттакером.. Оксфордский университет. С. XX, предисловие.
- ^ Эбботт, Джеффри (2006). Казнь: гильотина, маятник, тысяча порезов, испанский осел и 66 других способов казнить кого-то. Пресса Св. Мартина. ISBN 978-0-312-35222-6.
- ^ По, Эдгар Аллан (1842 г.). Яма и маятник. Книжная классика. ISBN 978-9635271900.
- ^ Рот, Сесил (1964). Испанская инквизиция. W. W. Norton and Company. стр.258. ISBN 978-0-393-00255-3.
маятник.
- ^ Манникс, Дэниел П. (2014). История пыток. eNet Press. п. 76. ISBN 978-1-61886-751-3.
- ^ а б Павлак, Брайан (2009). Охота на ведьм в западном мире: преследование и наказание со стороны инквизиции через Салемские процессы. ABC-CLIO. п. 152. ISBN 978-0-313-34874-7.
- ^ Юрченко, Д .; Алеврас, П. (2013). «Динамика N-маятника и ее применение в концепции волнового преобразователя энергии». Международный журнал динамики и управления. 1 (4): 4. Дои:10.1007 / s40435-013-0033-х.
дальнейшее чтение
- Г. Л. Бейкер и Дж. А. Блэкберн (2009). Маятник: пример из физики (Издательство Оксфордского университета).
- М. Гиттерман (2010). Хаотический маятник (Мировой научный).
- Майкл Р. Мэтьюз, Артур Стиннер, Колин Ф. Голд (2005)Маятник: научные, исторические, философские и образовательные перспективы, Springer
- Мэтьюз, Майкл Р .; Голд, Колин; Стиннер, Артур (2005). «Маятник: его место в науке, культуре и педагогике». Научное образование. 13 (4/5): 261–277. Bibcode:2004 г., научные и изд. 13..261M. Дои:10.1023 / b: sced.0000041867.60452.18. S2CID 195221704.
- Шломо Зильберманн, (2014) «Фундаментальный маятник; Путь в никуда» (книга)
Маттис, Роберт Дж. (2004). Точные часы с маятником. Великобритания: Oxford Univ. Нажмите. ISBN 978-0-19-852971-2.
- Нельсон, Роберт; М. Г. Олссон (февраль 1986 г.). «Маятник - богатая физика из простой системы». Американский журнал физики. 54 (2): 112–121. Bibcode:1986AmJPh..54..112N. Дои:10.1119/1.14703.
- Л. П. Пок (2011). Понимание маятников: краткое введение (Спрингер).
внешняя ссылка
![]() СМИ, связанные с Маятники в Wikimedia Commons
СМИ, связанные с Маятники в Wikimedia Commons

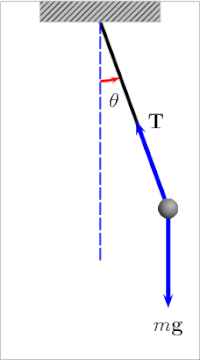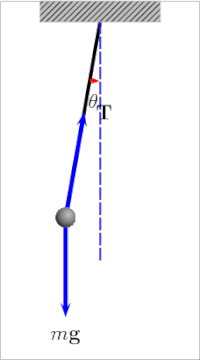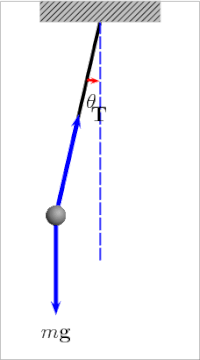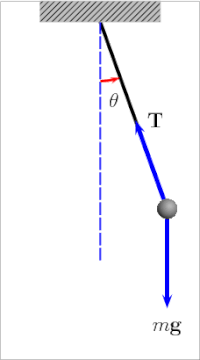








![{ displaystyle T = 2 pi { sqrt { frac {L} {g}}} left [ sum _ {n = 0} ^ { infty} left ({ frac { left (2n вправо)!} {2 ^ {2n} left (n! right) ^ {2}}} right) ^ {2} sin ^ {2n} left ({ frac { theta _ {0} } {2}} right) right] = 2 pi { sqrt { frac {L} {g}}} left (1 + { frac {1} {16}} theta _ {0} ^ {2} + { frac {11} {3072}} theta _ {0} ^ {4} + cdots right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8421cbd1dd0d5564c5f84120bb9f8a68e7e6312)