WikiDer > Спонтанное излучение
Спонтанное излучение это процесс, в котором квантово-механический система (например, молекула, атом или субатомная частица) проходит из возбужденное энергетическое состояние в более низкое энергетическое состояние (например, его основное состояние) и излучает квантованное количество энергии в виде фотон. Спонтанное излучение в конечном итоге отвечает за большую часть света, который мы видим вокруг нас; он настолько распространен, что существует множество названий, по сути, одного и того же процесса. Если атомы (или молекулы) возбуждаются другими способами, кроме нагрева, спонтанное излучение называется свечение. Например, светлячки светятся. И есть разные формы люминесценции в зависимости от того, как образуются возбужденные атомы (электролюминесценция, хемилюминесценция так далее.). Если на возбуждение влияет поглощение излучения, спонтанное излучение называется флуоресценция. Иногда молекулы имеют метастабильный уровень и продолжают флуоресцировать еще долгое время после выключения возбуждающего излучения; это называется фосфоресценция. Фигурки, которые светятся в темноте, фосфоресцируют. Лазеры начать через спонтанное излучение, затем в непрерывном режиме работы стимулированное излучение.
Спонтанное излучение нельзя объяснить классическая теория электромагнетизма и по сути является квантовым процессом. Первым человеком, точно определившим скорость спонтанного излучения из первых принципов, был Дирак в своей квантовой теории излучения,[1] предшественник теории, которую он позже назвал квантовая электродинамика.[2] Когда современных физиков просят дать физическое объяснение спонтанного излучения, они обычно ссылаются на энергия нулевой точки электромагнитного поля.[3][4] В 1963 г. Модель Джейнса – Каммингса[5] была разработана описывающая система двухуровневый атом взаимодействует с квантованной модой поля (то есть с вакуумом) внутри оптического резонатора. Это дало неинтуитивное предсказание, что скорость спонтанного излучения можно контролировать в зависимости от граничных условий окружающего вакуумного поля. Эти эксперименты привели к квантовая электродинамика резонатора (CQED), изучение влияния зеркал и резонаторов на радиационные поправки.
Вступление
Если источник света («атом») находится в возбужденном состоянии с энергией , он может самопроизвольно распадаться на более низкий уровень (например, в основное состояние) с энергией , высвобождая разницу в энергии между двумя состояниями в виде фотона. Фотон будет иметь угловая частота и энергия :
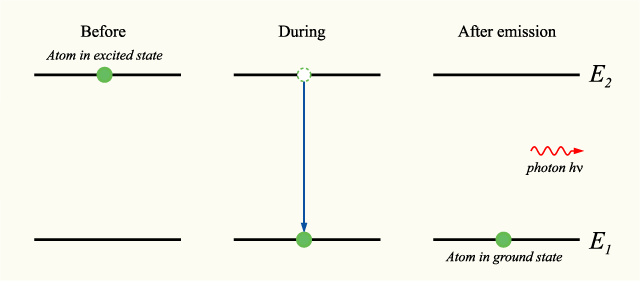
куда это приведенная постоянная Планка. Примечание: , куда это Постоянная Планка и линейный частота. В фаза Спонтанное излучение фотона является случайным, как и направление, в котором фотон распространяется. Это неверно для стимулированное излучение. Диаграмма уровней энергии, иллюстрирующая процесс спонтанного излучения, показана ниже:
Если количество источников света в возбужденном состоянии в момент времени дан кем-то , скорость, с которой распадается:
куда - скорость спонтанного излучения. В уравнении скорости - константа пропорциональности для этого конкретного перехода в данном конкретном источнике света. Константа называется Коэффициент Эйнштейна, и имеет единицы .[6] Приведенное выше уравнение можно решить, чтобы получить:
куда - начальное количество источников света в возбужденном состоянии, время и - скорость радиационного распада перехода. Количество возбужденных состояний таким образом, экспоненциально затухает со временем, подобно радиоактивный распад. После одного времени жизни количество возбужденных состояний уменьшается до 36,8% от исходного значения (-время). Скорость радиационного распада обратно пропорционально времени жизни :
Теория
Спонтанные переходы не могли быть объяснены в рамках Уравнение Шредингера, в котором квантовались электронные уровни энергии, а электромагнитное поле - нет. При условии, что собственные состояния атома правильно диагонализованы, перекрытие волновых функций между возбужденным состоянием и основным состоянием атома равно нулю. Таким образом, в отсутствие квантованного электромагнитного поля атом возбужденного состояния не может распасться до основного состояния. Чтобы объяснить спонтанные переходы, квантовая механика должна быть расширена до квантовая теория поля, в котором электромагнитное поле квантуется в каждой точке пространства. Квантовая теория поля электронов и электромагнитных полей известна как квантовая электродинамика.
В квантовой электродинамике (или КЭД) электромагнитное поле имеет основное состояние, то QED вакуум, которые могут смешиваться с возбужденными стационарными состояниями атома.[2] В результате этого взаимодействия «стационарное состояние» атома перестает быть истинным. собственное состояние комбинированной системы атом плюс электромагнитное поле. В частности, переход электрона из возбужденного состояния в основное электронное состояние смешивается с переходом электромагнитного поля из основного состояния в возбужденное состояние, т.е. состояние поля с одним фотоном в нем. Спонтанное излучение в свободном пространстве зависит от колебания вакуума для начала.[7][8]
Хотя существует только один электронный переход из возбужденного состояния в основное состояние, есть много способов, которыми электромагнитное поле может перейти из основного состояния в однофотонное состояние. То есть электромагнитное поле имеет бесконечно больше степеней свободы, соответствующих различным направлениям, в которых может излучаться фотон. Точно так же можно сказать, что фазовое пространство предлагаемое электромагнитным полем бесконечно больше, чем предлагаемое атомом. Эта бесконечная степень свободы излучения фотона приводит к кажущемуся необратимому распаду, то есть к спонтанному излучению.
При наличии электромагнитных вакуумных мод объединенная система атом-вакуум объясняется суперпозицией волновых функций атома в возбужденном состоянии без фотона и атома в основном состоянии с одним излучаемым фотоном:
куда и - волновая функция электромагнитного вакуума в возбужденном состоянии атома и ее вероятностная амплитуда, и атом в основном состоянии с одним фотоном (моды ) волновая функция и ее амплитуда вероятности, - частота атомного перехода, а - частота фотона. Сумма окончена и - волновое число и поляризация излучаемого фотона соответственно. Как упоминалось выше, испускаемый фотон может испускаться с разными волновыми числами и поляризациями, и результирующая волновая функция является суперпозицией этих возможностей. Для вычисления вероятности нахождения атома в основном состоянии (), необходимо решить временную эволюцию волновой функции с помощью подходящего гамильтониана.[1] Чтобы найти амплитуду перехода, необходимо усреднить (проинтегрировать) все вакуумные моды, поскольку необходимо учитывать вероятности того, что испускаемый фотон равномерно занимает различные части фазового пространства. «Спонтанно» испускаемый фотон имеет бесконечное количество различных мод для распространения, таким образом, вероятность того, что атом повторно поглотит фотон и вернется в исходное состояние, пренебрежимо мала, что делает распад атома практически необратимым. Такая необратимая временная эволюция системы атом-вакуум ответственна за кажущийся спонтанный распад возбужденного атома. Если бы нужно было отслеживать все вакуумные моды, комбинированная атомно-вакуумная система претерпела бы единичную временную эволюцию, что сделало бы процесс распада обратимым. Квантовая электродинамика резонатора является одной из таких систем, в которой модифицируются вакуумные моды, приводящие к обратимому процессу распада, см. также Квантовое возрождение. Теория спонтанного излучения в рамках КЭД была впервые рассчитана Вайскопфом и Вигнером.
В спектроскопии часто можно обнаружить, что атомы или молекулы в возбужденных состояниях рассеивают свою энергию в отсутствие какого-либо внешнего источника фотонов. Это не спонтанное излучение, а фактически безызлучательная релаксация атомов или молекул, вызванная флуктуацией окружающих молекул, находящихся внутри объема.[требуется разъяснение]
Скорость спонтанного излучения
Скорость спонтанного излучения (т.е. скорость излучения) может быть описана как Золотое правило Ферми.[9] Скорость излучения зависит от двух факторов: «атомной части», которая описывает внутреннюю структуру источника света, и «полевой части», которая описывает плотность электромагнитных мод окружающей среды. Атомная часть описывает силу перехода между двумя состояниями с точки зрения моментов перехода. В однородной среде, например свободное место, скорость спонтанного излучения в дипольном приближении определяется выражением:
куда - частота излучения, это показатель преломления, это дипольный момент перехода, это диэлектрическая проницаемость вакуума, это приведенная постоянная Планка, это вакуум скорость света, и это постоянная тонкой структуры. Выражение обозначает определение дипольного момента перехода для оператора дипольного момента , куда это элементарный заряд и означает оператор позиции. (Это приближение не работает в случае электронов внутренней оболочки в атомах с высоким Z). Вышеприведенное уравнение ясно показывает, что скорость спонтанного излучения в свободном пространстве увеличивается пропорционально .
В отличие от атомов, которые имеют дискретный спектр излучения, квантовые точки можно непрерывно настраивать, изменяя их размер. Это свойство использовалось для проверки -частотная зависимость скорости спонтанного излучения, описываемая золотым правилом Ферми.[10]
Радиационный и безызлучательный распад: квантовая эффективность
В приведенном выше уравнении скорости предполагается, что уменьшение числа возбужденных состояний происходит только при излучении света. В этом случае говорят о полном радиационном распаде, а это означает, что квантовая эффективность составляет 100%. Помимо радиационного распада, который происходит при излучении света, существует второй механизм распада; безызлучательный распад. Для определения общей скорости распада , радиационные и безызлучательные скорости следует суммировать:
куда - полная скорость распада, - скорость радиационного распада, а скорость безызлучательного распада. Квантовая эффективность (QE) определяется как доля процессов излучения, в которых участвует излучение света:
При безызлучательной релаксации энергия выделяется как фононы, более известный как высокая температура. Безызлучательная релаксация происходит, когда разность энергий между уровнями очень мала и обычно происходит в гораздо более быстром масштабе времени, чем радиационные переходы. Для многих материалов (например, полупроводники), электроны быстро перемещаются с высокого энергетического уровня на метастабильный уровень посредством небольших безызлучательных переходов, а затем совершают окончательное движение вниз на нижний уровень через оптический или радиационный переход. Этот последний переход - переход через запрещенная зона в полупроводниках. Большие безызлучательные переходы происходят нечасто, поскольку Кристальная структура обычно не может выдерживать большие колебания без разрушения связей (что обычно не происходит при расслаблении). Мета-стабильные состояния образуют очень важную особенность, которая используется при строительстве лазеры. В частности, поскольку электроны из них медленно распадаются, их можно намеренно накапливать в этом состоянии без особых потерь, а затем стимулированное излучение может использоваться для усиления оптического сигнала.
Смотрите также
- Поглощение (оптика)
- Вынужденное излучение
- Спектр излучения
- Спектральная линия
- Атомная спектральная линия
- Лазерная наука
- Эффект Перселла
- Фотонный кристалл
- Вакуумные колебания Раби
- Модель Джейнса – Каммингса
Рекомендации
- ^ а б Дирак, Поль Адриан Морис (1927). «Квантовая теория излучения и поглощения излучения». Proc. Рой. Soc. A114 (767): 243–265. Bibcode:1927RSPSA.114..243D. Дои:10.1098 / RSPA.1927.0039.
- ^ а б Милонни, Питер В. (1984). "Почему спонтанное излучение?" (PDF). Являюсь. J. Phys. 52 (4): 340. Bibcode:1984AmJPh..52..340M. Дои:10.1119/1.13886.
- ^ Вайскопф, Виктор (1935). "Probleme der neueren Quantentheorie des Elektrons". Naturwissenschaften. 23: 631–637. Bibcode:1935NW ..... 23..631W. Дои:10.1007 / BF01492012.
- ^ Велтон, Теодор Аллен (1948). «Некоторые наблюдаемые эффекты квантово-механических колебаний электромагнитного поля». Phys. Rev. 74 (9): 1157. Bibcode:1948PhRv ... 74.1157W. Дои:10.1103 / PhysRev.74.1157.
- ^ Jaynes, E.T .; Каммингс, Ф. В. (1963). «Сравнение квантовой и полуклассической теорий излучения применительно к пучковому мазеру». Труды IEEE. 51 (1). Дои:10.1109 / PROC.1963.1664.
- ^ Р. Лаудон, Квантовая теория света, 3-е изд. (Oxford University Press Inc., Нью-Йорк, 2001).
- ^ Хироюки Ёкояма и Удихара К. (1995). Спонтанное излучение и лазерная генерация в микрополостях. Бока-Ратон: CRC Press. п. 6. ISBN 0-8493-3786-0.
- ^ Мариан О Скалли и М. Сухайль Зубайри (1997). Квантовая оптика. Кембридж, Великобритания: Издательство Кембриджского университета. п. §1.5.2 с. 22–23. ISBN 0-521-43595-1.
- ^ Б. Хендерсон, Дж. Имбуш, Оптическая спектроскопия неорганических твердых тел (Кларендон Пресс, Оксфорд, Великобритания, 1989).
- ^ А. Ф. ван Дриэль, Г. Аллан, К. Делеру, П. Лодаль, В. Л. Вос и Д. Ванмакельберг, Частотно-зависимая скорость спонтанного излучения нанокристаллов CdSe и CdTe: влияние темных состояний, Physical Review Letters, 95, 236804 (2005).http://cops.tnw.utwente.nl/pdf/05/PHYSICAL%20REVIEW%20LETTERS%2095%20236804%20(2005).pdf