WikiDer > Уравнение Ван Деемтера
В уравнение ван деемтера в хроматография, названный в честь Ян ван Деемтер, связывает отклонение на единицу длины разделительной колонны с линейным Мобильная фаза скорость с учетом физических, кинетических и термодинамических свойств разделения.[1] Эти свойства включают пути внутри столбца, распространение (осевой и продольный), и массообмен кинетика между стационарной и подвижной фазами. В жидкостной хроматографии скорость подвижной фазы принимается за выходную скорость, то есть отношение скорости потока в мл / с к площади поперечного сечения «пути потока на выходе из колонки». Для насадочной колонки величина Площадь поперечного сечения пути потока на выходе из колонки обычно принимается равной 0,6 площади поперечного сечения колонны. В качестве альтернативы линейная скорость может быть принята как отношение длины колонки к мертвому времени. Если подвижная фаза - газ, то давление необходимо применить исправление. Дисперсия на единицу длины столбца принимается как отношение длины столбца к эффективности столбца в теоретические тарелки. Уравнение Ван Деемтера - это гиперболическая функция предсказывает, что существует оптимальная скорость, при которой будет минимальное отклонение на единицу длины столбца и, следовательно, максимальная эффективность. Уравнение ван Деемтера явилось результатом первого применения скоростной теории к процессу хроматографического элюирования.
Уравнение Ван Деемтера
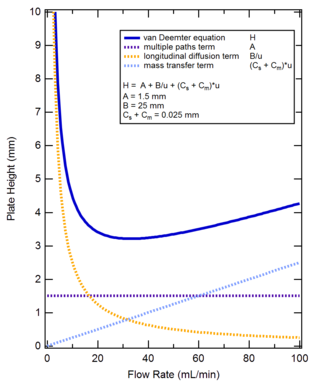
Уравнение ван Деемтера связывает высоту, эквивалентную теоретической тарелке (HETP) хроматографической колонки, с различными параметрами потока и кинетическими параметрами, которые вызывают уширение пиков, следующим образом:
Где
- HETP = мера разрешающей способности столбца [м]
- А = Вихревой диффузии параметр, связанный с каналом через неидеальную упаковку [м]
- B = коэффициент диффузии элюирующих частиц в продольном направлении, в результате чего разброс [м2 s−1]
- C = устойчивость к коэффициент массопереноса анализируемого вещества между подвижной и неподвижной фазами [ы]
- ты = скорость [РС−1]
В открытом трубчатый капилляры, член A будет равен нулю, поскольку отсутствие уплотнения означает, что образование каналов не происходит. В упакованных колонках, однако, существует несколько различных маршрутов («каналов») через упаковку колонки, что приводит к расширению полосы. В последнем случае A не будет нулем.
Форма уравнения Ван Деемтера такова, что HETP достигает минимального значения при определенной скорости потока. При такой скорости потока разрешающая способность колонки максимальна, хотя на практике время элюирования может оказаться непрактичным. Дифференцируя уравнение Ван Демтера по скорости, установив полученное выражение равным нулю и решив найти оптимальную скорость, получим следующее:
Количество тарелок
Высота пластины определяется как:
с длина столбца и количество теоретических тарелок можно оценить по хроматограмма путем анализа время удерживания для каждого компонента и его стандартное отклонение в качестве меры ширины пика при условии, что кривая элюирования представляет собой Кривая Гаусса.
В этом случае количество тарелок определяется по формуле:[2]
Используя более практичный ширина пика на половине высоты уравнение:
или шириной у основания козырька:
Расширенный фургон Deemter
Уравнение Ван Деемтера можно расширить до:[3]
Где:
- H - высота плиты
- λ - форма частицы (с учетом упаковки)
- dп диаметр частицы
- γ, ω и R - постоянные
- Dм это коэффициент диффузии мобильной фазы
- dc диаметр капилляра
- dж толщина пленки
- Ds - коэффициент диффузии неподвижной фазы.
- u - линейная скорость
Уравнение Родригеса
В Уравнение Родригеса, названный в честь Алирио Родригес, является расширением уравнения Ван-Демтера, используемого для описания эффективности слоя проницаемых (крупнопористых) частиц.[4]
Уравнение:
куда
и внутричастный Число Пекле.
Смотрите также
Рекомендации
- ^ ван Деемтер JJ, Zuiderweg FJ и Klinkenberg A (1956). «Продольная диффузия и сопротивление массопереносу как причины неидеальности в хроматографии». Chem. Англ. Sci. 5: 271–289. Дои:10.1016/0009-2509(56)80003-1.
- ^ ИЮПАК, Сборник химической терминологии, 2-е изд. («Золотая книга») (1997). Исправленная онлайн-версия: (2006–) "государственный номер, N". Дои:10.1351 / goldbook.P04694
- ^ Казакевич, Юрий. «Теория расширения полосы (уравнение Ван Деемтера)». Университет Сетон Холл. Получено 5 февраля 2014.
- ^ Алирио Э. Родригес (10 октября 1997 года). «Проницаемые насадки и перфузионная хроматография в разделении белков». Журнал хроматографии B. 699 (1–2): 47–61. Дои:10.1016 / S0378-4347 (97) 00197-7.














![{ displaystyle f ( lambda) = { frac {3} { lambda}} left [{ frac {1} { tanh ( lambda)}} - { frac {1} { lambda}} верно]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5beb8548a472afdc6f139e90cbe8344efa341704)
