WikiDer > Ведьма Агнези

Witch of Agnesi
Не путать с Ведьма Эндора или же Король-чародей Ангмара.

Ведьма Агнеси с параметрами а = 1, а = 2, а = 4, и а = 8

В математика, то ведьма Аньези (Итальянское произношение:[aɲˈɲeːzi]) это кривая в кубической плоскости определяется из двух диаметрально противоположных точек окружности. Он получил свое название от итальянского математика. Мария Гаэтана Аньези, и из-за неправильного перевода итальянского слова для шкатулка. До Агнеси ту же кривую изучал Ферма, Гранди, и Ньютон.

В график производной от арктангенс функция образует пример ведьмы Агнеси. функция плотности вероятности из Распределение Коши, ведьма Агнеси находит применение в теория вероятности. Это также порождает Феномен Рунге в приближении функций полиномами, был использован для аппроксимации распределения энергии спектральные линии, и моделирует форму холмов.

Ведьма касается своего определяющего круга в одной из двух определяющих точек, и асимптотический к касательная к окружности в другой точке. Он имеет уникальный вершина (точка крайней кривизны) в точке касания с его определяющей окружностью, которая также является его соприкасающийся круг в таком случае. Он также имеет два конечных точки перегиба и одна бесконечная точка перегиба. Площадь между ведьмой и ее асимптотической линией в четыре раза больше площади определяющего круга, а объем вращения кривой вокруг ее определяющей линии в два раза больше объема кривой. тор вращения его определяющего круга.

Строительство

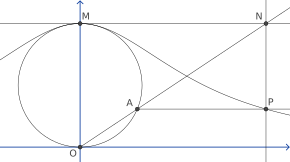
Ведьма Агнеси (кривая Депутат) с помеченными точками
Анимация, показывающая создание ведьмы Агнеси

Чтобы построить эту кривую, начните с любых двух точек О и Mи нарисуйте круг с помощью ОМ как диаметр. Для любой другой точки А по кругу пусть N быть точкой пересечения секущая линия OA и касательная в точке M.Позволять п быть точкой пересечения прямой, перпендикулярной к ОМ через А, и прямая, параллельная ОМ через N. потом п лежит на ведьме Агнеси. Ведьма состоит из всех точек п которые могут быть построены таким же образом из того же выбора О и M.[1] Он включает в качестве предельного случая точку M сам.

Уравнения

Предположим, что точка О находится на источник и указать M лежит на положительном у-ось, и круг диаметром ОМ имеет радиус аТогда ведьма, построенная из О и M имеет декартово уравнение[2][3]

Это уравнение можно упростить, выбрав а = 1/2 к виду

В упрощенном виде эта кривая представляет собой график из производная из арктангенс функция.[4]

Ведьму Агнеси также можно описать параметрические уравнения чей параметр θ угол между OM и OA, измеренный по часовой стрелке:[2][3]

Характеристики

Основные свойства этой кривой можно вывести из интегральное исчисление.Площадь между ведьмой и ее асимптотической линией в четыре раза больше площади фиксированного круга, .[2][3][5]В объем вращения ведьмы Агнези о своей асимптоте .[2] Это в два раза больше объема тор образованный вращением определяющего круга ведьмы вокруг той же линии.[5]

Кривая имеет уникальный вершина в точке касания с определяющей окружностью. То есть эта точка - единственная точка, где кривизна достигает локального минимума или локального максимума.[6] Определяющий круг ведьмы также является ее соприкасающийся круг в вершине,[7] уникальный круг, который «целует» кривую в этой точке, имея одинаковую ориентацию и кривизну.[8] Поскольку это соприкасающийся круг в вершине кривой, он имеет контакт третьего порядка с кривой.[9]

Кривая имеет два точки перегиба, в точках

соответствующие углам .[2][3] Если рассматривать как кривую в проективная плоскость есть также третья точка бесконечного перегиба в точке, где линия на бесконечности пересекает асимптотическая линия. Поскольку одна из ее точек перегиба бесконечна, ведьма имеет минимально возможное количество конечных реальных точек перегиба любой неособой кубической кривой.[10]

Самая большая площадь прямоугольник что может быть вписано между ведьмой и ее асимптотой , для прямоугольника, высота которого равна радиусу определяющего круга, а ширина в два раза больше диаметра круга.[5]

История

Ранние исследования

Иллюстрация Аньези 1748 года кривой и ее построения[11]

Кривая была изучена Пьер де Ферма в его трактате 1659 г. квадратура. В нем Ферма вычисляет площадь под кривой и (без подробностей) утверждает, что тот же метод распространяется и на циссоид диокла. Ферма пишет, что ему предложили кривую "ab erudito geometra"[ученым геометром].[12] Paradís, Pla & Viader (2008) предположить, что геометр, который предложил эту кривую Ферма, мог быть Антуан де Лалубер.[13]

Приведенная выше конструкция этой кривой была найдена Гранди (1718); такая же конструкция была обнаружена ранее Исаак Ньютон, но опубликовано только посмертно позже, в 1779 году.[14]Гранди (1718) также предложил название Versiera (на итальянском) или версориа (на латыни) для кривой. Латинский термин также используется для обозначения простынь, веревка, которая поворачивает парус, но Гранди, возможно, вместо этого имел в виду просто Версина функция, которая появилась в его конструкции.[5][14][15][16]

В 1748 г. Мария Гаэтана Аньези опубликовано Instituzioni analitiche ad uso della gioventù italiana, ранний учебник по исчисление.[11]В нем, предварительно рассмотрев две другие кривые, она включает исследование этой кривой. Она определяет кривую геометрически как геометрическое место точек, удовлетворяющих определенной пропорции, определяет ее алгебраическое уравнение и находит ее вершину, асимптотическую линию и точки перегиба.[17]

Этимология

Мария Гаэтана Аньези назвал кривую по Гранди, Versiera.[15][17] По совпадению, в то время в Италии было принято говорить о Дьявол, противник Бога, другими словами, как Aversiero или же Versiera, происходит от латинского противник. Versiera, в частности, использовался для обозначения жены дьявола или «ведьмы».[18] Из-за этого кембриджский профессор Джон Колсон неправильно перевел название кривой как «ведьма».[19] Различные современные работы об Агнеси и о кривой предполагают несколько разные догадки, как именно произошел этот неправильный перевод.[20][21] Струик упоминает, что:[17]

Слово [Versiera] происходит от латинского Vertere, повернуть, но также является сокращением итальянского Авверсьера, женщина-дьявол. Кто-то в Англии однажды перевел это слово как «ведьма», и этот глупый каламбур до сих пор с любовью сохраняется в большинстве наших учебников на английском языке. ... Кривая уже появилась в трудах Ферма (Oeuvres, I, 279–280; III, 233–234) и других; название Versiera от Гвидо Гранди (Quadratura circi et hyperbolae, Пиза, 1703 г.). Кривая имеет тип 63 в Ньютонклассификация. ... Первым, кто использовал термин «ведьма» в этом смысле, возможно, был Б. Уильямсон, Интегральное исчисление, 7 (1875), 173;[22] видеть Оксфордский словарь английского языка.

С другой стороны, Стивен Стиглер предполагает, что сам Гранди «, возможно, баловался игрой слов», двойной каламбур, соединяющий дьявола с версиной, а функцию синуса с формой женской груди (оба из которых могут быть написаны как «сено» по-итальянски) .[14]

Приложения

Масштабированная версия кривой - это функция плотности вероятности из Распределение Коши. Это распределение вероятностей на случайная переменная определяется следующими случайный эксперимент: для фиксированной точки выше -оси, выберите равномерно случайным образом линию через , и разреши быть координатой точки, в которой эта случайная линия пересекает ось. Распределение Коши имеет пиковое распределение, визуально напоминающее распределение нормальное распределение, но это тяжелые хвосты предотвратить это от ожидаемое значение по обычным определениям, несмотря на его симметрию. Что касается самой ведьмы, это означает, что -координата центроид области между кривой и ее асимптотической линией четко не определена, несмотря на симметрию этой области и ее конечную площадь.[14][23]

В числовой анализ, при приближении функций с помощью полиномиальная интерполяция с равноотстоящими точками интерполяции может случиться так, что для некоторых функций использование большего количества точек создает худшие приближения, так что интерполяция отклоняется от функции, которую она пытается аппроксимировать, а не сходится к ней. Это парадоксальное поведение называется Феномен Рунге. Впервые он был обнаружен Карл Давид Толме Рунге для функции Рунге , еще одна масштабированная версия ведьмы Агнеси, при интерполяции этой функции на интервале . То же самое происходит и с ведьмой. сам в более широком интервале .[24]

Ведьма Агнеси приближается к спектральное распределение энергии из спектральные линии, особенно рентгеновский снимок линий.[25]

Поперечное сечение гладкого холм имеет форму, похожую на ведьму.[26] Кривые этой формы использовались в качестве типового топографического препятствия в потоке при математическом моделировании.[27][28]Уединенные волны в глубокой воде тоже может принимать такую ​​форму.[29][30]

Вариант этой кривой использовался Готфрид Вильгельм Лейбниц вывести Формула Лейбница для π. Эта формула, бесконечная серия

можно получить, приравняв площадь под кривой к интегралу функции ,с использованием Серия Тейлор разложение этой функции как бесконечное геометрическая серия и поэтапная интеграция.[3]

В популярной культуре

Ведьма Агнеси - это название романа Роберта Спиллера. Он включает сцену, в которой учитель представляет версию истории семестра.[31]

Ведьма Агнези также название музыкального альбома джазового квартета Radius. На обложке альбома изображено сооружение ведьмы.[32]

Примечания

  1. ^ Орлы, Томас Генри (1885), "Ведьма Агнези", Конструктивная геометрия плоских кривых: с многочисленными примерами, Macmillan and Company, стр. 313–314.
  2. ^ а б c d е Лоуренс, Дж. Деннис (2013), "4.3 Ведьма Агнеси (Ферма, 1666; Агнеси, 1748)", Каталог специальных плоских кривых, Dover Books on Mathematics, Courier Corporation, стр. 90–93, ISBN 9780486167664
  3. ^ а б c d е Йейтс, Роберт С. (1954), «Ведьма из Агнеси», Кривые и их свойства (PDF), Классика в математическом образовании, 4, Национальный совет учителей математики, стр. 237–238.
  4. ^ Коэн, Дэвид В .; Хенле, Джеймс М. (2005), Исчисление: язык перемен, Jones & Bartlett Learning, стр. 351, ISBN 9780763729479
  5. ^ а б c d Ларсен, Гарольд Д. (январь 1946 г.), «Ведьма Агнези», Школьные науки и математика, 46 (1): 57–62, Дои:10.1111 / j.1949-8594.1946.tb04418.x
  6. ^ Гибсон, К. Г. (2001), Элементарная геометрия дифференцируемых кривых: введение для студентов, Кембридж: Издательство Кембриджского университета, Упражнение 9.1.9, с. 131, Дои:10.1017 / CBO9781139173377, ISBN 0-521-80453-1, МИСТЕР 1855907
  7. ^ Хафтендорн, Дёрте (2017), «4.1 Версия, die Hexenkurve», Kurven Erkunden und Verstehen (на немецком языке), Springer, стр. 79–91, Дои:10.1007/978-3-658-14749-5, ISBN 978-3-658-14748-8. Относительно соприкасающегося круга см., В частности, стр. 81: «Der erzeugende Kreis ist der Krümmungskreis der weiten Versiera in ihrem Scheitel».
  8. ^ Липсман, Рональд Л .; Розенберг, Джонатан М. (2017), Многовариантное исчисление с MATLAB®: с приложениями к геометрии и физике, Springer, стр. 42, ISBN 9783319650708, Круг «целует» кривую точно до второго порядка, поэтому получил название «соприкасающийся круг» (от латинского слова «поцелуй»).
  9. ^ Фукс Дмитрий; Табачников Серж (2007), Математический омнибус: тридцать лекций по классической математике, Провиденс, Род-Айленд: Американское математическое общество, стр. 142, Дои:10.1090 / mbk / 046, ISBN 978-0-8218-4316-1, МИСТЕР 2350979
  10. ^ Арнольд, В.И. (2005), «Принцип топологической экономии в алгебраической геометрии», Обзоры по современной математике, Серия лекций Лондонского математического общества, 321, Кембридж: Издательство Кембриджского университета, стр. 13–23, Дои:10.1017 / CBO9780511614156.003, МИСТЕР 2166922. См. В частности стр. 15–16.
  11. ^ а б Аньези, Мария Гаэтана (1748), Instituzioni analitiche ad uso della gioventú italiana См., В частности, проблему 3, стр. 380–382, и Рис.135.
  12. ^ де Ферма, Пьер (1891), Oevres (на латыни), 1, Gauthier-Villars et fils, pp. 280–285.
  13. ^ Paradís, Jaume; Пла, Жозеп; Viader, Pelegrí (2008), «Метод квадратуры Ферма», Revue d'Histoire des Mathématiques, 14 (1): 5–51, МИСТЕР 2493381
  14. ^ а б c d Стиглер, Стивен М. (Август 1974 г.), "Исследования по истории вероятности и статистики. XXXIII. Коши и ведьма Агнези: историческое примечание о распределении Коши", Биометрика, 61 (2): 375–380, Дои:10.1093 / biomet / 61.2.375, JSTOR 2334368, МИСТЕР 0370838
  15. ^ а б Трусделл, К. (1991), "Исправления и дополнения для" Марии Гаэтаны Агнеси"", Архив истории точных наук, 43 (4): 385–386, Дои:10.1007 / BF00374764, […] Nata da 'seni versi, che da me suole chiamarsi la Versiera на латиноамериканском перо Версория […]
  16. ^ Гранди, Г. (1718 г.), "Note al trattato del Galileo del moto naturale Accellerato", Опера ди Галилео Галилей (на итальянском), III, Флоренция, стр. 393. Как цитирует Стиглер (1974).
  17. ^ а б c Перевод работы Агнеси по этой кривой можно найти в: Струик, Дирк Дж. (1969), Справочник по математике, 1200–1800 гг., Кембридж, Массачусетс: Издательство Гарвардского университета, стр. 178–180.
  18. ^ Пьетро Фанфани, Vocabolario dell'uso toscano, п. 334
  19. ^ Mulcrone, T. F. (1957), "Имена кривой Агнеси", Американский математический ежемесячный журнал, 64 (5): 359–361, Дои:10.2307/2309605, JSTOR 2309605, МИСТЕР 0085163
  20. ^ Сингх, Саймон (1997), Загадка Ферма: эпические поиски решения величайшей математической задачи в мире, Нью-Йорк: Уокер и компания, стр.100, ISBN 0-8027-1331-9, МИСТЕР 1491363
  21. ^ Дорогой, Дэвид (2004), Универсальная книга математики: от абракадабры до парадоксов Зенона, Хобокен, Нью-Джерси: John Wiley & Sons, стр. 8, ISBN 0-471-27047-4, МИСТЕР 2078978
  22. ^ Оксфордский словарь английского языка, Oxford University Press, 2018, ведьма, п.2, 4 (е), получено 3 июля 2018, 1875 Б. Уильямсон Elem. Относиться. Интегральное исчисление vii. 173 Найдите область между ведьмой Агнеси и ее асимптота.
  23. ^ Александр, Дж. Маккензи (2012), «Теория принятия решений встречает ведьму Агнези», Журнал Философии, 109 (12): 712–727, Дои:10.5840 / jphil20121091233
  24. ^ Купиллари, Антонелла; Де Томас, Элизабет (весна 2007 г.), «Разоблачение ведьмовского поведения функции Рунге», Математика и компьютерное образование, 41 (2): 143–156, ProQuest 235858817
  25. ^ Спенсер, Рой С. (сентябрь 1940 г.), «Свойства ведьмы Агнеси - применение для подбора формы спектральных линий», Журнал Оптического общества Америки, 30 (9): 415, Bibcode:1940JOSA ... 30..415S, Дои:10.1364 / josa.30.000415
  26. ^ Коппин, П. А .; Брэдли, Э. Ф .; Финниган, Дж. Дж. (Апрель 1994 г.), "Измерения потока через удлиненный гребень и его зависимость от термической устойчивости: среднее поле", Метеорология пограничного слоя, 69 (1–2): 173–199, Bibcode:1994BoLMe..69..173C, Дои:10.1007 / bf00713302, Полезной общей формой формы холма является так называемый профиль Ведьмы Агнеси.
  27. ^ Снайдер, Уильям Х .; Томпсон, Роджер С .; Эскридж, Роберт Э .; Лоусон, Роберт Э .; Кастро, Ян П .; Lee, J. T .; Хант, Джулиан К. Р .; Огава, Ясуси (март 1985 г.), "Структура сильно стратифицированного потока над холмами: концепция разделения-обтекания", Журнал гидромеханики, 152 (–1): 249, Bibcode:1985JFM ... 152..249S, Дои:10,1017 / с0022112085000684
  28. ^ Лэмб, Кевин Г. (февраль 1994 г.), «Численное моделирование расслоенного невязкого обтекания гладкой преграды» (PDF), Журнал гидромеханики, 260 (–1): 1, Bibcode:1994JFM ... 260 .... 1л, Дои:10.1017 / s0022112094003411, заархивировано из оригинал (PDF) 6 января 2014 г.
  29. ^ Бенджамин, Т. Брук (сентябрь 1967 г.), «Внутренние волны постоянной формы в жидкостях большой глубины», Журнал гидромеханики, 29 (3): 559, Bibcode:1967JFM .... 29..559B, Дои:10.1017 / s002211206700103x
  30. ^ Нунан, Джули А .; Смит, Роджер К. (сентябрь 1985 г.), «Теории линейных и слабонелинейных внутренних волн, применяемые к волнам« ипомеи »», Геофизическая и астрофизическая гидродинамика, 33 (1–4): 123–143, Bibcode:1985GApFD..33..123N, Дои:10.1080/03091928508245426
  31. ^ Филлипс, Дэйв (12 сентября 2006 г.), «Местный учитель, автор математики в книги», Газета
  32. ^ Радиус - Ведьма Агнези (Plutonium Records, 2002), Discogs, получено 28 мая 2018

внешняя ссылка