WikiDer > Центр массы

Эта игрушка использует принципы центра масс, чтобы удерживать равновесие на пальце.

В физика, то центр массы распределения масса в космосе (иногда называемый точка баланса) - единственная точка, где взвешенный родственник должность распределенных массовых сумм к нулю. Это точка, к которой может быть приложена сила, чтобы вызвать линейное ускорение без угловое ускорение. Расчеты в механика часто упрощаются, когда формулируются относительно центра масс. Это гипотетическая точка, в которой можно предположить, что вся масса объекта сосредоточена для визуализации его движения. Другими словами, центр масс - это частичный эквивалент данного объекта для применения Законы движения Ньютона.

В случае одиночного жесткое тело, центр масс фиксируется по отношению к телу, и если тело имеет однородную плотность, то он будет расположен в центроид. Центр масс может находиться вне физического тела, как это иногда бывает у полый или объекты открытой формы, такие как подкова. В случае распределения отдельных тел, таких как планеты из Солнечная система, центр масс может не соответствовать положению какого-либо отдельного члена системы.

Центр масс является полезной точкой отсчета для расчетов в механика которые включают массы, распределенные в пространстве, такие как линейный и угловой момент планетных тел и динамика твердого тела. В орбитальная механика, уравнения движения планет формулируются как точечные массы расположены в центрах масс. В центр масс кадра является инерциальная система отсчета в котором центр масс системы покоится относительно начала системы координат.

История

Понятие «центр масс» в виде центр гравитации был впервые представлен великим древнегреческим физиком, математиком и инженером Архимед Сиракузский. Он работал с упрощенными предположениями о гравитации, которые составляют однородное поле, таким образом придя к математическим свойствам того, что мы теперь называем центром масс. Архимед показал, что крутящий момент оказал рычаг с помощью гирь, находящихся в разных точках вдоль рычага, то же самое, что было бы, если бы все гири были перемещены в одну точку - их центр масс. В работе с плавающими телами он продемонстрировал, что ориентация плавающего объекта - это та, которая делает его центр масс как можно ниже. Он разработал математические методы для нахождения центров масс однородных по плотности объектов различных четко определенных форм.^[1]

Более поздние математики, разработавшие теорию центра масс, включают: Папп Александрийский, Гвидо Убальди, Франческо Мауролико,^[2] Федерико Коммандино,^[3] Саймон Стевин,^[4] Лука Валерио,^[5] Жан-Шарль де ла Файль, Пол Гулдин,^[6] Джон Уоллис, Луи Карре, Пьер Вариньон, и Алексис Клеро.^[7]

Второй закон Ньютона переформулирован относительно центра масс в Первый закон Эйлера.^[8]

Определение

Центр масс - это уникальная точка в центре распределения массы в пространстве, которая имеет свойство, что взвешенные векторы положения относительно этой точки суммируются до нуля. По аналогии со статистикой, центр масс - это среднее положение распределения массы в пространстве.

Система частиц

В случае системы частиц п_я, я = 1, …, п , каждый с массой м_я которые расположены в пространстве с координатами р_я, я = 1, …, п , координаты р центра масс удовлетворяют условию

${ displaystyle sum _ {i = 1} ^ {n} m_ {i} ( mathbf {r} _ {i} - mathbf {R}) = mathbf {0}.}$

Решение этого уравнения для р дает формулу

${ displaystyle mathbf {R} = { frac {1} {M}} sum _ {i = 1} ^ {n} m_ {i} mathbf {r} _ {i},}$

где M представляет собой сумму масс всех частиц.

Непрерывный объем

Если распределение массы непрерывно с плотностью ρ (р) внутри твердого Q, то интеграл от взвешенных координат положения точек этого объема относительно центра масс р по объему V равен нулю, то есть

${ displaystyle iiint limits _ {Q} rho ( mathbf {r}) ( mathbf {r} - mathbf {R}) dV = 0.}$

Решите это уравнение относительно координат р чтобы получить

${ Displaystyle mathbf {R} = { frac {1} {M}} iiint limits _ {Q} rho ( mathbf {r}) mathbf {r} dV,}$

где M - полная масса в объеме.

Если непрерывное массовое распределение имеет равномерное плотность, что означает постоянство ρ, тогда центр масс совпадает с центроид объема.^[9]

Барицентрические координаты

Координаты р центра масс двухчастичной системы, п₁ и п₂, с массами м₁ и м₂ дан кем-то

${ displaystyle mathbf {R} = { frac {1} {m_ {1} + m_ {2}}} (m_ {1} mathbf {r} _ {1} + m_ {2} mathbf {r } _ {2}).}$

Пусть процент от общей массы, разделенный между этими двумя частицами, варьируется от 100%. п₁ и 0% п₂ через 50% п₁ и 50% п₂ до 0% п₁ и 100% п₂, то центр масс р движется по линии от п₁ к п₂. Процент массы в каждой точке можно рассматривать как проекционные координаты точки. р на этой линии и называются барицентрическими координатами. Другой способ интерпретации процесса - это механическое уравновешивание моментов относительно произвольной точки. В числителе указывается общий момент, который затем уравновешивается эквивалентной полной силой в центре масс. Его можно обобщить на три точки и четыре точки для определения проективных координат на плоскости и в пространстве соответственно.

Системы с периодическими граничными условиями.

Для частиц в системе с периодические граничные условия две частицы могут быть соседями, даже если они находятся на противоположных сторонах системы. Это часто происходит в молекулярная динамика моделирование, например, в котором кластеры образуются в случайных местах, а иногда соседние атомы пересекают периодическую границу. Когда кластер находится на периодической границе, наивный расчет центра масс будет неверным. Обобщенный метод вычисления центра масс периодических систем заключается в рассмотрении каждой координаты, Икс и у и / или z, как если бы он находился на круге, а не на линии.^[10] Расчет принимает каждую частицу Икс координирует и отображает его на угол,

${ displaystyle theta _ {я} = { гидроразрыва {x_ {i}} {x_ {max}}} 2 pi}$

где Икс_{Максимум} размер системы в Икс направление и ${ displaystyle x_ {i} in [0, x_ {max})}$. С этой точки зрения две новые точки ${ displaystyle ( xi _ {i}, zeta _ {i})}$ могут быть сгенерированы, которые могут быть взвешены массой частицы ${ displaystyle x_ {i}}$ для центра масс или с учетом значения 1 для геометрического центра:

${ Displaystyle хи _ {я} = соз ( тета _ {я})}$

${ Displaystyle zeta _ {я} = грех ( тета _ {я})}$

в ${ Displaystyle ( xi, zeta)}$ плоскости эти координаты лежат на окружности радиуса 1. Из набора ${ Displaystyle xi _ {я}}$ и ${ displaystyle zeta _ {я}}$ значения от всех частиц, средние ${ Displaystyle { overline { xi}}}$ и ${ displaystyle { overline { zeta}}}$ рассчитаны.

${ displaystyle { overline { xi}} = { frac {1} {M}} sum _ {i = 1} ^ {n} m_ {i} xi _ {i},}$

${ displaystyle { overline { zeta}} = { frac {1} {M}} sum _ {i = 1} ^ {n} m_ {i} zeta _ {i},}$

где M представляет собой сумму масс всех частиц.

Эти значения отображаются обратно в новый угол, ${ displaystyle { overline { theta}}}$, откуда Икс координату центра масс можно получить:

${ displaystyle { overline { theta}} = mathrm {atan2} (- { overline { zeta}}, - { overline { xi}}) + pi}$

${ displaystyle x_ {com} = x_ {max} { frac { overline { theta}} {2 pi}}}$

Этот процесс можно повторить для всех размеров системы, чтобы определить полный центр масс. Полезность алгоритма заключается в том, что он позволяет математикам определять, где находится «лучший» центр масс, вместо того, чтобы угадывать или использовать кластерный анализ «развернуть» кластер, охватывающий периодические границы. Если оба средних значения равны нулю, ${ Displaystyle ({ overline { xi}}, { overline { zeta}}) = (0,0)}$, тогда ${ displaystyle { overline { theta}}}$ не определено. Это правильный результат, потому что он возникает только тогда, когда все частицы точно равномерно расположены. В этом состоянии их Икс координаты математически идентичны в периодическая система.

Центр гравитации

Схема развивающей игрушки, которая балансирует на точке: центр масс (C) располагается ниже опоры (P)

Центр тяжести тела - это точка, вокруг которой результирующий крутящий момент из-за силы тяжести исчезает. Если гравитационное поле можно рассматривать как однородное, центр масс и центр тяжести будут одинаковыми. Однако для спутников, находящихся на орбите вокруг планеты, в отсутствие других крутящих моментов, приложенных к спутнику, небольшое изменение (градиент) гравитационного поля между более близкой (более сильной) и более удаленной (более слабой) планетой может привести к крутящий момент, который будет стремиться выровнять спутник так, чтобы его длинная ось была вертикальной. В таком случае важно проводить различие между центром тяжести и центром масс. Любое горизонтальное смещение между ними приведет к приложенному крутящему моменту.

Полезно отметить, что центр масс - это фиксированное свойство для данного твердого тела (например, без смещения или сочленения), тогда как центр тяжести может, кроме того, зависеть от его ориентации в неоднородной гравитационной поле. В последнем случае центр тяжести всегда будет располагаться несколько ближе к главному притягивающему телу по сравнению с центром масс, и, таким образом, он будет менять свое положение в интересующем теле при изменении его ориентации.

При исследовании динамики самолетов, транспортных средств и судов силы и моменты необходимо разрешать относительно центра масс. Это верно независимо от того, учитывается ли сама гравитация. Обращение к центру масс как к центру тяжести - это что-то вроде разговорного слова, но оно широко используется, и когда эффекты градиента силы тяжести незначительны, центр тяжести и центр массы одинаковы и используются взаимозаменяемо.

В физике преимущества использования центра масс для моделирования распределения массы можно увидеть, рассмотрев результирующий сил тяжести на сплошном теле. Рассмотрим тело Q объема V с плотностью ρ (р) в каждой точке р в томе. В параллельном гравитационном поле сила ж в каждой точке р дан кем-то,

${ displaystyle mathbf {f} ( mathbf {r}) = - dm , ​​g { vec {k}} = - rho ( mathbf {r}) dV , g { vec {k}} ,}$

где dm - масса в точке р, g - ускорение свободного падения, а k - единичный вектор, определяющий вертикальное направление. Выберите опорную точку. р в объеме и вычислить Равнодействующая сила и крутящий момент в этой точке,

${ displaystyle mathbf {F} = iiint limits _ {Q} mathbf {f} ( mathbf {r}) dV = iiint limits _ {Q} rho ( mathbf {r}) dV ( -g { vec {k}}) = - Mg { vec {k}},}$

и

${ Displaystyle mathbf {T} = iiint limits _ {Q} ( mathbf {r} - mathbf {R}) times mathbf {f} ( mathbf {r}) dV = iiint limits _ {Q} ( mathbf {r} - mathbf {R}) times (-g rho ( mathbf {r}) dV { vec {k}}) = left ( iiint limits _ { Q} rho ( mathbf {r}) ( mathbf {r} - mathbf {R}) dV right) times (-g { vec {k}}).}$

Если ориентир р выбирается так, чтобы он был центром масс, то

${ displaystyle iiint limits _ {Q} rho ( mathbf {r}) ( mathbf {r} - mathbf {R}) dV = 0,}$

что означает результирующий крутящий момент Т= 0. Поскольку результирующий крутящий момент равен нулю, тело будет двигаться, как будто это частица, масса которой сосредоточена в центре масс.

Выбрав центр тяжести в качестве опорной точки для твердого тела, гравитационные силы не будут вызывать тело вращаться, что означает, что вес тела можно рассматривать как быть сконцентрирован в центре массы.

Линейный и угловой момент

Линейный и угловой момент совокупности частиц можно упростить, измерив положение и скорость частиц относительно центра масс. Пусть система частиц п_я, я=1,...,п масс м_я находиться в координатах р_я со скоростями v_я. Выберите точку отсчета р и вычислить относительные векторы положения и скорости,

${ displaystyle mathbf {r} _ {i} = ( mathbf {r} _ {i} - mathbf {R}) + mathbf {R}, quad mathbf {v} _ {i} = { frac {d} {dt}} ( mathbf {r} _ {i} - mathbf {R}) + mathbf {v}.}$

Полный момент импульса и момент количества движения системы равны

${ displaystyle mathbf {p} = { frac {d} {dt}} left ( sum _ {i = 1} ^ {n} m_ {i} ( mathbf {r} _ {i} - mathbf {R}) right) + left ( sum _ {i = 1} ^ {n} m_ {i} right) mathbf {v},}$

и

${ displaystyle mathbf {L} = sum _ {i = 1} ^ {n} m_ {i} ( mathbf {r} _ {i} - mathbf {R}) times { frac {d} {dt}} ( mathbf {r} _ {i} - mathbf {R}) + left ( sum _ {i = 1} ^ {n} m_ {i} right) left [ mathbf { R} times { frac {d} {dt}} ( mathbf {r} _ {i} - mathbf {R}) + ( mathbf {r} _ {i} - mathbf {R}) раз mathbf {v} right] + left ( sum _ {i = 1} ^ {n} m_ {i} right) mathbf {R} times mathbf {v}}$

Если р выбран в качестве центра масс, эти уравнения упрощаются до

${ displaystyle mathbf {p} = m mathbf {v}, quad mathbf {L} = sum _ {i = 1} ^ {n} m_ {i} ( mathbf {r} _ {i} - mathbf {R}) times { frac {d} {dt}} ( mathbf {r} _ {i} - mathbf {R}) + sum _ {i = 1} ^ {n} m_ {i} mathbf {R} times mathbf {v}}$

где м - полная масса всех частиц, п - импульс, а L - угловой момент.

В Закон сохранения импульса предсказывает, что для любой системы, не подверженной внешним силам, импульс системы останется постоянным, что означает, что центр масс будет двигаться с постоянной скоростью. Это относится ко всем системам с классическими внутренними силами, включая магнитные поля, электрические поля, химические реакции и т. Д. Более формально это верно для любых внутренних сил, которые сокращаются в соответствии с Третий закон Ньютона.^[11]

Определение центра масс

Метод отвеса

Экспериментальное определение центра масс тела использует силы тяжести, действующие на тело, и полагается на тот факт, что в параллельном гравитационном поле у ​​поверхности Земли центр масс совпадает с центром тяжести.

На этой оси должен лежать центр масс тела с осью симметрии и постоянной плотности. Таким образом, центр масс кругового цилиндра постоянной плотности имеет центр масс на оси цилиндра. Точно так же центр масс сферически-симметричного тела постоянной плотности находится в центре сферы. В общем, для любой симметрии тела его центр масс будет фиксированной точкой этой симметрии.^[12]

В двух измерениях

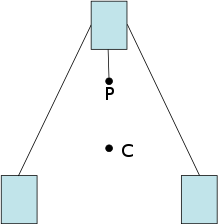
Экспериментальный метод определения центра масс состоит в том, чтобы подвесить объект в двух местах и ​​бросить отвес от точек подвеса. Пересечение двух линий - центр масс.^[13]

Форма объекта может быть уже определена математически, но может быть слишком сложной для использования известной формулы. В этом случае можно подразделить сложную форму на более простые, более элементарные формы, центры масс которых легко найти. Если общая масса и центр масс могут быть определены для каждой области, то центр масс всего является средневзвешенным значением центров.^[14] Этот метод может работать даже с объектами с отверстиями, которые можно рассматривать как отрицательные массы.^[15]

Прямое развитие планиметр известный как целочисленный граф или целочисленный счетчик, может использоваться для определения положения центроид или центр масс неправильной двухмерной формы. Этот метод может быть применен к фигуре с неровной, гладкой или сложной границей, где другие методы слишком сложны. Его регулярно использовали судостроители для сравнения с требуемым смещение и центр плавучести корабля и убедитесь, что он не перевернется.^[16][17]

В трех измерениях

Экспериментальный метод определения трехмерных координат центра масс начинается с поддержки объекта в трех точках и измерения сил, F₁, F₂, и F₃ которые выдерживают вес объекта, ${ displaystyle mathbf {W} = -W mathbf { hat {k}}}$ (${ displaystyle mathbf { hat {k}}}$ - единичный вектор в вертикальном направлении). Позволять р₁, р₂, и р₃ - координаты положения опорных точек, тогда координаты р центра масс удовлетворяют условию, что результирующий крутящий момент равен нулю,

${ displaystyle mathbf {T} = ( mathbf {r} _ {1} - mathbf {R}) times mathbf {F} _ {1} + ( mathbf {r} _ {2} - mathbf {R}) times mathbf {F} _ {2} + ( mathbf {r} _ {3} - mathbf {R}) times mathbf {F} _ {3} = 0,}$

или

${ displaystyle mathbf {R} times (-W mathbf { hat {k}}) = mathbf {r} _ {1} times mathbf {F} _ {1} + mathbf {r} _ {2} times mathbf {F} _ {2} + mathbf {r} _ {3} times mathbf {F} _ {3}.}$

Это уравнение дает координаты центра масс р* в горизонтальной плоскости как,

${ displaystyle mathbf {R} ^ {*} = - { frac {1} {W}} mathbf { hat {k}} times ( mathbf {r} _ {1} times mathbf { F} _ {1} + mathbf {r} _ {2} times mathbf {F} _ {2} + mathbf {r} _ {3} times mathbf {F} _ {3}). }$

Центр масс лежит на вертикальной прямой L, определяемой выражением

${ displaystyle mathbf {L} (t) = mathbf {R} ^ {*} + t mathbf { hat {k}}.}$

Трехмерные координаты центра масс определяются путем двукратного проведения этого эксперимента с объектом, расположенным так, чтобы эти силы измерялись для двух различных горизонтальных плоскостей, проходящих через объект. Центром масс будет пересечение двух прямых L₁ и я₂ полученные из двух экспериментов.

Приложения

Инженерные проекты

Автомобильные приложения

Инженеры пытаются спроектировать спортивная машина чтобы его центр масс был опущен, чтобы автомобиль ручка лучше, чтобы сохранить сцепление с дорогой при выполнении относительно крутых поворотов.

Характерная сдержанность американских военных Humvee был разработан частично так, чтобы он мог наклоняться дальше, чем более высокие автомобили, без перекатывать, потому что его низкий центр масс оставался бы над пространством, ограниченным четырьмя колесами, даже под углами, далекими от горизонтальный.

Аэронавтика

Центр масс - важная точка на самолет, что существенно влияет на устойчивость самолета. Чтобы самолет был достаточно устойчивым для безопасного полета, центр масс должен находиться в определенных пределах. Если центр масс впереди лимит вперед, самолет будет менее маневренным, возможно, до такой степени, что он не сможет развернуться для взлета или осветить при посадке.^[18] Если центр масс находится за задним пределом, самолет будет более маневренным, но также менее устойчивым и, возможно, достаточно нестабильным, чтобы его было невозможно летать. Момент рука лифт также будет уменьшено, что затрудняет восстановление после остановился состояние.^[19]

За вертолеты в парить, центр масс всегда находится прямо под роторная головка. В прямом полете центр масс будет двигаться вперед, чтобы уравновесить отрицательный крутящий момент по тангажу, создаваемый приложением циклический управление движением вертолета вперед; следовательно, крейсерский вертолет летит «носом вниз» в горизонтальном полете.^[20]

Астрономия

Два тела вращаются вокруг своих барицентр (красный Крест)

Центр масс играет важную роль в астрономии и астрофизике, где его обычно называют центром масс. барицентр. Барицентр - это точка между двумя объектами, где они уравновешивают друг друга; это центр масс, где два или более небесных тела орбита друг друга. Когда Луна орбиты планета, или планета вращается вокруг звезда, оба тела фактически вращаются вокруг точки, находящейся далеко от центра основного (большего) тела.^[21] Например, Луна не вращается вокруг точного центра Земля, но точка на линии между центром Земли и Луной, примерно на 1710 км (1062 мили) ниже поверхности Земли, где их массы уравновешиваются. Это точка, вокруг которой вращаются Земля и Луна, когда они движутся вокруг солнце. Если массы более похожи, например, Плутон и Харон, центр тяжести выйдет за пределы обоих тел.

Оснастка и безопасность

Зная расположение центра тяжести, когда оснастка имеет решающее значение и при неправильном предположении может привести к серьезным травмам или смерти. Центр тяжести, находящийся в точке подъема или выше, скорее всего, приведет к опрокидыванию. В целом, чем дальше центр тяжести ниже точки захвата, тем безопаснее подъемник. Следует учитывать и другие факторы, такие как смещение нагрузок, сила нагрузки и масса, расстояние между точками захвата и количество точек захвата. В частности, при выборе точек подъема очень важно располагать центр тяжести в центре и значительно ниже точек подъема.^[22]

Движение тела

В кинезиологии и биомеханике центр масс является важным параметром, который помогает людям понять свои человеческие передвижения. Как правило, центр масс человека обнаруживается одним из двух методов: Метод доски реакции - это статический анализ, в котором человек лежит на этом инструменте и использует его статическое равновесие уравнение для нахождения их центра масс; метод сегментации основан на математическом решении, основанном на физический принцип что суммирование из крутящие моменты отдельных участков тела, относительно указанный ось, должен равняться крутящему моменту всей системы, составляющей тело, измеренному относительно той же оси.^[23]

Смотрите также

Примечания

использованная литература

• Азимов Исаак (1988) [1966], Понимание физики, Barnes & Noble Books, ISBN 978-0-88029-251-1
• Бай, Линге; Брин, Дэвид (2008). «Расчет центра масс в неограниченной двумерной среде». Журнал графики, графического процессора и игровых инструментов. 13 (4): 53–60. Дои:10.1080 / 2151237X.2008.10129266. S2CID 40807367.
• Барон, Маргарет Э. (2004) [1969], Истоки исчисления бесконечно малых, Courier Dover Publications, ISBN 978-0-486-49544-6
• Битти, Миллард Ф. (2006), Основы инженерной механики, Том 2: Динамика - Анализ движения, Математические концепции и методы в науке и технике, 33, Спрингер, ISBN 978-0-387-23704-6
• Де Сильва, Кларенс В. (2002), Справочник по вибрации и ударам, CRC Press, ISBN 978-0-8493-1580-0
• Федеральная авиационная администрация (2007), Справочник по весу и балансировке самолета (PDF), Государственная типография США, заархивировано из оригинал (PDF) на 2011-10-19, получено 2011-10-23
• Фейнман, Ричард; Лейтон, Роберт Б.; Пески, Мэтью (1963), Лекции Фейнмана по физике, 1 (Шестое издание, февраль 1977 г.), Addison-Wesley, ISBN 978-0-201-02010-6
• Фраучи, Стивен С.; Оленик, Ричард П .; Апостол, Том М.; Гудштейн, Дэвид Л. (1986), Механическая вселенная: механика и тепло, расширенное издание, Издательство Кембриджского университета, ISBN 978-0-521-30432-0
• Джамбаттиста, Алан; Ричардсон, Бетти Маккарти; Ричардсон, Роберт Коулман (2007), Колледж физики, 1 (2-е изд.), Высшее образование Макгроу-Хилл, ISBN 978-0-07-110608-5
• Гольдштейн, Герберт; Пул, Чарльз; Сафко, Джон (2001), Классическая механика (3-е изд.), Эддисон Уэсли, ISBN 978-0-201-65702-9
• Гольдштейн, Герберт; Пул, Чарльз; Сафко, Джон (2002), Классическая механика (3-е изд.), Эддисон-Уэсли, ISBN 978-0-201-65702-9
• Гудман, Лоуренс Э .; Уорнер, Уильям Х. (2001) [1964], Статика, Дувр, ISBN 978-0-486-42005-9
• Хэмилл, Патрик (2009), Промежуточная динамика, Jones & Bartlett Learning, ISBN 978-0-7637-5728-1
• Jong, I.G .; Роджерс, Б. Г. (1995), Инженерная механика: статика, Издательство Saunders College Publishing, ISBN 978-0-03-026309-5
• Клеппнер, Даниэль; Коленков, Роберт (1973), Введение в механику (2-е изд.), Макгроу-Хилл, ISBN 978-0-07-035048-9
• Леви, Марк (2009), Математическая механика: использование физических рассуждений для решения проблем, Издательство Принстонского университета, ISBN 978-0-691-14020-9
• Манкосу, Паоло (1999), Философия математики и математическая практика в семнадцатом веке, Издательство Оксфордского университета, ISBN 978-0-19-513244-1
• Милликен, Роберт Эндрюс (1902), Механика, молекулярная физика и тепло: двенадцатинедельный курс в колледже, Чикаго: Скотт, Форсман и компания, получено 2011-05-25
• Мюррей, Карл; Дермотт, Стэнли (1999), Динамика солнечной системы, Издательство Кембриджского университета, ISBN 978-0-521-57295-8
• О'Доннелл, Питер Дж. (2015), Основная динамика и теория относительности, CRC Press, ISBN 978-1-466-58839-4
• Поллард, Дэвид Д.; Флетчер, Раймонд С. (2005), Основы структурной геологии, Издательство Кембриджского университета, ISBN 978-0-521-83927-3
• Пытель, Андрей; Киусалаас, Яан (2010), Инженерная механика: статика, 1 (3-е изд.), Cengage Learning, ISBN 978-0-495-29559-4
• Розен, Джо; Готард, Лиза Куинн (2009), Энциклопедия физических наук, Издательство информационной базы, ISBN 978-0-8160-7011-4
• Сангвин, Кристофер Дж. (2006), «Определение центра масс механическими средствами» (PDF), Журнал Oughtred общества, 15 (2), заархивировано оригинал (PDF) на 2011-10-05, получено 2011-10-23
• Serway, Raymond A .; Джуэтт, Джон В. (2006), Принципы физики: текст, основанный на исчислении, 1 (4-е изд.), Thomson Learning, Bibcode:2006ppcb.book ..... J, ISBN 978-0-534-49143-7
• Ширли, Джеймс Н .; Фэрбридж, Родос Уитмор (1997), Энциклопедия планетных наук, Спрингер, ISBN 978-0-412-06951-2
• Шор, Стивен Н. (2008), Силы в физике: историческая перспектива, Гринвуд Пресс, ISBN 978-0-313-33303-3
• Саймон, Кейт Р. (1971), Механика (3-е изд.), Эддисон-Уэсли, ISBN 978-0-201-07392-8
• Типлер, Пол А .; Моска, Джин (2004), Физика для ученых и инженеров, 1А (5-е изд.), W.H. Freeman and Company, ISBN 978-0-7167-0900-8
• Ван Пелт, Майкл (2005), Космический туризм: приключения на околоземной орбите и за ее пределами, Спрингер, ISBN 978-0-387-40213-0
• Винт, Питер (2003), «ЛАБОРАТОРИЯ: Центр масс (центр тяжести) человеческого тела» (PDF), КИН 335 - Биомеханика, получено 2013-10-18
• Уолтон, Уильям (1855), Сборник задач для иллюстрации основ теоретической механики. (2-е изд.), Deighton, Bell & Co.

внешняя ссылка

Искать барицентр в Викисловаре, бесплатном словаре.

• Движение центра масс показывает, что движение центра масс объекта при свободном падении такое же, как движение точечного объекта.
• Барицентр Солнечной системы, моделирование, показывающее влияние каждой планеты на барицентр Солнечной системы.
• Центр тяжести в работе, видео, показывающее, как объекты самостоятельно поднимаются по склону.