WikiDer > Икосаэдр со сжатием ребер
| Икосаэдр со сжатием ребер | |
|---|---|
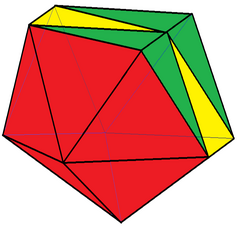 | |
| Лица | 18 треугольники |
| Края | 27 |
| Вершины | 11 |
| Симметрия | C2v, [2], (* 22), порядок 4 |
| Конфигурация вершины | 2 (34) 8 (35) 1 (36) |
| Характеристики | Выпуклый, дельтаэдр |
| Сеть |  |
В геометрия, икосаэдр со сжатыми ребрами это многогранник с 18 треугольных лица, 27 ребер и 11 вершин с C2v симметрия, заказ 4.
Строительство
Его можно построить из обычного икосаэдр, с одним сжатие края, удаляя одну вершину, 3 ребра и 2 грани. Это сокращение искажает ограниченная сфера исходные вершины. Со всем равносторонний треугольник граней, он имеет 2 набора по 3 компланарных равносторонних треугольника (каждый из которых образует полу-шестиугольник), и поэтому не является Джонсон солид.
Если наборы из трех копланарных треугольников считаются одной гранью (называемой триамонд[1]), у него 10 вершин, 22 ребра и 14 граней, 12 треугольников. ![]() и 2 бриллианта
и 2 бриллианта ![]() .
.
Его также можно описать как гибрид квадрат-пятиугольник антипризматический сердечник (антипризматический сердечник с одним квадратным основанием и одним пятиугольным основанием); каждая база тогда дополненный с пирамида.
Связанные многогранники
В правильный икосаэдр в разрезе вариант, топологически эквивалентный сфенокорона с двумя наборами из 3 копланарных граней в виде трапеций. Это вершина фигуры 4D многогранник, великая антипризма. Он имеет 10 вершин, 22 ребра, 12 равносторонних треугольных граней и 2 грани трапеции.[2]
В химии
В химия, этот многогранник чаще всего называют октадекаэдр, для 18 треугольных граней и представляет собой близко-boranate [B11ЧАС11]2−. [3]
 близко-boranate [B11ЧАС11]2− |  Сеть |
Связанные многогранники
В удлиненный октаэдр похож на икосаэдр со сжатыми ребрами, но вместо сжатия только одного ребра стягиваются два противоположных ребра.
Рекомендации
- ^ http://www.interocitors.com/polyhedra/Triamonds/
- ^ Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26) Великая Антипризма
- ^ Холлеман, Арнольд Фредерик; Виберг, Эгон (2001), Виберг, Нильс (ред.), Неорганическая химия, переведенный Иглсоном, Мэри; Брюэр, Уильям, Сан-Диего / Берлин: Academic Press / De Gruyter, p. 1165, г. ISBN 0-12-352651-5
