WikiDer > Уравнение времени
В уравнение времени описывает несоответствие между двумя видами солнечное время. Слово уравнение используется в средневековом смысле «примирить различие». Два раза отличаются кажущееся солнечное время, который напрямую отслеживает дневное движение из солнце, и среднее солнечное время, который отслеживает теоретический иметь в виду Солнце с равномерным движением. Кажущееся солнечное время может быть получено путем измерения текущего положения (часовой угол) Солнца, на что указывает (с ограниченной точностью) солнечные часы. Иметь в виду солнечное время для одного и того же места будет временем, указанным устойчивыми часами, установленными так, чтобы в течение года его отличия от видимого солнечного времени имели бы среднее значение ноль.[1]
Уравнение времени - это восточная или западная составляющая аналемма, кривая, представляющая угловое смещение Солнца от его среднего положения на небесная сфера если смотреть с Земли. Уравнение значений времени для каждого дня года, составленное астрономической обсерватории, были широко перечислены в альманахи и эфемериды.[2][3]:14
Концепция

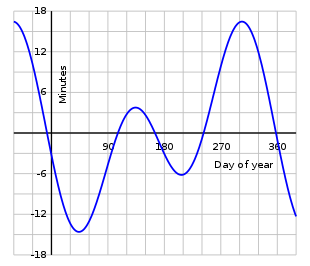
В течение года уравнение времени меняется, как показано на графике; его изменение от года к году невелико. Видимое время и солнечные часы могут опережать (быстрее) на целых 16мин 33 s (примерно 3 ноября) или отстает (медленно) на целых 14 минут 6 секунд (примерно 11 февраля). Уравнение времени имеет нули около 15 апреля, 13 июня, 1 сентября и 25 декабря. Если не учитывать очень медленные изменения орбиты и вращения Земли, эти события повторяются каждый раз в одно и то же время. тропический год. Однако из-за нецелого количества дней в году эти даты могут меняться на день или около того из года в год.[n 1][4]:277
График уравнения времени очень хорошо аппроксимируется суммой двух синусоид, одна с периодом в год, а другая с периодом в полгода. Кривые отражают два астрономических эффекта, каждый из которых вызывает различную неоднородность в видимом суточном движении Солнца относительно звезд:
- в наклонность из эклиптика (плоскость годового орбитального движения Земли вокруг Солнца), которая наклонена примерно на 23,44 градуса относительно плоскости Земли экватор; и
- в эксцентриситет из Орбита Земли вокруг Солнца, что составляет около 0,0167.
Уравнение времени есть постоянный только для планеты с нулем осевой наклон и ноль орбитальный эксцентриситет. На Марс разница между временем на солнечных часах и часами может достигать 50 минут из-за значительно большего эксцентриситета его орбиты. Планета Уран, который имеет чрезвычайно большой наклон оси, имеет уравнение времени, в соответствии с которым его дни начинаются и заканчиваются на несколько часов раньше или позже, в зависимости от того, где он находится на своей орбите.
Знак уравнения времени
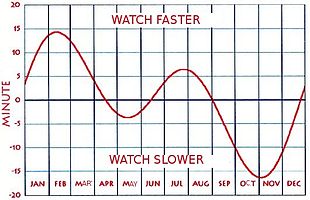
Военно-морская обсерватория США заявляет: «Уравнение времени - это разница. кажущееся солнечное время минус среднее солнечное время", т.е. если солнце опережает часы, знак положительный, а если часы опережают солнце, знак отрицательный.[5][6] Уравнение времени показано на верхнем графике выше для периода чуть более года. Нижний график (который охватывает ровно один календарный год) имеет те же абсолютные значения, но знак перевернут, поскольку он показывает, насколько часы опережают солнце. Публикации могут использовать любой формат - в англоязычном мире более распространено первое использование, но не всегда. Любой, кто использует опубликованную таблицу или график, должен сначала проверить использование их знаков. Часто это объясняется примечанием или подписью. В противном случае использование может быть определено, зная, что в течение первых трех месяцев каждого года часы опережают солнечные часы. В мнемонический «NYSS» (произносится как «хороший»), что означает «новый год, медленные солнечные часы», может быть полезным. Некоторые опубликованные таблицы избегают двусмысленности, не используя знаки, а показывая вместо них такие фразы, как «солнечные часы быстро» или «солнечные часы медленно».[7]
В этой и других статьях английской Википедии положительное значение уравнения времени означает, что солнечные часы опережают часы.
История
Фраза «уравнение времени» происходит от средневековая латынь aequātiō diērum, что означает «уравнение дней» или «разница дней». Слово aequātiō (и Средний английский уравнение) использовался в средневековой астрономии для табулирования разницы между наблюдаемым значением и ожидаемым значением (как в уравнении центра, уравнении равноденствий, уравнении эпицикла). Джеральд Дж. Тумер использует средневековый термин «уравнение» от латинского aequātiō[n 2], для разницы Птолемея между средним солнечным временем и видимым солнечным временем. Иоганн КеплерОпределение уравнения - это «разница между количеством градусов и минут средней аномалии и градусами и минутами исправленной аномалии».[8]:155
Разница между видимым солнечным временем и средним временем была признана астрономами с древних времен, но до изобретения точных механических часов в середине 17 века, солнечные часы были единственными надежными часами, и общепринятым стандартом было кажущееся солнечное время. Среднее время не вытесняло очевидное время в национальных альманахах и эфемеридах до начала 19 века. [9]
Ранняя астрономия
Неравномерное ежедневное движение Солнца было известно вавилонянам.[нужна цитата]
Книга III из Птолемейс Альмагест (2-й век) в первую очередь занимается аномалией Солнца, и он представил уравнение времени в своей таблице. Удобные столы.[10] Птолемей обсуждает поправку, необходимую для преобразования пересечения Солнца по меридиану в среднее солнечное время, и принимает во внимание неоднородное движение Солнца по эклиптике и поправку на меридиан для эклиптической долготы Солнца. Он заявляет, что максимальная поправка8 1⁄3 время-градусы или5⁄9 часа (Книга III, глава 9).[11] Однако он не считал этот эффект актуальным для большинства расчетов, так как он был незначительным для медленно движущихся светил и применил его только к самому быстро движущемуся светилу - Луне.
Основываясь на обсуждении Птолемея в Альмагест, значения для уравнения времени (арабский тахдил аль-айям би лайалайха) были стандартными для столов (zij) в произведениях средневековая исламская астрономия.[12]
Ранний современный период
Описание кажущегося и среднего времени было дано Невил Маскелайн в Морской Альманах для 1767 года: «Кажущееся время - это время, которое выводится непосредственно из Солнца, будь то наблюдение прохождения им меридиана или наблюдение за ним. Рост или же Параметр. Это время отличается от времени, которое показывают часы и часы, хорошо отрегулированные на Земле, которое называется приравненным или средним временем ». Далее он сказал, что в море кажущееся время, найденное при наблюдении за Солнцем, должно быть скорректировано уравнением времени, если наблюдателю требуется среднее время.[1]
Первоначально правильным временем считалось то, которое показывают солнечные часы. Когда были представлены хорошие механические часы, они согласовывались с солнечными часами только около четырех дат каждый год, поэтому уравнение времени использовалось, чтобы «скорректировать» их показания, чтобы получить солнечные часы. Некоторые часы, называемые часы с уравнениями, включал внутренний механизм для выполнения этой «коррекции». Позже, когда часы стали доминирующими в хороших часах, некорректированное время, то есть «среднее время», стало общепринятым стандартом. Показания солнечных часов, когда они использовались, тогда корректировались и часто все еще корректируются с помощью уравнения времени, которое использовалось в обратном направлении по сравнению с предыдущим, чтобы получить время на часах. Поэтому на многих солнечных часах выгравированы таблицы или графики уравнения времени, позволяющие пользователю внести эту поправку.[нужна цитата]
Уравнение времени исторически использовалось для установить часы. Между изобретением точных часов в 1656 году и появлением коммерческих служб распределения времени около 1900 года существовало три распространенных наземных способа установки часов. Во-первых, в необычном случае присутствия астронома прохождение Солнца через меридиан (момент, когда солнце прошло над головой) было отмечено, часы были установлены на полдень и смещены на количество минут, заданное уравнением времени для этой даты. Во-вторых, что гораздо чаще, считывали солнечные часы, сверялись с таблицей уравнения времени (обычно выгравированной на циферблате) и устанавливали часы или часы соответственно. Они рассчитали среднее время, хотя и локальное для точки долгота. Третий метод не использовал уравнение времени; вместо этого он использовал звездный наблюдения, чтобы дать звездное время, используя взаимосвязь между звездным временем и среднее солнечное время.[13]:57–58
Первые таблицы, которые дают уравнение времени по существу правильно, были опубликованы в 1665 г. Кристиан Гюйгенс.[14] Гюйгенс, следуя традиции Птолемея и средневековых астрономов в целом, установил свои значения для уравнения времени так, чтобы все значения были положительными в течение года.[14][n 3]
Другой набор таблиц был опубликован в 1672–1673 гг. Джон Флемстид, который впоследствии стал первым Королевский астроном нового Королевская Гринвичская обсерватория. Похоже, это были первые по существу правильные таблицы, которые давали сегодняшнее значение среднего времени (ранее, как отмечалось выше, знак уравнения всегда был положительным, и он устанавливался на ноль, когда кажущееся время восхода солнца было самым ранним относительно часов. время восхода солнца). Флемстид принял соглашение о табулировании и названии поправки в том смысле, что она должна применяться к кажущемуся времени для получения среднего времени.[15]
Уравнение времени, правильно основанное на двух основных компонентах неравномерности видимого движения Солнца,[n 4] не получил широкого распространения до тех пор, пока не были опубликованы таблицы Флэмстида 1672–1673 годов вместе с посмертным изданием работ Джеремайя Хоррокс.[16]:49
Роберт Гук (1635–1703), которые математически проанализировали универсальный шарнир, был первым, кто заметил, что геометрия и математическое описание (несекулярного) уравнения времени и универсального шарнира идентичны, и предложил использовать универсальный шарнир в конструкции «механических солнечных часов».[17]:219
18 и начало 19 веков
Поправки в таблицах Флемстида 1672–1673 и 1680 гг. Дали среднее время, вычисленное по существу правильно и без необходимости дальнейшего смещения. Но числовые значения в таблицах уравнения времени с тех пор несколько изменились из-за трех факторов:
- общее повышение точности, которое произошло благодаря усовершенствованию методов астрономических измерений,
- медленные внутренние изменения в уравнении времени, происходящие в результате небольших долгосрочных изменений угла наклона и эксцентриситета Земли (влияющих, например, на расстояние и даты перигелий), и
- включение небольших источников дополнительных изменений в видимом движении Солнца, неизвестных в 17 веке, но обнаруженных с 18 века и далее, включая эффекты Луны[n 5], Венера и Юпитер.[18]

С 1767 по 1833 год британцы Морской альманах и астрономические эфемериды табулировал уравнение времени в смысле «прибавить или вычесть (как указано) количество минут и секунд, указанных в или из кажущегося времени, чтобы получить среднее время». Время в альманахе соответствует солнечному времени, поскольку время на борту корабля чаще всего определяется по Солнцу. Эта операция будет выполнена в том необычном случае, когда потребуется среднее солнечное время наблюдения. В выпусках с 1834 года всегда использовалось среднее солнечное время, потому что к тому времени время на борту корабля все чаще определялось морские хронометры. Следовательно, инструкции заключались в том, чтобы прибавить или вычесть (как указано) количество минут, указанное к среднему времени или из него, чтобы получить кажущееся время. Итак, сложение соответствовало положительному положению уравнения, а вычитание отрицательному результату.
Поскольку видимое суточное движение Солнца составляет один оборот в день, то есть на 360 ° каждые 24 часа, а само Солнце появляется в небе в виде диска около 0,5 °, простые солнечные часы могут быть прочитаны с максимальной точностью около одного минута. Поскольку уравнение времени имеет диапазон около 33 минут, разницу между временем на солнечных часах и часами нельзя игнорировать. В дополнение к уравнению времени, нужно также применить поправки из-за своего расстояния от меридиана местного часового пояса и летнее время, если есть.
Крошечное увеличение среднего солнечного дня из-за замедления вращения Земли примерно на 2 РС в день за столетие, который в настоящее время накапливается примерно до 1 секунды каждый год, не принимается во внимание в традиционных определениях уравнения времени, так как это незаметно на уровне точности солнечных часов.
Основные компоненты уравнения
Эта секция возможно содержит оригинальные исследования. (Январь 2018) (Узнайте, как и когда удалить этот шаблон сообщения) |
Эксцентриситет земной орбиты

Земля вращается вокруг Солнца. Если смотреть с Земли, кажется, что Солнце совершает один оборот вокруг Земли через фоновые звезды за один год. Если бы Земля вращалась вокруг Солнца с постоянной скоростью по круговой орбите в плоскости, перпендикулярной оси Земли, то Солнце было бы достигать высшей точки каждый день в одно и то же время и быть идеальным хранителем времени (за исключением очень небольшого эффекта замедления вращения Земли). Но орбита Земли представляет собой эллипс, не центрированный вокруг Солнца, и его скорость варьируется от 30,287 до 29,291 км / с, согласно данным Законы движения планет Кеплера, и его угловая скорость также меняется, и поэтому кажется, что Солнце движется быстрее (относительно звезд фона) на перигелий (в настоящее время около 3 января) и медленнее на афелий пол года спустя. [19][неудачная проверка]
В этих крайних точках этот эффект изменяет видимые солнечные сутки на 7,9 с / день от их среднего значения. Следовательно, меньшие суточные различия в скорости в другие дни накапливаются до этих точек, отражая, как планета ускоряется и замедляется по сравнению со средним значением. В результате эксцентриситет орбиты Земли вносит периодическое изменение, которое (в первом приближении) составляет синусоидальная волна с амплитудой 7,66 мин и период одного года к уравнению времени. Нулевые точки достигаются в перигелии (начало января) и афелии (начало июля); экстремальные значения приходятся на начало апреля (отрицательное) и начало октября (положительное).
Наклон эклиптики
Даже если бы орбита Земли была круговой, воспринимаемое движение Солнца по нашей небесный экватор все равно не будет униформой. Это следствие наклона оси вращения Земли по отношению к плоскость его орбиты, или, что то же самое, наклон эклиптика (путь, по которому, кажется, идет Солнце в небесная сфера) с уважением к небесный экватор. Проекция этого движения на нашу небесный экватор, по которым отсчитывается «время часов», является максимумом на солнцестояния, когда годовое движение Солнца параллельно экватору (вызывая усиление воспринимаемой скорости) и приводит в основном к изменению прямое восхождение. Это минимум на равноденствия, когда видимое движение Солнца более наклонное и дает большее изменение склонение, оставляя меньше для компонента в прямое восхождение, который является единственным компонентом, влияющим на продолжительность солнечных суток. Практической иллюстрацией наклона является то, что суточный сдвиг тени, отбрасываемой Солнцем на солнечные часы даже на экваторе, меньше ближе к солнцестоянию и больше ближе к равноденствиям. Если бы этот эффект работал сам по себе, то дни были бы до 24 часов 20,3 секунды (измеренные с солнечного полудня до солнечного полудня) около солнцестояний и на 20,3 секунды короче, чем 24 часа около равноденствий.[20][неудачная проверка]
На рисунке справа мы можем видеть месячный ход видимого наклона плоскости эклиптики в солнечный полдень, если смотреть с Земли. Это изменение связано с очевидным прецессия вращения Земли в течение года, если смотреть с Солнца в солнечный полдень.
В терминах уравнения времени наклон эклиптики приводит к вкладу вариации синусоидальной волны с амплитудой 9,87 минут и периодом в полгода в уравнение времени. Нулевые точки этой синусоидальной волны достигаются в дни равноденствий и солнцестояний, в то время как экстремумы приходятся на начало февраля и августа (отрицательные) и начало мая и ноября (положительные).
Светские эффекты
Два вышеупомянутых фактора имеют разные длины волн, амплитуды и фазы, поэтому их совокупный вклад представляет собой нерегулярную волну. В эпоха 2000 это значения (в минутах и секундах с UT даты):
| Точка | Ценить | Дата |
|---|---|---|
| минимум | −14 мин 15 с | 11 февраля |
| нуль | 0 мин0 с | 15 апреля |
| максимум | +3 мин 41 с | 14 мая |
| нуль | 0 мин0 с | 13 июн |
| минимум | −6 мин 30 с | 26 июля |
| нуль | 0 мин0 с | 1 сентября |
| максимум | +16 мин 25 с | 3 ноября |
| нуль | 0 мин0 с | 25 декабря |
- E.T. = кажущийся - средний. Положительный результат означает: солнце бежит быстро и достигает своей кульминации раньше, или солнечные часы опережают среднее время. Небольшие годовые колебания возникают из-за наличия високосных лет, которые сбрасываются каждые 4 года. Точная форма уравнения временной кривой и связанная с ней аналемма медленно меняются на протяжении веков из-за светские вариации как в эксцентриситете, так и в наклонности. В настоящий момент оба показателя медленно уменьшаются, но они увеличиваются и уменьшаются в течение сотен тысяч лет.[21]
В более коротких временных масштабах (тысячи лет) сдвиги в датах равноденствия и перигелия будут более важными. Первое вызвано прецессия, и сдвигает точку равноденствия назад по сравнению со звездами. Но в текущем обсуждении его можно проигнорировать, поскольку Григорианский календарь построена таким образом, чтобы сохранить дату весеннего равноденствия на 20 марта (по крайней мере, с достаточной точностью для нашей цели здесь). Перигелий сдвигается вперед, примерно на 1,7 дня в столетие. В 1246 году перигелий произошел 22 декабря, в день солнцестояния, поэтому две составляющие волны имели общие нулевые точки, а уравнение кривой времени было симметричным: Астрономические алгоритмы Meeus дает экстремумы в феврале и ноябре в 15 м 39 с, а в мае и июле - в 4 м 58 с. До этого февральский минимум был больше ноябрьского максимума, а майский максимум - июльский. Фактически, в годы до -1900 (1901 г. до н.э.) майский максимум был больше, чем ноябрьский максимум. В году –2000 (2001 г. до н.э.) максимум в мае составлял +12 минут и пара секунд, а максимум в ноябре был чуть меньше 10 минут. Секулярное изменение становится очевидным, если сравнить текущий график уравнения времени (см. Ниже) с графиком 2000-летней давности, например, построенным на основе данных Птолемея.[22]
Графическое представление

Практическое использование
Если гномон (отбрасывающий тень объект) - это не край, а точка (например, отверстие в пластине), тень (или пятно света) будет очерчивать кривую в течение дня. Если тень отбрасывается на плоскую поверхность, эта кривая будет коническая секция (обычно гипербола), так как круг движения Солнца вместе с точкой гномона определяют конус. В период весеннего и осеннего равноденствий конус вырождается в плоскость, а гипербола - в линию. С другой гиперболой для каждого дня, на каждую гиперболу можно поставить часовые отметки, которые включают любые необходимые исправления. К сожалению, каждая гипербола соответствует двум разным дням, по одному в каждой половине года, и эти два дня потребуют разных корректировок. Удобный компромисс - провести линию для «среднего времени» и добавить кривую, показывающую точное положение теневых точек в полдень в течение года. Эта кривая примет форму восьмерки и известна как аналемма. Сравнивая аналемму со средней полуденной линией, можно определить величину поправки, которая обычно применяется в этот день.
Уравнение времени используется не только в связи с солнечные часы и подобных устройств, но также для многих приложений солнечная энергия. Такие машины как солнечные трекеры и гелиостаты должны двигаться в соответствии с уравнением времени.
Гражданское время это местное среднее время для меридиана, который часто проходит около центра часовой пояс, и может быть дополнительно изменен летнее время. Когда необходимо найти кажущееся солнечное время, которое соответствует данному гражданскому времени, необходимо учитывать разницу в долготе между интересующим местом и меридианом часового пояса, летнее время и уравнение времени.[23]
Расчет уравнения времени
Уравнение времени получается из опубликованной таблицы или графика. Для дат в прошлом такие таблицы составляются на основе исторических измерений или расчетов; для будущих дат, конечно, можно только рассчитать таблицы. В таких устройствах, как гелиостаты с компьютерным управлением, компьютер часто запрограммирован на вычисление уравнения времени. Расчет может быть числовым или аналитическим. Первые основаны на численное интегрирование дифференциальных уравнений движения, включая все существенные гравитационные и релятивистские эффекты. Результаты имеют точность лучше 1 секунды и являются основой для данных современного альманаха. Последние основаны на решении, которое включает только гравитационное взаимодействие между Солнцем и Землей, проще, но не так точно, как первое. Его точность можно улучшить, добавив небольшие поправки.
Следующее обсуждение описывает достаточно точный (согласование с данными Альманаха с точностью до 3 секунд в широком диапазоне лет) алгоритм уравнения времени, который хорошо известен астрономам.[24]:89 В нем также показано, как получить простую приближенную формулу (с точностью до 1 минуты в течение большого интервала времени), которую можно легко вычислить с помощью калькулятора, и дано простое объяснение явления, которое использовалось ранее в этой статье.
Математическое описание
Точное определение уравнения времени:[25]:1529
- EOT = GHA - GMHA
Величины, входящие в это уравнение, следующие:
- EOT, разница во времени между кажущееся солнечное время и среднее солнечное время;
- ГСГ, Гринвич Часовой угол видимого (действительного) Солнца;
- GMHA = универсальное время - смещение, средний часовой угол по Гринвичу среднего (фиктивного) Солнца.
Здесь время и угол - это величины, которые связаны такими факторами, как: 2π радианы = 360 ° = 1 день = 24 часа. Разницу, EOT, можно измерить, поскольку GHA - это угол, который можно измерить и Всемирное время, UT - шкала для измерения времени. Смещение на π = 180 ° = 12 часов от UT необходимо, потому что UT равно нулю в среднюю полночь, а GMHA = 0 в средний полдень.[n 6] И ГСГ, и ГСГ, как и все физические углы, имеют математический, но не физический разрыв в их соответствующем (кажущемся и среднем) полдень. Несмотря на математические разрывы его компонентов, EOT определяется как непрерывная функция путем добавления (или вычитания) 24 часов в небольшой интервал времени между разрывами в GHA и GMHA.
Согласно определениям углов на небесной сфере ГСГ = ГАСТ - α (видеть часовой угол)
куда:
- GAST - это очевидный гринвичский звездное время (угол между кажущимся весеннее равноденствие и меридиан в плоскости экватора). Это известная функция UT.[26]
- α это прямое восхождение видимого Солнца (угол между кажущимся весенним равноденствием и фактическим Солнцем в плоскости экватора).
При подстановке в уравнение времени это
- EOT = GAST - α - UT + смещение
Подобно формуле для ГСГ выше, можно написать GMHA = ГАСТ - αM, где последний член - прямое восхождение среднего Солнца. Уравнение часто записывается в этих терминах как[4]:275[27]:45
- EOT = αM − α
куда αM = GAST - UT + смещение. В этой формулировке измерение или вычисление EOT для определенного значения времени зависит от измерения или вычисления α в это время. Обе α и αM варьируются от 0 до 24 часов в течение года. В первом случае наблюдается разрыв во время, зависящее от значения UT, а во втором - несколько позже. Как следствие, при таком расчете EOT имеет два искусственных разрыва. Оба они могут быть удалены путем вычитания 24 часов из значения EOT в небольшом интервале времени после разрыва в α и перед тем в αM. Результирующий EOT является непрерывной функцией времени.
Другое определение, обозначенное E чтобы отличить его от EOT, это
- E = GMST - α - UT + смещение
Здесь GMST = GAST - eqeq, - среднее звездное время по Гринвичу (угол между средним весенним равноденствием и средним Солнцем в плоскости экватора). Следовательно, GMST является приближением к GAST (и E является приближением к EOT); eqeq называется уравнением равноденствий и возникает из-за колебаний, или нутация оси вращения Земли вокруг ее прецессионного движения. Поскольку амплитуда нутационного движения составляет всего около 1,2 с (18 ″ долготы), разница между EOT и E можно игнорировать, если никто не интересуется точностью до секунды.
Третье определение, обозначенное Δт чтобы отличить его от EOT и E, и теперь называется уравнением эфемеридного времени[25]:1532 (до различия, которое теперь проводится между EOT, E, и Δт последнее было известно как уравнение времени)
- Δт = Λ − α
здесь Λ это эклиптическая долгота среднего Солнца (угол от среднего весеннего равноденствия до среднего Солнца в плоскости эклиптика).
Разница Λ - (GMST - UT + смещение) составляет 1,3 с с 1960 по 2040 год. Следовательно, в этом ограниченном диапазоне лет Δт - аппроксимация EOT, ошибка которой находится в диапазоне от 0,1 до 2,5 с в зависимости от поправки на долготу в уравнении равноденствий; для многих целей, например для корректировки солнечных часов, этой точности более чем достаточно.
Расчет прямого восхождения
Прямое восхождение и, следовательно, уравнение времени могут быть вычислены с помощью теории двух тел Ньютона небесного движения, в которой тела (Земля и Солнце) описывают эллиптические орбиты вокруг своего общего центра масс. Используя эту теорию, уравнение времени становится
- Δт = M + λп − α
где появляются новые углы
- M = 2π (т − тп)/тY, это средняя аномалия, угол от перицентр эллиптической орбиты к среднему Солнцу; его диапазон от 0 до 2π в качестве т увеличивается с тп к тп + тY;
- тY = 365.2596358 дней - это продолжительность аномальный год: интервал времени между двумя последовательными проходами перицентра;
- λп = Λ − M, - эклиптическая долгота перицентра;
- т является динамическое время, независимая переменная в теории. Здесь оно считается идентичным непрерывному времени, основанному на UT (см. Выше), но в более точных расчетах ( E или EOT) необходимо учитывать небольшую разницу между ними.[25]:1530[26] а также различие между UT1 и UTC.
- тп это ценность т в перицентрическом отделе.
Для завершения расчета требуются три дополнительных угла:
- E, Солнце эксцентрическая аномалия (обратите внимание, что это отличается от M);
- ν, Солнце истинная аномалия;
- λ = ν + λп, истинная долгота Солнца на эклиптике.
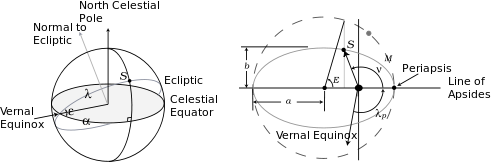
Все эти углы показаны на рисунке справа, который показывает небесная сфера и Солнце эллиптическая орбита видимый с Земли (такой же, как орбита Земли, видимая со стороны Солнца). На этом рисунке ε это наклонность, пока е = √1 − (б/а)2 это эксцентриситет эллипса.
Теперь с учетом значения 0 ≤ M ≤ 2π, можно вычислить α(M) с помощью следующей известной процедуры:[24]:89
Во-первых, учитывая Mрассчитать E из Уравнение Кеплера:[28]:159
- M = E − е грех E
Хотя это уравнение не может быть решено точно в замкнутой форме, значения E(M) могут быть получены с помощью бесконечных (степенных или тригонометрических) рядов, графических или численных методов. В качестве альтернативы обратите внимание, что для е = 0, E = M, и по итерации:[29]:2
- E ≈ M + е грех M.
Это приближение можно улучшить при малых е, повторяя снова,
- E ≈ M + е грех M + 1/2е2 грех 2M,
и продолжающаяся итерация дает последовательно более высокие члены разложения степенного ряда по е. Для малых значений е (намного меньше 1) два или три члена ряда дают хорошее приближение для E; меньший е, тем лучше приближение.
Далее, зная Eвычислить истинная аномалия ν из отношения эллиптической орбиты[28]:165
Правильная ветвь многозначной функции загар−1 Икс использовать тот, который делает ν непрерывная функция E(M) начиная с νE=0 = 0. Таким образом, для 0 ≤ E <π использовать загар−1 Икс = Загар−1 Икс, и для π < E ≤ 2π использовать загар−1 Икс = Загар−1 Икс + π. При определенной стоимости E = π для чего аргумент загар бесконечно, используйте ν = E. Здесь Загар−1 Икс главная ветвь, |Загар−1 Икс| < π/2; функция, возвращаемая калькуляторами и компьютерными приложениями. В качестве альтернативы, эту функцию можно выразить через ее Серия Тейлор в е, первые три члена из которых:
- ν ≈ E + е грех E + 1/4е2 грех 2E.
Для малых е это приближение (или даже только первые два члена) хорошее. Комбинируя приближение для E(M) с этим для ν(E) производит
- ν ≈ M + 2е грех M + 5/4е2 грех 2M.
Соотношение ν(M) называется уравнение центра; записанное здесь выражение представляет собой приближение второго порядка по е. При небольшом значении е который характеризует орбиту Земли, это дает очень хорошее приближение для ν(M).
Далее, зная νрассчитать λ из его определения:
- λ = ν + λп
Значение λ изменяется нелинейно с M потому что орбита эллиптическая, а не круглая. Из приближения для ν:
- λ ≈ M + λп + 2е грех M + 5/4е2 грех 2M.
Наконец, зная λ вычислить α из отношения для прямоугольного треугольника на небесной сфере, показанного выше[30]:22
- α = загар−1(потому что ε загар λ)
Обратите внимание, что квадрант α такой же, как у λ, поэтому уменьшить λ в диапазоне от 0 до 2π и писать
- α = Загар−1 (потому что ε загар λ) + kπ,
куда k равно 0, если λ находится в квадранте 1, это 1, если λ находится в квадрантах 2 или 3, и это 2, если λ находится в квадранте 4. Для значений, при которых tan бесконечен, α = λ.
Хотя приблизительные значения для α можно получить из усеченных рядов Тейлора, подобных ν,[31]:32 более эффективно использовать уравнение[32]:374
- α = λ - грех−1 [у грех (α + λ)]
куда у = загар2(ε/2). Обратите внимание, что для ε = у = 0, α = λ и повторяется дважды:
- α ≈ λ − у грех 2λ + 1/2у2 грех 4λ.
Уравнение времени
Уравнение времени получается путем подстановки результата вычисления прямого восхождения в формулу уравнения времени. Здесь Δт(M) = M + λп − α[λ(M)] используется; частично из-за небольших исправлений (порядка 1 секунды), которые оправдали бы использование E, не включены, и отчасти потому, что цель состоит в том, чтобы получить простое аналитическое выражение. Используя двухчленные приближения для λ(M) и α(λ), позволяет Δт быть записанным как явное выражение двух терминов, которые обозначаются Δтэй потому что это приближение первого порядка по е И в у.
- Δтэй = −2е грех M + y sin (2M + 2λп) = −7,659 грех M + 9,863 греха (2M + 3.5932) минут
Это уравнение было впервые выведено Милном,[32]:375 кто написал это в терминах λ = M + λп. Записанные здесь числовые значения являются результатом использования значений орбитальных параметров, е = 0.016709, ε = 23.4393° = 0.409093 радианы и λп = 282.9381° = 4.938201 радианы, соответствующие эпохе 1 января 2000 года в 12 часов дня UT1. При вычислении числового выражения для Δтэй как указано выше, для получения правильных значений калькулятор должен быть в радианах, поскольку значение 2λп - 2π в аргументе второго члена написано там в радианах. Также можно записать приближения более высокого порядка:[33]:Уравнения (45) и (46) но у них обязательно больше терминов. Например, приближение второго порядка в обоих е и у состоит из пяти сроков[25]:1535
- Δте2у2 = Δтэй − 5/4е2 грех 2M + эй грех M cos (2M + 2λп) − 1/2у2 грех (4M + 4λп)
Это приближение имеет потенциал для высокой точности, однако, чтобы достичь ее в течение широкого диапазона лет, параметры е, ε, и λп должно изменяться со временем.[24]:86[25]:1531,1535 Это создает дополнительные вычислительные сложности. Были предложены другие приближения, например, Δте[24]:86[34] который использует уравнение первого порядка для центра, но не использует другое приближение для определения α, и Δте2[35] в котором используется уравнение второго порядка для центра.
Временная переменная, M, можно записать либо в терминах п, количество дней после перигелия, или D, количество дней после определенной даты и времени (эпохи):
- M = 2π/тYп дней = MD + 2π/тYD дней = 6.24004077 + 0.01720197D
Здесь MD это ценность M в выбранную дату и время. Для приведенных здесь значений в радианах MD - это то, что измерено для фактического Солнца в эпоху 1 января 2000 года в 12 полдня UT1, и D количество дней, прошедших с той эпохи. В периапсисе M = 2π, поэтому решение дает D = Dп = 2.508109. Это помещает перицентр 4 января 2000 года в 00:11:41, в то время как фактический перицентр, согласно результатам Многолетний интерактивный компьютерный альманах[36] (сокращенно MICA) 3 января 2000 г. в 05:17:30. Это большое несоответствие происходит из-за того, что разница между радиусами орбиты в двух местах составляет всего 1 часть на миллион; другими словами, радиус - очень слабая функция времени около перицентра. На практике это означает, что нельзя получить высокоточный результат для уравнения времени, используя п и добавление фактической даты периапсиса для данного года. Однако высокой точности можно добиться, используя формулировку с точки зрения D.
Когда D > Dп, M больше 2π и нужно вычесть кратное 2π (это зависит от года) от него, чтобы привести его в диапазон от 0 до 2π. Точно так же для лет до 2000 года нужно складывать числа, кратные 2π. Например, за 2010 год D варьируется от 3653 1 января с полудня до 4017 31 декабря в полдень соответствующий M ценности 69.0789468 и 75.3404748 и уменьшаются до диапазона от 0 до 2π путем вычитания 10 и 11 умножить на 2π соответственно. Всегда можно написать D = пY + d, куда пY - количество дней от эпохи до полудня 1 января желаемого года, и 0 ≤ d ≤ 364 (365, если расчет для високосного года).
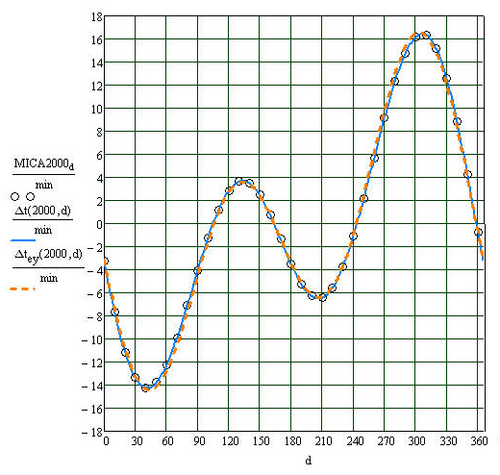
Результат вычислений обычно представлен либо в виде набора табличных значений, либо в виде графика уравнения времени как функции d. Сравнение участков Δт, Δтэй, а результаты MICA за 2000 год показаны на рисунке справа. Сюжет о Δтэй близка к результатам MICA, абсолютная ошибка, Err = |Δтэй - MICA2000|, менее 1 минуты в течение года; его наибольшее значение составляет 43,2 секунды и приходится на 276 день (3 октября). Сюжет о Δт неотличим от результатов MICA, наибольшая абсолютная ошибка между ними составляет 2,46 с на 324-й день (20 ноября).
Замечание о непрерывности уравнения времени
Для выбора подходящей ветки арктан В отношении непрерывности функции полезна модифицированная версия функции арктангенса. Он приносит предыдущие знания об ожидаемом значении параметра. Модифицированная функция арктангенса определяется как:
- арктанη Икс = arctan Икс + π раунд (η - арктан Икс/π).
Он дает значение, максимально близкое к η насколько возможно. Функция круглый округляет до ближайшего целого числа.
Применение этого дает:
- Δт(M) = M + λп - арктан(M+λп) (потому что ε загар λ).
Параметр M + λп организует здесь, чтобы установить Δт до ближайшего к нулю значения, которое является искомым.
Светские эффекты
Разница между MICA и Δт результаты проверялись каждые 5 лет в диапазоне с 1960 по 2040 год. В каждом случае максимальная абсолютная ошибка составляла менее 3 с; самая большая разница, 2,91 с, произошла 22 мая 1965 г. (141 день). Однако для достижения такого уровня точности в этом диапазоне лет необходимо учитывать вековые изменения параметров орбиты со временем. Уравнения, описывающие это изменение:[24]:86[25]:1531,1535
Согласно этим соотношениям, через 100 лет (D = 36525), λп увеличивается примерно на 0,5% (1,7 °), е уменьшается примерно на 0,25%, а ε уменьшается примерно на 0,05%.
В результате количество вычислений, требуемых для любого из приближений высшего порядка уравнения времени, требует, чтобы компьютер выполнял их, если кто-то хочет достичь присущей им точности в широком диапазоне времени. В этом случае оценить не сложнее. Δт используя компьютер, чем любое из его приближений.
Во всем этом обратите внимание, что Δтэй как написано выше, легко оценить, даже с помощью калькулятора, достаточно точен (лучше, чем 1 минута за 80-летний диапазон) для корректировки солнечных часов и имеет приятное физическое объяснение как сумму двух членов, одно из которых связано с наклонным углом и другой - эксцентриситет, который использовался ранее в статье. Это неверно и для Δт рассматривается как функция M или для любого из его приближений более высокого порядка.
Альтернативный расчет
Другой расчет уравнения времени можно сделать следующим образом.[34] Углы указаны в градусах; обычный порядок действий применяется.
- W = 360°/365,24 дня
W - средняя угловая орбитальная скорость Земли в градусах в сутки.
- А = W × (D + 10)
D - дата в днях, начинающаяся с нуля 1 января (т. е. часть дней порядковая дата минус 1). 10 - приблизительное количество дней от декабрьского солнцестояния до 1 января. А это угол, на который Земля двигалась бы по своей орбите со средней скоростью с момента декабрьского солнцестояния до настоящего времени. D.
- B = А + 360°/π × 0,0167 × sin [W(D − 2)]
B угол, на который Земля перемещается от точки солнцестояния до настоящего времени D, включая поправку первого порядка на эксцентриситет земной орбиты 0,0167. Цифра 2 - это количество дней с 1 января до даты Земли. перигелий. Это выражение для B можно упростить, объединив константы:
- B = А + 1,914 ° × грех [W(D − 2)].
C представляет собой разницу между углами, перемещаемыми со средней скоростью, и скорректированной скоростью, проецируемыми на экваториальную плоскость, и деленную на 180, чтобы получить разницу в "пол-оборота". Значение 23,44 ° - это наклон (наклон) оси Земли. Вычитание дает условный знак уравнению времени. Для любого заданного значения Икс, арктан Икс (иногда пишется как загар−1 Икс) имеет несколько значений, отличающихся друг от друга целым числом полуворотов. Значение, генерируемое калькулятором или компьютером, может не подходить для этого расчета. Это может вызвать C ошибиться на целое число полуоборотов. Лишние полувороты удаляются на следующем этапе расчета, чтобы получить уравнение времени:
- EOT = 720 × (C - nint (C)) минут
Выражение nint (C) означает ближайшее целое число к C. На компьютере его можно запрограммировать, например, как ИНТ (C + 0,5). Это 0, 1 или 2 в разное время года. После вычитания остается небольшое положительное или отрицательное дробное число полуоборотов, которое умножается на 720, количество минут (12 часов), которое Земля требуется, чтобы повернуться на пол-оборота относительно Солнца, чтобы получить уравнение времени.
По сравнению с опубликованными значениями,[7] этот расчет имеет среднеквадратическое значение погрешность всего 3,7 с. Наибольшая погрешность составляет 6,0 с. Это намного более точное приближение, чем описанное выше, но не такое точное, как сложный расчет.
Приложение о солнечном склонении
Значение B в приведенном выше расчете - это точное значение эклиптической долготы Солнца (сдвинутое на 90 °), поэтому склонение Солнца становится легко доступным:
- Склонение = −arcsin (sin 23,44 ° × cos B)
с точностью до долей градуса.
Смотрите также
Примечания и сноски
- Примечания
- ^ Как пример неточности дат, по данным Военно-морской обсерватории США Многолетний интерактивный компьютерный альманах уравнение времени было нулевым в 02:00 UT1 16 апреля 2011 г.
- ^ выравнивание (регулировка)
- ^ Это означало, что любые часы, установленные на среднее время по таблицам Гюйгенса, постоянно отставали примерно на 15 минут по сравнению с сегодняшним средним временем.
- ^ См. Выше
- ^ Видеть барицентр
- ^ В среднем в полночь универсальное время прерывается, поэтому другое количество дней N, целое число, требуется для формирования непрерывного количества time т: т = N + UT/24 часа дней.
- Сноски
- ^ а б Морской Альманах 1767.
- ^ Милхэм, Уиллис I. (1945). Время и хронометристы. Нью-Йорк: Макмиллан. С. 11–15. ISBN 978-0780800083.
- ^ Британская комиссия по долготе (1794 г.). Морской альманах и астрономические эфемериды за 1803 год. Лондон, Великобритания: К. Бактон.
- ^ а б Хейльброн Дж. Л. 1999 Солнце в церкви, (Кембриджская Массачусетс: издательство Гарвардского университета ISBN 0-674-85433-0)
- ^ Департамент астрономических приложений военно-морской обсерватории США (10 августа 2017 г.). "Уравнение времени". Архивировано из оригинал 20 августа 2019 г.. Получено 4 марта 2020.
- ^ Военно-морская обсерватория США (2018). "Астрономический альманах онлайн! Глоссарий: уравнение времени". Архивировано из оригинал 3 октября 2019 г.. Получено 4 марта 2020.
- ^ а б Во, Альберт Э. (1973). Солнечные часы, их теория и конструкция. Нью-Йорк: Dover Publications. п.205. ISBN 978-0-486-22947-8.
- ^ Кеплер, Йоханнес (1995). Воплощение коперниканской астрономии и гармоний мира. Книги Прометея. ISBN 978-1-57392-036-0.
- ^ Маккарти и Зайдельманн, 2009 г., п. 9.
- ^ Нойгебауэр, Отто (1975), История древней математической астрономии, Нью-Йорк / Гейдельберг / Берлин: Springer-Verlag, стр. 984–986, ISBN 978-0-387-06995-1
- ^ Тумер, Г.Дж. (1998). Альмагест Птолемея. Издательство Принстонского университета. п. 171. ISBN 978-0-691-00260-6.
- ^ E.S. Кеннеди, "Обзор исламских астрономических таблиц", Труды Американского философского общества, 46, Часть 2 (1956), п. 19.
- ^ Олмстед, Деннисон (1866). Компендиум по астрономии. Нью-Йорк: Коллинз и брат.
- ^ а б Гюйгенс, Христиан (1665). Kort Onderwys aengaende het gebruyck der Horologien tot het vinden der Lenghten van Oost en West. Гаага: [издатель неизвестен].
- ^ Флемстид, Джон (1673 г.) [1672 г. для оттиска и переплет с другими печатными частями 1673 г.]. De Inaequalitate Dierum Solarium. Лондон: Уильям Годбид.
- ^ Винс, С. "Полная система астрономии". 2-е издание, том 1, 1814 г.
- ^ Миллс, Аллан (2007). «Карданный шарнир Роберта Гука и его применение к солнечным и солнечным часам». Примечания Рек. Р. Соц. Издательство Королевского общества. 61 (2): 219–236. Дои:10.1098 / RSNR.2006.0172.
- ^ Маскелайн, Невил, "Об уравнении времени и истинном способе его вычисления", Philosophical Transactions, liv (1764), стр. 336 (перепечатано в сокращенном издании, 1809 г., т. 12, стр. 163–169)
- ^ «Эксцентриситет». ffden-2.phys.uaf.edu. Получено 22 января 2018.
- ^ "Наклон". ffden-2.phys.uaf.edu. Получено 22 января 2018.
- ^ Карни, Кевин (декабрь 2005 г.). «Вариация уравнения времени» (PDF).
- ^ Meeus 1997.
- ^ "Как узнать точное время солнечного полудня, где бы вы ни находились."Лондон: Spot-On Sundials. Дата обращения: 23 июля 2013.
- ^ а б c d е Даффет-Смит П. 1988 Практическая астрономия с вашим калькулятором Третье издание (Кембридж: издательство Кембриджского университета).
- ^ а б c d е ж Hughes D.W., Yallop, B.D., & Hohenkerk, C.Y. 1989 г. "Уравнение времени", Ежемесячные уведомления Королевского астрономического общества 238 С. 1529–1535.
- ^ а б "Расчет звездного времени по Гринвичу»,« Морской океанографический портал ».
- ^ Рой А.Э. 1978 Орбитальное движение, (Адам Хильгер ISBN 0-85274-228-2)
- ^ а б Моултон F R 1970 Введение в небесную механику, второе исправленное издание, (Нью-Йорк: Дувр).
- ^ Hinch E J 1991 Методы возмущений, (Кембридж: издательство Кембриджского университета)
- ^ Burington R S 1949 г. Справочник математических таблиц и формул (Сандаски, Огайо: Издательство Справочника)
- ^ Whitman A M 2007, "Простое выражение для уравнения времени", Журнал Североамериканского общества солнечных часов 14 С. 29–33.
- ^ а б Милн Р. М. 1921, «Заметка об уравнении времени», Математический вестник 10 (The Mathematical Association) стр. 372–375.
- ^ Muller M 1995, "Уравнение времени - проблема астрономии", Acta Phys Pol A 88 Дополнение, С-49.
- ^ а б Уильямс, Дэвид О. (2009). «Широта и долгота Солнца». Архивировано из оригинал 23 марта 2012 г.
- ^ "Приблизительные солнечные координаты»,« Морской океанографический портал ».
- ^ Военно-морская обсерватория США Апрель 2010, Многолетний интерактивный компьютерный альманах (версия 2.2.1), Ричмонд VA: Willmann-Bell.
Рекомендации
- Геляр, А. "Солнечные данные". Архивировано из оригинал 11 января 2004 г.
- Миус, Дж (1997). Математическая астрономия кусочки. Ричмонд, Вирджиния: Уиллман-Белл.CS1 maint: ref = harv (связь)
- Маккарти, Деннис Д.; Зайдельманн, П. Кеннет (2009). ВРЕМЯ от вращения Земли к атомной физике. Вайнхайм: Wiley VCH. ISBN 978-3-527-40780-4.CS1 maint: ref = harv (связь)
внешняя ссылка
| Викискладе есть медиафайлы по теме Уравнение времени (солнечные часы). |
- Солнечный калькулятор NOAA
- Услуги передачи данных USNO (включая время восхода / захода / прохождения Солнца и других небесных объектов)
- Уравнение времени описано на Королевская Гринвичская обсерватория интернет сайт
- Сайт аналеммы с множеством иллюстраций
- Уравнение времени и аналемма, Кирон Тейлор
- Статья Брайана Тунга содержащий ссылку на программу на языке C, использующую более точную формулу, чем большинство других (особенно при больших наклонах и эксцентриситетах). Программа может рассчитывать склонение Солнца, Уравнение времени или Аналемму.
- Выполнение расчетов с использованием геоцентрических моделей планет Птолемея с обсуждением его работы Э. график
- Уравнение времени с длинными часами Джона Топпинга C.1720
- Уравнение временной поправочной таблицы Страница с описанием того, как привести часы в соответствие с солнечными часами.
- Солнечный темпометр - Рассчитайте солнечное время, включая уравнение времени.