WikiDer > Большой триамбический икосаэдр - Википедия

	Большой триамбический икосаэдр	Медиальный триамбический икосаэдр
Типы	Двойные однородные многогранники
Группа симметрии	ячас
Имя	Большой триамбический икосаэдр	Медиальный триамбический икосаэдр
Указатель ссылок	DU47, W34, 30/59	DU41, W34, 30/59
Элементы	F = 20, E = 60 V = 32 (χ = -8)	F = 20, E = 60 V = 24 (χ = -16)
Изогранные грани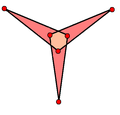
Duals	Большой дитригональный икосододекаэдр	Дитригональный додекадодекаэдр
Звездчатость
Икосаэдр: W34
Звездчатая диаграмма

3D модель среднего триамбического икосаэдра

3D модель большого триамбического икосаэдра

В геометрия, то большой триамбический икосаэдр и медиальный триамбический икосаэдр (или же среднетриамбический икосаэдр) визуально идентичны двойной равномерные многогранники. Внешняя поверхность также представляет собой Де₂ж₂ звездчатость из икосаэдр. Эти цифры можно отличить, отметив, какие пересечения между краями верны. вершины а какие нет. На изображениях выше истинные вершины отмечены золотыми сферами, которые можно увидеть в вогнутых Y-образных областях. В качестве альтернативы, если грани заполнены четно-нечетное правило, внутренняя структура обеих фигур будет отличаться.

12 вершин выпуклый корпус соответствует расположение вершин из икосаэдр.

Большой триамбический икосаэдр

В большой триамбический икосаэдр является двойником большой дитригональный икосододекаэдр, U47. Он имеет 20 перевернутых шестиугольников (триамбус) лица, по форме напоминающие трехлопастные пропеллер. У него 32 вершины: 12 внешних точек и 20 скрытых внутри. Имеет 60 граней.

Грани имеют чередующиеся углы ${ displaystyle arccos ({ frac {1} {4}}) - 60 ^ { circ} приблизительно 15.522 , 487 , 814 , 07 ^ { circ}}$ и ${ displaystyle arccos (- { frac {1} {4}}) приблизительно 104,477 , 512 , 185 , 93 ^ { circ}}$. Сумма шести углов равна ${ displaystyle 360 ​​^ { circ}}$, и нет ${ displaystyle 720 ^ { circ}}$ как и следовало ожидать от шестиугольника, потому что многоугольник дважды поворачивается вокруг своего центра. В двугранный угол равно ${ displaystyle arccos (- { frac {1} {3}}) приблизительно 109.471 , 220 , 634 , 49}$.

Медиальный триамбический икосаэдр

В медиальный триамбический икосаэдр является двойником дитригональный додекадодекаэдр, U41. У него 20 граней, каждая из которых простая вогнутая. изогональный шестиугольники или же триамби. У него 24 вершины: 12 внешних точек и 12 скрытых внутри. Имеет 60 граней.

Грани имеют чередующиеся углы ${ displaystyle arccos ({ frac {1} {4}}) - 60 ^ { circ} приблизительно 15.522 , 487 , 814 , 07 ^ { circ}}$ и ${ displaystyle arccos (- { frac {1} {4}}) + 120 ^ { circ} приблизительно 224,477 , 512 , 185 , 93 ^ { circ}}$. В двугранный угол равно ${ displaystyle arccos (- { frac {1} {3}}) приблизительно 109.471 , 220 , 634 , 49}$.

В отличие от большого триамбического икосаэдра, средний триамбический икосаэдр топологически является правильный многогранник индекса два.^[1] Искажая триамби в обычный шестиугольники, получаем факторпространство гиперболический гексагональная черепица порядка 5:

Как звездочка

это Веннингера 34-я модель как его 9-я звездочка икосаэдра

Смотрите также

• Триакис икосаэдр
• Малый триамбический икосаэдр
• Средний ромбический триаконтаэдр

Рекомендации

• Веннингер, Магнус (1974). Модели многогранников. Издательство Кембриджского университета. ISBN 0-521-09859-9.
• Веннингер, Магнус (1983). Двойные модели. Издательство Кембриджского университета. ISBN 978-0-521-54325-5. МИСТЕР 0730208.
• H.S.M. Coxeter, Правильные многогранники, (3-е издание, 1973 г.), Дуврское издание, ISBN 0-486-61480-8, 3.6 6.2 Звездчатые тела Платоновых тел, стр.96-104

внешняя ссылка

• Вайсштейн, Эрик В. «Большой триамбический икосаэдр». MathWorld.
• Вайсштейн, Эрик В. «Медиальный триамбический икосаэдр». MathWorld.
• gratrix.net Равномерные многогранники и двойники
• bulatov.org Медиальный триамбический икосаэдр Большой триамбический икосаэдр

Примечательный звёздчатые формы икосаэдра
Обычный	Униформа двойников			Обычные соединения			Обычная звезда	Другие
(Выпуклый) икосаэдр	Малый триамбический икосаэдр	Медиальный триамбический икосаэдр	Большой триамбический икосаэдр	Соединение пяти октаэдров	Соединение пяти тетраэдров	Соединение десяти тетраэдров	Большой икосаэдр	Раскопанный додекаэдр	Окончательная звездчатость
Процесс образования звезд на икосаэдре создает ряд связанных многогранники и соединения с икосаэдрическая симметрия.