WikiDer > Второй закон термодинамики
| Термодинамика | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
 Классический Тепловой двигатель Карно | ||||||||||||
| ||||||||||||
В второй закон термодинамики заявляет, что общая энтропия из изолированная система никогда не может уменьшаться с течением времени и является постоянным, если и только если все процессы обратимы.[1] Изолированные системы спонтанно развиваются в сторону термодинамическое равновесие, состояние с максимальной энтропией.
Полная энтропия системы и ее окружения может оставаться постоянной в идеальных случаях, когда система находится в термодинамическое равновесие, или проходит (фиктивный) обратимый процесс. Во всех происходящих процессах, в том числе спонтанные процессы,[2] общая энтропия системы и ее окружения увеличивается, и процесс необратимый в термодинамическом смысле. Увеличение энтропии объясняет необратимость природных процессов, а асимметрия между будущим и прошлым.[3]
Исторически второй закон был эмпирический вывод это было принято как аксиома термодинамическая теория. Статистическая механика, классический или квант, объясняет микроскопическое происхождение закона.
Второй закон выражался по-разному. Его первая формулировка приписывается французскому ученому. Сади Карно, который в 1824 году показал, что существует верхний предел эффективности преобразования тепла для работы в тепловой машине. Этот аспект второго закона часто назван в честь Карно.[4]
Вступление
В первый закон термодинамики дает определение внутренняя энергия из термодинамическая система, и выражает закон сохранение энергии.[5][6] Второй закон касается направления природных процессов.[7] Он утверждает, что естественный процесс протекает только в одном смысле и не является обратимым. Например, когда доступен путь для проводимости и излучения, тепло всегда спонтанно перетекает от более горячего тела к более холодному. Такой явления учитываются в энтропия.[8][9] Если изолированная система изначально поддерживается во внутреннем термодинамическом равновесии за счет внутреннего разделения непроницаемых стенок, а затем какая-то операция делает стенки более проницаемыми, тогда система спонтанно эволюционирует, чтобы достичь окончательного нового внутреннего термодинамического равновесия, и ее полная энтропия S, увеличивается.
В фиктивном обратимом процессе бесконечно малое приращение энтропии (dS) системы определяется как результат бесконечно малой передачи тепла (δQ) к закрытая система (что позволяет входить или выходить энергии, но не переносит материю), деленную на общую температуру (Т) системы в равновесии и окружающей среды, которая поставляет тепло:[10]
Для бесконечно малых количеств тепла используются разные обозначения (δ) и бесконечно малые количества энтропии (d), поскольку энтропия функция государства, а тепла, как и работы, нет. Для реально возможного бесконечно малого процесса без обмена массой с окружающей средой второй закон требует, чтобы приращение энтропии системы соответствовало неравенство [11][12]
Это связано с тем, что общий процесс для этого случая может включать в себя работу, выполняемую в системе ее окружением, что может иметь эффекты трения или вязкости внутри системы, потому что может происходить химическая реакция или потому что теплопередача на самом деле происходит только необратимо, обусловлено конечной разницей между температурой системы (Т) и температура окружающей среды (ТSurr).[13][14] Обратите внимание, что равенство все еще применяется для чистого теплового потока,[15]
что является основой точного определения абсолютной энтропии чистых веществ по измеренным кривым теплоемкости и изменений энтропии при фазовых переходах, т. е. калориметрическим методом.[16][11] Представляем набор внутренних переменных для описания отклонения термодинамической системы от физического равновесия (с требуемым четко определенным равномерным давлением п и температура Т)[15] из состояния химического равновесия можно записать равенство
Второй член представляет работу внутренних переменных, которые могут быть нарушены внешними воздействиями, но система не может выполнять какую-либо положительную работу через внутренние переменные. Это утверждение вводит невозможность обращения эволюции термодинамической системы во времени и может рассматриваться как формулировка второй принцип термодинамики - формулировка, которая, конечно, эквивалентна формулировке принципа в терминах энтропии.[17][18]
В нулевой закон термодинамики в его обычном кратком изложении позволяет распознать, что два тела в отношении теплового равновесия имеют одинаковую температуру, особенно то, что тестовое тело имеет ту же температуру, что и эталонное термометрическое тело.[19] Для одного тела, находящегося в тепловом равновесии с другим, существует неограниченное количество эмпирических температурных шкал, как правило, в зависимости от свойств конкретного эталонного термометрического тела. Второй закон позволяет[как?] выделенная шкала температур, определяющая абсолютную, термодинамическая температура, независимо от свойств какого-либо конкретного эталонного термометрического тела.[20][21]
Различные положения закона
Второй закон термодинамики можно выразить по-разному:[22] самые известные классические высказывания[23] являясь заявлением Рудольф Клаузиус (1854), заявление Лорд Кельвин (1851), и утверждение в аксиоматической термодинамике Константин Каратеодори (1909). Эти утверждения формулируют закон в общих физических терминах, ссылаясь на невозможность определенных процессов. Утверждения Клаузиуса и Кельвина эквивалентны.[24]
Принцип Карно
Историческое происхождение[25] второго начала термодинамики был в принципе Карно. Это относится к циклу Тепловой двигатель Карно, фиктивно работают в предельном режиме экстремальной медленности, известном как квазистатический, так что передача тепла и работы происходит между подсистемами, которые всегда находятся в своих собственных внутренних состояниях термодинамического равновесия. Двигатель Карно - это идеализированное устройство, представляющее особый интерес для инженеров, которым важна эффективность тепловых двигателей. Принцип Карно был признан Карно в то время, когда теория калорий жары серьезно рассматривались, прежде чем было признано первый закон термодинамики, и до математического выражения понятия энтропии. Интерпретируемый в свете первого закона, он физически эквивалентен второму закону термодинамики и остается в силе сегодня. Первоначальные аргументы Карно были сделаны с точки зрения теории теплоты еще до открытия первого закона термодинамики. Вот несколько примеров из его книги:
- ...везде, где существует разница температур, может возникать движущая сила.[26]
- Таким образом, производство движущей силы в паровых двигателях связано не с фактическим потреблением калорий, а с к его транспортировке от теплого тела к холодному ...[27]
- Движущая сила тепла не зависит от агентов, задействованных для его реализации; его количество определяется исключительно температурами тел, между которыми осуществляется, наконец, передача калорий.[28]
Говоря современным языком, принцип Карно можно сформулировать более точно:
- Эффективность квазистатического или обратимого цикла Карно зависит только от температур двух тепловых резервуаров и одинакова для любого рабочего тела. Двигатель Карно, работающий таким образом, является наиболее эффективным тепловым двигателем, использующим эти две температуры.[29][30][31][32][33][34]
Заявление Клаузиуса
Немецкий ученый Рудольф Клаузиус заложил основу второго закона термодинамики в 1850 году, исследуя связь между теплопередачей и работой.[35] Его формулировка второго закона, опубликованная на немецком языке в 1854 году, известна как Заявление Клаузиуса:
Тепло никогда не может перейти от более холодного тела к более теплому без каких-либо других связанных с этим изменений, происходящих в то же время.[36]
В заявлении Клаузиуса используется понятие «прохождения тепла». Как обычно в дискуссиях по термодинамике, это означает «чистую передачу энергии в виде тепла» и не относится к способствующей передаче в ту или иную сторону.
Тепло не может спонтанно перетекать из холодных регионов в горячие без выполнения внешней работы в системе, что очевидно из обычного опыта эксплуатации. охлаждение, Например. В холодильнике тепло перетекает из холодного в горячее, но только под воздействием внешнего агента, холодильной системы.
Утверждения Кельвина
Лорд Кельвин выразил второй закон в нескольких редакциях.
- Для самодействующей машины без посторонней помощи невозможно передать тепло от одного тела к другому при более высокой температуре.
- Невозможно с помощью неодушевленных материалов вызвать механический эффект из любой части материи, охладив ее ниже температуры самого холодного из окружающих объектов.[37]
Эквивалентность утверждений Клаузиуса и Кельвина
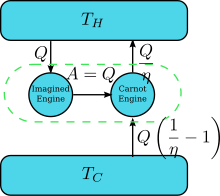
Предположим, что есть двигатель, нарушающий утверждение Кельвина: то есть двигатель, который отводит тепло и полностью циклически преобразует его в работу без каких-либо других результатов. Теперь соедините его с перевернутым Двигатель Карно как показано на рисунке. В эффективность нормального теплового двигателя η, поэтому эффективность обратного теплового двигателя составляет 1 / η. Чистый и единственный эффект объединенной пары двигателей заключается в передаче тепла. от более холодного резервуара к более горячему, что нарушает утверждение Клаузиуса. (Это следствие первый закон термодинамики, так как полная энергия системы не меняется, , И потому ). Таким образом, нарушение утверждения Кельвина подразумевает нарушение утверждения Клаузиуса, то есть утверждение Клаузиуса подразумевает утверждение Кельвина. Подобным образом мы можем доказать, что утверждение Кельвина влечет утверждение Клаузиуса, и, следовательно, они эквивалентны.
Предложение Планка
Планк выдвинул следующее предложение, выведенное непосредственно из опыта. Иногда это считают его утверждением второго закона, но он считал это отправной точкой для вывода второго закона.
Связь между утверждением Кельвина и предложением Планка
В учебниках почти принято говорить о "Заявление Кельвина-Планка"закона, как, например, в тексте тер Хаар и Вергеланд.[40]
В Заявление Кельвина-Планка (или заявление о тепловом двигателе) второго начала термодинамики утверждает, что
- Невозможно придумать циклически управляющее устройство, единственным действием которого является поглощение энергии в виде тепла от одного термальный резервуар и доставить эквивалентную сумму работай.[41]
Заявление Планка
Планк сформулировал второй закон следующим образом.
Утверждение Планка очень похоже на утверждение Уленбека и Форда для необратимые явления.
- ... при необратимом или самопроизвольном переходе от одного состояния равновесия к другому (как, например, выравнивание температур двух тел A и B при контакте) энтропия всегда увеличивается.[45]
Принцип Каратеодори
Константин Каратеодори сформулировал термодинамику на чисто математической аксиоматической основе. Его утверждение второго закона известно как принцип Каратеодори, который можно сформулировать следующим образом:[46]
В каждой окрестности любого состояния S адиабатически замкнутой системы есть состояния, недоступные из S.[47]
В этой формулировке он описал концепцию адиабатическая доступность впервые и заложил основу для нового раздела классической термодинамики, часто называемого геометрическая термодинамика. Из принципа Каратеодори следует, что количество энергии, квазистатически передаваемое в виде тепла, является голономным. функция процесса, другими словами, .[48][требуется разъяснение]
Хотя в учебниках почти принято говорить, что принцип Каратеодори выражает второй закон, и рассматривать его как эквивалент утверждений Клаузиуса или Кельвина-Планка, это не так. Чтобы получить полное содержание второго закона, принцип Каратеодори должен быть дополнен принципом Планка, согласно которому изохорная работа всегда увеличивает внутреннюю энергию замкнутой системы, которая изначально находилась в своем собственном внутреннем термодинамическом равновесии.[14][49][50][51][требуется разъяснение]
Принцип Планка
В 1926 г. Макс Планк написал важную статью по основам термодинамики.[50][52] Он указал на принцип
Эта формулировка не упоминает тепло и не упоминает температуру или даже энтропию и не обязательно косвенно полагается на эти концепции, но подразумевает содержание второго закона. Тесно связанное с этим утверждение состоит в том, что «давление трения никогда не дает положительного результата».[53] Планк писал: «Выделение тепла трением необратимо».[54][55]
Не говоря уже об энтропии, этот принцип Планка сформулирован в физических терминах. Это очень близко связано с утверждением Кельвина, приведенным выше.[56] Актуально, что для системы с постоянным объемом и число родинок, энтропия является монотонной функцией внутренней энергии. Тем не менее, этот принцип Планка на самом деле не является предпочтительным утверждением Планка второго закона, который цитируется выше в предыдущем подразделе настоящего раздела данной статьи, и основан на концепции энтропии.
Утверждение, в некотором смысле дополняющее принцип Планка, сделано Боргнакке и Зоннтагом. Они не предлагают это как полную формулировку второго закона:
- ... есть только один способ уменьшить энтропию [замкнутой] системы - это передача тепла от системы.[57]
В отличие от только что изложенного выше принципа Планка, этот принцип явно связан с изменением энтропии. Удаление вещества из системы также может уменьшить ее энтропию.
Утверждение для системы, у которой есть известное выражение ее внутренней энергии как функции ее обширных переменных состояния
Было показано, что второй закон эквивалентен внутренняя энергия U будучи слабым выпуклая функция, когда записано как функция от обширных свойств (масса, объем, энтропия, ...).[58][59][требуется разъяснение]
Следствия
Вечный двигатель второго рода
До установления второго закона многие люди, заинтересованные в изобретении вечного двигателя, пытались обойти ограничения первый закон термодинамики за счет извлечения огромной внутренней энергии окружающей среды как мощности машины. Такая машина называется «вечным двигателем второго рода». Второй закон декларировал невозможность создания таких машин.
Теорема Карно
Теорема Карно (1824) - это принцип, ограничивающий максимальную эффективность любого возможного двигателя. Эффективность зависит исключительно от разницы температур между горячим и холодным тепловыми резервуарами. Теорема Карно гласит:
- Все необратимые тепловые двигатели между двумя тепловыми резервуарами менее эффективны, чем Двигатель Карно между одними и теми же резервуарами.
- Все реверсивные тепловые двигатели между двумя тепловыми резервуарами одинаково эффективны с двигателем Карно, работающим между одними и теми же резервуарами.
В его идеальной модели теплота калорий, преобразованная в работу, могла быть восстановлена путем обращения движения цикла, концепция, впоследствии известная как термодинамическая обратимость. Карно, однако, предположил, что некоторая часть калорий теряется, а не превращается в механическую работу. Следовательно, ни одна настоящая тепловая машина не могла реализовать Цикл Карнообратимость и была признана менее эффективной.
Хотя сформулировано с точки зрения калорийности (см. Устаревшее теория калорий), скорее, чем энтропия, это было ранним пониманием второго закона.
Неравенство Клаузиуса
В Теорема Клаузиуса (1854) утверждает, что в циклическом процессе
В обратимом случае имеет место равенство[60] и в необратимом случае выполняется строгое неравенство. Обратимый случай используется для введения функции состояния энтропия. Это связано с тем, что в циклических процессах изменение функции состояния равно нулю от функции состояния.
Термодинамическая температура
Для произвольной тепловой машины КПД составляет:
куда Wп для чистой работы, выполненной за цикл. Таким образом, эффективность зависит только от qC/ qЧАС.
Теорема Карно утверждает, что все реверсивные двигатели, работающие между одними и теми же тепловыми резервуарами, одинаково эффективны. Таким образом, любой реверсивный тепловой двигатель, работающий между температурами Т1 и Т2 должны иметь одинаковую эффективность, то есть эффективность зависит только от температуры:
Кроме того, реверсивный тепловой двигатель, работающий между температурами Т1 и Т3 должен иметь такую же эффективность, как и цикл, состоящий из двух циклов, один между Т1 и другая (промежуточная) температура Т2, а второй между Т2 иТ3. Это может быть только в том случае, если
Теперь рассмотрим случай, когда фиксированная эталонная температура: температура тройная точка воды. Тогда для любого Т2 и Т3,
Следовательно, если термодинамическая температура определяется как
тогда функция ж, рассматриваемая как функция термодинамической температуры, просто
и эталонная температура Т1 будет иметь значение 273,16. (Можно использовать любую эталонную температуру и любое положительное числовое значение - выбор здесь соответствует Кельвин шкала.)
Энтропия
Согласно Равенство Клаузиуса, для обратимого процесса
Это означает, что линейный интеграл не зависит от пути для обратимых процессов.
Таким образом, мы можем определить функцию состояния S, называемую энтропией, которая для обратимого процесса или для чистой теплопередачи[15] удовлетворяет
При этом мы можем получить разность энтропии, только интегрировав приведенную выше формулу. Для получения абсолютного значения нам понадобится третий закон термодинамики, в котором говорится, что S = 0 при абсолютный ноль для идеальных кристаллов.
Для любого необратимого процесса, поскольку энтропия является функцией состояния, мы всегда можем связать начальное и конечное состояния с воображаемым обратимым процессом и интегрировать на этом пути для вычисления разницы в энтропии.
Теперь измените обратимый процесс и объедините его с указанным необратимым процессом. Применяя Неравенство Клаузиуса в этом цикле,
Таким образом,
где равенство имеет место, если преобразование обратимо.
Обратите внимание, что если процесс адиабатический процесс, тогда , так .
Энергия, доступная полезная работа
Важным и показательным идеализированным частным случаем является рассмотрение применения Второго закона к сценарию изолированной системы (называемой целостной системой или вселенной), состоящей из двух частей: интересующей подсистемы и окружения подсистемы. Эти окрестности кажутся настолько большими, что их можно рассматривать как неограниченный резервуар тепла при температуре Тр и давление пр - чтобы независимо от того, сколько тепла передается в подсистему (или от нее), температура окружающей среды остается Тр; и независимо от того, насколько объем подсистемы расширяется (или сжимается), давление окружающей среды останется пр.
Что бы ни изменилось dS и dSр происходят в энтропиях подсистемы и окружения индивидуально, согласно Второму закону энтропия Sмалыш изолированной общей системы не должно уменьшаться:
Согласно первый закон термодинамики, перемена dU во внутренней энергии подсистемы - это сумма тепла δq добавлен в подсистему, меньше любая работа δw сделано к подсистема, плюс любая чистая химическая энергия, поступающая в подсистему d ∑μiRNя, так что:
где μiR являются химические потенциалы химических веществ во внешней среде.
Теперь тепло выходит из резервуара и поступает в подсистему.
где мы впервые использовали определение энтропии в классической термодинамике (альтернативно, в статистической термодинамике можно вывести связь между изменением энтропии, температурой и поглощенным теплом); а затем неравенство Второго закона сверху.
Следовательно, любая сетевая работа δw выполняемые подсистемой должны подчиняться
Полезно разделить работу δw выполняется подсистемой в полезный работай δwты это можно сделать к подсистема, сверх работы пр dV выполняется просто за счет расширения подсистемы против окружающего внешнего давления, что дает следующее соотношение для полезной работы (эксергии), которая может быть выполнена:
Правую часть удобно определить как точную производную термодинамического потенциала, называемую доступность или же эксергия E подсистемы,
Таким образом, Второй закон подразумевает, что для любого процесса, который можно рассматривать как просто разделенный на подсистему и неограниченный резервуар температуры и давления, с которым он контактирует,
т.е. изменение эксергии подсистемы плюс проделанная полезная работа к подсистема (или, изменение эксергии подсистемы за вычетом какой-либо работы, в дополнение к той, которая выполняется резервуаром давления, выполненной на система) должно быть меньше или равно нулю.
В общем, если правильно бесконечный резервуар эталонное состояние выбирается в качестве системного окружения в реальном мире, тогда Второй закон предсказывает уменьшение E для необратимого процесса и без изменений для обратимого процесса.
- Эквивалентно
Это выражение вместе с соответствующим ссылочным состоянием позволяет инженер-проектировщик работает в макроскопическом масштабе (над термодинамический предел), чтобы использовать Второй закон без прямого измерения или учета изменения энтропии в полностью изолированной системе. (Также см Инженер-технолог). Эти изменения уже были учтены в предположении, что рассматриваемая система может достичь равновесия с эталонным состоянием без изменения эталонного состояния. Также может быть найдена эффективность процесса или совокупности процессов, которая сравнивает его с обратимым идеалом (Видеть эффективность второго закона.)
Такой подход ко Второму закону широко используется в инженерное дело упражняться, экологический учет, системная экология, и другие дисциплины.
Второй закон химической термодинамики
Для самопроизвольный химический процесс в замкнутой системе при постоянной температуре и давлении безPV работы неравенство Клаузиуса ΔS> Q / TSurr превращается в условие изменения Свободная энергия Гиббса
или dграмм <0. Для аналогичного процесса при постоянной температуре и объеме изменение Свободная энергия Гельмгольца должно быть отрицательным, . Таким образом, отрицательное значение изменения свободной энергии (G или A) является необходимым условием для того, чтобы процесс был спонтанным. Это наиболее полезная форма второго закона термодинамики в химии, где изменения свободной энергии могут быть рассчитаны из табличных энтальпий образования и стандартных молярных энтропий реагентов и продуктов.[16] [11] Условие химического равновесия при постоянном Т и п без электромонтажных работ dграмм = 0.
История

Первая теория преобразования тепла в механическую работу возникла благодаря Николя Леонар Сади Карно в 1824 году. Он был первым, кто правильно понял, что эффективность этого преобразования зависит от разницы температур между двигателем и окружающей средой.
Признавая важность Джеймс Прескотт Джоульработа по сохранению энергии, Рудольф Клаузиус был первым, кто сформулировал второй закон в 1850 году в такой форме: тепло не течет спонтанно от холодных тел к горячим. Хотя сейчас общеизвестно, это противоречило теория калорий тепла, популярного в то время, когда тепло считалось жидкостью. Отсюда он смог вывести принцип Сади Карно и определение энтропии (1865 г.).
Основанный в 19 веке, Утверждение Кельвина-Планка о втором законе говорит: "Это невозможно для любого устройства, которое работает на цикл получать тепло от одного резервуар и произвести чистый объем работы ». Было показано, что это эквивалентно утверждению Клаузиуса.
В эргодическая гипотеза также важно для Больцман подход. В нем говорится, что в течение длительных периодов времени время, проведенное в некоторой области фазового пространства микросостояний с одинаковой энергией, пропорционально объему этой области, то есть все доступные микросостояния равновероятны в течение длительного периода времени. В равной степени здесь говорится, что среднее по времени и среднее по статистическому ансамблю одинаковы.
Существует традиционная доктрина, начиная с Клаузиуса, что энтропию можно понять в терминах молекулярного «беспорядка» внутри макроскопическая система. Эта доктрина устарела.[61][62][63]
Счет предоставлен Клаузиусом
В 1856 г. немецкий физик Рудольф Клаузиус сформулировал то, что он назвал «второй фундаментальной теоремой в механическая теория тепла"в следующей форме:[64]
куда Q тепло, Т это температура и N представляет собой «эквивалентную стоимость» всех нескомпенсированных преобразований, включенных в циклический процесс. Позже, в 1865 году, Клаузиус определил «эквивалентность-ценность» как энтропию. Вслед за этим определением в том же году наиболее известная версия второго закона была прочитана на презентации в Цюрихском философском обществе 24 апреля, в которой в конце своего выступления Клаузиус заключает:
Энтропия Вселенной стремится к максимуму.
Это утверждение - самая известная формулировка второго закона. Из-за расплывчатости его языка, например вселенная, а также отсутствие особых условий, например открытый, закрытый или изолированный, многие люди принимают это простое утверждение за то, что второй закон термодинамики применим практически ко всем вообразимым предметам. Это неправда; это утверждение - только упрощенная версия более расширенного и точного описания.
С точки зрения изменения времени математическая формулировка второго закона для изолированная система подвергается произвольному преобразованию:
куда
- S - энтропия системы и
- т является время.
Знак равенства применяется после уравновешивания. Альтернативный способ формулировки второго закона для изолированных систем:
- с
с сумма ставки производство энтропии всеми процессами внутри системы. Преимущество этой формулировки состоит в том, что она показывает эффект производства энтропии. Скорость производства энтропии - очень важное понятие, поскольку оно определяет (ограничивает) эффективность тепловых машин. Умножается на температуру окружающей среды дает так называемую рассеянную энергию .
Выражение второго закона для закрытых систем (т.е. допускающих теплообмен и движущиеся границы, но не обмен веществ):
- с
Здесь
- тепловой поток в систему
- - температура в точке, где тепло входит в систему.
Знак равенства имеет место в том случае, если внутри системы происходят только обратимые процессы. Если имеют место необратимые процессы (что имеет место в реальных действующих системах), сохраняется знак>. Если тепло поступает в систему в нескольких местах, мы должны вычислить алгебраическую сумму соответствующих членов.
Для открытых систем (также допускающих обмен веществ):
- с
Здесь представляет собой поток энтропии в систему, связанный с потоком вещества, поступающего в систему. Его не следует путать с производной энтропии по времени. Если материя поступает в несколько мест, мы должны взять алгебраическую сумму этих вкладов.
Статистическая механика
Статистическая механика дает объяснение второму закону, постулируя, что материал состоит из атомов и молекул, которые находятся в постоянном движении. Конкретный набор положений и скоростей для каждой частицы в системе называется микросостояние системы и из-за постоянного движения система постоянно меняет свое микросостояние. Статистическая механика постулирует, что в равновесии каждое микросостояние, в котором может находиться система, имеет одинаковую вероятность, и когда это предположение делается, оно напрямую приводит к выводу, что второй закон должен выполняться в статистическом смысле. То есть второй закон будет выполняться в среднем со статистической вариацией порядка 1 /√N куда N - количество частиц в системе. Для повседневных (макроскопических) ситуаций вероятность нарушения второго закона практически равна нулю. Однако для систем с небольшим числом частиц термодинамические параметры, включая энтропию, могут показывать значительные статистические отклонения от предсказываемых вторым законом. Классическая термодинамическая теория не занимается этими статистическими вариациями.
Вывод из статистической механики
Первый механический аргумент Кинетическая теория газов что молекулярные столкновения влекут за собой выравнивание температур и, следовательно, стремление к равновесию объясняется тем, что Джеймс Клерк Максвелл в 1860 г .;[65] Людвиг Больцманн с его H-теорема 1872 г. также утверждал, что из-за столкновений газы должны со временем стремиться к Распределение Максвелла – Больцмана.
Из-за Парадокс лошмидта, выводы Второго закона должны делать предположение относительно прошлого, а именно, что система некоррелированный когда-то в прошлом; это позволяет проводить простую вероятностную обработку. Это предположение обычно рассматривается как граничное условие, и, таким образом, второй Закон в конечном итоге является следствием начальных условий где-то в прошлом, вероятно, в начале Вселенной ( Большой взрыв), хотя другие сценарии также были предложены.[66][67][68]
Учитывая эти допущения, в статистической механике Второй закон не является постулатом, а является следствием фундаментальный постулат, также известный как постулат равной априорной вероятности, если ясно, что простые аргументы вероятности применяются только к будущему, тогда как для прошлого существуют вспомогательные источники информации, которые говорят нам, что это была низкая энтропия.[нужна цитата] The first part of the second law, which states that the entropy of a thermally isolated system can only increase, is a trivial consequence of the equal prior probability postulate, if we restrict the notion of the entropy to systems in thermal equilibrium. The entropy of an isolated system in thermal equilibrium containing an amount of energy of является:
куда is the number of quantum states in a small interval between и . Здесь is a macroscopically small energy interval that is kept fixed. Strictly speaking this means that the entropy depends on the choice of . However, in the thermodynamic limit (i.e. in the limit of infinitely large system size), the specific entropy (entropy per unit volume or per unit mass) does not depend on .
Suppose we have an isolated system whose macroscopic state is specified by a number of variables. These macroscopic variables can, e.g., refer to the total volume, the positions of pistons in the system, etc. Then will depend on the values of these variables. If a variable is not fixed, (e.g. we do not clamp a piston in a certain position), then because all the accessible states are equally likely in equilibrium, the free variable in equilibrium will be such that is maximized as that is the most probable situation in equilibrium.
If the variable was initially fixed to some value then upon release and when the new equilibrium has been reached, the fact the variable will adjust itself so that is maximized, implies that the entropy will have increased or it will have stayed the same (if the value at which the variable was fixed happened to be the equilibrium value).Suppose we start from an equilibrium situation and we suddenly remove a constraint on a variable. Then right after we do this, there are a number of accessible microstates, but equilibrium has not yet been reached, so the actual probabilities of the system being in some accessible state are not yet equal to the prior probability of . We have already seen that in the final equilibrium state, the entropy will have increased or have stayed the same relative to the previous equilibrium state. Boltzmann's H-theorem, however, proves that the quantity ЧАС increases monotonically as a function of time during the intermediate out of equilibrium state.
Derivation of the entropy change for reversible processes
The second part of the Second Law states that the entropy change of a system undergoing a reversible process is given by:
where the temperature is defined as:
Видеть здесь for the justification for this definition. Suppose that the system has some external parameter, x, that can be changed. In general, the energy eigenstates of the system will depend on x. Согласно адиабатическая теорема of quantum mechanics, in the limit of an infinitely slow change of the system's Hamiltonian, the system will stay in the same energy eigenstate and thus change its energy according to the change in energy of the energy eigenstate it is in.
The generalized force, X, corresponding to the external variable x is defined such that is the work performed by the system if x is increased by an amount dx. E.g., if x is the volume, then X is the pressure. The generalized force for a system known to be in energy eigenstate дан кем-то:
Since the system can be in any energy eigenstate within an interval of , we define the generalized force for the system as the expectation value of the above expression:
To evaluate the average, we partition the energy eigenstates by counting how many of them have a value for within a range between и . Calling this number , у нас есть:
The average defining the generalized force can now be written:
We can relate this to the derivative of the entropy with respect to x at constant energy E as follows. Suppose we change x to x + dx. потом will change because the energy eigenstates depend on x, causing energy eigenstates to move into or out of the range between и . Let's focus again on the energy eigenstates for which lies within the range between и . Since these energy eigenstates increase in energy by Y dx, all such energy eigenstates that are in the interval ranging from E – Y dx to E move from below E to above E. There are
such energy eigenstates. Если , all these energy eigenstates will move into the range between и and contribute to an increase in . The number of energy eigenstates that move from below to above дан кем-то . Разница
is thus the net contribution to the increase in . Note that if Y dx is larger than there will be the energy eigenstates that move from below E to above . They are counted in both и , therefore the above expression is also valid in that case.
Expressing the above expression as a derivative with respect to E and summing over Y yields the expression:
The logarithmic derivative of with respect to x is thus given by:
The first term is intensive, i.e. it does not scale with system size. In contrast, the last term scales as the inverse system size and will thus vanish in the thermodynamic limit. We have thus found that:
Combining this with
Gives:
Derivation for systems described by the canonical ensemble
If a system is in thermal contact with a heat bath at some temperature T then, in equilibrium, the probability distribution over the energy eigenvalues are given by the канонический ансамбль:
Here Z is a factor that normalizes the sum of all the probabilities to 1, this function is known as the функция распределения. We now consider an infinitesimal reversible change in the temperature and in the external parameters on which the energy levels depend. It follows from the general formula for the entropy:
который
Inserting the formula for for the canonical ensemble in here gives:
Initial conditions at the Big Bang
As elaborated above, it is thought that the second law of thermodynamics is a result of the very low-entropy initial conditions at the Большой взрыв. From a statistical point of view, these were very special conditions. On the other hand, they were quite simple, as the universe - or at least the part thereof from which the наблюдаемая вселенная developed - seem to have been extremely uniform.[69]
This may seem somewhat paradoxical, since in many physical systems uniform conditions (e.g. mixed rather than separated gases) have high entropy. The paradox is solved once realizing that gravitational systems have negative heat capacity, so that when gravity is important, uniform conditions (e.g. gas of uniform density) in fact have lower entropy compared to non-uniform ones (e.g. black holes in empty space).[70] Yet another approach is that the universe had high (or even maximal) entropy given its size, but as the universe grew it rapidly came out of thermodynamic equilibrium, its entropy only slightly increased compared to the increase in maximal possible entropy, and thus it has arrived at a very low entropy when compared to the much larger possible maximum given its later size.[71]
As for the reason why initial conditions were such, one suggestion is that космологическая инфляция was enough to wipe off non-smoothness, while another is that the universe was created spontaneously where the mechanism of creation implies low-entropy initial conditions.[72]
Живые организмы
There are two principal ways of formulating thermodynamics, (a) through passages from one state of thermodynamic equilibrium to another, and (b) through cyclic processes, by which the system is left unchanged, while the total entropy of the surroundings is increased. These two ways help to understand the processes of life. The thermodynamics of living organisms has been considered by many authors, such as Эрвин Шредингер, Леон Бриллюэн[73] и Айзек Азимов.
To a fair approximation, living organisms may be considered as examples of (b). Approximately, an animal's physical state cycles by the day, leaving the animal nearly unchanged. Animals take in food, water, and oxygen, and, as a result of метаболизм, give out breakdown products and heat. Растения take in radiative energy from the sun, which may be regarded as heat, and carbon dioxide and water. They give out oxygen. In this way they grow. Eventually they die, and their remains rot away, turning mostly back into carbon dioxide and water. This can be regarded as a cyclic process. Overall, the sunlight is from a high temperature source, the sun, and its energy is passed to a lower temperature sink, i.e. radiated into space. This is an increase of entropy of the surroundings of the plant. Thus animals and plants obey the second law of thermodynamics, considered in terms of cyclic processes.
Furthermore, the ability of living organisms to grow and increase in complexity, as well as to form correlations with their environment in the form of adaption and memory, is not opposed to the second law - rather, it is akin to general results following from it: Under some definitions, an increase in entropy also results in an increase in complexity,[74] and for a finite system interacting with finite reservoirs, an increase in entropy is equivalent to an increase in correlations between the system and the reservoirs.[75]
Living organisms may be considered as open systems, because matter passes into and out from them. Thermodynamics of open systems is currently often considered in terms of passages from one state of thermodynamic equilibrium to another, or in terms of flows in the approximation of local thermodynamic equilibrium. The problem for living organisms may be further simplified by the approximation of assuming a steady state with unchanging flows. General principles of entropy production for such approximations are subject to unsettled current debate or research.
Gravitational systems
Commonly, systems for which gravity is not important have a positive теплоемкость, meaning that their temperature rises with their internal energy. Therefore, when energy flows from a high-temperature object to a low-temperature object, the source temperature decreases while the sink temperature is increased; hence temperature differences tend to diminish over time.
This is not always the case for systems in which the gravitational force is important: systems that are bound by their own gravity, such as stars, can have negative heat capacities. As they contract, both their total energy and their entropy decrease[76] but their their internal temperature may increase. This can be significant for протозвезды and even gas giant planets such as Юпитер.
As gravity is the most important force operating on cosmological scales, it may be difficult or impossible to apply the second law to the universe as a whole.[77]
Non-equilibrium states
The theory of classical or равновесная термодинамика is idealized. A main postulate or assumption, often not even explicitly stated, is the existence of systems in their own internal states of thermodynamic equilibrium. In general, a region of space containing a physical system at a given time, that may be found in nature, is not in thermodynamic equilibrium, read in the most stringent terms. In looser terms, nothing in the entire universe is or has ever been truly in exact thermodynamic equilibrium.[77][78]
For purposes of physical analysis, it is often enough convenient to make an assumption of термодинамическое равновесие. Such an assumption may rely on trial and error for its justification. If the assumption is justified, it can often be very valuable and useful because it makes available the theory of thermodynamics. Elements of the equilibrium assumption are that a system is observed to be unchanging over an indefinitely long time, and that there are so many particles in a system, that its particulate nature can be entirely ignored. Under such an equilibrium assumption, in general, there are no macroscopically detectable колебания. There is an exception, the case of critical states, which exhibit to the naked eye the phenomenon of критическая опалесценция. For laboratory studies of critical states, exceptionally long observation times are needed.
In all cases, the assumption of термодинамическое равновесие, once made, implies as a consequence that no putative candidate "fluctuation" alters the entropy of the system.
It can easily happen that a physical system exhibits internal macroscopic changes that are fast enough to invalidate the assumption of the constancy of the entropy. Or that a physical system has so few particles that the particulate nature is manifest in observable fluctuations. Then the assumption of thermodynamic equilibrium is to be abandoned. There is no unqualified general definition of entropy for non-equilibrium states.[79]
There are intermediate cases, in which the assumption of local термодинамическое равновесие is a very good approximation,[80][81][82][83] but strictly speaking it is still an approximation, not theoretically ideal.
For non-equilibrium situations in general, it may be useful to consider statistical mechanical definitions of other quantities that may be conveniently called 'entropy', but they should not be confused or conflated with thermodynamic entropy properly defined for the second law. These other quantities indeed belong to statistical mechanics, not to thermodynamics, the primary realm of the second law.
The physics of macroscopically observable fluctuations is beyond the scope of this article.
Стрела времени
The second law of thermodynamics is a physical law that is not symmetric to reversal of the time direction. This does not conflict with symmetries observed in the fundamental laws of physics (particularly Симметрия CPT) since the second law applies statistically on time-asymmetric boundary conditions.[84] The second law has been related to the difference between moving forwards and backwards in time, or to the principle that cause precedes effect (the causal arrow of time, или же причинность).[85]
Необратимость
Irreversibility in thermodynamic processes is a consequence of the asymmetric character of thermodynamic operations, and not of any internally irreversible microscopic properties of the bodies. Thermodynamic operations are macroscopic external interventions imposed on the participating bodies, not derived from their internal properties. There are reputed "paradoxes" that arise from failure to recognize this.
Парадокс лошмидта
Парадокс лошмидта, also known as the reversibility paradox, is the objection that it should not be possible to deduce an irreversible process from the time-symmetric dynamics that describe the microscopic evolution of a macroscopic system.
По мнению Шредингер, "It is now quite obvious in what manner you have to reformulate the law of entropy – or for that matter, all other irreversible statements – so that they be capable of being derived from reversible models. You must not speak of one isolated system but at least of two, which you may for the moment consider isolated from the rest of the world, but not always from each other."[86] The two systems are isolated from each other by the wall, until it is removed by the thermodynamic operation, as envisaged by the law. The thermodynamic operation is externally imposed, not subject to the reversible microscopic dynamical laws that govern the constituents of the systems. It is the cause of the irreversibility. The statement of the law in this present article complies with Schrödinger's advice. The cause–effect relation is logically prior to the second law, not derived from it.
Теорема Пуанкаре о возвращении
В Теорема Пуанкаре о возвращении considers a theoretical microscopic description of an isolated physical system. This may be considered as a model of a thermodynamic system after a thermodynamic operation has removed an internal wall. The system will, after a sufficiently long time, return to a microscopically defined state very close to the initial one. The Poincaré recurrence time is the length of time elapsed until the return. It is exceedingly long, likely longer than the life of the universe, and depends sensitively on the geometry of the wall that was removed by the thermodynamic operation. The recurrence theorem may be perceived as apparently contradicting the second law of thermodynamics. More obviously, however, it is simply a microscopic model of thermodynamic equilibrium in an isolated system formed by removal of a wall between two systems. For a typical thermodynamical system, the recurrence time is so large (many many times longer than the lifetime of the universe) that, for all practical purposes, one cannot observe the recurrence. One might wish, nevertheless, to imagine that one could wait for the Poincaré recurrence, and then re-insert the wall that was removed by the thermodynamic operation. It is then evident that the appearance of irreversibility is due to the utter unpredictability of the Poincaré recurrence given only that the initial state was one of thermodynamic equilibrium, as is the case in macroscopic thermodynamics. Even if one could wait for it, one has no practical possibility of picking the right instant at which to re-insert the wall. The Poincaré recurrence theorem provides a solution to Loschmidt's paradox. If an isolated thermodynamic system could be monitored over increasingly many multiples of the average Poincaré recurrence time, the thermodynamic behavior of the system would become invariant under time reversal.
Демон Максвелла
Эта секция не цитировать любой источники. (Август 2018 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Джеймс Клерк Максвелл imagined one container divided into two parts, А и B. Обе части заполнены одинаковым газ at equal temperatures and placed next to each other, separated by a wall. Наблюдая за молекулы с обеих сторон воображаемый демон guards a microscopic trapdoor in the wall. Когда молекула со скоростью быстрее средней из А летит к люку, демон открывает его, и молекула вылетает из А к B. Среднее скорость молекул в B будет увеличиваться в то время как в А в среднем они замедлятся. Поскольку средняя скорость молекул соответствует температуре, температура уменьшается в А и увеличивается в B, вопреки второму закону термодинамики.
One response to this question was suggested in 1929 by Leó Szilárd а позже Леон Бриллюэн. Сцилард указал, что реальный демон Максвелла должен иметь какие-то средства измерения молекулярной скорости и что получение информации потребует затрат энергии.
Maxwell's 'demon' repeatedly alters the permeability of the wall between А и B. It is therefore performing thermodynamic operations on a microscopic scale, not just observing ordinary spontaneous or natural macroscopic thermodynamic processes.
Котировки
| В Викицитатнике есть цитаты, связанные с: Второй закон термодинамики |
The law that entropy always increases holds, I think, the supreme position among the laws of Nature. If someone points out to you that your pet theory of the вселенная is in disagreement with Уравнения Максвелла – then so much the worse for Maxwell's equations. If it is found to be contradicted by observation – well, these experimentalists do bungle things sometimes. But if your theory is found to be against the second law of thermodynamics I can give you no hope; there is nothing for it but to collapse in deepest humiliation.
— сэр Артур Стэнли Эддингтон, The Nature of the Physical World (1927)
There have been nearly as many formulations of the second law as there have been discussions of it.
— Philosopher / Physicist П.В. Бриджмен, (1941)
Clausius is the author of the sibyllic utterance, "The energy of the universe is constant; the entropy of the universe tends to a maximum." The objectives of continuum thermomechanics stop far short of explaining the "universe", but within that theory we may easily derive an explicit statement in some ways reminiscent of Clausius, but referring only to a modest object: an isolated body of finite size.
— Truesdell, C., Muncaster, R. G. (1980). Fundamentals of Maxwell's Kinetic Theory of a Simple Monatomic Gas, Treated as a Branch of Rational Mechanics, Academic Press, New York, ISBN 0-12-701350-4, п. 17.
Смотрите также
Рекомендации
- ^ "5.2 Axiomatic Statements of the Laws of Thermodynamics". www.web.mit.edu. Массачусетский Институт Технологий.
- ^ Atkins and de Paula, p.78
- ^ Zohuri, Bahman (2016). Dimensional Analysis Beyond the Pi Theorem. Springer. п.111. ISBN 978-3-319-45726-0.
- ^ Jaffe, R.L., Taylor, W. (2018). The Physics of Energy, Cambridge University Press, Cambridge UK, pages 150, 151, 259, 772, 743.
- ^ Планк, М. (1897/1903), pp. 40–41.
- ^ Munster A. (1970), pp. 8–9, 50–51.
- ^ Mandl 1988
- ^ Планк, М. (1897/1903), pp. 79–107.
- ^ Bailyn, M. (1994), Section 71, pp. 113–154.
- ^ Байлин М. (1994), стр. 120.
- ^ а б c Mortimer, R. G. Физическая химия. 3rd ed., p. 120, Academic Press, 2008.
- ^ Fermi, E. Термодинамика, footnote on p. 48, Dover Publications,1956 (still in print).
- ^ Adkins, C.J. (1968/1983), p. 75.
- ^ а б c Münster, A. (1970), p. 45.
- ^ а б c Schmidt-Rohr, K. (2014). "Expansion Work without the External Pressure, and Thermodynamics in Terms of Quasistatic Irreversible Processes" J. Chem. Educ. 91: 402-409. https://dx.doi.org/10.1021/ed3008704
- ^ а б Oxtoby, D. W; Gillis, H.P., Butler, L. J. (2015).Принципы современной химии, Brooks Cole. п. 617. ISBN 978-1305079113
- ^ Pokrovskii V.N. (2005) Extended thermodynamics in a discrete-system approach, Eur. J. Phys. т. 26, 769–781.
- ^ Pokrovskii, Vladimir N. (2013). "A Derivation of the Main Relations of Nonequilibrium Thermodynamics". ISRN Thermodynamics. 2013: 1–9. Дои:10.1155/2013/906136.
- ^ J. S. Dugdale (1996). Entropy and its Physical Meaning. Тейлор и Фрэнсис. п.13. ISBN 978-0-7484-0569-5.
This law is the basis of temperature.
- ^ Zemansky, M.W. (1968), pp. 207–209.
- ^ Куинн, Т. (1983), стр. 8.
- ^ "Concept and Statements of the Second Law". web.mit.edu. Получено 2010-10-07.
- ^ Либ и Ингвасон (1999).
- ^ Рао (2004), п. 213.
- ^ Карно, С. (1824/1986).
- ^ Карно, С. (1824/1986), стр. 51.
- ^ Карно, С. (1824/1986), стр. 46.
- ^ Карно, С. (1824/1986), стр. 68.
- ^ Трусделл, К. (1980), Глава 5.
- ^ Адкинс, С.Дж. (1968/1983), стр. 56–58.
- ^ Мюнстер, А. (1970), стр. 11.
- ^ Кондепуди, Д., Пригожин, И. (1998), стр.67–75.
- ^ Лебон, Г., Джоу, Д., Касас-Васкес, Дж. (2008), стр. 10.
- ^ Eu, B.C. (2002), стр. 32–35.
- ^ Клаузиус (1850).
- ^ Клаузиус (1854 г.), п. 86.
- ^ Томсон (1851).
- ^ Планк, М. (1897/1903), стр. 86.
- ^ Робертс, Дж. К., Миллер, А. (1928/1960), стр. 319.
- ^ тер Хаар, Д., Вергеланд, Х. (1966), стр. 17.
- ^ Рао, Ю. В. С. (1997). Химическая инженерия термодинамика. Университеты Press. п. 158. ISBN 978-81-7371-048-3.
- ^ Планк, М. (1897/1903), стр. 100.
- ^ Планк, М. (1926), стр. 463, перевод Уффинка Дж. (2003), стр. 131.
- ^ Робертс, Дж. К., Миллер, А. (1928/1960), стр. 382. Этот источник частично дословно взят из заявления Планка, но он не цитирует его. Этот источник называет утверждение принципом увеличения энтропии.
- ^ Уленбек, Г., Форд, Г. (1963), стр. 16.
- ^ Каратеодори, К. (1909).
- ^ Бухдаль, Х.А. (1966), стр. 68.
- ^ Сычев В. В. (1991). Дифференциальные уравнения термодинамики.. Тейлор и Фрэнсис. ISBN 978-1-56032-121-7.
- ^ а б Либ и Ингвасон (1999), п. 49.
- ^ а б Планк, М. (1926).
- ^ Бухдаль, Х.А. (1966), стр. 69.
- ^ Уффинк, Дж. (2003), стр. 129–132.
- ^ Трусделл, К., Манкастер, Р. (1980). Основы кинетической теории Максвелла простого одноатомного газа, рассматриваемой как раздел рациональной механики, Academic Press, Нью-Йорк, ISBN 0-12-701350-4, п. 15.
- ^ Планк, М. (1897/1903), стр. 81.
- ^ Планк, М. (1926), стр. 457, перевод редактора Википедии.
- ^ Либ, Э.Х., Ингвасон, Дж. (2003), стр. 149.
- ^ Borgnakke, C., Sonntag., R.E. (2009), стр. 304.
- ^ van Gool, W .; Bruggink, J.J.C. (Редакторы) (1985). Энергия и время в экономических и физических науках. Северная Голландия. С. 41–56. ISBN 978-0-444-87748-2.CS1 maint: дополнительный текст: список авторов (связь)
- ^ Граббстрем, Роберт В. (2007). «Попытка ввести динамику в общие соображения эксергии». Прикладная энергия. 84 (7–8): 701–718. Дои:10.1016 / j.apenergy.2007.01.003.
- ^ Теорема Клаузиуса в Wolfram Research
- ^ Денби, К.Г., Денби, Дж. (1985). Энтропия по отношению к неполному знанию, Издательство Кембриджского университета, Кембридж, Великобритания, ISBN 0-521-25677-1С. 43–44.
- ^ Гранди, W.T., младший (2008). Энтропия и эволюция макроскопических систем во времени, Oxford University Press, Оксфорд, ISBN 978-0-19-954617-6С. 55–58.
- ^ Энтропийные сайты - Руководство Контент выбран Фрэнк Л. Ламберт
- ^ Клаузиус (1867).
- ^ Генис, Балаш (2017). «Максвелл и нормальное распределение: цветная история о вероятности, независимости и тенденции к равновесию». Исследования по истории и философии современной физики. 57: 53–65. arXiv:1702.01411. Bibcode:2017ШПМП..57 ... 53Г. Дои:10.1016 / j.shpsb.2017.01.001. S2CID 38272381.
- ^ Хокинг, SW (1985). «Стрела времени в космологии». Phys. Ред. D. 32 (10): 2489–2495. Bibcode:1985ПхРвД..32.2489Н. Дои:10.1103 / PhysRevD.32.2489. PMID 9956019.
- ^ Грин, Брайан (2004). Ткань космоса. Альфред А. Кнопф. п.171. ISBN 978-0-375-41288-2.
- ^ Лебовиц, Джоэл Л. (сентябрь 1993 г.). «Энтропия Больцмана и стрела времени» (PDF). Физика сегодня. 46 (9): 32–38. Bibcode:1993ФТ .... 46и..32Л. Дои:10.1063/1.881363. Получено 2013-02-22.
- ^ Кэрролл, С. (2017). Общая картина: о происхождении жизни, смысле и самой Вселенной. Пингвин.
- ^ Грин, Б. (2004). Ткань космоса: пространство, время и фактура реальности. Кнопф.
- ^ Дэвис, П. С. (1983). Инфляция и временная асимметрия во Вселенной. Природа, 301 (5899), 398-400.
- ^ Физики обсуждают идею Хокинга о том, что у Вселенной не было начала. Wolchover, N. Quantmagazine, 6 июня 2019 г. Дата обращения: 28 ноября 2020 г.
- ^ Леон Бриллюэн Наука и теория информации (Academic Press, 1962) (Дувр, 2004)
- ^ Ladyman, J .; Lambert, J .; Вайснер, К. Что такое сложная система? Евро. J. Philos. Sci. 2013, 3,33–67.
- ^ Эспозито М., Линденберг К. и Ван ден Брок К. (2010). Производство энтропии как взаимосвязь между системой и резервуаром. Новый журнал физики, 12 (1), 013013.
- ^ Баэз, Джон (7 августа 2000 г.). "Может ли гравитация уменьшить энтропию?". Отделение математики Калифорнийского университета в Риверсайде. Калифорнийский университет в Риверсайде. Получено 7 июн 2020.
... гравитационно связанный шар газа имеет отрицательную теплоемкость!
- ^ а б Гранди, W.T. (младший) (2008), стр. 151.
- ^ Каллен, Х. (1960/1985), стр. 15.
- ^ Либ, Э.Х., Ингвасон, Дж. (2003), стр. 190.
- ^ Дьярмати, И. (1967/1970), стр. 4-14.
- ^ Глансдорф П., Пригожин И. (1971).
- ^ Мюллер, И. (1985).
- ^ Мюллер, И. (2003).
- ^ Каллендер, Крейг (29 июля 2011 г.). «Термодинамическая асимметрия во времени». Стэнфордская энциклопедия философии.
- ^ Halliwell, J.J .; и другие. (1994). Физические истоки асимметрии времени. Кембридж. ISBN 978-0-521-56837-1. Глава 6
- ^ Шредингер, Э. (1950), стр. 192.
Источники
- Адкинс, Си-Джей (1968/1983). Равновесная термодинамика, (1-е издание 1968 г.), 3-е издание 1983 г., Cambridge University Press, Cambridge UK, ISBN 0-521-25445-0.
- Аткинс, П., де Паула, Дж. (2006). Физическая химия Аткинса, восьмое издание, W.H. Фриман, Нью-Йорк, ISBN 978-0-7167-8759-4.
- Аттард, П. (2012). Неравновесная термодинамика и статистическая механика: основы и приложения, Oxford University Press, Oxford UK, ISBN 978-0-19-966276-0.
- Байерлейн, Р. (1999). Теплофизика, Издательство Кембриджского университета, Кембридж, Великобритания, ISBN 0-521-59082-5.
- Байлын, М. (1994). Обзор термодинамики, Американский институт физики, Нью-Йорк, ISBN 0-88318-797-3.
- Бланделл, Стивен Дж.; Бланделл, Кэтрин М. (2010). Концепции теплофизики (2-е изд.). Оксфорд: Oxford University Press. Дои:10.1093 / acprof: oso / 9780199562091.001.0001. ISBN 9780199562107. OCLC 607907330.
- Больцманн, Л. (1896/1964). Лекции по теории газа, переведенный С.Г. Браш, Калифорнийский университет Press, Беркли.
- Borgnakke, C., Sonntag., R.E. (2009). Основы термодинамики, седьмое издание, Wiley, ISBN 978-0-470-04192-5.
- Бухдаль, Х.А. (1966). Концепции классической термодинамики, Издательство Кембриджского университета, Кембридж, Великобритания.
- Бриджмен, П.В. (1943). Природа термодинамики, Издательство Гарвардского университета, Кембридж, Массачусетс.
- Каллен, Х. (1960/1985). Термодинамика и введение в термостатистику(1-е издание 1960 г.) 2-е издание 1985 г., Вили, Нью-Йорк, ISBN 0-471-86256-8.
- К. Каратеодори (1909). "Untersuchungen über die Grundlagen der Thermodynamik". Mathematische Annalen. 67 (3): 355–386. Дои:10.1007 / bf01450409. S2CID 118230148.
Аксиома II: In Jeder Bellebigen Umgebung eines willkürlich vorgeschriebenen Anfangszustandes gibt es Zustände, die durch adiabatische Zustandsänderungen nicht trustbig приближенно верден кённен. (стр.363)
. Перевод можно найти здесь. Также в основном надежный перевод должен быть найден в Kestin, J. (1976). Второй закон термодинамики, Дауден, Хатчинсон и Росс, Страудсбург, Пенсильвания. - Карно, С. (1824/1986). Размышления о движущей силе огня, Издательство Манчестерского университета, Манчестер Великобритания, ISBN 0-7190-1741-6. Также здесь.
- Чепмен, С., Каулинг, Т. (1939/1970). Математическая теория неоднородных газов. Учет кинетической теории вязкости, теплопроводности и диффузии в газах, третье издание 1970 г., Cambridge University Press, Лондон.
- Клаузиус, Р. (1850). "Ueber Die Bewegende Kraft Der Wärme Und Die Gesetze, Welche Sich Daraus Für Die Wärmelehre Selbst Ableiten Lassen". Annalen der Physik. 79 (4): 368–397, 500–524. Bibcode:1850АнП ... 155..500С. Дои:10.1002 / andp.18501550403. HDL:2027 / uc1. $ B242250. Получено 26 июн 2012. Переведено на английский язык: Клаузиус, Р. (июль 1851 г.). «О движущейся силе тепла и законах, относящихся к самой природе тепла, которые выводятся из этого». Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал. 4-й. 2 (VIII): 1–21, 102–119. Дои:10.1080/14786445108646819. Получено 26 июн 2012.
- Клаузиус, Р. (1854). "Über eine veränderte Form des zweiten Hauptsatzes der Mechanischen Wärmetheorie" (PDF). Annalen der Physik. xciii (12): 481–506. Bibcode:1854AnP ... 169..481C. Дои:10.1002 / andp.18541691202. Получено 24 марта 2014. Переведено на английский язык: Клаузиус, Р. (июль 1856 г.). "Об одной модификации второй основной теоремы механической теории тепла". Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал. 4-й. 2: 86. Получено 24 марта 2014. Печатается на: Клаузиус, Р. (1867). Механическая теория тепла - в ее приложениях к паровому двигателю и физическим свойствам тел. Лондон: Джон ван Ворст. Получено 19 июн 2012.
редакции: PwR_Sbkwa8IC.
- Денби, К. (1954/1981). Принципы химического равновесия. С приложениями в химии и химической инженерии, четвертое издание, Cambridge University Press, Кембридж, Великобритания, ISBN 0-521-23682-7.
- Eu, B.C. (2002). Обобщенная термодинамика. Термодинамика необратимых процессов и обобщенная гидродинамика., Kluwer Academic Publishers, Дордрехт, ISBN 1-4020-0788-4.
- Гиббс, Дж. (1876/1878). О равновесии разнородных веществ, Пер. Conn. Acad., 3: 108–248, 343–524, перепечатано в Собрание сочинений Дж. Уилларда Гиббса, доктора философии, LL. Д., под редакцией W.R. Longley, R.G. Van Name, Longmans, Green & Co., Нью-Йорк, 1928, том 1, стр. 55–353.
- Грием, Х.Р. (2005). Принципы плазменной спектроскопии (Кембриджские монографии по физике плазмы), Издательство Кембриджского университета, Нью-Йорк ISBN 0-521-61941-6.
- Глансдорф П., Пригожин И. (1971). Термодинамическая теория структуры, устойчивости и флуктуаций, Wiley-Interscience, Лондон, 1971 г., ISBN 0-471-30280-5.
- Гранди, W.T., младший (2008). Энтропия и эволюция макроскопических систем во времени. Издательство Оксфордского университета. ISBN 978-0-19-954617-6.
- Гревен, А., Келлер, Г., Варнеке (редакторы) (2003). Энтропия, Princeton University Press, Принстон, штат Нью-Джерси, ISBN 0-691-11338-6.
- Гуггенхайм, Э.А. (1949). «Статистические основы термодинамики», Исследование, 2: 450–454.
- Гуггенхайм, Э.А. (1967). Термодинамика. Передовое лечение для химиков и физиков, пятое исправленное издание, Северная Голландия, Амстердам.
- Дьярмати И. (1967/1970) Неравновесная термодинамика. Теория поля и вариационные принципы, перевод Э. Дьярмати и В.Ф. Хайнц, Спрингер, Нью-Йорк.
- Киттель, К., Кремер, Х. (1969/1980). Теплофизика, второе издание, Фриман, Сан-Франциско, Калифорния, ISBN 0-7167-1088-9.
- Кондепуди, Д., Пригожин, И. (1998). Современная термодинамика: от тепловых двигателей к диссипативным структурам, John Wiley & Sons, Чичестер, ISBN 0-471-97393-9.
- Лебон, Г., Джоу, Д., Касас-Васкес, Дж. (2008). Понимание неравновесной термодинамики: основы, приложения, границы, Springer-Verlag, Берлин, ISBN 978-3-540-74252-4.
- Lieb, E.H .; Ингвасон, Дж. (1999). «Физико-математические аспекты второго начала термодинамики». Отчеты по физике. 310 (1): 1–96. arXiv:cond-mat / 9708200. Bibcode:1999ФР ... 310 .... 1л. Дои:10.1016 / S0370-1573 (98) 00082-9. S2CID 119620408.
- Либ, Э. Х., Ингвасон, Дж. (2003). Энтропия классической термодинамики, стр. 147–195, глава 8 Энтропия, Гревен, А., Келлер, Г., Варнеке (редакторы) (2003).
- Мандл, Ф. (1988). Статистическая физика (второе изд.). Wiley & Sons. ISBN 978-0-471-91533-1.
- Максвелл, Дж. (1867 г.). «К динамической теории газов». Фил. Пер. R. Soc. Лондон. 157: 49–88. Дои:10.1098 / рстл.1867.0004. S2CID 96568430.
- Мюллер, И. (1985). Термодинамика, Питман, Лондон, ISBN 0-273-08577-8.
- Мюллер, И. (2003). Энтропия в неравновесии, стр. 79–109, глава 5 Энтропия, Гревен, А., Келлер, Г., Варнеке (редакторы) (2003).
- Мюнстер, А. (1970), Классическая термодинамика, перевод Е.С. Хальберштадт, Wiley – Interscience, Лондон, ISBN 0-471-62430-6.
- Пиппард, А. (1957/1966). Элементы классической термодинамики для продвинутых студентов-физиков, оригинальная публикация 1957 г., переиздание 1966 г., Cambridge University Press, Cambridge UK.
- Планк, М. (1897/1903). Трактат по термодинамике, перевод A. Ogg, Longmans Green, London, p. 100.
- Планк. М. (1914). Теория теплового излучения, перевод Мазиуса, М. второго немецкого издания, Сын П. Блэкистона и Ко, Филадельфия.
- Планк, М. (1926). Über die Begründung des zweiten Hauptsatzes der Thermodynamik, Sitzungsberichte der Preussischen Akademie der Wissenschaften: Physikalisch-Mathematische Klasse: 453–463.
- Покровский В.Н. (2005) Расширенная термодинамика в дискретно-системном подходе, Eur. J. Phys. т. 26, 769–781.
- Покровский, Владимир Н. (2013). «Вывод основных соотношений неравновесной термодинамики». ISRN Термодинамика. 2013: 1–9. Дои:10.1155/2013/906136.
- Куинн, Т. (1983). Температура, Academic Press, Лондон, ISBN 0-12-569680-9.
- Рао, Y.V.C. (2004). Введение в термодинамику. Университеты Press. п. 213. ISBN 978-81-7371-461-0.
- Робертс, Дж. К., Миллер, А. (1928/1960). Тепло и термодинамика, (первое издание 1928 г.), пятое издание, Blackie & Son Limited, Глазго.
- Шредингер, Э. (1950). Необратимость, Proc. R. Ir. Акад., A53: 189–195.
- тер Хаар, Д., Вергеланд, Х. (1966). Элементы термодинамики, Издательство Addison-Wesley Publishing, Ридинг, Массачусетс.
- Томсон, В. (1851). «О динамической теории тепла с численными результатами, выведенными из эквивалента тепловой единицы Джоуля, и наблюдений М. Реньо над паром». Сделки Королевского общества Эдинбурга. XX (часть II): 261–268, 289–298. Также опубликовано в Томсон, В. (декабрь 1852 г.). «О динамической теории тепла с численными результатами, выведенными из эквивалента тепловой единицы Джоуля, и наблюдений М. Реньо над паром». Филос. Mag. 4. IV (22): 13. Получено 25 июн 2012.
- Томсон, В. (1852). Об универсальной тенденции природы к рассеиванию механической энергии Философский журнал, сер. 4, стр. 304.
- Тиса, Л. (1966). Обобщенная термодинамика, M.I.T Press, Cambridge MA.
- Трусделл, К. (1980). Трагикомическая история термодинамики 1822–1854 гг., Спрингер, Нью-Йорк, ISBN 0-387-90403-4.
- Уффинк, Дж. (2001). Обманите свой путь вторым законом термодинамики, Stud. Hist. Фил. Мод. Phys., 32(3): 305–394.
- Уффинк, Дж. (2003). Необратимость и второй закон термодинамики, глава 7 Энтропия, Гревен, А., Келлер, Г., Варнеке (редакторы) (2003), Princeton University Press, Princeton NJ, ISBN 0-691-11338-6.
- Уленбек, Г., Форд, Г. (1963). Лекции по статистической механике, Американское математическое общество, Providence RI.
- Земанский, М. (1968). Тепло и термодинамика. Учебник для среднего уровня, пятое издание, McGraw-Hill Book Company, Нью-Йорк.
дальнейшее чтение
- Гольдштейн, Мартин и Инге Ф., 1993. Холодильник и Вселенная. Harvard Univ. Нажмите. Гл. 4–9 содержат введение во Второй закон, немного менее техническое, чем эта статья. ISBN 978-0-674-75324-2
- Лефф, Харви С. и Рекс, Эндрю Ф. (ред.) 2003. Демон Максвелла 2: энтропия, классическая и квантовая информация, вычисления. Бристоль Великобритания; Филадельфия, штат Пенсильвания: Институт Физики. ISBN 978-0-585-49237-7
- Холливелл, Дж. Дж. (1994). Физические истоки асимметрии времени. Кембридж. ISBN 978-0-521-56837-1.(технический).
- Карно, Сади (1890). Терстон, Роберт Генри (ред.). Размышления о движущей силе тепла и машинах, способных развивать эту силу. Нью-Йорк: J. Wiley & Sons. (полный текст 1897 г. изд.) (html)
- Стивен Джей Клайн (1999). Об энтропии и интерпретирующей термодинамике., Ла Каньяда, Калифорния: DCW Industries. ISBN 1-928729-01-0.
- Костич, М (2011). Пересмотр второго закона деградации энергии и генерации энтропии: от гениального рассуждения Сади Карно до целостного обобщения. AIP Conf. Proc. Материалы конференции AIP. 1411. С. 327–350. Bibcode:2011AIPC.1411..327K. CiteSeerX 10.1.1.405.1945. Дои:10.1063/1.3665247. ISBN 978-0-7354-0985-9. также в [1].
внешняя ссылка
- Стэнфордская энциклопедия философии: "Философия статистической механики"- Лоуренс Скляр.
- Второй закон термодинамики в курсе MIT Единая термодинамика и движение от проф. З. С. Спаковского
- E.T. Джейнс, 1988, "Эволюция принципа Карно, "в Дж. Дж. Эриксон и К. Р. Смит (ред.)Максимум энтропии и байесовские методы в науке и технике, Vol. 1: стр. 267.
- Каратеодори, К., "Исследование основ термодинамики", пер. Д. Х. Дельфених
- Второй закон термодинамики, Обсуждение BBC Radio 4 с Джоном Гриббином, Питером Аткинсом и Моникой Грейди (В наше время, 16 декабря 2004 г.)
- Энтропия (журнал), 2004
- Журнал Международного общества истории философии науки, 2012 г.
































































![S = k _ { mathrm B} ln left [ Omega left (E right) right] ,](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb924dffe4f5c2c580cd40461cf5bfc5159ac881)






![frac {1} {k _ { mathrm B} T} Equiv beta Equiv frac {d ln left [ Omega left (E right) right]} {dE}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e720432da60639a2f9cdcefb4ac56845da4f36b0)

























