WikiDer > Принцип неопределенности
В квантовая механика, то принцип неопределенности (также известен как Принцип неопределенности Гейзенберга) является любым из множества математические неравенства[1] утверждая фундаментальный предел точности, с которой значения некоторых пар физических величин частица, Такие как позиция, Икс, и импульс, п, можно предсказать из первоначальные условия.
Такие пары переменных известны как дополнительные переменные или канонически сопряженные переменные; и, в зависимости от интерпретации, принцип неопределенности ограничивает, в какой степени такие сопряженные свойства сохраняют свое приблизительное значение, поскольку математическая структура квантовой физики не поддерживает понятие одновременно четко определенных сопряженных свойств, выражаемых одним значением. Принцип неопределенности подразумевает, что, как правило, невозможно предсказать значение величины с произвольной уверенностью, даже если указаны все начальные условия.
Впервые введено в 1927 году немецким физиком Вернер Гейзенберг, принцип неопределенности гласит, что чем точнее определяется положение некоторой частицы, тем менее точно ее импульс можно предсказать из начальных условий, и наоборот.[2] Формальное неравенство, связывающее стандартное отклонение позиции σИкс и стандартное отклонение импульса σп был получен Эрл Гессен Кеннард[3] позже в том же году и Герман Вейль[4] в 1928 г .:
куда час это приведенная постоянная Планка, час/ (2π).
Исторически принцип неопределенности путали.[5][6] со связанным эффектом в физика, называется эффект наблюдателя, в котором отмечается, что измерения некоторых систем не могут быть выполнены без воздействия на систему, то есть без изменения чего-либо в системе. Гейзенберг использовал такой эффект наблюдателя на квантовом уровне (см. Ниже) как физическое «объяснение» квантовой неопределенности.[7] Однако с тех пор стало яснее, что принцип неопределенности присущ всем свойствам. волновые системы,[8] и что он возникает в квантовой механике просто из-за волна материи природа всех квантовых объектов. Таким образом, принцип неопределенности фактически утверждает фундаментальное свойство квантовых систем и не является утверждением об успехе современных технологий в наблюдениях..[9] Следует подчеркнуть, что измерение означает не только процесс, в котором участвует физик-наблюдатель, но скорее любое взаимодействие между классическими и квантовыми объектами независимо от любого наблюдателя.[10][примечание 1] [заметка 2]
Поскольку принцип неопределенности является таким основным результатом в квантовой механике, типичные эксперименты в квантовой механике обычно наблюдают его аспекты. Некоторые эксперименты, однако, могут намеренно проверять конкретную форму принципа неопределенности как часть своей основной исследовательской программы. К ним относятся, например, тесты соотношений неопределенностей число – фаза в сверхпроводящий[12] или же квантовая оптика[13] системы. Приложения, зависящие от принципа неопределенности их работы, включают в себя технологию с чрезвычайно низким уровнем шума, такую как требуемая в гравитационно-волновые интерферометры.[14]
Вступление


Принцип неопределенности не так очевиден на макроскопических масштабах повседневного опыта.[15] Поэтому полезно продемонстрировать, как это применимо к более понятным физическим ситуациям. Две альтернативные концепции квантовой физики предлагают разные объяснения принципа неопределенности. В волновая механика картина принципа неопределенности визуально нагляднее, но тем более абстрактна матричная механика picture формулирует его таким образом, чтобы его было легче обобщить.
Математически в волновой механике соотношение неопределенности между положением и импульсом возникает из-за того, что выражения волновой функции в двух соответствующих ортонормированный базы в Гильбертово пространство находятся Преобразования Фурье друг друга (т. е. позиция и импульс равны сопряженные переменные). Ненулевая функция и ее преобразование Фурье не могут быть точно локализованы одновременно. Подобный компромисс между дисперсиями сопряженных Фурье возникает во всех системах, основанных на анализе Фурье, например, в звуковых волнах: чистый тон - это острый шип на одной частоте, в то время как его преобразование Фурье дает форму звуковой волны во временной области, которая является полностью делокализованной синусоидальной волной. В квантовой механике два ключевых момента заключаются в том, что положение частицы принимает форму волна материи, а импульс - его сопряженная с Фурье функция, обеспечиваемая соотношением де Бройля п = ħk, куда k это волновое число.
В матричная механика, то математическая формулировка квантовой механики, любая пара не-поездка на работу самосопряженные операторы представляющий наблюдаемые подвержены аналогичным пределам неопределенности. Собственное состояние наблюдаемого представляет состояние волновой функции для определенного значения измерения (собственное значение). Например, если измерение наблюдаемого А выполняется, то система находится в определенном собственном состоянии Ψ этого наблюдаемого. Однако частное собственное состояние наблюдаемого А не обязательно быть собственным состоянием другой наблюдаемой B: Если да, то для него нет единственного связанного измерения, поскольку система не находится в собственном состоянии этой наблюдаемой.[16]
Интерпретация волновой механики
(Ссылка [10])
Согласно гипотеза де Бройля, каждый объект во Вселенной - это волна, т.е. ситуация, порождающая это явление. Положение частицы описывается волновая функция . Не зависящая от времени волновая функция одномодовой плоской волны волнового числа k0 или импульс п0 является
В Родившееся правило заявляет, что это следует интерпретировать как функция амплитуды плотности вероятности в том смысле, что вероятность найти частицу между а и б является
В случае одномодовой плоской волны это равномерное распределение. Другими словами, положение частицы крайне неопределенно в том смысле, что она может находиться практически в любом месте волнового пакета.
С другой стороны, рассмотрим волновую функцию, которая является сумма многих волн, что мы можем записать как
куда Ап представляет собой относительный вклад моды пп к общей сумме. На рисунках справа показано, как при добавлении множества плоских волн волновой пакет может стать более локализованным. Мы можем сделать еще один шаг к континуальному пределу, когда волновая функция является интеграл по всем возможным режимам
с представляет собой амплитуду этих мод и называется волновой функцией в импульсное пространство. В математических терминах мы говорим, что это преобразование Фурье из и это Икс и п находятся сопряженные переменные. Сложение всех этих плоских волн обходится дорого, а именно: импульс стал менее точным, поскольку он стал смесью волн с множеством разных импульсов.
Одним из способов количественной оценки точности положения и импульса является стандартное отклонение σ. С является функцией плотности вероятности для положения, мы вычисляем ее стандартное отклонение.
Повышается точность положения, т.е. уменьшается σИкс, используя много плоских волн, тем самым ослабляя точность импульса, т.е. увеличивая σп. Другими словами, σИкс и σп есть Обратная зависимость или хотя бы ограничены снизу. Это принцип неопределенности, точным пределом которого является граница Кеннарда. Щелкните значок Показать Нажмите кнопку ниже, чтобы увидеть полуформальный вывод неравенства Кеннарда с использованием волновой механики.
| Доказательство неравенства Кеннарда с помощью волновой механики |
|---|
| Мы заинтересованы в отклонения позиции и импульса, определяемого как Не теряя общий смысл, будем считать, что средства исчезают, что равносильно смещению начала координат. (Более общее доказательство, которое не делает этого предположения, приводится ниже.) Это дает нам более простую форму Функция можно интерпретировать как вектор в функциональное пространство. Мы можем определить внутренний продукт для пары функций ты(Икс) и v(Икс) в этом векторном пространстве: где звездочка обозначает комплексно сопряженный. Определив этот внутренний продукт, отметим, что дисперсию для позиции можно записать как Мы можем повторить это для импульса, интерпретируя функцию как вектор, но мы также можем воспользоваться тем фактом, что и являются преобразованиями Фурье друг друга. Мы оцениваем обратное преобразование Фурье через интеграция по частям: где сокращенный член обращается в нуль, поскольку волновая функция обращается в нуль на бесконечности. Часто термин называется оператором импульса в позиционном пространстве. Применение Теорема Парсеваля, мы видим, что дисперсию импульса можно записать как В Неравенство Коши – Шварца утверждает, что Квадрат модуля любого комплексного числа z можно выразить как мы позволяем и и подставьте их в уравнение выше, чтобы получить Остается только оценить эти внутренние продукты. Вставляя это в приведенные выше неравенства, мы получаем или извлечение квадратного корня Обратите внимание, что единственный физика участие в этом доказательстве было то, что и - волновые функции для положения и импульса, которые являются преобразованиями Фурье друг друга. Аналогичный результат будет иметь место для любой пара сопряженных переменных. |
Интерпретация матричной механики
(Ссылка [10])
В матричной механике наблюдаемые, такие как положение и импульс, представлены как самосопряженные операторы. При рассмотрении пар наблюдаемых важной величиной является величина коммутатор. Для пары операторов Â и B̂, их коммутатор определяется как
В случае положения и импульса коммутатор - это каноническое коммутационное соотношение
Физический смысл некоммутативности можно понять, рассмотрев влияние коммутатора на положение и импульс. собственные состояния. Позволять - правое собственное состояние позиции с постоянным собственным значением Икс0. По определению это означает, что Применяя коммутатор к дает
куда Я это оператор идентификации.
Допустим, ради доказательство от противного, который также является правым собственным состоянием импульса с постоянным собственным значением п0. Если бы это было правдой, то можно было бы написать
С другой стороны, указанное выше каноническое коммутационное соотношение требует, чтобы
Это означает, что никакое квантовое состояние не может быть одновременно и положением, и собственным состоянием импульса.
Когда состояние измеряется, оно проецируется на собственное состояние на основе соответствующей наблюдаемой. Например, если измеряется положение частицы, то состояние равно собственному состоянию положения. Это означает, что состояние нет это собственное состояние импульса, а, скорее, его можно представить как сумму нескольких базисных собственных состояний импульса. Другими словами, импульс должен быть менее точным. Эта точность может быть определена количественно Стандартное отклонение,
Как и в вышеприведенной интерпретации волновой механики, можно увидеть компромисс между соответствующими точностями этих двух факторов, количественно определяемый принципом неопределенности.
Предел Гейзенберга
В квантовая метрология, и особенно интерферометрия, то Предел Гейзенберга - это оптимальная скорость, с которой точность измерения может масштабироваться в зависимости от энергии, используемой при измерении. Обычно это измерение фазы (применяется к одному плечу Разделитель луча), а энергия определяется количеством фотонов, используемых в интерферометр. Хотя некоторые утверждают, что нарушили предел Гейзенберга, это отражает разногласия по поводу определения ресурса масштабирования.[17] Определенный подходящим образом, предел Гейзенберга является следствием основных принципов квантовой механики и его нельзя превзойти, хотя слабый предел Гейзенберга можно преодолеть.[18]
Соотношения неопределенностей Робертсона – Шредингера
Наиболее распространенной общей формой принципа неопределенности является Робертсон отношение неопределенности.[19]
Для произвольного Эрмитов оператор мы можем связать стандартное отклонение
где скобки указать ожидаемое значение. Для пары операторов и , мы можем определить их коммутатор в качестве
В этих обозначениях соотношение неопределенностей Робертсона дается выражением
Соотношение неопределенностей Робертсона немедленно следует из немного более сильное неравенство, Соотношение неопределенностей Шредингера,[20]
где мы ввели антикоммутатор,
| Доказательство соотношения неопределенностей Шредингера | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Показанный здесь вывод включает и основывается на выводах, показанных Робертсоном,[19] Шредингер[20] и стандартные учебники, такие как Гриффитс.[21] Для любого эрмитова оператора , исходя из определения отклонение, у нас есть мы позволяем и поэтому Аналогично для любого другого эрмитова оператора в том же состоянии за Таким образом, произведение двух отклонений может быть выражено как
Чтобы связать два вектора и , мы используем Неравенство Коши – Шварца[22] который определяется как и, таким образом, уравнение. (1) можно записать как
С в общем случае комплексное число, мы используем тот факт, что квадрат модуля любого комплексного числа определяется как , куда является комплексным сопряжением . Квадрат модуля также может быть выражен как
мы позволяем и и подставьте их в уравнение выше, чтобы получить
Внутренний продукт явно записывается как и используя тот факт, что и - эрмитовы операторы, находим Аналогичным образом можно показать, что Таким образом, мы имеем и Теперь мы подставляем два приведенных выше уравнения обратно в уравнение. (4) и получить Подставляя вышеуказанное в формулу. (2) получаем соотношение неопределенностей Шредингера У этого доказательства есть проблема[23] связанные с доменами задействованных операторов. Чтобы доказательство имело смысл, вектор должен быть в сфере неограниченный оператор , что не всегда так. На самом деле соотношение неопределенностей Робертсона неверно, если переменная угла и - производная по этой переменной. В этом примере коммутатор является ненулевой константой, как и в соотношении неопределенностей Гейзенберга, и все же есть состояния, в которых произведение неопределенностей равно нулю.[24] (См. Раздел контрпример ниже.) Эту проблему можно решить, используя вариационный метод для доказательства.,[25][26] или работая с экспоненциальной версией канонических коммутационных соотношений.[24] Отметим, что в общей форме соотношения неопределенностей Робертсона – Шредингера нет необходимости предполагать, что операторы и находятся самосопряженные операторы. Достаточно предположить, что они просто симметричные операторы. (Различие между этими двумя понятиями обычно замалчивается в физической литературе, где термин Эрмитский используется для одного или обоих классов операторов. См. Главу 9 книги Холла[27] для подробного обсуждения этого важного, но технического различия.) |
Смешанные состояния
Соотношение неопределенностей Робертсона – Шредингера можно просто обобщить, чтобы описать смешанные государства.,
Соотношения неопределенностей Макконе – Пати
Соотношение неопределенностей Робертсона – Шредингера может быть тривиальным, если состояние системы выбрано как собственное состояние одной из наблюдаемых. Более сильные соотношения неопределенностей, доказанные Макконом и Пати, дают нетривиальные оценки суммы дисперсий для двух несовместимых наблюдаемых.[28] (Более ранние работы по отношениям неопределенностей, сформулированным как сумма дисперсий, включают, например, Ref. [29] благодаря Хуангу.) Для двух некоммутирующих наблюдаемых и первое более сильное соотношение неопределенности дается формулой
куда , , - нормированный вектор, ортогональный состоянию системы и следует выбрать знак сделать это реальное количество положительным числом.
Второе более сильное соотношение неопределенности дается выражением
куда состояние ортогонально .Форма означает, что правая часть нового отношения неопределенности отлична от нуля, если только является собственным состоянием . Можно отметить, что может быть собственным состоянием не являясь собственным состоянием или же . Однако когда является собственным состоянием одной из двух наблюдаемых, соотношение неопределенностей Гейзенберга – Шредингера становится тривиальным. Но нижняя граница в новом соотношении отлична от нуля, если только является собственным состоянием обоих.
Фазовое пространство
в формулировка фазового пространства В квантовой механике соотношение Робертсона – Шредингера следует из условия положительности вещественной функции «звезда-квадрат». Учитывая Функция Вигнера с звездный продукт ★ и функция ж, обычно верно следующее:[30]
Выбор , мы приходим к
Поскольку это условие положительности выполнено для все а, б, и c, то все собственные значения матрицы неотрицательны.
Тогда неотрицательные собственные значения подразумевают соответствующее условие неотрицательности детерминант,
или, явно, после алгебраических манипуляций,
Примеры
Поскольку соотношения Робертсона и Шредингера предназначены для общих операторов, эти соотношения могут применяться к любым двум наблюдаемым для получения конкретных соотношений неопределенности. Ниже приведены некоторые из наиболее распространенных взаимосвязей, встречающихся в литературе.
- Для положения и количества движения каноническое коммутационное соотношение следует неравенство Кеннарда сверху:
- Для двух ортогональных составляющих полный угловой момент оператор объекта:
- куда я, j, k различны, и Jя обозначает угловой момент вдоль Икся ось. Это соотношение подразумевает, что если все три компонента не обращаются в нуль вместе, только один компонент углового момента системы может быть определен с произвольной точностью, обычно компонент, параллельный внешнему (магнитному или электрическому) полю. Более того, для , Выбор , , в мультиплетах углового момента, ψ = |j, м〉, Ограничивает Инвариант Казимира (угловой момент в квадрате, ) снизу и, таким образом, дает полезные ограничения, такие как j(j + 1) ≥ м(м + 1), и поэтому j ≥ м, среди прочего.
- В нерелятивистской механике время занимает привилегированное положение. независимая переменная. Тем не менее в 1945 г. Л. И. Мандельштам и И. Э. Тамм получил нерелятивистский соотношение неопределенности времени и энергии, следующее.[31][32] Для квантовой системы в нестационарном состоянии ψ и наблюдаемый B представлен самосопряженным оператором , имеет место следующая формула:
- где σE - стандартное отклонение оператора энергии (гамильтониана) в состоянии ψ, σB обозначает стандартное отклонение B. Хотя второй фактор в левой части имеет размерность времени, он отличается от параметра времени, входящего в Уравнение Шредингера. Это продолжительность жизни государства ψ относительно наблюдаемого B: Другими словами, это временной интервал (Δт), после которого математическое ожидание заметно меняется.
- Неформальный, эвристический смысл принципа следующий: состояние, которое существует только в течение короткого времени, не может иметь определенной энергии. Чтобы иметь определенную энергию, частота состояния должна быть определена точно, а это требует, чтобы состояние оставалось на протяжении многих циклов, обратных требуемой точности. Например, в спектроскопия, возбужденные состояния имеют конечное время жизни. Согласно принципу неопределенности времени-энергии, они не имеют определенной энергии, и каждый раз, когда они распадаются, выделяемая ими энергия немного отличается. Средняя энергия исходящего фотона имеет максимум при теоретической энергии состояния, но распределение имеет конечную ширину, называемую естественная ширина линии. Быстро распадающиеся состояния имеют широкую ширину линии, а медленно распадающиеся состояния имеют узкую ширину линии.[33]
- Тот же эффект ширины линии также затрудняет указание масса покоя нестабильных, быстро распадающихся частиц в физика элементарных частиц. Чем быстрее частицы распадаются (чем короче время его жизни), тем менее определена его масса (чем больше у частицы ширина).
- Для количества электронов в сверхпроводник и фаза своего Параметр порядка Гинзбурга – Ландау[34][35]
Контрпример
Предположим, мы рассматриваем квантовую частица на кольце, где волновая функция зависит от угловой переменной , which we may take to lie in the interval . Define "position" and "momentum" operators и к
и
where we impose periodic boundary conditions on . Определение depends on our choice to have диапазон от 0 до . These operators satisfy the usual commutation relations for position and momentum operators, .[36]
Теперь позвольте be any of the eigenstates of , which are given by . These states are normalizable, unlike the eigenstates of the momentum operator on the line. Also the operator is bounded, since ranges over a bounded interval. Thus, in the state , the uncertainty of is zero and the uncertainty of is finite, so that
Although this result appears to violate the Robertson uncertainty principle, the paradox is resolved when we note that is not in the domain of the operator , since multiplication by disrupts the periodic boundary conditions imposed on .[24] Thus, the derivation of the Robertson relation, which requires и to be defined, does not apply. (These also furnish an example of operators satisfying the canonical commutation relations but not the Вейлевские отношения.[37])
For the usual position and momentum operators и on the real line, no such counterexamples can occur. Так долго как и are defined in the state , the Heisenberg uncertainty principle holds, even if fails to be in the domain of или из .[38]
Примеры
Quantum harmonic oscillator stationary states
Consider a one-dimensional quantum harmonic oscillator. It is possible to express the position and momentum operators in terms of the операторы создания и уничтожения:
Using the standard rules for creation and annihilation operators on the energy eigenstates,
то отклонения may be computed directly,
The product of these standard deviations is then
In particular, the above Kennard bound[3] is saturated for the основное состояние п=0, for which the probability density is just the нормальное распределение.
Quantum harmonic oscillators with Gaussian initial condition
In a quantum harmonic oscillator of characteristic angular frequency ω, place a state that is offset from the bottom of the potential by some displacement Икс0 в качестве
where Ω describes the width of the initial state but need not be the same as ω. Through integration over the propagator, we can solve for the full time-dependent solution. After many cancelations, the probability densities reduce to
where we have used the notation to denote a normal distribution of mean μ and variance σ2. Copying the variances above and applying тригонометрические тождества, we can write the product of the standard deviations as
От отношений
we can conclude the following: (the right most equality holds only when Ω = ω) .
Когерентные состояния
A coherent state is a right eigenstate of the annihilation operator,
- ,
which may be represented in terms of Fock states в качестве
In the picture where the coherent state is a massive particle in a quantum harmonic oscillator, the position and momentum operators may be expressed in terms of the annihilation operators in the same formulas above and used to calculate the variances,
Therefore, every coherent state saturates the Kennard bound
with position and momentum each contributing an amount in a "balanced" way. Более того, каждый squeezed coherent state also saturates the Kennard bound although the individual contributions of position and momentum need not be balanced in general.
Частица в коробке
Consider a particle in a one-dimensional box of length . В eigenfunctions in position and momentum space находятся
и
куда and we have used the de Broglie relation . The variances of и can be calculated explicitly:
The product of the standard deviations is therefore
Для всех , количество is greater than 1, so the uncertainty principle is never violated. For numerical concreteness, the smallest value occurs when , в таком случае
Constant momentum
Assume a particle initially has a импульсное пространство wave function described by a normal distribution around some constant momentum п0 в соответствии с
where we have introduced a reference scale , с describing the width of the distribution−−cf. обезразмеривание. If the state is allowed to evolve in free space, then the time-dependent momentum and position space wave functions are
С и , this can be interpreted as a particle moving along with constant momentum at arbitrarily high precision. On the other hand, the standard deviation of the position is
such that the uncertainty product can only increase with time as
Additional uncertainty relations
Systematic and statistical errors
The inequalities above focus on the statistical imprecision of observables as quantified by the standard deviation . Heisenberg's original version, however, was dealing with the систематическая ошибка, a disturbance of the quantum system produced by the measuring apparatus, i.e., an эффект наблюдателя.
Если мы позволим represent the error (i.e., неточность) of a measurement of an observable А и the disturbance produced on a subsequent measurement of the conjugate variable B by the former measurement of А, then the inequality proposed by Ozawa[6] — encompassing both systematic and statistical errors — holds:
Heisenberg's uncertainty principle, as originally described in the 1927 formulation, mentions only the first term of Ozawa inequality, regarding the систематическая ошибка. Using the notation above to describe the error/disturbance эффект sequential measurements (первый А, тогда B), it could be written as
The formal derivation of the Heisenberg relation is possible but far from intuitive. Это было нет proposed by Heisenberg, but formulated in a mathematically consistent way only in recent years.[39][40]Also, it must be stressed that the Heisenberg formulation is not taking into account the intrinsic statistical errors и . There is increasing experimental evidence[8][41][42][43] that the total quantum uncertainty cannot be described by the Heisenberg term alone, but requires the presence of all the three terms of the Ozawa inequality.
Using the same formalism,[1] it is also possible to introduce the other kind of physical situation, often confused with the previous one, namely the case of simultaneous measurements (А и B at the same time):
The two simultaneous measurements on А и B are necessarily[44] нерезкий или же слабый.
It is also possible to derive an uncertainty relation that, as the Ozawa's one, combines both the statistical and systematic error components, but keeps a form very close to the Heisenberg original inequality. By adding Robertson[1]
and Ozawa relations we obtain
The four terms can be written as:
Defining:
как неточность in the measured values of the variable А и
как resulting fluctuation in the conjugate variable B,Fujikawa[45] established an uncertainty relation similar to the Heisenberg original one, but valid both for systematic and statistical errors:
Quantum entropic uncertainty principle
For many distributions, the standard deviation is not a particularly natural way of quantifying the structure. Например, соотношения неопределенностей, в которых одна из наблюдаемых представляет собой угол, имеют мало физического смысла для флуктуаций, превышающих один период.[26][46][47][48] Другие примеры включают очень бимодальные распределения, или же унимодальные распределения с расходящейся дисперсией.
Решение, позволяющее преодолеть эти проблемы, - это неопределенность, основанная на энтропийная неопределенность вместо продукта отклонений. При формулировании многомировая интерпретация квантовой механики в 1957 г., Хью Эверетт III предположил более сильное расширение принципа неопределенности, основанное на энтропийной достоверности.[49] Эта гипотеза, также изученная Хиршманом[50] и доказано в 1975 году Бекнером[51] Иво Бялыницки-Бирула и Ежи Мыцельски[52] состоит в том, что для двух нормированных безразмерных преобразование Фурье пары f (а) и г (б) куда
- и
Шеннон информационные энтропии
и
подчиняются следующему ограничению:
где логарифмы могут быть в любом основании.
Функции распределения вероятностей, связанные с волновой функцией положения ψ (х) и импульсная волновая функция φ (х) имеют размерности, равные обратной длине и импульсу соответственно, но энтропии могут быть сделаны безразмерными с помощью
куда Икс0 и п0 - произвольно выбранные длина и импульс соответственно, что делает аргументы логарифмов безразмерными. Обратите внимание, что энтропии будут функциями этих выбранных параметров. Из-за Соотношение преобразования Фурье между волновой функцией положения ψ (х) и импульсная волновая функция φ(п), указанное выше ограничение для соответствующих энтропий можно записать как
куда час является Постоянная Планка.
В зависимости от выбора Икс0 п0 product, выражение можно записать по-разному. Если Икс0 п0 выбрано быть час, тогда
Если вместо этого Икс0 п0 выбрано быть час, тогда
Если Икс0 и п0 выбираются равными единице в любой системе единиц измерения, то
куда час интерпретируется как безразмерное число, равное значению постоянной Планка в выбранной системе единиц. Обратите внимание, что эти неравенства можно распространить на многомодовые квантовые состояния или волновые функции более чем в одном пространственном измерении.[53]
Принцип квантовой энтропийной неопределенности более строг, чем принцип неопределенности Гейзенберга. Из обратных логарифмических неравенств Соболева[54]
(эквивалентно, из того факта, что нормальные распределения максимизируют энтропию всех таких с заданной дисперсией), легко следует, что этот принцип энтропийной неопределенности сильнее, чем основанный на стандартных отклонениях, потому что
Другими словами, принцип неопределенности Гейзенберга является следствием квантового принципа энтропийной неопределенности, но не наоборот. Несколько замечаний по поводу этих неравенств. Во-первых, выбор база e является общепринятым в физике условием. В качестве альтернативы логарифм может быть с любым основанием при условии, что он согласован с обеими сторонами неравенства. Во-вторых, вспомним Энтропия Шеннона был использован, нет квант энтропия фон Неймана. Наконец, нормальное распределение насыщает неравенство, и это единственное распределение с таким свойством, потому что это распределение вероятностей максимальной энтропии среди тех, у кого фиксированная дисперсия (см. Вот для доказательства).
| Энтропийная неопределенность нормального распределения |
|---|
| Мы демонстрируем этот метод на основном состоянии QHO, которое, как обсуждалось выше, насыщает обычную неопределенность, основанную на стандартных отклонениях. Масштаб длины можно установить так, как вам удобно, поэтому мы назначаем Распределение вероятностей - нормальное распределение с энтропией Шеннона Совершенно аналогичный расчет проводится для импульсного распределения. Выбор стандартного импульса : Таким образом, энтропийная неопределенность является предельным значением. |
У измерительного устройства будет конечное разрешение, заданное дискретизацией его возможных выходных сигналов в ячейки с вероятностью попадания в одну из ячейок, заданных правилом Борна. Мы рассмотрим наиболее распространенную экспериментальную ситуацию, в которой бины имеют одинаковый размер. Позволять δx быть мерой пространственного разрешения. Мы берем нулевой интервал для центрирования около начала координат, возможно, с небольшим постоянным смещением. c. Вероятность попадания в j-й интервал ширины δx является
Чтобы учесть эту дискретизацию, мы можем определить энтропию Шеннона волновой функции для данного измерительного прибора как
Согласно приведенному выше определению, отношение энтропийной неопределенности имеет вид
Здесь отметим, что δx δp/час - типичный бесконечно малый объем фазового пространства, используемый при вычислении функция распределения. Неравенство также строгое и ненасыщенное. Усилия по улучшению этой границы являются активной областью исследований.
| Пример нормального распределения |
|---|
| Сначала мы продемонстрируем этот метод на основном состоянии QHO, которое, как обсуждалось выше, насыщает обычную неопределенность, основанную на стандартных отклонениях. Вероятность попадания в один из этих интервалов может быть выражена через функция ошибки. Вероятности импульса полностью аналогичны. Для простоты установим разрешения на так что вероятности уменьшаются до Энтропию Шеннона можно оценить численно. Энтропийная неопределенность действительно больше предельного значения. Обратите внимание, что, несмотря на оптимальный случай, неравенство не насыщается. |
| Пример функции Sinc |
|---|
| Примером унимодального распределения с бесконечной дисперсией является функция sinc. Если волновая функция является правильно нормированным равномерным распределением, то его преобразование Фурье является функцией sinc, что дает бесконечную дисперсию импульса, несмотря на централизованную форму. С другой стороны, энтропийная неопределенность конечна. Предположим для простоты, что пространственное разрешение - это просто измерение с двумя ячейками, δx = а, и что импульсное разрешение δp = час/а. Разделить равномерное пространственное распределение на две равные ячейки несложно. Устанавливаем смещение c = 1/2, так что два интервала охватывают распределение. Бины для импульса должны охватывать всю реальную линию. Как и в случае с пространственным распределением, мы можем применить смещение. Однако оказывается, что энтропия Шеннона минимизируется, когда нулевой интервал для импульса центрируется в начале координат. (Читателю предлагается попробовать добавить смещение.) Вероятность нахождения в пределах произвольного интервала импульса может быть выражена через интеграл синуса. Энтропию Шеннона можно оценить численно. Энтропийная неопределенность действительно больше предельного значения. |
Неравенство Ефимова по матрицам Паули
В 1976 г. Сергей П. Ефимов вывел неравенство, уточняющее соотношение Робертсона с помощью коммутаторов высокого порядка. [55] Его подход основан на Матрицы Паули. Позже В.В. Додонов использовал этот метод для вывода соотношений для нескольких наблюдаемых с помощью Алгебра Клиффорда. [56][57]
По словам Джеки, [25] неопределенность Робертсона действительна только тогда, когда коммутатор является C-числом. Метод Ефимова эффективен для переменных, имеющих коммутаторы высокого порядка - например, для оператора кинетической энергии и для координатного. Рассмотрим два оператора и которые имеют коммутатор :
Для сокращения формул воспользуемся оператором отклонений:
- ,
когда новые операторы имеют нулевое среднее отклонение. Чтобы использовать Матрицы Паули мы можем рассматривать оператора:
где 2 × 2 спиновые матрицы есть коммутаторы:
куда антисимметричный символ. Они действуют в пространстве вращения независимо от Матрицы Паули определяют Алгебра Клиффорда. Возьмем произвольные числа в операторе быть реальным.
Физический квадрат оператора равен:
куда является сопряженный оператор и коммутаторы и следующие:
Оператор положительно определен, что существенно для получения неравенства ниже. Принимая среднее значение по состоянию , получаем положительно определенную матрицу 2 × 2:
где употреблено понятие:
и аналогичный для операторов . Что касается коэффициентов произвольны в уравнении, получаем положительно определенная матрица 6×6. Критерий сильвестра говорит, что его ведущие основные несовершеннолетние неотрицательны. Неопределенность Робертсона следует от минор четвертой степени. Для усиления результата вычисляем определитель шестого порядка:
Равенство наблюдается только тогда, когда состояние является собственным состоянием оператора и то же самое для спиновых переменных:
- .
Найденное соотношение можно применить к оператору кинетической энергии а для оператора координаты :
В частности, равенство в формуле наблюдается для основного состояния осциллятора, а правая часть неопределенности Робертсона обращается в нуль:
- .
Физический смысл отношения становится более понятным, если разделить его на квадрат ненулевого среднего импульса, что даст:
куда - квадрат эффективного времени, в течение которого частица движется около средней траектории (масса частицы равна 1).
Метод применим к трем некоммутирующим операторам углового момента . Компилируем оператор:
Напомним, что операторы являются вспомогательными и между спиновыми переменными частицы нет связи. Таким образом, важны только их коммутативные свойства. Квадратный и усредненный оператор дает положительно определенную матрицу, откуда получаем следующее неравенство:
Для разработки метода для группы операторов можно использовать алгебру Клиффорда вместо матриц Паули. [57].
Гармонический анализ
В контексте гармонический анализ, раздел математики, принцип неопределенности подразумевает, что нельзя одновременно локализовать значение функции и ее преобразование Фурье. А именно, имеет место неравенство
Дополнительные неравенства математической неопределенности, включая указанные выше энтропийная неопределенность, удерживайте между функцией ж и его преобразование Фурье ƒ̂:[58][59][60]
Обработка сигналов
В контексте обработка сигналов, и в частности частотно-временной анализ, принципы неопределенности называются Предел Габора, после Деннис Габор, или иногда Предел Гейзенберга – Габора. Основной результат, который следует из «теоремы Бенедикса» ниже, состоит в том, что функция не может быть одновременно время ограничено и группа ограничена (функция и ее преобразование Фурье не могут иметь одновременно ограниченную область определения) - см. Bandlimited vs. timelimited. Таким образом
куда и - стандартные отклонения оценок времени и частоты соответственно.[61]
Иначе говоря, «Нельзя одновременно резко локализовать сигнал (функция ж ) как в область времени и частотная область (ƒ̂, его преобразование Фурье) ".
При применении к фильтрам результат означает, что нельзя одновременно достичь высокого временного и частотного разрешения; конкретным примером являются вопросы разрешения кратковременного преобразования Фурье- если используется широкое окно, хорошее разрешение по частоте достигается за счет временного разрешения, в то время как узкое окно имеет противоположный компромисс.
Альтернативные теоремы дают более точные количественные результаты, и в частотно-временном анализе, вместо того, чтобы интерпретировать (одномерные) временную и частотную области по отдельности, вместо этого предел интерпретируется как нижний предел для поддержки функции в (2 -мерная) частотно-временная плоскость. На практике предел Габора ограничивает одновременный частотно-временное разрешение достигается без помех; можно достичь более высокого разрешения, но за счет того, что различные компоненты сигнала будут мешать друг другу.
В результате, для анализа сигналов, в которых важны переходные процессы, вейвлет-преобразование часто используется вместо Фурье.
DFT-принцип неопределенности
Существует принцип неопределенности, который использует разреженность сигнала (или количество ненулевых коэффициентов).[62]
Позволять быть последовательностью N комплексные числа и это дискретное преобразование Фурье.
Обозначим через количество ненулевых элементов во временной последовательности и по количество ненулевых элементов в частотной последовательности . Потом,
Теорема Бенедикса
Амрейн-Бертье[63] и теорема Бенедикса[64] интуитивно говорит, что множество точек, где ж отлична от нуля и множество точек, где ƒ̂ не равно нулю, оба не могут быть маленькими.
В частности, для функции невозможно ж в L2(р) и его преобразование Фурье ƒ̂ чтобы оба были поддержанный на множествах конечных Мера Лебега. Более количественная версия[65][66]
Ожидается, что фактор CeC | S || Σ | может быть заменен на CeC(|S||Σ|)1/d, который известен, только если S или же Σ выпуклый.
Принцип неопределенности Харди
Математик Г. Х. Харди сформулировал следующий принцип неопределенности:[67] это невозможно для ж и ƒ̂ чтобы оба были «очень быстро убывающими». В частности, если ж в таково, что
и
- ( целое число),
тогда, если ab > 1, ж = 0, а если ab = 1, то существует многочлен п степени ≤ N такой, что
Позже это было улучшено следующим образом: если таково, что
тогда
куда п является многочленом степени (N − d)/2 и А настоящий d×d положительно определенная матрица.
Этот результат был сформулирован без доказательства в полных работах Бёрлинга и доказан в Хёрмандере.[68] (случай ) и Бонами, Деманж и Джеминг[69] для общего случая. Отметим, что из версии Хёрмандера – Бёрлинга следует случай ab > 1 в теореме Харди, а версия Бонами – Деманжа – Джейминга охватывает всю силу теоремы Харди. Другое доказательство теоремы Бёрлинга, основанное на теореме Лиувилля, появилось в [5].[70]
Полное описание кейса ab < 1 а также следующее расширение распределений классов Шварца появляется в исх.[71]
Теорема. Если умеренное распределение таково, что
и
тогда
для некоторого удобного многочлена п и вещественная положительно определенная матрица А типа d × d.
История
Вернер Гейзенберг сформулировал принцип неопределенности при Нильс Борв Копенгагене, работая над математическими основами квантовой механики.[72]
В 1925 г. после новаторской работы с Хендрик КрамерсГейзенберг разработал матричная механика, который заменил специальный старая квантовая теория с современной квантовой механикой. Центральная посылка заключалась в том, что классическая концепция движения не подходит на квантовом уровне, поскольку электроны в атоме не движутся по четко определенным орбитам. Скорее движение их странным образом смазано: преобразование Фурье его временной зависимости включают только те частоты, которые можно было бы наблюдать в квантовых скачках их излучения.
Статья Гейзенберга не допускала каких-либо ненаблюдаемых величин, таких как точное положение электрона на орбите в любое время; он позволил теоретику говорить только о фурье-компонентах движения. Поскольку компоненты Фурье не были определены на классических частотах, их нельзя было использовать для построения точного траектория, так что формализм не мог ответить на некоторые излишне точные вопросы о том, где находится электрон и как быстро он движется.
В марте 1926 года, работая в институте Бора, Гейзенберг понял, что не-коммутативность подразумевает принцип неопределенности. Этот вывод обеспечил четкую физическую интерпретацию некоммутативности и заложил основу для того, что стало известно как Копенгагенская интерпретация квантовой механики. Гейзенберг показал, что соотношение коммутации подразумевает неопределенность, или, говоря языком Бора, взаимодополняемость.[73] Любые две переменные, которые не коммутируют, нельзя измерить одновременно - чем точнее известна одна, тем менее точно может быть известна другая. Гейзенберг писал:
В простейшей форме это можно выразить следующим образом: невозможно узнать с полной точностью оба этих двух важных фактора, которые определяют движение одной из мельчайших частиц, - ее положение и скорость. Невозможно точно определить обе положение, направление и скорость частицы в то же время.[74]
В своей знаменитой статье 1927 года «Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik» («О воспринимаемом содержании квантовой теоретической кинематики и механики») Гейзенберг установил это выражение как минимальную величину неизбежного возмущения импульса, вызываемого любым измерением положения[2] но он не дал точного определения неопределенностей Δx и Δp. Вместо этого он дал правдоподобные оценки для каждого случая отдельно. В своей чикагской лекции[75] он уточнил свой принцип:
(1)
Кеннард[3] в 1927 году впервые доказал современное неравенство:
(2)
куда час = час/2π, и σИкс, σп стандартные отклонения положения и импульса. Гейзенберг только доказал соотношение (2) для частного случая гауссовских состояний.[75]
Терминология и перевод
В основной части своей оригинальной статьи 1927 года, написанной на немецком языке, Гейзенберг использовал слово «Ungenauigkeit» («неопределенность»),[2]описать основной теоретический принцип. Только в примечании он перешел на слово «Unsicherheit» («неопределенность»). Когда англоязычная версия учебника Гейзенберга, Физические принципы квантовой теории, был опубликован в 1930 году, однако использовался перевод «неопределенность», и с тех пор он стал более часто используемым термином в английском языке.[76]
Микроскоп Гейзенберга

Этот принцип довольно противоречит интуиции, поэтому первых студентов, изучающих квантовую теорию, нужно было заверить, что наивные измерения, нарушающие его, всегда были неработоспособны. Один из способов, которым Гейзенберг первоначально продемонстрировал внутреннюю невозможность нарушения принципа неопределенности, - это использование эффект наблюдателя воображаемого микроскопа как измерительного прибора.[75]
Он представляет себе экспериментатора, пытающегося измерить положение и импульс электрон стреляя в фотон на него.[77]:49–50
- Проблема 1. Если у фотона короткое замыкание длина волны, а значит, большой импульс позволяет точно измерить положение. Но фотон рассеивается в случайном направлении, передавая электрону большой и неопределенный импульс. Если у фотона длинный длина волны и малом импульсе столкновение не сильно нарушает импульс электрона, но рассеяние лишь смутно покажет его положение.
- Проблема 2 - Если большой отверстие используется для микроскопа, местоположение электрона может быть хорошо разрешено (см. Критерий Рэлея); но по принципу сохранение импульсапоперечный импульс входящего фотона влияет на импульс электронного пучка, и, следовательно, новый импульс электрона плохо разрешается. Если используется малая диафрагма, точность обоих разрешений будет наоборот.
Комбинация этих компромиссов означает, что независимо от того, какая длина волны фотона и размер апертуры используются, произведение неопределенности измеренного положения и измеренного импульса больше или равно нижнему пределу, который составляет (с точностью до небольшого числового коэффициента ) равно Постоянная Планка.[78] Гейзенберг не позаботился сформулировать принцип неопределенности как точный предел и предпочел использовать его вместо этого как эвристическое количественное утверждение, исправляющее с точностью до небольших числовых факторов, что делает неизбежной радикально новую некоммутативность квантовой механики.
Критические реакции
Копенгагенская интерпретация квантовой механики и принцип неопределенности Гейзенберга фактически рассматривались недоброжелателями как двойная цель. детерминизм и реализм. Согласно Копенгагенская интерпретация квантовой механики не существует фундаментальной реальности, что квантовое состояние описывает, просто рецепт для расчета экспериментальных результатов. Невозможно сказать, каково фундаментальное состояние системы, только каковы могут быть результаты наблюдений.
Альберт Эйнштейн считал, что случайность - это отражение нашего незнания некоторых фундаментальных свойств реальности, в то время как Нильс Бор считал, что распределения вероятностей фундаментальны и неприводимы, и зависят от того, какие измерения мы выбираем для выполнения. Эйнштейн и Бор спорили принцип неопределенности на многие годы.
Идеал стороннего наблюдателя
Вольфганг Паули назвал фундаментальное возражение Эйнштейна против принципа неопределенности «идеалом стороннего наблюдателя» (фраза в переводе с немецкого):
«Подобно тому, как Луна имеет определенное положение, - сказал мне Эйнштейн прошлой зимой, - независимо от того, смотрим ли мы на Луну или нет, то же самое должно иметь место и для атомных объектов, поскольку между ними и макроскопическими объектами нет четкого различия. Наблюдение не можешь Создайте элемент реальности, такой как позиция, в полном описании физической реальности должно содержаться что-то, что соответствует возможность наблюдения позиции, еще до того, как наблюдение было фактически сделано. "Я надеюсь, что я правильно процитировал Эйнштейна; всегда трудно цитировать кого-то по памяти, с кем не согласен. Именно такой постулат я называют идеалом стороннего наблюдателя.
- Письмо Паули Нильсу Бору, 15 февраля 1955 г.[79]
Щель Эйнштейна
The first of Einstein's мысленные эксперименты challenging the uncertainty principle went as follows:
- Consider a particle passing through a slit of width d. The slit introduces an uncertainty in momentum of approximately час/d because the particle passes through the wall. But let us determine the momentum of the particle by measuring the recoil of the wall. In doing so, we find the momentum of the particle to arbitrary accuracy by conservation of momentum.
Bohr's response was that the wall is quantum mechanical as well, and that to measure the recoil to accuracy Δп, the momentum of the wall must be known to this accuracy before the particle passes through. This introduces an uncertainty in the position of the wall and therefore the position of the slit equal to час/Δп, and if the wall's momentum is known precisely enough to measure the recoil, the slit's position is uncertain enough to disallow a position measurement.
A similar analysis with particles diffracting through multiple slits is given by Ричард Фейнман.[80]
Ящик Эйнштейна
Bohr was present when Einstein proposed the thought experiment which has become known as Ящик Эйнштейна. Einstein argued that "Heisenberg's uncertainty equation implied that the uncertainty in time was related to the uncertainty in energy, the product of the two being related to Постоянная Планка."[81] Consider, he said, an ideal box, lined with mirrors so that it can contain light indefinitely. The box could be weighed before a clockwork mechanism opened an ideal shutter at a chosen instant to allow one single photon to escape. "We now know, explained Einstein, precisely the time at which the photon left the box."[82] "Now, weigh the box again. The change of mass tells the energy of the emitted light. In this manner, said Einstein, one could measure the energy emitted and the time it was released with any desired precision, in contradiction to the uncertainty principle."[81]
Bohr spent a sleepless night considering this argument, and eventually realized that it was flawed. He pointed out that if the box were to be weighed, say by a spring and a pointer on a scale, "since the box must move vertically with a change in its weight, there will be uncertainty in its vertical velocity and therefore an uncertainty in its height above the table. ... Furthermore, the uncertainty about the elevation above the earth's surface will result in an uncertainty in the rate of the clock,"[83] because of Einstein's own theory of gravity's effect on time."Through this chain of uncertainties, Bohr showed that Einstein's light box experiment could not simultaneously measure exactly both the energy of the photon and the time of its escape."[84]
Парадокс ЭПР для запутанных частиц
Bohr was compelled to modify his understanding of the uncertainty principle after another thought experiment by Einstein. In 1935, Einstein, Podolsky and Rosen (see Парадокс ЭПР) published an analysis of widely separated запутанный частицы. Measuring one particle, Einstein realized, would alter the probability distribution of the other, yet here the other particle could not possibly be disturbed. This example led Bohr to revise his understanding of the principle, concluding that the uncertainty was not caused by a direct interaction.[85]
But Einstein came to much more far-reaching conclusions from the same thought experiment. He believed the "natural basic assumption" that a complete description of reality would have to predict the results of experiments from "locally changing deterministic quantities" and therefore would have to include more information than the maximum possible allowed by the uncertainty principle.
В 1964 г. Джон Белл showed that this assumption can be falsified, since it would imply a certain inequality between the probabilities of different experiments. Experimental results confirm the predictions of quantum mechanics, ruling out Einstein's basic assumption that led him to the suggestion of his скрытые переменные. These hidden variables may be "hidden" because of an illusion that occurs during observations of objects that are too large or too small. This illusion can be likened to rotating fan blades that seem to pop in and out of existence at different locations and sometimes seem to be in the same place at the same time when observed. This same illusion manifests itself in the observation of subatomic particles. Both the fan blades and the subatomic particles are moving so fast that the illusion is seen by the observer. Therefore, it is possible that there would be predictability of the subatomic particles behavior and characteristics to a recording device capable of very high speed tracking....Ironically this fact is one of the best pieces of evidence supporting Карл Попперфилософия invalidation of a theory by falsification-experiments. That is to say, here Einstein's "basic assumption" became falsified by experiments based on Bell's inequalities. For the objections of Karl Popper to the Heisenberg inequality itself, see below.
While it is possible to assume that quantum mechanical predictions are due to nonlocal, hidden variables, and in fact Дэвид Бом invented such a formulation, this resolution is not satisfactory to the vast majority of physicists. The question of whether a random outcome is predetermined by a nonlocal theory can be philosophical, and it can be potentially intractable. If the hidden variables were not constrained, they could just be a list of random digits that are used to produce the measurement outcomes. To make it sensible, the assumption of nonlocal hidden variables is sometimes augmented by a second assumption—that the размер наблюдаемой Вселенной puts a limit on the computations that these variables can do. A nonlocal theory of this sort predicts that a квантовый компьютер would encounter fundamental obstacles when attempting to factor numbers of approximately 10,000 digits or more; a potentially achievable task in quantum mechanics.[86][требуется полная цитата]
Критика Поппера
Карл Поппер approached the problem of indeterminacy as a logician and metaphysical realist.[87] He disagreed with the application of the uncertainty relations to individual particles rather than to ансамбли of identically prepared particles, referring to them as "statistical scatter relations".[87][88] In this statistical interpretation, a частности measurement may be made to arbitrary precision without invalidating the quantum theory. This directly contrasts with the Копенгагенская интерпретация of quantum mechanics, which is недетерминированный but lacks local hidden variables.
In 1934, Popper published Zur Kritik der Ungenauigkeitsrelationen (Critique of the Uncertainty Relations) в Naturwissenschaften,[89] и в том же году Logik der Forschung (translated and updated by the author as Логика научных открытий in 1959), outlining his arguments for the statistical interpretation. In 1982, he further developed his theory in Quantum theory and the schism in Physics, письмо:
[Heisenberg's] formulae are, beyond all doubt, derivable statistical formulae of the quantum theory. But they have been habitually misinterpreted by those quantum theorists who said that these formulae can be interpreted as determining some upper limit to the precision of our measurements. [original emphasis][90]
Popper proposed an experiment to фальсифицировать the uncertainty relations, although he later withdrew his initial version after discussions with Weizsäcker, Гейзенберг, и Эйнштейн; this experiment may have influenced the formulation of the EPR experiment.[87][91]
Многомировая неопределенность
В многомировая интерпретация originally outlined by Хью Эверетт III in 1957 is partly meant to reconcile the differences between Einstein's and Bohr's views by replacing Bohr's коллапс волновой функции with an ensemble of deterministic and independent universes whose распределение is governed by волновые функции и Уравнение Шредингера. Thus, uncertainty in the many-worlds interpretation follows from each observer within any universe having no knowledge of what goes on in the other universes.
Свободная воля
Some scientists including Артур Комптон[92] и Martin Heisenberg[93] have suggested that the uncertainty principle, or at least the general probabilistic nature of quantum mechanics, could be evidence for the two-stage model of free will. One critique, however, is that apart from the basic role of quantum mechanics as a foundation for chemistry, nontrivial biological mechanisms requiring quantum mechanics are unlikely, due to the rapid декогеренция time of quantum systems at room temperature.[94] Proponents of this theory commonly say that this decoherence is overcome by both screening and decoherence-free subspaces found in biological cells.[94]
Термодинамика
There is reason to believe that violating the uncertainty principle also strongly implies the violation of the второй закон термодинамики.[95] Видеть Gibbs paradox.
Смотрите также
- Афшар эксперимент
- Каноническое коммутационное отношение
- Принцип соответствия
- Correspondence rules
- Gromov's non-squeezing theorem
- Discrete Fourier transform#Uncertainty principle
- Einstein's thought experiments
- Heisenbug
- Введение в квантовую механику
- Операционализация
- Эффект наблюдателя (информационные технологии)
- Эффект наблюдателя (физика)
- Quantum indeterminacy
- Quantum non-equilibrium
- Квантовое туннелирование
- Физика и не только (книга)
- Планковская длина
- Более сильные отношения неопределенности
- Weak measurement
Примечания
- ^ N.B. на точность: Если и are the precisions of position and momentum obtained in an индивидуальный измерение и , their standard deviations in an ансамбль of individual measurements on similarly prepared systems, then "There are, in principle, no restrictions on the precisions of individual measurements и , but the standard deviations will always satisfy ".[11]
- ^ Note 1 is in clear contradiction with the Section Систематические и статистические ошибки that states the existence of both statistical (Robertson) and systematic (Heisenberg) uncertainty relations. These uncertainties are simultaneously expressed in Ozawa's or in Fujikawa's universal inequalities.
Рекомендации
- ^ а б c Sen, D. (2014). "The Uncertainty relations in quantum mechanics" (PDF). Текущая наука. 107 (2): 203–218.
- ^ а б c Heisenberg, W. (1927), "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik", Zeitschrift für Physik (на немецком), 43 (3–4): 172–198, Bibcode:1927ZPhy ... 43..172H, Дои:10.1007 / BF01397280, S2CID 122763326..Annotated pre-publication proof sheet of Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik, 21 марта 1927 г.
- ^ а б c Kennard, E. H. (1927), "Zur Quantenmechanik einfacher Bewegungstypen", Zeitschrift für Physik (на немецком), 44 (4–5): 326–352, Bibcode:1927ZPhy...44..326K, Дои:10.1007/BF01391200, S2CID 121626384.
- ^ Weyl, H. (1928), Gruppentheorie und Quantenmechanik, Leipzig: Hirzel
- ^ Furuta, Aya (2012), "One Thing Is Certain: Heisenberg's Uncertainty Principle Is Not Dead", Scientific American
- ^ а б Ozawa, Masanao (2003), "Universally valid reformulation of the Heisenberg uncertainty principle on noise and disturbance in measurement", Физический обзор A, 67 (4): 42105, arXiv:quant-ph/0207121, Bibcode:2003PhRvA..67d2105O, Дои:10.1103/PhysRevA.67.042105, S2CID 42012188
- ^ Вернер Гейзенберг, Физические принципы квантовой теории, п. 20
- ^ а б Rozema, L. A.; Darabi, A.; Mahler, D. H.; Hayat, A.; Soudagar, Y.; Steinberg, A. M. (2012). "Violation of Heisenberg's Measurement–Disturbance Relationship by Weak Measurements". Письма с физическими проверками. 109 (10): 100404. arXiv:1208.0034v2. Bibcode:2012PhRvL.109j0404R. Дои:10.1103/PhysRevLett.109.100404. PMID 23005268. S2CID 37576344.
- ^ Indian Institute of Technology Madras, Professor V. Balakrishnan, Lecture 1 – Introduction to Quantum Physics; Heisenberg's uncertainty principle, National Programme of Technology Enhanced Learning на YouTube
- ^ а б c d Л.Д. Ландо, E. M. Lifshitz (1977). Quantum Mechanics: Non-Relativistic Theory. Vol. 3 (3rd ed.). Pergamon Press. ISBN 978-0-08-020940-1. Интернет-копия.
- ^ Section 3.2 of Ballentine, Leslie E. (1970), "The Statistical Interpretation of Quantum Mechanics", Обзоры современной физики, 42 (4): 358–381, Bibcode:1970РвМП ... 42..358Б, Дои:10.1103/RevModPhys.42.358. This fact is experimentally well-known for example in quantum optics (see e.g. chap. 2 and Fig. 2.1 Leonhardt, Ulf (1997), Measuring the Quantum State of Light, Кембридж: Издательство Кембриджского университета, ISBN 0-521-49730-2
- ^ Elion, W. J.; M. Matters, U. Geigenmüller & J. E. Mooij; Geigenmüller, U.; Mooij, J. E. (1994), "Direct demonstration of Heisenberg's uncertainty principle in a superconductor", Природа, 371 (6498): 594–595, Bibcode:1994Natur.371..594E, Дои:10.1038y/371594a0 (inactive 2020-09-12)CS1 maint: DOI неактивен по состоянию на сентябрь 2020 г. (связь)
- ^ Smithey, D. T.; M. Beck, J. Cooper, M. G. Raymer; Cooper, J.; Raymer, M. G. (1993), "Measurement of number–phase uncertainty relations of optical fields", Phys. Ред. А, 48 (4): 3159–3167, Bibcode:1993PhRvA..48.3159S, Дои:10.1103/PhysRevA.48.3159, PMID 9909968CS1 maint: несколько имен: список авторов (связь)
- ^ Caves, Carlton (1981), "Quantum-mechanical noise in an interferometer", Phys. Ред. D, 23 (8): 1693–1708, Bibcode:1981ПхРвД..23.1693С, Дои:10.1103/PhysRevD.23.1693
- ^ Jaeger, Gregg (September 2014). "What in the (quantum) world is macroscopic?". Американский журнал физики. 82 (9): 896–905. Bibcode:2014AmJPh..82..896J. Дои:10.1119/1.4878358.
- ^ Claude Cohen-Tannoudji; Bernard Diu; Franck Laloë (1996), Квантовая механика, Wiley-Interscience: Wiley, pp. 231–233, ISBN 978-0-471-56952-7
- ^ Giovannetti, V.; Lloyd, S .; Maccone, L. (2011). "Advances in quantum metrology". Природа Фотоника. 5 (4): 222. arXiv:1102.2318. Bibcode:2011NaPho...5..222G. Дои:10.1038/nphoton.2011.35. S2CID 12591819.; arXiv
- ^ Luis, Alfredo (2017-03-13). "Breaking the weak Heisenberg limit". Физический обзор A. 95 (3): 032113. arXiv:1607.07668. Bibcode:2017PhRvA..95c2113L. Дои:10.1103/PhysRevA.95.032113. ISSN 2469-9926. S2CID 55838380.
- ^ а б Robertson, H. P. (1929), "The Uncertainty Principle", Phys. Ред., 34 (1): 163–64, Bibcode:1929ПхРв ... 34..163Р, Дои:10.1103 / PhysRev.34.163
- ^ а б Schrödinger, E. (1930), "Zum Heisenbergschen Unschärfeprinzip", Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse, 14: 296–303
- ^ а б Griffiths, David (2005), Квантовая механика, New Jersey: Pearson
- ^ Riley, K. F.; M. P. Hobson and S. J. Bence (2006), Математические методы для физики и инженерии, Кембридж, стр. 246
- ^ Davidson, E. R. (1965), "On Derivations of the Uncertainty Principle", J. Chem. Phys., 42 (4): 1461–1462, Bibcode:1965JChPh..42.1461D, Дои:10.1063/1.1696139
- ^ а б c Холл, Б. С. (2013), Квантовая теория для математиков, Springer, стр. 245
- ^ а б Jackiw, Roman (1968), "Minimum Uncertainty Product, Number‐Phase Uncertainty Product, and Coherent States", J. Math. Phys., 9 (3): 339–346, Bibcode:1968JMP.....9..339J, Дои:10.1063/1.1664585
- ^ а б Carruthers, P.; Nieto, M. M. (1968), "Phase and Angle Variables in Quantum Mechanics", Ред. Мод. Phys., 40 (2): 411–440, Bibcode:1968RvMP...40..411C, Дои:10.1103/RevModPhys.40.411
- ^ Холл, Б. С. (2013), Квантовая теория для математиков, Springer
- ^ Макконе, Лоренцо; Пати, Арун К. (31 декабря 2014 г.). «Более сильные отношения неопределенности для всех несовместимых наблюдаемых». Письма с физическими проверками. 113 (26): 260401. arXiv:1407.0338. Bibcode:2014PhRvL.113z0401M. Дои:10.1103/PhysRevLett.113.260401. PMID 25615288.
- ^ Хуан, Ичэнь (10 августа 2012 г.). «Отношения неопределенности на основе дисперсии». Физический обзор A. 86 (2): 024101. arXiv:1012.3105. Bibcode:2012PhRvA..86b4101H. Дои:10.1103 / PhysRevA.86.024101. S2CID 118507388.
- ^ Curtright, T .; Zachos, C. (2001). "Negative Probability and Uncertainty Relations". Буквы A по современной физике. 16 (37): 2381–2385. arXiv:hep-th/0105226. Bibcode:2001MPLA...16.2381C. Дои:10.1142/S021773230100576X. S2CID 119669313.
- ^ L. I. Mandelshtam, I. E. Tamm, The uncertainty relation between energy and time in nonrelativistic quantum mechanics, 1945.
- ^ Hilgevoord, Jan (1996). "The uncertainty principle for energy and time" (PDF). Американский журнал физики. 64 (12): 1451–1456. Bibcode:1996AmJPh..64.1451H. Дои:10.1119/1.18410.; Hilgevoord, Jan (1998). "The uncertainty principle for energy and time. II". Американский журнал физики. 66 (5): 396–402. Bibcode:1998AmJPh..66..396H. Дои:10.1119/1.18880.; Busch, P. (1990). "On the energy-time uncertainty relation. Part I: Dynamical time and time indeterminacy", Основы физики 20(1), 1-32; Busch, P. (1990), "On the energy-time uncertainty relation. Part II: Pragmatic time versus energy indeterminacy". Основы физики 20(1), 33-43.
- ^ The broad linewidth of fast-decaying states makes it difficult to accurately measure the energy of the state, and researchers have even used detuned microwave cavities to slow down the decay rate, to get sharper peaks. Габриэль, Джеральд; H. Dehmelt (1985), "Observation of Inhibited Spontaneous Emission", Письма с физическими проверками, 55 (1): 67–70, Bibcode:1985PhRvL..55...67G, Дои:10.1103/PhysRevLett.55.67, PMID 10031682
- ^ Likharev, K. K.; A. B. Zorin (1985), "Theory of Bloch-Wave Oscillations in Small Josephson Junctions", J. Low Temp. Phys., 59 (3/4): 347–382, Bibcode:1985JLTP...59..347L, Дои:10.1007/BF00683782, S2CID 120813342
- ^ Anderson, P. W. (1964), "Special Effects in Superconductivity", in Caianiello, E. R. (ed.), Lectures on the Many-Body Problem, Vol. 2, Нью-Йорк: Academic Press
- ^ More precisely, whenever both и are defined, and the space of such is a dense subspace of the quantum Hilbert space. Видеть Холл, Б. С. (2013), Квантовая теория для математиков, Springer, стр. 245
- ^ Холл, Б. С. (2013), Квантовая теория для математиков, Springer, стр. 285
- ^ Холл, Б. С. (2013), Квантовая теория для математиков, Springer, стр. 246
- ^ Busch, P.; Lahti, P.; Werner, R. F. (2013). "Proof of Heisenberg's Error-Disturbance Relation". Письма с физическими проверками. 111 (16): 160405. arXiv:1306.1565. Bibcode:2013PhRvL.111p0405B. Дои:10.1103/PhysRevLett.111.160405. PMID 24182239. S2CID 24507489.
- ^ Busch, P.; Lahti, P.; Werner, R. F. (2014). "Heisenberg uncertainty for qubit measurements". Физический обзор A. 89 (1): 012129. arXiv:1311.0837. Bibcode:2014PhRvA..89a2129B. Дои:10.1103/PhysRevA.89.012129. S2CID 118383022.
- ^ Erhart, J.; Sponar, S.; Sulyok, G.; Badurek, G.; Ozawa, M.; Hasegawa, Y. (2012). "Experimental demonstration of a universally valid error-disturbance uncertainty relation in spin measurements". Природа Физика. 8 (3): 185–189. arXiv:1201.1833. Bibcode:2012NatPh...8..185E. Дои:10.1038/nphys2194. S2CID 117270618.
- ^ Baek, S.-Y.; Kaneda, F.; Ozawa, M.; Edamatsu, K. (2013). "Experimental violation and reformulation of the Heisenberg's error-disturbance uncertainty relation". Научные отчеты. 3: 2221. Bibcode:2013NatSR...3E2221B. Дои:10.1038/srep02221. ЧВК 3713528. PMID 23860715.
- ^ Ringbauer, M.; Biggerstaff, D.N.; Broome, M.A.; Fedrizzi, A.; Branciard, C .; White, A.G. (2014). "Experimental Joint Quantum Measurements with Minimum Uncertainty". Письма с физическими проверками. 112 (2): 020401. arXiv:1308.5688. Bibcode:2014PhRvL.112b0401R. Дои:10.1103/PhysRevLett.112.020401. PMID 24483993. S2CID 18730255.
- ^ Björk, G.; Söderholm, J.; Trifonov, A.; Tsegaye, T.; Karlsson, A. (1999). "Complementarity and the uncertainty relations". Физический обзор. A60 (3): 1878. arXiv:quant-ph/9904069. Bibcode:1999PhRvA..60.1874B. Дои:10.1103/PhysRevA.60.1874. S2CID 27371899.
- ^ Fujikawa, Kazuo (2012). "Universally valid Heisenberg uncertainty relation". Физический обзор A. 85 (6): 062117. arXiv:1205.1360. Bibcode:2012PhRvA..85f2117F. Дои:10.1103/PhysRevA.85.062117. S2CID 119640759.
- ^ Judge, D. (1964), "On the uncertainty relation for angle variables", Il Nuovo Cimento, 31 (2): 332–340, Bibcode:1964NCim...31..332J, Дои:10.1007/BF02733639, S2CID 120553526
- ^ Bouten, M.; Maene, N.; Van Leuven, P. (1965), "On an uncertainty relation for angle variables", Il Nuovo Cimento, 37 (3): 1119–1125, Bibcode:1965NCim...37.1119B, Дои:10.1007/BF02773197, S2CID 122838645
- ^ Louisell, W. H. (1963), "Amplitude and phase uncertainty relations", Письма по физике, 7 (1): 60–61, Bibcode:1963PhL.....7...60L, Дои:10.1016/0031-9163(63)90442-6
- ^ DeWitt, B. S.; Graham, N. (1973), Многомировая интерпретация квантовой механики, Princeton: Princeton University Press, pp. 52–53, ISBN 0-691-08126-3
- ^ Hirschman, I. I., Jr. (1957), "A note on entropy", American Journal of Mathematics, 79 (1): 152–156, Дои:10.2307/2372390, JSTOR 2372390.
- ^ Beckner, W. (1975), "Inequalities in Fourier analysis", Анналы математики, 102 (6): 159–182, Дои:10.2307/1970980, JSTOR 1970980, ЧВК 432369, PMID 16592223.
- ^ Bialynicki-Birula, I.; Mycielski, J. (1975), "Uncertainty Relations for Information Entropy in Wave Mechanics", Коммуникации по математической физике, 44 (2): 129–132, Bibcode:1975CMaPh..44..129B, Дои:10.1007/BF01608825, S2CID 122277352
- ^ Huang, Yichen (24 May 2011). "Entropic uncertainty relations in multidimensional position and momentum spaces". Физический обзор A. 83 (5): 052124. arXiv:1101.2944. Bibcode:2011PhRvA..83e2124H. Дои:10.1103/PhysRevA.83.052124. S2CID 119243096.
- ^ Chafaï, D. (2003), «Гауссовский максимум энтропии и обратное логарифмическое неравенство Соболева», Séminaire de Probabilités XXXVI, Конспект лекций по математике, 1801, стр. 194–200, arXiv:математика / 0102227, Дои:10.1007/978-3-540-36107-7_5, ISBN 978-3-540-00072-3, S2CID 17795603
- ^ Ефимов, Сергей П. (1976). «Математическая формулировка отношений неопределенности». Российский физический журнал. 19 (3): 95–99. Bibcode:1976SvPhJ..19..340E. Дои:10.1007 / BF00945688. S2CID 121735555.
- ^ Додонов, В. (2019). «Отношения неопределенности для нескольких наблюдаемых через алгебры Клиффорда». Journal of Physics: Серия конференций. 1194 012028 (1): 012028. Bibcode:2019JPhCS1194a2028D. Дои:10.1088/1742-6596/1194/1/012028.
- ^ а б Додонов, В. В. (2018). «Дисперсионные отношения неопределенности без ковариаций для трех и четырех наблюдаемых». Физический обзор A. 37 (2): 022105. Дои:10.1103 / PhysRevA97.022105 (неактивно 12.09.2020).CS1 maint: DOI неактивен по состоянию на сентябрь 2020 г. (связь)
- ^ Havin, V .; Йерике, Б. (1994), Принцип неопределенности в гармоническом анализе, Springer-Verlag
- ^ Фолланд, Джеральд; Ситарам, Аллади (май 1997 г.), «Принцип неопределенности: математический обзор», Журнал анализа Фурье и приложений, 3 (3): 207–238, Дои:10.1007 / BF02649110, МИСТЕР 1448337, S2CID 121355943
- ^ Ситарам, А. (2001) [1994], «Принцип неопределенности, математический», Энциклопедия математики, EMS Press
- ^ Мэтт Холл, «Что такое принцип неопределенности Габора?»
- ^ Donoho, D.L .; Старк, П. Б. (1989). «Принципы неопределенности и восстановление сигнала». Журнал SIAM по прикладной математике. 49 (3): 906–931. Дои:10.1137/0149053.
- ^ Amrein, W.O .; Бертье, А. (1977), "О опорных свойствах Lп-функции и их преобразования Фурье », Журнал функционального анализа, 24 (3): 258–267, Дои:10.1016/0022-1236(77)90056-8.
- ^ Бенедикс, М. (1985), "О преобразованиях Фурье функций с носителями на множествах конечной меры Лебега", J. Math. Анальный. Appl., 106 (1): 180–183, Дои:10.1016 / 0022-247X (85) 90140-4
- ^ Назаров, Ф. (1994), "Локальные оценки экспоненциальных многочленов и их приложения к неравенствам типа принципа неопределенности", Санкт-Петербургская математика. Дж., 5: 663–717
- ^ Джейминг, доктор наук (2007), "Принципы неопределенности Назарова в более высоком измерении", J. Прибл. Теория, 149 (1): 30–41, arXiv:математика / 0612367, Дои:10.1016 / j.jat.2007.04.005, S2CID 9794547
- ^ Харди, Г. (1933), «Теорема о преобразованиях Фурье», Журнал Лондонского математического общества, 8 (3): 227–231, Дои:10.1112 / jlms / s1-8.3.227
- ^ Хёрмандер, Л. (1991), "Теорема единственности Берлинга для пар преобразований Фурье", Арк. Мат., 29 (1–2): 231–240, Bibcode:1991ArM .... 29..237H, Дои:10.1007 / BF02384339, S2CID 121375111
- ^ Бонами, А.; Деманж, Б .; Джейминг, доктор наук (2003), "Функции Эрмита и принципы неопределенности для Фурье и оконных преобразований Фурье", Преподобный Мат. Ибероамерикана, 19: 23–55, arXiv:математика / 0102111, Bibcode:2001математика ...... 2111B, Дои:10.4171 / RMI / 337, S2CID 1211391
- ^ Хеденмальм, Х. (2012), «Принцип неопределенности Гейзенберга в смысле Берлинга», J. Anal. Математика., 118 (2): 691–702, arXiv:1203.5222, Bibcode:2012arXiv1203.5222H, Дои:10.1007 / s11854-012-0048-9, S2CID 54533890
- ^ Деманж, Бруно (2009), Принципы неопределенности, связанные с невырожденными квадратичными формами, Société Mathématique de France, ISBN 978-2-85629-297-6
- ^ "Гейзенберг / Интернет-выставка неопределенности". Американский институт физики, Центр истории физики. Получено 2019-10-16.
- ^ Бор, Нильс; Нолл, Вальдемар (1958), "Атомная физика и человеческие знания", Американский журнал физики, Нью-Йорк: Wiley, 26 (8): 38, Bibcode:1958AmJPh..26..596B, Дои:10.1119/1.1934707
- ^ Гейзенберг, В., Die Physik der Atomkerne, Тейлор и Фрэнсис, 1952, стр. 30.
- ^ а б c Гейзенберг, В. (1930), Physikalische Prinzipien der Quantentheorie (на немецком языке), Лейпциг: Hirzel английский перевод Физические принципы квантовой теории. Чикаго: Издательство Чикагского университета, 1930.
- ^ Кэссиди, Дэвид; Саперштейн, Элвин М. (2009), «За пределами неопределенности: Гейзенберг, квантовая физика и бомба», Физика сегодня, Нью-Йорк: Bellevue Literary Press, 63 (1): 185, Bibcode:2010ФТ .... 63а..49С, Дои:10.1063/1.3293416
- ^ Джордж Гринштейн; Артур Зайонц (2006). Квантовая задача: современные исследования основ квантовой механики. Джонс и Бартлетт Обучение. ISBN 978-0-7637-2470-2.
- ^ Типлер, Пол А .; Ллевеллин, Ральф А. (1999), «5–5», Современная физика (3-е изд.), W.H. Freeman and Co., ISBN 1-57259-164-1
- ^ Enz, Charles P .; Мейенн, Карл фон, ред. (1994). Труды Вольфганга Паули по физике и философии. Springer-Verlag. п. 43. ISBN 3-540-56859-X; перевод Роберта Шлаппа
- ^ Лекции Фейнмана по физике, т. 3, 2–2
- ^ а б Гамов, Г., Великие физики от Галилея до Эйнштейна, Courier Dover, 1988, с.260.
- ^ Кумар, М., Квантовая: Эйнштейн, Бор и великие дебаты о природе реальности, Икона, 2009, с. 282.
- ^ Гамов, Г., Великие физики от Галилея до Эйнштейна, Courier Dover, 1988, с. 260–261.
- ^ Кумар, М., Квантовая: Эйнштейн, Бор и великие дебаты о природе реальности, Икона, 2009, с. 287.
- ^ Исааксон, Уолтер (2007), Эйнштейн: его жизнь и Вселенная, Нью-Йорк: Саймон и Шустер, стр.452, ISBN 978-0-7432-6473-0
- ^ Герардус т Хофт иногда отстаивал эту точку зрения.
- ^ а б c Поппер, Карл (1959), Логика научных открытий, Hutchinson & Co.
- ^ Джарви, Ян Чарльз; Милфорд, Карл; Миллер, Дэвид В. (2006), Карл Поппер: оценка столетия, 3, Издательство Ashgate, ISBN 978-0-7546-5712-5
- ^ Поппер, Карл; Карл Фридрих фон Вайцзеккер (1934), «Zur Kritik der Ungenauigkeitsrelationen (Критика отношений неопределенности)», Naturwissenschaften, 22 (48): 807–808, Bibcode:1934NW ..... 22..807P, Дои:10.1007 / BF01496543, S2CID 40843068.
- ^ Поппер, К. Квантовая теория и раскол в физике, Unwin Hyman Ltd, 1982, стр. 53–54.
- ^ Мехра, Джагдиш; Рехенберг, Гельмут (2001), Историческое развитие квантовой теории, Спрингер, ISBN 978-0-387-95086-0
- ^ Комптон, А. Х. (1931). «Принцип неопределенности и свободы воли». Наука. 74 (1911): 172. Bibcode:1931Научный .... 74..172С. Дои:10.1126 / science.74.1911.172. PMID 17808216.
- ^ Гейзенберг, М. (2009). «Неужели свобода воли - иллюзия?». Природа. 459 (7244): 164–165. Bibcode:2009Натура.459..164H. Дои:10.1038 / 459164a. PMID 19444190. S2CID 4420023.
- ^ а б Дэвис, П. К. У. (2004). «Квантовая механика играет нетривиальную роль в жизни?». Биосистемы. 78 (1–3): 69–79. Дои:10.1016 / j.biosystems.2004.07.001. PMID 15555759.
- ^ Хангги, Эстер; Венер, Стефани (2013). «Нарушение принципа неопределенности означает нарушение второго закона термодинамики». Nature Communications. 4: 1670. arXiv:1205.6894. Bibcode:2013 НатКо ... 4.1670H. Дои:10.1038 / ncomms2665. PMID 23575674. S2CID 205316392.
внешняя ссылка
| В Wikiquote есть цитаты, связанные с: Принцип неопределенности |
- «Принцип неопределенности», Энциклопедия математики, EMS Press, 2001 [1994]
- Материя как волна - глава из онлайн-учебника
- Квантовая механика: мифы и факты
- Стэнфордская энциклопедия философии
- Преобразования Фурье и неопределенность на MathPages
- aip.org: Квантовая механика 1925–1927 - Принцип неопределенности
- Мир физики Эрика Вайсштейна - принцип неопределенности
- Джон Баэз о соотношении неопределенности времени и энергии
- Принцип достоверности
- Распространенное толкование принципа неопределенности Гейзенберга оказалось ложным






![operatorname {P} [a leq X leq b] = int _ {a} ^ {b} | psi (x) | ^ {2} , mathrm {d} x ~.](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8852ff1f2e7c518fce8dfbb77f8e8a7920c63f3)













![{ displaystyle { begin {align} g (x) & = { frac {1} { sqrt {2 pi hbar}}} cdot int _ {- infty} ^ { infty} { тильда {g}} (p) cdot e ^ {ipx / hbar} , dp & = { frac {1} { sqrt {2 pi hbar}}} int _ {- infty } ^ { infty} p cdot varphi (p) cdot e ^ {ipx / hbar} , dp & = { frac {1} {2 pi hbar}} int _ {- infty} ^ { infty} left [p cdot int _ {- infty} ^ { infty} psi ( chi) e ^ {- ip chi / hbar} , d chi right] cdot e ^ {ipx / hbar} , dp & = { frac {i} {2 pi}} int _ {- infty} ^ { infty} left [{ cancel { left. psi ( chi) e ^ {- ip chi / hbar} right | _ {- infty} ^ { infty}}} - int _ {- infty} ^ { infty } { frac {d psi ( chi)} {d chi}} e ^ {- ip chi / hbar} , d chi right] cdot e ^ {ipx / hbar} , dp & = { frac {-i} {2 pi}} int _ {- infty} ^ { infty} int _ {- infty} ^ { infty} { frac {d psi ( chi)} {d chi}} e ^ {- ip chi / hbar} , d chi , e ^ {ipx / hbar} , dp & = left (-i hbar { frac {d} {dx}} right) cdot psi (x), end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42db5a07d8c895b1e9caffa2cde0b6df608ec8f8)







![{ displaystyle { begin {align} langle f mid g rangle - langle g mid f rangle = {} & int _ {- infty} ^ { infty} psi ^ {*} ( x) , x cdot left (-i hbar { frac {d} {dx}} right) , psi (x) , dx & {} - int _ {- infty } ^ { infty} psi ^ {*} (x) , left (-i hbar { frac {d} {dx}} right) cdot x , psi (x) , dx = {} & i hbar cdot int _ {- infty} ^ { infty} psi ^ {*} (x) left [ left (-x cdot { frac {d psi ( x)} {dx}} right) + { frac {d (x psi (x))} {dx}} right] , dx = {} & i hbar cdot int _ {- infty} ^ { infty} psi ^ {*} (x) left [ left (-x cdot { frac {d psi (x)} {dx}} right) + psi (x ) + left (x cdot { frac {d psi (x)} {dx}} right) right] , dx = {} & i hbar cdot int _ {- infty} ^ { infty} psi ^ {*} (x) psi (x) , dx = {} & i hbar cdot int _ {- infty} ^ { infty} | psi (x ) | ^ {2} , dx = {} & i hbar end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4ddead3f7e2d237c2ad9bb5258ad66a9d92c599)


![[{ hat {A}}, { hat {B}}] = { hat {A}} { hat {B}} - { hat {B}} { hat {A}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/3133da214f8f0fcf1ba11e907cfd121a2179b1b4)
![[{ hat {x}}, { hat {p}}] = i hbar.](https://wikimedia.org/api/rest_v1/media/math/render/svg/fee0861ae7784cb51a1b43f6c51735c22c23274e)


![{ displaystyle [{ hat {x}}, { hat {p}}] | psi rangle = ({ hat {x}} { hat {p}} - { hat {p}} { hat {x}}) | psi rangle = ({ hat {x}} - x_ {0} { hat {I}}) { hat {p}} , | psi rangle = i hbar | psi rangle,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8255257353e4743e966c106dea5674689ed04690)

![[{ hat {x}}, { hat {p}}] | psi rangle = i hbar | psi rangle neq 0.](https://wikimedia.org/api/rest_v1/media/math/render/svg/04d341bbd1c29d8f96a5ce5ad6e2cf856d1b1f40)







![[ hat {A}, hat {B}] = hat {A} hat {B} - hat {B} hat {A},](https://wikimedia.org/api/rest_v1/media/math/render/svg/9814a77ea436e956fd7abaad7b5906457037b565)
![{ displaystyle sigma _ {A} sigma _ {B} geq left | { frac {1} {2i}} langle [{ hat {A}}, { hat {B}}] rangle right | = { frac {1} {2}} left | langle [{ hat {A}}, { hat {B}}] rangle right |,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e237cc47d6a6ffaf614f696672356c362f84ac0)
![{ displaystyle sigma _ {A} ^ {2} sigma _ {B} ^ {2} geq left | { frac {1} {2}} langle {{ hat {A}}, { hat {B}} } rangle - langle { hat {A}} rangle langle { hat {B}} rangle right | ^ {2} + left | { frac {1 } {2i}} langle [{ hat {A}}, { hat {B}}] rangle right | ^ {2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81d7a893fe43757553fb6a3e5a51cdb83290aadd)



















![{ displaystyle { begin {align} langle f mid g rangle & = langle Psi | ({ hat {A}} - langle { hat {A}} rangle) ({ hat { B}} - langle { hat {B}} rangle) Psi rangle [4pt] & = langle Psi mid ({ hat {A}} { hat {B}} - { hat {A}} langle { hat {B}} rangle - { hat {B}} langle { hat {A}} rangle + langle { hat {A}} rangle langle { hat {B}} rangle) Psi rangle [4pt] & = langle Psi mid { hat {A}} { hat {B}} Psi rangle - langle Psi mid { hat {A}} langle { hat {B}} rangle Psi rangle - langle Psi mid { hat {B}} langle { hat {A}} rangle Psi rangle + langle Psi mid langle { hat {A}} rangle langle { hat {B}} rangle Psi rangle [4pt] & = langle { hat {A }} { hat {B}} rangle - langle { hat {A}} rangle langle { hat {B}} rangle - langle { hat {A}} rangle langle { hat {B}} rangle + langle { hat {A}} rangle langle { hat {B}} rangle [4pt] & = langle { hat {A}} { hat { B}} rangle - langle { hat {A}} rangle langle { hat {B}} rangle. End {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8c0c05428ab53be785878d1546c265c45c6e755)

![{ displaystyle langle f mid g rangle - langle g mid f rangle = langle { hat {A}} { hat {B}} rangle - langle { hat {A}} rangle langle { hat {B}} rangle - langle { hat {B}} { hat {A}} rangle + langle { hat {A}} rangle langle { hat {B }} rangle = langle [{ hat {A}}, { hat {B}}] rangle}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaf12a5caf8e73c4e1cfdfbbf3ebb1c3e32e7e0f)

![{ displaystyle | langle f mid g rangle | ^ {2} = { Big (} { frac {1} {2}} langle {{ hat {A}}, { hat {B) }} } rangle - langle { hat {A}} rangle langle { hat {B}} rangle { Big)} ^ {2} + { Big (} { frac {1} {2i}} langle [{ hat {A}}, { hat {B}}] rangle { Big)} ^ {2} ,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/074cd206c3b6789fd747fa2efa892ea596651470)
![{ displaystyle sigma _ {A} sigma _ {B} geq { sqrt {{ Big (} { frac {1} {2}} langle {{ hat {A}}, { шляпа {B}} } rangle - langle { hat {A}} rangle langle { hat {B}} rangle { Big)} ^ {2} + { Big (} { frac {1} {2i}} langle [{ hat {A}}, { hat {B}}] rangle { Big)} ^ {2}}}.}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/96a2a724edaa3e9b3e175f7de8158b796bef58c0)

![{ displaystyle sigma _ {A} ^ {2} sigma _ {B} ^ {2} geq left | { frac {1} {2}} operatorname {tr} ( rho {A, B }) - operatorname {tr} ( rho A) operatorname {tr} ( rho B) right | ^ {2} + left | { frac {1} {2i}} operatorname {tr } ( rho [A, B]) right | ^ {2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8271822251517d5a4e6879ea287fd36556a95e8)


![{ displaystyle sigma _ {A} ^ {2} + sigma _ {B} ^ {2} geq pm i langle Psi mid [A, B] | Psi rangle + mid langle Psi mid (A pm iB) mid { bar { Psi}} rangle | ^ {2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe87035b4463c5578ccda71d74b8e7c9fd627515)




![{ Displaystyle pm я langle Psi mid [A, B] mid Psi rangle}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a34a5250780e2a23b4befafff39d5522cc8266c)









![{ displaystyle [{ hat {x}}, { hat {p}}] = я hbar}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42dbbd0db710385288536bcf4f4a1b7cceb75d9a)


![{ displaystyle [J_ {x}, J_ {y}] = i hbar varepsilon _ {xyz} J_ {z}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92feb40a1e1bb732beffa55c687ccfbcec8ff007)







![[0,2 пи]](https://wikimedia.org/api/rest_v1/media/math/render/svg/348d40bf3f8b7e1c00c4346440d7e2e4f0cc9b91)
![{ Displaystyle { Hat {A}} psi ( theta) = theta psi ( theta), quad theta in [0,2 pi],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f85b2a63d69030bd4deabafe7641563413b8ec23)


![{ displaystyle [{ hat {A}}, { hat {B}}] = я hbar}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac8c6748f07eed66c5b329fcebdb8ca9d859ff71)





















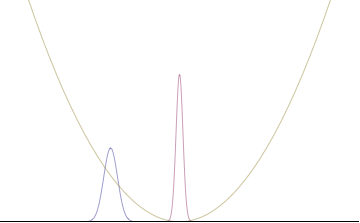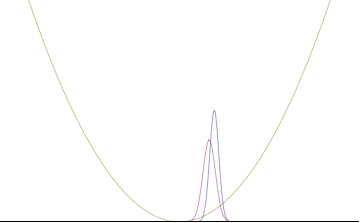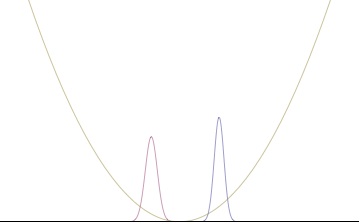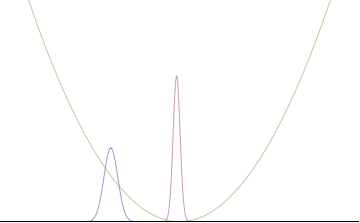








































![{ displaystyle varepsilon _ {A} , eta _ {B} + varepsilon _ {A} , sigma _ {B} + sigma _ {A} , eta _ {B} , geq , { frac {1} {2}} , left | langle [{ hat {A}}, { hat {B}}] rangle right |}](https://wikimedia.org/api/rest_v1/media/math/render/svg/507c66d05ec579594d36bbca8d92a3d2591a3145)
![{ displaystyle varepsilon _ {A} , eta _ {B} , geq , { frac {1} {2}} , left | langle [{ hat {A}}, { hat {B}}] rangle right |}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c0ac9415761d7b6ee02cba76450b3f36cc5568d)


![{ displaystyle varepsilon _ {A} , varepsilon _ {B} , geq , { frac {1} {2}} , left | langle [{ hat {A}}, { hat {B}}] rangle right |}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c40783a21b640620ef335dca2937ee9ac7aa9a50)
![{ displaystyle sigma _ {A} , sigma _ {B} , geq , { frac {1} {2}} , left | langle [{ hat {A}}, { hat {B}}] rangle right |}](https://wikimedia.org/api/rest_v1/media/math/render/svg/459f27fa54d560f33387b243214030b31e08d12b)
![{ displaystyle varepsilon _ {A} eta _ {B} + varepsilon _ {A} , sigma _ {B} + sigma _ {A} , eta _ {B} + sigma _ { A} sigma _ {B} geq left | langle [{ hat {A}}, { hat {B}}] rangle right |.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1dc1e7900ca212f157f381dda5fea49f2885ff78)
![{ displaystyle ( varepsilon _ {A} + sigma _ {A}) , ( eta _ {B} + sigma _ {B}) , geq , left | langle [{ hat {A}}, { hat {B}}] rangle right |.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/308a2567453272bef9b35660c39ab39513051e56)


![{ displaystyle { bar { varepsilon}} _ {A} , { bar { eta}} _ {B} , geq , left | langle [{ hat {A}}, { hat {B}}] rangle right |}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e6fd7cd1c81287fb8d7f07f732dd943c30114e7)

















![{ Displaystyle { begin {align} H_ {x} & = - int | psi (x) | ^ {2} ln (| psi (x) | ^ {2} cdot x_ {0}) , dx & = - { frac {1} {x_ {0} { sqrt {2 pi}}}} int _ {- infty} ^ { infty} exp { left (- { frac {x ^ {2}} {2x_ {0} ^ {2}}} right)} ln left [{ frac {1} { sqrt {2 pi}}} exp { left (- { frac {x ^ {2}} {2x_ {0} ^ {2}}} right)} right] , dx & = { frac {1} { sqrt {2 pi}}} int _ {- infty} ^ { infty} exp { left (- { frac {u ^ {2}} {2}} right)} left [ ln ({ sqrt {2 pi}}) + { frac {u ^ {2}} {2}} right] , du & = ln ({ sqrt {2 pi}}) + { frac {1} {2}}. End {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/124b7c9778e717ecae5fb23df17a3e6ea1cdab89)



![{ Displaystyle { begin {align} H_ {p} & = - int | varphi (p) | ^ {2} ln (| varphi (p) | ^ {2} cdot hbar / x_ { 0}) , dp & = - { sqrt { frac {2x_ {0} ^ {2}} { pi hbar ^ {2}}}} int _ {- infty} ^ { infty} exp { left (- { frac {2x_ {0} ^ {2} p ^ {2}} { hbar ^ {2}}} right)} ln left [{ sqrt { frac {2} { pi}}} exp { left (- { frac {2x_ {0} ^ {2} p ^ {2}} { hbar ^ {2}}} right)} right ] , dp & = { sqrt { frac {2} { pi}}} int _ {- infty} ^ { infty} exp { left (-2v ^ {2} right )} left [ ln left ({ sqrt { frac { pi} {2}}} right) + 2v ^ {2} right] , dv & = ln left ({ sqrt { frac { pi} {2}}} right) + { frac {1} {2}}. end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8106bc906d97851869d4000e4d3d0dd8e7916e56)

![{ Displaystyle OperatorName {P} [x_ {j}] = int _ {(j-1/2) delta xc} ^ {(j + 1/2) delta xc} | psi (x) | ^ {2} , dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7c173529c81593fd8c2e56a4e1af15f369c365c)
![{ displaystyle H_ {x} = - sum _ {j = - infty} ^ { infty} operatorname {P} [x_ {j}] ln operatorname {P} [x_ {j}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25c2fd9ede05e0615e6eff1a8f2ace626debd818)


![{ displaystyle { begin {align} operatorname {P} [x_ {j}] & = { sqrt { frac {m omega} { pi hbar}}} int _ {(j-1 / 2) delta x} ^ {(j + 1/2) delta x} exp left (- { frac {m omega x ^ {2}} { hbar}} right) , dx & = { sqrt { frac {1} { pi}}} int _ {(j-1/2) delta x { sqrt {m omega / hbar}}} ^ {(j + 1/2) delta x { sqrt {m omega / hbar}}} e ^ {u ^ {2}} , du & = { frac {1} {2}} left [ имя оператора {erf} left ( left (j + { frac {1} {2}} right) delta x cdot { sqrt { frac {m omega} { hbar}}} right) - operatorname {erf} left ( left (j - { frac {1} {2}} right) delta x cdot { sqrt { frac {m omega} { hbar}}} right ) right] end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb98a69e46b2d10143459959d1679c78443b6378)
![{ displaystyle operatorname {P} [p_ {j}] = { frac {1} {2}} left [ operatorname {erf} left ( left (j + { frac {1} {2}}) right) delta p cdot { frac {1} { sqrt { hbar m omega}}} right) - operatorname {erf} left ( left (j - { frac {1} { 2}} right) delta x cdot { frac {1} { sqrt { hbar m omega}}} right) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed784fa900105bac03e1163a54fc3dd5732367aa)


![{ displaystyle operatorname {P} [x_ {j}] = operatorname {P} [p_ {j}] = { frac {1} {2}} left [ operatorname {erf} left ( left (j + { frac {1} {2}} right) { sqrt {2 pi}} right) - operatorname {erf} left ( left (j - { frac {1} {2} } right) { sqrt {2 pi}} right) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba65e2143152330bf233c24e6524ac16a365c168)
![{ displaystyle { begin {align} H_ {x} = H_ {p} & = - sum _ {j = - infty} ^ { infty} operatorname {P} [x_ {j}] ln имя оператора {P} [x_ {j}] & = - sum _ {j = - infty} ^ { infty} { frac {1} {2}} left [ operatorname {erf} left ( left (j + { frac {1} {2}} right) { sqrt {2 pi}} right) - operatorname {erf} left ( left (j - { frac {1}) {2}} right) { sqrt {2 pi}} right) right] ln { frac {1} {2}} left [ operatorname {erf} left ( left (j + { frac {1} {2}} right) { sqrt {2 pi}} right) - operatorname {erf} left ( left (j - { frac {1} {2}} right ) { sqrt {2 pi}} right) right] & приблизительно 0,3226 end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7edfbe77762479a164b5863aa0f72ef098e1df08)

![{ displaystyle psi (x) = { begin {cases} { frac {1} { sqrt {2a}}} & { text {for}} | x | leq a, [8pt] 0 & { text {for}} | x |> a end {case}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea3f0b2acef217f888c5fe38d2985169b925da48)

![{ displaystyle operatorname {P} [x_ {0}] = int _ {- a} ^ {0} { frac {1} {2a}} , dx = { frac {1} {2}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bb8e8e07cba14e44ac3fd1f812c87b344f79978)
![{ displaystyle operatorname {P} [x_ {1}] = int _ {0} ^ {a} { frac {1} {2a}} , dx = { frac {1} {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abb619286fac29cd04fb8ad539e4d7fc979da3fd)
![{ displaystyle H_ {x} = - sum _ {j = 0} ^ {1} operatorname {P} [x_ {j}] ln operatorname {P} [x_ {j}] = - { frac {1} {2}} ln { frac {1} {2}} - { frac {1} {2}} ln { frac {1} {2}} = ln 2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd49a257fd5578026bd28e8e539dccfaae24dd1f)
![{ displaystyle { begin {align} operatorname {P} [p_ {j}] & = { frac {a} { pi hbar}} int _ {(j-1/2) delta p} ^ {(j + 1/2) delta p} operatorname {sinc} ^ {2} left ({ frac {ap} { hbar}} right) , dp & = { frac { 1} { pi}} int _ {2 pi (j-1/2)} ^ {2 pi (j + 1/2)} operatorname {sinc} ^ {2} (u) , du & = { frac {1} { pi}} left [ operatorname {Si} ((4j + 2) pi) - operatorname {Si} ((4j-2) pi) right] конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c11b911bee6171d2a7ac1ee1c5522d49625ffb2)
![{ displaystyle H_ {p} = - sum _ {j = - infty} ^ { infty} operatorname {P} [p_ {j}] ln operatorname {P} [p_ {j}] = - operatorname {P} [p_ {0}] ln operatorname {P} [p_ {0}] - 2 cdot sum _ {j = 1} ^ { infty} operatorname {P} [p_ {j }] ln operatorname {P} [p_ {j}] приблизительно 0,53}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae44da862dea854275b063fc3b5fe01bd3f3309f)


![{ displaystyle left [{ hat {A}}, { hat {B}} right] = { hat {C}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/776f576b13fa60d2828ef9d35d620d01b9826710)



![{ displaystyle left [ sigma _ {i}, sigma _ {k} right] = , i , e_ {ikl} sigma _ {l},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e519dea165eb5aa82f72f4c00b9a34d4b3fb28a)








![{ displaystyle { hat {C}} _ {2} = i left [ delta { hat {B}}, { hat {C}} right], qquad { hat {C}} _ {3} = i left [ delta { hat {A}}, { hat {C}} right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea074dcfe994c9e7ca4c52d8410111a6d43df472)















































