WikiDer > Декартов тензор

Два разных 3d ортонормированные базы: каждый базис состоит из взаимно перпендикулярных единичных векторов.

В геометрия и линейная алгебра, а Декартов тензор использует ортонормированный базис к представлять а тензор в Евклидово пространство в виде компонентов. Преобразование компонентов тензора из одного такого базиса в другой осуществляется через ортогональное преобразование.

Наиболее известные системы координат - это двумерный и трехмерный Декартова координата системы. Декартовы тензоры могут использоваться с любым евклидовым пространством или, более технически, с любым конечномерным пространством. векторное пространство над поле из действительные числа который имеет внутренний продукт.

Использование декартовых тензоров происходит в физика и инженерное дело, например, с Тензор напряжений Коши и момент инерции тензор в динамика твердого тела. Иногда вообще криволинейные координаты удобны, так как в высокодеформируемых механика сплошной среды, или даже необходимо, как в общая теория относительности. Хотя ортонормированные основы могут быть найдены для некоторых таких систем координат (например, касательная к сферические координаты), Декартовы тензоры могут значительно упростить приложения, в которых достаточно вращения прямолинейных осей координат. Преобразование - это пассивное преобразование, поскольку меняются координаты, а не физическая система.

Декартова основа и соответствующая терминология

Векторы в трех измерениях

В 3D Евклидово пространство, ℝ³, то стандартная основа является е_Икс, е_у, е_z. Каждый базисный вектор указывает на оси x, y и z, и все векторы единичные векторы (или нормализованный), поэтому базис ортонормированный.

На всем протяжении, говоря о Декартовы координаты в три измерения, предполагается правосторонняя система, и на практике это гораздо чаще, чем левосторонняя система, см. ориентация (векторное пространство) для подробностей.

Для декартовых тензоров порядка 1 декартов вектор а может быть записано алгебраически как линейная комбинация базисных векторов е_Икс, е_у, е_z:

${ displaystyle mathbf {a} = a _ { text {x}} mathbf {e} _ { text {x}} + a _ { text {y}} mathbf {e} _ { text {y }} + _ { text {z}} mathbf {e} _ { text {z}}}$

где координаты вектора относительно декартового базиса обозначаются а_Икс, а_у, а_z. Обычно и полезно отображать базисные векторы как вектор-столбец

${ displaystyle mathbf {e} _ { text {x}} = { begin {pmatrix} 1 0 0 end {pmatrix}} ,, quad mathbf {e} _ { text {y}} = { begin {pmatrix} 0 1 0 end {pmatrix}} ,, quad mathbf {e} _ { text {z}} = { begin {pmatrix} 0 0 1 end {pmatrix}}}$

когда у нас есть вектор координат в векторном представлении столбца:

${ displaystyle mathbf {a} = { begin {pmatrix} a _ { text {x}} a _ { text {y}} a _ { text {z}} end {pmatrix}}}$

А вектор строки представление также является законным, хотя в контексте общих криволинейных систем координат представления векторов строк и столбцов используются отдельно по определенным причинам - см. Обозначения Эйнштейна и ковариация и контравариантность векторов для чего.

Термин «компонент» вектора неоднозначен: он может относиться к:

• конкретная координата вектора, например а_z (скаляр), и аналогично для Икс и у, или же
• координатный скаляр, умножающий соответствующий базисный вектор, и в этом случае "y-компонента" а является а_уе_у (вектор), и аналогично для Икс и z.

Более общие обозначения обозначение тензорного индекса, который имеет гибкость числовых значений, а не фиксированных меток координат. Декартовы метки заменяются тензорными индексами в базисных векторах е_Икс ↦ е₁, е_у ↦ е₂, е_z ↦ е₃ и координаты а_Икс ↦ а₁, а_у ↦ а₂, а_z ↦ а₃. В общем, обозначения е₁, е₂, е₃ относится к любой основа, и а₁, а₂, а₃ относится к соответствующей системе координат; хотя здесь они ограничены декартовой системой. Потом:

${ displaystyle mathbf {a} = a_ {1} mathbf {e} _ {1} + a_ {2} mathbf {e} _ {2} + a_ {3} mathbf {e} _ {3} = sum _ {i = 1} ^ {3} a_ {i} mathbf {e} _ {i}}$

Стандартно использовать Обозначения Эйнштейна- знак суммирования по индексу, который присутствует ровно дважды в пределах члена, может быть опущен для краткости обозначений:

${ displaystyle mathbf {a} = sum _ {i = 1} ^ {3} a_ {i} mathbf {e} _ {i} Equiv a_ {i} mathbf {e} _ {i}}$

Преимущество индексной нотации перед обозначениями, специфичными для координат, заключается в независимости размерности лежащего в основе векторного пространства, то есть одно и то же выражение в правой части принимает ту же форму в более высоких измерениях (см. Ниже). Ранее декартовы метки x, y, z были просто метками и нет индексы. (Неофициально сказать "я = x, y, z ").

Тензоры второго порядка в трех измерениях

А диадический тензор Т - тензор порядка 2, образованный тензорное произведение ⊗ двух декартовых векторов а и б, написано Т = а ⊗ б. Аналогично векторам его можно записать как линейную комбинацию тензорного базиса е_Икс ⊗ е_Икс ≡ е_хх, е_Икс ⊗ е_у ≡ е_ху, ..., е_z ⊗ е_z ≡ е_zz (правая часть каждого идентификатора - это всего лишь аббревиатура, не более того):

${ displaystyle { begin {array} {ccl} mathbf {T} & = & left (a _ { text {x}} mathbf {e} _ { text {x}} + a _ { text { y}} mathbf {e} _ { text {y}} + a _ { text {z}} mathbf {e} _ { text {z}} right) otimes left (b _ { text {x}} mathbf {e} _ { text {x}} + b _ { text {y}} mathbf {e} _ { text {y}} + b _ { text {z}} mathbf {e} _ { text {z}} right) && & = & a _ { text {x}} b _ { text {x}} mathbf {e} _ { text {x}} otimes mathbf {e} _ { text {x}} + a _ { text {x}} b _ { text {y}} mathbf {e} _ { text {x}} otimes mathbf { e} _ { text {y}} + a _ { text {x}} b _ { text {z}} mathbf {e} _ { text {x}} otimes mathbf {e} _ { текст {z}} && {} + a _ { text {y}} b _ { text {x}} mathbf {e} _ { text {y}} otimes mathbf {e} _ { текст {x}} + a _ { text {y}} b _ { text {y}} mathbf {e} _ { text {y}} otimes mathbf {e} _ { text {y}} + a _ { text {y}} b _ { text {z}} mathbf {e} _ { text {y}} otimes mathbf {e} _ { text {z}} && {} + a _ { text {z}} b _ { text {x}} mathbf {e} _ { text {z}} otimes mathbf {e} _ { text {x}} + a _ { text {z}} b _ { text {y}} mathbf {e} _ { text {z}} otimes mathbf {e} _ { text {y}} + a _ { text {z}} b_ { text {z}} mathbf {e} _ { text {z}} ot imes mathbf {e} _ { text {z}} end {array}}}$

Представление каждого базисного тензора в виде матрицы:

${ displaystyle { mathbf {e} _ { text {x}} otimes mathbf {e} _ { text {x}}} Equiv mathbf {e} _ { text {xx}} = { begin {pmatrix} 1 & 0 & 0 0 & 0 & 0 0 & 0 & 0 end {pmatrix}} ,, quad { mathbf {e} _ { text {x}} otimes mathbf {e} _ { text {y }}} Equiv mathbf {e} _ { text {xy}} = { begin {pmatrix} 0 & 1 & 0 0 & 0 & 0 0 & 0 & 0 end {pmatrix}} ,, cdots quad { mathbf {e } _ { text {z}} otimes mathbf {e} _ { text {z}}} Equiv mathbf {e} _ { text {zz}} = { begin {pmatrix} 0 & 0 & 0 0 & 0 & 0 0 & 0 & 1 end {pmatrix}}}$

тогда Т более систематично можно представить в виде матрицы:

${ displaystyle mathbf {T} = { begin {pmatrix} a _ { text {x}} b _ { text {x}} & a _ { text {x}} b _ { text {y}} & a _ { text {x}} b _ { text {z}} a _ { text {y}} b _ { text {x}} & a _ { text {y}} b _ { text {y}} & a _ { text {y}} b _ { text {z}} a _ { text {z}} b _ { text {x}} & a _ { text {z}} b _ { text {y}} & a _ { текст {z}} b _ { text {z}} end {pmatrix}}}$

Видеть матричное умножение для обозначения соответствия между матрицами и скалярными и тензорными произведениями.

В более общем плане, независимо от того, Т представляет собой тензорное произведение двух векторов, это всегда линейная комбинация базисных тензоров с координатами Т_хх, Т_ху, ... Т_zz:

${ displaystyle { begin {array} {ccl} mathbf {T} & = & T _ { text {xx}} mathbf {e} _ { text {xx}} + T _ { text {xy}} mathbf {e} _ { text {xy}} + T _ { text {xz}} mathbf {e} _ { text {xz}} && {} + T _ { text {yx}} mathbf {e} _ { text {yx}} + T _ { text {yy}} mathbf {e} _ { text {yy}} + T _ { text {yz}} mathbf {e} _ { текст {yz}} && {} + T _ { text {zx}} mathbf {e} _ { text {zx}} + T _ { text {zy}} mathbf {e} _ { text {zy}} + T _ { text {zz}} mathbf {e} _ { text {zz}} end {array}}}$

а в терминах тензорных индексов:

${ Displaystyle mathbf {T} = T_ {ij} mathbf {e} _ {ij} Equiv sum _ {ij} T_ {ij} mathbf {e} _ {i} otimes mathbf {e} _ {j} ,,}$

и в матричной форме:

${ displaystyle mathbf {T} = { begin {pmatrix} T _ { text {xx}} & T _ { text {xy}} & T _ { text {xz}} T _ { text {yx}} & T_ { text {yy}} & T _ { text {yz}} T _ { text {zx}} & T _ { text {zy}} & T _ { text {zz}} end {pmatrix}}}$

Тензоры второго порядка естественным образом встречаются в физике и технике, когда физические величины имеют направленную зависимость в системе, часто по принципу «стимул-реакция». Математически это можно увидеть через один аспект тензоров - они полилинейные функции. Тензор второго порядка Т который принимает вектор ты некоторой величины и направления вернет вектор v; другой величины и в другом направлении ты, в целом. Обозначения, используемые для функции в математический анализ заставляет нас писать v = Т(ты),^[1] в то время как та же идея может быть выражена в матричных и индексных обозначениях^[2] (включая соглашение о суммировании), соответственно:

${ displaystyle { begin {pmatrix} v _ { text {x}} v _ { text {y}} v _ { text {z}} end {pmatrix}} = { begin {pmatrix} T _ { text {xx}} & T _ { text {xy}} & T _ { text {xz}} T _ { text {yx}} & T _ { text {yy}} & T _ { text {yz}} T _ { text {zx}} & T _ { text {zy}} & T _ { text {zz}} end {pmatrix}} { begin {pmatrix} u _ { text {x}} u_ { text {y}} u _ { text {z}} end {pmatrix}} ,, quad v_ {i} = T_ {ij} u_ {j}}$

Под «линейным», если ты = ρр + σs для двух скаляров ρ и σ и векторы р и s, затем в обозначениях функций и индексов:

${ Displaystyle mathbf {v} = mathbf {T} ( rho mathbf {r} + sigma mathbf {s}) = rho mathbf {T} ( mathbf {r}) + sigma mathbf {T} ( mathbf {s})}$

${ displaystyle v_ {i} = T_ {ij} ( rho r_ {j} + sigma s_ {j}) = rho T_ {ij} r_ {j} + sigma T_ {ij} s_ {j}}$

и аналогично для матричных обозначений. Обозначения функций, матриц и индексов означают одно и то же. Матричные формы обеспечивают четкое отображение компонентов, а индексная форма позволяет упростить тензорно-алгебраические манипуляции с формулами в компактной форме. Оба обеспечивают физическую интерпретацию направления; векторы имеют одно направление, а тензоры второго порядка соединяют два направления вместе. Можно связать тензорный индекс или координатную метку с направлением базисного вектора.

Использование тензоров второго порядка является минимумом для описания изменений величин и направлений векторов, поскольку скалярное произведение двух векторов всегда является скаляром, а перекрестное произведение двух векторов всегда является псевдовектором, перпендикулярным плоскости, определяемой векторами, поэтому эти произведения векторов сами по себе не могут получить новый вектор любой величины в любом направлении. (См. Также информацию о скалярных произведениях и перекрестных произведениях ниже). Тензорное произведение двух векторов - это тензор второго порядка, хотя сам по себе он не имеет очевидной направленной интерпретации.

Предыдущую мысль можно продолжить: если Т принимает два вектора п и q, он вернет скаляр р. В обозначениях функций пишем р = Т(п, q), а в матричных и индексных обозначениях (включая соглашение о суммировании) соответственно:

${ displaystyle r = { begin {pmatrix} p _ { text {x}} & p _ { text {y}} & p _ { text {z}} end {pmatrix}} { begin {pmatrix} T _ { текст {xx}} & T _ { text {xy}} & T _ { text {xz}} T _ { text {yx}} & T _ { text {yy}} & T _ { text {yz}} T_ { text {zx}} & T _ { text {zy}} & T _ { text {zz}} end {pmatrix}} { begin {pmatrix} q _ { text {x}} q _ { text { y}} q _ { text {z}} end {pmatrix}} ,, quad r = p_ {i} T_ {ij} q_ {j}}$

Тензор Т линейна по обоим входным векторам. Когда векторы и тензоры записываются без ссылки на компоненты, а индексы не используются, иногда точка · ставится там, где суммирование по индексам (известное как тензорные сокращения) принимаются. Для вышеуказанных случаев:^[1][2]

${ Displaystyle mathbf {v} = mathbf {T} cdot mathbf {u}}$

${ Displaystyle г = mathbf {p} cdot mathbf {T} cdot mathbf {q}}$

мотивировано обозначением скалярного произведения:

${ displaystyle mathbf {a} cdot mathbf {b} Equiv a_ {i} b_ {i}}$

В более общем смысле тензор порядка м который принимает п векторы (где п находится между 0 и м включительно) вернет тензор порядка м − п, видеть Тензор: как полилинейные карты для дальнейших обобщений и деталей. Приведенные выше концепции также применимы к псевдовекторам так же, как и к векторам. Сами векторы и тензоры могут меняться в пределах пространства, и в этом случае мы имеем векторные поля и тензорные поля, а также может зависеть от времени.

Вот несколько примеров:

Примененный или данный ...	... к материалу или объекту ...	... приводит к ...	... в материале или объекте, определяемом:
единичный вектор п	Тензор напряжений Коши σ	тяговая сила т	${ displaystyle mathbf {t} = { boldsymbol { sigma}} cdot mathbf {n}}$
угловая скорость ω	момент инерции я	ан угловой момент J	${ displaystyle mathbf {J} = mathbf {I} cdot { boldsymbol { omega}}}$
	момент инерции я	вращающийся кинетическая энергия Т	${ displaystyle T = { frac {1} {2}} { boldsymbol { omega}} cdot mathbf {I} cdot { boldsymbol { omega}}}$
электрическое поле E	электрическая проводимость σ	а плотность тока поток J	${ Displaystyle mathbf {J} = { boldsymbol { sigma}} cdot mathbf {E}}$
	поляризуемость α (связанный с диэлектрическая проницаемость ε и электрическая восприимчивость χE)	индуцированный поляризация поле п	${ Displaystyle mathbf {P} = { boldsymbol { alpha}} cdot mathbf {E}}$
магнитный ЧАС поле	магнитная проницаемость μ	а магнитный B поле	${ Displaystyle mathbf {B} = { boldsymbol { mu}} cdot mathbf {H}}$

В примере с электропроводностью индексные и матричные обозначения будут следующими:

${ Displaystyle J_ {i} = sigma _ {ij} E_ {j} Equiv sum _ {j} sigma _ {ij} E_ {j}}$

${ displaystyle { begin {pmatrix} J _ { text {x}} J _ { text {y}} J _ { text {z}} end {pmatrix}} = { begin {pmatrix} sigma _ { text {xx}} & sigma _ { text {xy}} & sigma _ { text {xz}} sigma _ { text {yx}} & sigma _ { текст {yy}} & sigma _ { text {yz}} sigma _ { text {zx}} & sigma _ { text {zy}} & sigma _ { text {zz}} end {pmatrix}} { begin {pmatrix} E _ { text {x}} E _ { text {y}} E _ { text {z}} end {pmatrix}}}$

а для вращательной кинетической энергии Т:

${ displaystyle T = { frac {1} {2}} omega _ {i} I_ {ij} omega _ {j} Equiv { frac {1} {2}} sum _ {ij} омега _ {i} I_ {ij} omega _ {j} ,,}$

${ displaystyle T = { frac {1} {2}} { begin {pmatrix} omega _ { text {x}} & omega _ { text {y}} & omega _ { text { z}} end {pmatrix}} { begin {pmatrix} I _ { text {xx}} & I _ { text {xy}} & I _ { text {xz}} I _ { text {yx}} & I_ { text {yy}} & I _ { text {yz}} I _ { text {zx}} & I _ { text {zy}} & I _ { text {zz}} end {pmatrix}} { begin {pmatrix} omega _ { text {x}} omega _ { text {y}} omega _ { text {z}} end {pmatrix}} ,.}$

Смотрите также конститутивное уравнение для более специализированных примеров.

Векторы и тензоры в п размеры

В п-мерное евклидово пространство над действительными числами, ℝ^п, стандартный базис обозначается е₁, е₂, е₃, ... е_п. Каждый базисный вектор е_я указывает на положительные Икс_я оси с ортонормированным основанием. Компонент j из е_я дается Дельта Кронекера:

${ displaystyle ( mathbf {e} _ {i}) _ {j} = delta _ {ij}}$

Вектор в ℝ^п принимает форму:

${ displaystyle mathbf {a} = a_ {i} mathbf {e} _ {i} Equiv sum _ {i} a_ {i} mathbf {e} _ {i} ,.}$

Аналогично для тензора порядка 2 выше для каждого вектора а и б в ℝ^п:

${ displaystyle mathbf {T} = a_ {i} b_ {j} mathbf {e} _ {ij} Equiv sum _ {ij} a_ {i} b_ {j} mathbf {e} _ {i } otimes mathbf {e} _ {j} ,,}$

или в более общем плане:

${ Displaystyle mathbf {T} = T_ {ij} mathbf {e} _ {ij} Equiv sum _ {ij} T_ {ij} mathbf {e} _ {i} otimes mathbf {e} _ {j} ,.}$

Преобразования декартовых векторов (любое количество измерений)

Такой же вектор положения Икс представлены в двух трехмерных прямоугольных системах координат, каждая с ортонормированный базис, кубоиды иллюстрируют закон параллелограмма для добавления компонентов вектора.

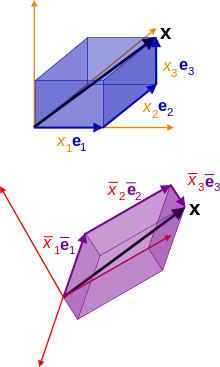
Значение «инвариантности» относительно преобразований координат

В вектор положения Икс в ℝ^п это простой и распространенный пример вектора, который может быть представлен в любой система координат. Рассмотрим случай прямоугольные системы координат только с ортонормированными основаниями. Можно иметь систему координат с прямоугольной геометрией, если все базисные векторы взаимно перпендикулярны и не нормализованы, и в этом случае базис ортогонал но не ортонормальный. Однако ортонормированными базами легче манипулировать, и они часто используются на практике. Следующие результаты верны для ортонормированных, а не ортогональных базисов.

В одной прямоугольной системе координат Икс как контрагент имеет координаты Икс^я и базисные векторы е_я, а как ковектор имеет координаты Икс_я и базисные ковекторы е^я, и у нас есть:

${ displaystyle mathbf {x} = x ^ {i} mathbf {e} _ {i} ,, quad mathbf {x} = x_ {i} mathbf {e} ^ {i}}$

В другой прямоугольной системе координат Икс как контрагент имеет координаты Икс^я и базы е_я, а как ковектор имеет координаты Икс_я и базы е^я, и у нас есть:

${ displaystyle mathbf {x} = { bar {x}} ^ {i} { bar { mathbf {e}}} _ {i} ,, quad mathbf {x} = { bar { x}} _ {i} { bar { mathbf {e}}} ^ {i}}$

Каждая новая координата является функцией всех старых, и наоборот для обратная функция:

${ displaystyle { bar {x}} {} ^ {i} = { bar {x}} {} ^ {i} left (x ^ {1}, x ^ {2}, cdots right) quad rightleftharpoons quad x {} ^ {i} = x {} ^ {i} left ({ bar {x}} ^ {1}, { bar {x}} ^ {2}, cdots верно)}$

${ displaystyle { bar {x}} {} _ {i} = { bar {x}} {} _ {i} left (x_ {1}, x_ {2}, cdots right) quad rightleftharpoons quad x {} _ {i} = x {} _ {i} left ({ bar {x}} _ {1}, { bar {x}} _ {2}, cdots right )}$

и аналогично каждый новый базисный вектор является функцией всех старых, и наоборот для обратной функции:

${ displaystyle { bar { mathbf {e}}} {} _ {j} = { bar { mathbf {e}}} {} _ {j} left ( mathbf {e} _ {1} , mathbf {e} _ {2} cdots right) quad rightleftharpoons quad mathbf {e} {} _ {j} = mathbf {e} {} _ {j} left ({ bar { mathbf {e}}} _ {1}, { bar { mathbf {e}}} _ {2} cdots right)}$

${ displaystyle { bar { mathbf {e}}} {} ^ {j} = { bar { mathbf {e}}} {} ^ {j} left ( mathbf {e} ^ {1} , mathbf {e} ^ {2} cdots right) quad rightleftharpoons quad mathbf {e} {} ^ {j} = mathbf {e} {} ^ {j} left ({ bar { mathbf {e}}} ^ {1}, { bar { mathbf {e}}} ^ {2} cdots right)}$

для всех я, j.

Вектор инвариантен при любой смене базиса, поэтому если координаты преобразуются в соответствии с матрица преобразования L, базы преобразуются согласно матрица обратная L⁻¹, и наоборот, если координаты преобразуются по обратному L⁻¹, базы преобразуются по матрице L. Разница между каждым из этих преобразований обычно отображается с помощью индексов в виде верхних индексов для контравариантности и нижних индексов для ковариации, а координаты и основания - линейно преобразованный по следующим правилам:

Векторные элементы	Контравариантный закон преобразования	Ковариантный закон преобразования
Координаты	${ displaystyle { bar {x}} ^ {j} = x ^ {i} ({ boldsymbol { mathsf {L}}}) _ {i} {} ^ {j} = x ^ {i} { mathsf {L}} _ {i} {} ^ {j}}$	${ displaystyle { bar {x}} _ {j} = x_ {k} ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {j} {} ^ {k}}$
Основа	${ displaystyle { bar { mathbf {e}}} _ {j} = ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {j} {} ^ {k} mathbf { e} _ {k}}$	${ displaystyle { bar { mathbf {e}}} ^ {j} = ({ boldsymbol { mathsf {L}}}) _ {i} {} ^ {j} mathbf {e} ^ {i } = { mathsf {L}} _ {i} {} ^ {j} mathbf {e} ^ {i}}$
Любой вектор	${ displaystyle { bar {x}} ^ {j} { bar { mathbf {e}}} _ {j} = x ^ {i} { mathsf {L}} _ {i} {} ^ { j} ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {j} {} ^ {k} mathbf {e} _ {k} = x ^ {i} delta _ {i } {} ^ {k} mathbf {e} _ {k} = x ^ {i} mathbf {e} _ {i}}$	${ displaystyle { bar {x}} _ {j} { bar { mathbf {e}}} ^ {j} = x_ {i} ({ boldsymbol { mathsf {L}}} ^ {- 1 }) _ {j} {} ^ {i} { mathsf {L}} _ {k} {} ^ {j} mathbf {e} ^ {k} = x_ {i} delta ^ {i} { } _ {k} mathbf {e} ^ {k} = x_ {i} mathbf {e} ^ {i}}$

где L_я^j представляет записи матрица преобразования (номер строки я и номер столбца j) и (L⁻¹)_я^k обозначает записи обратная матрица матрицы L_я^k.

Если L является ортогональное преобразование (ортогональная матрица), преобразующиеся им объекты определяются как Декартовы тензоры. Это геометрически имеет интерпретацию, что прямоугольная система координат отображается в другую прямоугольную систему координат, в которой норма вектора Икс сохраняется (и расстояния сохраняются).

В детерминант из L это det (L) = ± 1, что соответствует двум типам ортогональных преобразований: (+1) для вращения и (−1) для неправильные вращения (включая размышления).

Имеются значительные алгебраические упрощения, матрица транспонировать это обратный из определения ортогонального преобразования:

${ displaystyle { boldsymbol { mathsf {L}}} ^ { mathrm {T}} = { boldsymbol { mathsf {L}}} ^ {- 1} Rightarrow ({ boldsymbol { mathsf {L }}} ^ {- 1}) _ {i} {} ^ {j} = ({ boldsymbol { mathsf {L}}} ^ { mathrm {T}}) _ {i} {} ^ {j } = ({ boldsymbol { mathsf {L}}}) ^ {j} {} _ {i} = { mathsf {L}} ^ {j} {} _ {i}}$

Из предыдущей таблицы ортогональные преобразования ковекторов и контравекторов идентичны. Нет необходимости различать повышение и понижение показателей, и в этом контексте и в приложениях к физике и технике все индексы обычно имеют нижние индексы, чтобы исключить путаницу для экспоненты. В оставшейся части статьи все индексы будут понижены. Фактические повышенные и пониженные индексы можно определить, рассмотрев, какие количества являются ковекторами или контравекторами, а также соответствующими правилами преобразования.

Точно такие же правила преобразования применяются к любому вектору а, а не только вектор положения. Если его компоненты а_я не трансформируйте по правилам, а не вектор.

Несмотря на схожесть приведенных выше выражений, для изменения координат, таких как Икс^j = L_я^jИкс^я, а действие тензора на вектор вида б_я = Т_ijа_j, L не тензор, но Т является. При смене координат L это матрица, используется для связи двух прямоугольных систем координат с ортонормированными основаниями. Для тензора, связывающего вектор с вектором, векторы и тензоры во всем уравнении принадлежат одной и той же системе координат и базису.

Производные и матричные элементы Якоби

Записи L находятся частные производные новых или старых координат относительно старых или новых координат соответственно.

Дифференцировать Икс_я относительно Икс_k:

${ displaystyle { frac { partial { bar {x}} _ {i}} { partial x_ {k}}} = { frac { partial} { partial x_ {k}}} (x_ { j} { mathsf {L}} _ {ji}) = { mathsf {L}} _ {ji} { frac { partial x_ {j}} { partial x_ {k}}} = delta _ {kj} { mathsf {L}} _ {ji} = { mathsf {L}} _ {ki}}$

так

${ displaystyle { mathsf {L}} _ {i} {} ^ {j} Equiv { mathsf {L}} _ {ij} = { frac { partial { bar {x}} _ {j }} { partial x_ {i}}}}$

является элементом Матрица якобиана. Существует (частично мнемоническое) соответствие между индексными позициями, прикрепленными к L и в частной производной: я наверху и j внизу, в каждом случае, хотя для декартовых тензоров индексы могут быть понижены.

И наоборот, дифференцируя Икс_j относительно Икс_я:

${ displaystyle { frac { partial x_ {j}} { partial { bar {x}} _ {k}}} = { frac { partial} { partial { bar {x}} _ { k}}} ({ bar {x}} _ {i} ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {ij}) = { frac { partial { bar { x}} _ {i}} { partial { bar {x}} _ {k}}} ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {ij} = delta _ {ki} ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {ij} = ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {kj}}$

так

${ displaystyle ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {i} {} ^ {j} Equiv ({ boldsymbol { mathsf {L}}} ^ {- 1} ) _ {ij} = { frac { partial x_ {j}} { partial { bar {x}} _ {i}}}}$

является элементом обратной матрицы Якоби с аналогичным индексным соответствием.

Во многих источниках преобразования формулируются в терминах частных производных:

а явные матричные уравнения в 3d следующие:

${ displaystyle { bar { mathbf {x}}} = { boldsymbol { mathsf {L}}} mathbf {x}}$

${ displaystyle { begin {pmatrix} { bar {x}} _ {1} { bar {x}} _ {2} { bar {x}} _ {3} end {pmatrix }} = { begin {pmatrix} { frac { partial { bar {x}} _ {1}} { partial x_ {1}}} & { frac { partial { bar {x}} _ {1}} { partial x_ {2}}} & { frac { partial { bar {x}} _ {1}} { partial x_ {3}}} { frac { partial { bar {x}} _ {2}} { partial x_ {1}}} & { frac { partial { bar {x}} _ {2}} { partial x_ {2}}} & { frac { partial { bar {x}} _ {2}} { partial x_ {3}}} { frac { partial { bar {x}} _ {3}} { partial x_ {1}}} & { frac { partial { bar {x}} _ {3}} { partial x_ {2}}} & { frac { partial { bar {x}} _ { 3}} { partial x_ {3}}} end {pmatrix}} { begin {pmatrix} x_ {1} x_ {2} x_ {3} end {pmatrix}}}$

аналогично для

${ displaystyle mathbf {x} = { boldsymbol { mathsf {L}}} ^ {- 1} { bar { mathbf {x}}} = { boldsymbol { mathsf {L}}} ^ { mathrm {T}} { bar { mathbf {x}}}}$

Проекции по координатным осям

Вершина: Углы от Икс_я оси к Икс_я топоры. Нижний: Наоборот.

Как и все линейные преобразования, L зависит от выбранной основы. Для двух ортонормированных баз

${ displaystyle { bar { mathbf {e}}} _ {i} cdot { bar { mathbf {e}}} _ {j} = mathbf {e} _ {i} cdot mathbf { e} _ {j} = delta _ {ij} ,, quad left | mathbf {e} _ {i} right | = left | { bar { mathbf {e}}} _ { i} right | = 1 ,,}$

• проектирование Икс к Икс оси: ${ displaystyle { bar {x}} _ {i} = { bar { mathbf {e}}} _ {i} cdot mathbf {x} = { bar { mathbf {e}}} _ {i} cdot x_ {j} mathbf {e} _ {j} = x_ {i} { mathsf {L}} _ {ij} ,,}$
• проектирование Икс к Икс оси: ${ displaystyle x_ {i} = mathbf {e} _ {i} cdot mathbf {x} = mathbf {e} _ {i} cdot { bar {x}} _ {j} { bar { mathbf {e}}} _ {j} = { bar {x}} _ {j} ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {ji} ,.}$

Следовательно, компоненты сводятся к направляющие косинусы между Икс_я и Икс_j оси:

${ displaystyle { mathsf {L}} _ {ij} = { bar { mathbf {e}}} _ {i} cdot mathbf {e} _ {j} = cos theta _ {ij} }$

${ displaystyle ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {ij} = mathbf {e} _ {i} cdot { bar { mathbf {e}}} _ { j} = cos theta _ {ji}}$

куда θ_ij и θ_джи углы между Икс_я и Икс_j топоры. В целом, θ_ij не равно θ_джи, потому что например θ₁₂ и θ₂₁ это два разных угла.

Преобразование координат можно записать:

а явные матричные уравнения в 3d следующие:

${ displaystyle { bar { mathbf {x}}} = { boldsymbol { mathsf {L}}} mathbf {x}}$

${ displaystyle { begin {pmatrix} { bar {x}} _ {1} { bar {x}} _ {2} { bar {x}} _ {3} end {pmatrix }} = { begin {pmatrix} { bar { mathbf {e}}} _ {1} cdot mathbf {e} _ {1} & { bar { mathbf {e}}} _ {1 } cdot mathbf {e} _ {2} & { bar { mathbf {e}}} _ {1} cdot mathbf {e} _ {3} { bar { mathbf {e} }} _ {2} cdot mathbf {e} _ {1} & { bar { mathbf {e}}} _ {2} cdot mathbf {e} _ {2} & { bar { mathbf {e}}} _ {2} cdot mathbf {e} _ {3} { bar { mathbf {e}}} _ {3} cdot mathbf {e} _ {1} & { bar { mathbf {e}}} _ {3} cdot mathbf {e} _ {2} & { bar { mathbf {e}}} _ {3} cdot mathbf {e} _ {3} end {pmatrix}} { begin {pmatrix} x_ {1} x_ {2} x_ {3} end {pmatrix}} = { begin {pmatrix} cos theta _ { 11} & cos theta _ {12} & cos theta _ {13} cos theta _ {21} & cos theta _ {22} & cos theta _ {23} cos theta _ {31} & cos theta _ {32} & cos theta _ {33} end {pmatrix}} { begin {pmatrix} x_ {1} x_ {2} х_ {3} конец {pmatrix}}}$

аналогично для

${ displaystyle mathbf {x} = { boldsymbol { mathsf {L}}} ^ {- 1} { bar { mathbf {x}}} = { boldsymbol { mathsf {L}}} ^ { mathrm {T}} { bar { mathbf {x}}}}$

Геометрическая интерпретация - это Икс_я компоненты равны сумме проецирования Икс_j компоненты на Икс_j топоры.

Цифры е_я⋅е_j организованный в матрицу, образует симметричная матрица (матрица, равная собственному транспонированию) из-за симметрии скалярных произведений, фактически это метрический тензор грамм. Напротив е_я⋅е_j или же е_я⋅е_j делать нет образуют симметричные матрицы в целом, как показано выше. Поэтому пока L матрицы по-прежнему ортогональны, они не симметричны.

За исключением вращения вокруг какой-либо одной оси, в которой Икс_я и Икс_я для некоторых я совпадают, углы не такие, как Углы Эйлера, и поэтому L матрицы не совпадают с матрицы вращения.

Преобразование точечных и перекрестных произведений (только для трех измерений)

В скалярное произведение и перекрестное произведение встречаются очень часто в приложениях векторного анализа к физике и технике, например:

• мощность переведен п объектом, оказывающим силу F со скоростью v по прямолинейному пути:

${ Displaystyle P = mathbf {v} cdot mathbf {F}}$

• касательный скорость v в какой-то момент Икс вращающегося жесткое тело с угловая скорость ω:

${ Displaystyle mathbf {v} = { boldsymbol { omega}} times mathbf {x}}$

• потенциальная энергия U из магнитный диполь из магнитный момент м в единой внешней магнитное поле B:

${ Displaystyle U = - mathbf {m} cdot mathbf {B}}$

• угловой момент J для частицы с вектор положения р и импульс п:

${ Displaystyle mathbf {J} = mathbf {r} times mathbf {p}}$

• крутящий момент τ действуя на электрический диполь из электрический дипольный момент п в единой внешней электрическое поле E:

${ displaystyle { boldsymbol { tau}} = mathbf {p} times mathbf {E}}$

• индуцированная поверхность плотность тока j_S в магнитном материале намагничивание M на поверхности с единица нормальная п:

${ Displaystyle mathbf {j} _ { mathrm {S}} = mathbf {M} times mathbf {n}}$

Как эти продукты трансформируются при ортогональных преобразованиях, показано ниже.

Точечное произведение, дельта Кронекера и метрический тензор

В скалярное произведение Каждой возможной пары базисных векторов следует из ортонормированности базиса. Для перпендикулярных пар имеем

${ displaystyle { begin {array} {cccc} mathbf {e} _ { text {x}} cdot mathbf {e} _ { text {y}} & = mathbf {e} _ { текст {y}} cdot mathbf {e} _ { text {z}} & = mathbf {e} _ { text {z}} cdot mathbf {e} _ { text {x}} mathbf {e} _ { text {y}} cdot mathbf {e} _ { text {x}} & = mathbf {e} _ { text {z}} cdot mathbf { e} _ { text {y}} & = mathbf {e} _ { text {x}} cdot mathbf {e} _ { text {z}} & = 0 end {array}}}$

а для параллельных пар мы имеем

${ displaystyle mathbf {e} _ { text {x}} cdot mathbf {e} _ { text {x}} = mathbf {e} _ { text {y}} cdot mathbf { e} _ { text {y}} = mathbf {e} _ { text {z}} cdot mathbf {e} _ { text {z}} = 1.}$

Замена декартовых меток индексным обозначением, как показано надэти результаты можно резюмировать следующим образом:

${ displaystyle mathbf {e} _ {i} cdot mathbf {e} _ {j} = delta _ {ij}}$

куда δ_ij компоненты Дельта Кронекера. Декартово основание можно использовать для представления δ таким образом.

Кроме того, каждый метрический тензор компонент грамм_ij относительно любого базиса является скалярным произведением пары базисных векторов:

${ displaystyle g_ {ij} = mathbf {e} _ {i} cdot mathbf {e} _ {j}.}$

Для декартового базиса компоненты, организованные в матрицу, следующие:

${ displaystyle mathbf {g} = { begin {pmatrix} g _ { text {xx}} & g _ { text {xy}} & g _ { text {xz}} g _ { text {yx}} & g_ { text {yy}} & g _ { text {yz}} g _ { text {zx}} & g _ { text {zy}} & g _ { text {zz}} end {pmatrix}} = { begin {pmatrix} mathbf {e} _ { text {x}} cdot mathbf {e} _ { text {x}} & mathbf {e} _ { text {x}} cdot mathbf {e} _ { text {y}} & mathbf {e} _ { text {x}} cdot mathbf {e} _ { text {z}} mathbf {e} _ { text {y}} cdot mathbf {e} _ { text {x}} & mathbf {e} _ { text {y}} cdot mathbf {e} _ { text {y} } & mathbf {e} _ { text {y}} cdot mathbf {e} _ { text {z}} mathbf {e} _ { text {z}} cdot mathbf { e} _ { text {x}} & mathbf {e} _ { text {z}} cdot mathbf {e} _ { text {y}} & mathbf {e} _ { text { z}} cdot mathbf {e} _ { text {z}} end {pmatrix}} = { begin {pmatrix} 1 & 0 & 0 0 & 1 & 0 0 & 0 & 1 end {pmatrix}}}$

таковы простейшие из возможных для метрического тензора, а именно δ:

${ displaystyle g_ {ij} = delta _ {ij}}$

Это нет верно для общих баз: ортогональные координаты имеют диагональ метрики, содержащие различные масштабные коэффициенты (т.е. не обязательно 1), а общие криволинейные координаты также может иметь ненулевые записи для недиагональных компонентов.

Скалярное произведение двух векторов а и б трансформируется в соответствии с

${ displaystyle mathbf {a} cdot mathbf {b} = { bar {a}} _ {j} { bar {b}} _ {j} = a_ {i} { mathsf {L}} _ {ij} b_ {k} ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {jk} = a_ {i} delta _ {i} {} _ {k} b_ {k } = a_ {i} b_ {i}}$

что интуитивно понятно, поскольку скалярное произведение двух векторов представляет собой единый скаляр, не зависящий от каких-либо координат. Это также применимо в более общем плане к любым системам координат, а не только к прямоугольным; скалярное произведение в одной системе координат одинаково в любой другой.

Крест и произведение, символ Леви-Чивиты и псевдовекторы

Циклические перестановки значений индекса и положительно ориентированный кубический объем.

Антициклические перестановки значений индекса и отрицательно ориентированный кубический объем.

Ненулевые значения Символ Леви-Чивита ε_ijk как объем е_я · е_j × е_k куба, натянутого на трехмерный ортонормированный базис.

Для перекрестное произведение × двух векторов результаты (почти) наоборот. Опять же, предполагая правую трехмерную декартову систему координат, циклические перестановки в перпендикулярных направлениях дают следующий вектор в циклическом наборе векторов:

${ displaystyle mathbf {e} _ { text {x}} times mathbf {e} _ { text {y}} = mathbf {e} _ { text {z}} , quad mathbf {e} _ { text {y}} times mathbf {e} _ { text {z}} = mathbf {e} _ { text {x}} , quad mathbf {e} _ { text {z}} times mathbf {e} _ { text {x}} = mathbf {e} _ { text {y}}}$

${ displaystyle mathbf {e} _ { text {y}} times mathbf {e} _ { text {x}} = - mathbf {e} _ { text {z}} , quad mathbf {e} _ { text {z}} times mathbf {e} _ { text {y}} = - mathbf {e} _ { text {x}} , quad mathbf { e} _ { text {x}} times mathbf {e} _ { text {z}} = - mathbf {e} _ { text {y}}}$

а параллельные векторы явно исчезают:

${ displaystyle mathbf {e} _ { text {x}} times mathbf {e} _ { text {x}} = mathbf {e} _ { text {y}} times mathbf { e} _ { text {y}} = mathbf {e} _ { text {z}} times mathbf {e} _ { text {z}} = { boldsymbol {0}}}$

и заменяя декартовы метки индексным обозначением как над, их можно резюмировать следующим образом:

${ displaystyle mathbf {e} _ {i} times mathbf {e} _ {j} = left [{ begin {array} {cc} + mathbf {e} _ {k} & { text {циклические перестановки:}} (i, j, k) = (1,2,3), (2,3,1), (3,1,2) - mathbf {e} _ {k} & { text {антициклические перестановки:}} (i, j, k) = (2,1,3), (3,2,1), (1,3,2) { boldsymbol {0}} & i = j end {array}} right.}$

куда я, j, k - индексы, принимающие значения 1, 2, 3. Отсюда следует, что:

${ displaystyle { mathbf {e} _ {k} cdot mathbf {e} _ {i} times mathbf {e} _ {j}} = left [{ begin {array} {cc} + 1 & { text {циклические перестановки:}} (i, j, k) = (1,2,3), (2,3,1), (3,1,2) - 1 & { text {антициклические перестановки:}} (i, j, k) = (2,1,3), (3,2,1), (1,3,2) 0 & i = j { text {или}} j = k { text {или}} k = i end {array}} right.}$

Эти перестановочные отношения и соответствующие им значения важны, и есть объект, совпадающий с этим свойством: Символ Леви-Чивита, обозначаемый ε. Записи символа Леви-Чивиты могут быть представлены декартовым основанием:

${ displaystyle varepsilon _ {ijk} = mathbf {e} _ {i} cdot mathbf {e} _ {j} times mathbf {e} _ {k}}$

что геометрически соответствует объем из куб натянутая на ортонормированные базисные векторы, со знаком, указывающим ориентация (и нет «положительный или отрицательный объем»). Здесь ориентация фиксируется ε₁₂₃ = +1, для правой системы. Система для левой руки исправит ε₁₂₃ = −1 или эквивалентно ε₃₂₁ = +1.

В скалярное тройное произведение теперь можно написать:

${ displaystyle mathbf {c} cdot mathbf {a} times mathbf {b} = c_ {i} mathbf {e} _ {i} cdot a_ {j} mathbf {e} _ {j } times b_ {k} mathbf {e} _ {k} = varepsilon _ {ijk} c_ {i} a_ {j} b_ {k}}$

с геометрической интерпретацией объема ( параллелепипед охватывает а, б, c) и алгебраически является детерминант:^[3]

${ displaystyle mathbf {c} cdot mathbf {a} times mathbf {b} = { begin {vmatrix} c _ { text {x}} & a _ { text {x}} & b _ { text { x}} c _ { text {y}} & a _ { text {y}} & b _ { text {y}} c _ { text {z}} & a _ { text {z}} & b _ { текст {z}} end {vmatrix}}}$

Это, в свою очередь, может быть использовано для перезаписи перекрестное произведение двух векторов следующим образом:

${ displaystyle { begin {array} {ll} & ( mathbf {a} times mathbf {b}) _ {i} = { mathbf {e} _ {i} cdot mathbf {a} раз mathbf {b}} = varepsilon _ { ell jk} {( mathbf {e} _ {i})} _ { ell} a_ {j} b_ {k} = varepsilon _ { ell jk } delta _ {i ell} a_ {j} b_ {k} = varepsilon _ {ijk} a_ {j} b_ {k} Rightarrow & { mathbf {a} times mathbf {b} } = ( mathbf {a} times mathbf {b}) _ {i} mathbf {e} _ {i} = varepsilon _ {ijk} a_ {j} b_ {k} mathbf {e} _ {i} end {array}}}$

В отличие от своего внешнего вида, символ Леви-Чивита не тензор, но псевдотензор, компоненты преобразуются в соответствии с:

${ displaystyle { bar { varepsilon}} _ {pqr} = det ({ boldsymbol { mathsf {L}}}) varepsilon _ {ijk} { mathsf {L}} _ {ip} { mathsf {L}} _ {jq} { mathsf {L}} _ {kr} ,.}$

Следовательно, преобразование перекрестного произведения а и б является:

${ displaystyle { begin {align} ({ bar { mathbf {a}}} times { bar { mathbf {b}}}) _ {i} & = { bar { varepsilon}} _ {ijk} { bar {a}} _ {j} { bar {b}} _ {k} & = det ({ boldsymbol { mathsf {L}}}) ; ; varepsilon _ {pqr} { mathsf {L}} _ {pi} { mathsf {L}} _ {qj} { mathsf {L}} _ {rk} ; ; a_ {m} { mathsf {L }} _ {mj} ; ; b_ {n} { mathsf {L}} _ {nk} & = det ({ boldsymbol { mathsf {L}}}) ; ; varepsilon _ {pqr} ; ; { mathsf {L}} _ {pi} ; ; { mathsf {L}} _ {qj} ({ boldsymbol { mathsf {L}}} ^ {- 1 }) _ {jm} ; ; { mathsf {L}} _ {rk} ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {kn} ; ; a_ {m } ; ; b_ {n} & = det ({ boldsymbol { mathsf {L}}}) ; ; varepsilon _ {pqr} ; ; { mathsf {L}} _ {pi} ; ; delta _ {qm} ; ; delta _ {rn} ; ; a_ {m} ; ; b_ {n} & = det ({ boldsymbol { mathsf {L}}}) ; ; { mathsf {L}} _ {pi} ; ; varepsilon _ {pqr} a_ {q} b_ {r} & = det ({ boldsymbol { mathsf {L}}}) ; ; ( mathbf {a} times mathbf {b}) _ {p} { mathsf {L}} _ {pi} end {выровнено}}}$

и так а × б трансформируется как псевдовектор, из-за определяющего фактора.

В обозначение тензорного индекса применяется к любому объекту, который имеет сущности, образующие многомерные массивы - не все с индексами по умолчанию является тензорным. Вместо этого тензоры определяются тем, как их координаты и базисные элементы изменяются при преобразовании из одной системы координат в другую.

Обратите внимание, что произведение двух векторов является псевдовектором, а произведение псевдовектора на вектор - другим вектором.

Приложения δ тензор и ε псевдотензор

Другие идентичности могут быть сформированы из δ тензор и ε псевдотензор, примечательным и очень полезным тождеством является тот, который преобразует два символа Леви-Чивиты, смежно сжатых по двум индексам, в антисимметричную комбинацию дельт Кронекера:

${ displaystyle varepsilon _ {ijk} varepsilon _ {pqk} = delta _ {ip} delta _ {jq} - delta _ {iq} delta _ {jp}}$

Формы индексов точечных и перекрестных произведений, вместе с этим тождеством, значительно облегчают манипулирование и вывод других тождества в векторном исчислении и алгебра, которые, в свою очередь, широко используются в физике и технике. Например, очевидно, что скалярное произведение и кросс-произведение являются распределительными по сравнению с векторным сложением:

${ displaystyle mathbf {a} cdot ( mathbf {b} + mathbf {c}) = a_ {i} (b_ {i} + c_ {i}) = a_ {i} b_ {i} + a_ {i} c_ {i} = mathbf {a} cdot mathbf {b} + mathbf {a} cdot mathbf {c}}$

${ displaystyle mathbf {a} times ( mathbf {b} + mathbf {c}) = mathbf {e} _ {i} varepsilon _ {ijk} a_ {j} (b_ {k} + c_ {k}) = mathbf {e} _ {i} varepsilon _ {ijk} a_ {j} b_ {k} + mathbf {e} _ {i} varepsilon _ {ijk} a_ {j} c_ { k} = mathbf {a} times mathbf {b} + mathbf {a} times mathbf {c}}$

не прибегая к каким-либо геометрическим построениям - вывод в каждом случае представляет собой быструю строку алгебры. Хотя процедура менее очевидна, можно также получить векторное тройное произведение. Переписывание в индексной записи:

${ displaystyle left [ mathbf {a} times ( mathbf {b} times mathbf {c}) right] _ {i} = varepsilon _ {ijk} a_ {j} ( varepsilon _ { k ell m} b _ { ell} c_ {m}) = ( varepsilon _ {ijk} varepsilon _ {k ell m}) a_ {j} b _ { ell} c_ {m}}$

и поскольку циклические перестановки индексов в ε символ не меняет своего значения, циклически переставляя индексы в ε_км чтобы получить ε_ℓmk позволяет нам использовать вышеуказанное δ-ε личность для преобразования ε символы в δ тензоры:

${ displaystyle { begin {align} left [ mathbf {a} times ( mathbf {b} times mathbf {c}) right] _ {i} & = ( delta _ {i ell } delta _ {jm} - delta _ {im} delta _ {j ell}) a_ {j} b _ { ell} c_ {m} & = delta _ {i ell} delta _ {jm} a_ {j} b _ { ell} c_ {m} - delta _ {im} delta _ {j ell} a_ {j} b _ { ell} c_ {m} & = a_ {j} b_ {i} c_ {j} -a_ {j} b_ {j} c_ {i} конец {выровнено}}}$

таким образом:

${ displaystyle mathbf {a} times ( mathbf {b} times mathbf {c}) = ( mathbf {a} cdot mathbf {c}) mathbf {b} - ( mathbf {a } cdot mathbf {b}) mathbf {c}}$

Обратите внимание, что это антисимметрично в б и c, как и ожидалось с левой стороны. Точно так же с помощью индексной нотации или даже просто циклической перемаркировки а, б, и c в предыдущем результате и принимая отрицательный результат:

${ displaystyle ( mathbf {a} times mathbf {b}) times mathbf {c} = ( mathbf {c} cdot mathbf {a}) mathbf {b} - ( mathbf {c } cdot mathbf {b}) mathbf {a}}$

а разница в результатах показывает, что перекрестное произведение не ассоциативно. Более сложные идентичности, например, учетверенные продукты;

${ displaystyle ( mathbf {a} times mathbf {b}) cdot ( mathbf {c} times mathbf {d}), quad ( mathbf {a} times mathbf {b}) times ( mathbf {c} times mathbf {d}), ldots}$

и так далее, можно получить аналогичным образом.

Преобразования декартовых тензоров (любое количество измерений)

Тензоры определяются как величины, которые определенным образом преобразуются при линейных преобразованиях координат.

Второго порядка

Позволять а = а_яе_я и б = б_яе_я быть двумя векторами, так что они преобразуются согласно а_j = а_яL_яj, б_j = б_яL_яj.

Тензорное произведение дает:

${ displaystyle mathbf {a} otimes mathbf {b} = a_ {i} mathbf {e} _ {i} otimes b_ {j} mathbf {e} _ {j} = a_ {i} b_ {j} mathbf {e} _ {i} otimes mathbf {e} _ {j}}$

затем применяя преобразование к компонентам

${ displaystyle { bar {a}} _ {p} { bar {b}} _ {q} = a_ {i} { mathsf {L}} _ {i} {} _ {p} b_ {j } { mathsf {L}} _ {j} {} _ {q} = { mathsf {L}} _ {i} {} _ {p} { mathsf {L}} _ {j} {} _ {q} a_ {i} b_ {j}}$

и к базам

${ displaystyle { bar { mathbf {e}}} _ {p} otimes { bar { mathbf {e}}} _ {q} = ({ boldsymbol { mathsf {L}}} ^ { -1}) _ {pi} mathbf {e} _ {i} otimes ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {qj} mathbf {e} _ {j} = ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {pi} ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {qj} mathbf {e} _ {i} otimes mathbf {e} _ {j} = { mathsf {L}} _ {ip} { mathsf {L}} _ {jq} mathbf {e} _ {i} otimes mathbf {e} _ {j}}$

дает закон преобразования тензора второго порядка. Тензор а⊗б инвариантно относительно этого преобразования:

${ displaystyle { begin {array} {cl} { bar {a}} _ {p} { bar {b}} _ {q} { bar { mathbf {e}}} _ {p} otimes { bar { mathbf {e}}} _ {q} & = { mathsf {L}} _ {kp} { mathsf {L}} _ { ell q} a_ {k} b _ { ell } , ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {pi} ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {qj} mathbf { e} _ {i} otimes mathbf {e} _ {j} & = { mathsf {L}} _ {kp} ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {pi} { mathsf {L}} _ { ell q} ({ boldsymbol { mathsf {L}}} ^ {- 1}) _ {qj} , a_ {k} b _ { ell} mathbf {e} _ {i} otimes mathbf {e} _ {j} & = delta _ {k} {} _ {i} delta _ { ell j} , a_ {k} b _ { ell} mathbf {e} _ {i} otimes mathbf {e} _ {j} & = a_ {i} b_ {j} mathbf {e} _ {i} otimes mathbf {e} _ {j} end {array}}}$