WikiDer > Пятиугольный шестигранник - Википедия
| Пятиугольный шестиугольник | |
|---|---|
 (Нажмите здесь, чтобы повернуть модель) | |
| Тип | Каталонский твердый |
| Диаграмма Кокстера | |
| Обозначение Конвея | gD |
| Тип лица | V3.3.3.3.5 нерегулярный пятиугольник |
| Лица | 60 |
| Края | 150 |
| Вершины | 92 |
| Вершины по типу | 12 {5} 20+60 {3} |
| Группа симметрии | я, 1/2ЧАС3, [5,3]+, (532) |
| Группа вращения | Я, [5,3]+, (532) |
| Двугранный угол | 153°10′43″ |
| Характеристики | выпуклый, лицо переходный хиральный |
 Курносый додекаэдр (двойственный многогранник) |  Сеть |
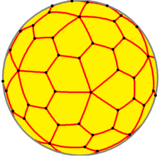
В геометрия, а пятиугольный гексеконтаэдр это Каталонский твердый, двойной курносый додекаэдр. Он имеет две различные формы: зеркальные изображения (или же "энантиоморфы") друг друга. У него 92 вершины, которые охватывают 60 пятиугольных граней. Это каталонское твердое тело с наибольшим числом вершин. Среди каталонских и Архимедов твердых тел, он имеет второе по величине число вершин после усеченный икосододекаэдр, имеющий 120 вершин.
Строительство
Пятиугольный гексеконтаэдр можно построить из курносого додекаэдра, не взяв двойника. Пятиугольные пирамиды добавляются к 12 пятиугольным граням курносого додекаэдра, а треугольные пирамиды добавляются к 20 треугольным граням, которые не имеют общего ребра с пятиугольником. Высота пирамиды регулируется, чтобы сделать их копланарными с другими 60 треугольными гранями курносого додекаэдра. В результате получился пятиугольный гексеконтаэдр.[1]
Геометрия
Лица неправильные пятиугольники с двумя длинными краями и тремя короткими краями. Позволять - действительный нуль многочлена , куда это Золотое сечение.Тогда соотношение длины кромки определяется как:
- .
Грани имеют четыре равных тупых угла и один острый угол (между двумя длинными краями). Тупые углы равны , а острый равен . Двугранный угол равен Обратите внимание, что центры граней курносый додекаэдр не могут служить непосредственно вершинами пятиугольного гексаконтаэдра: четыре центра треугольника лежат в одной плоскости, а центр пятиугольника - нет; его нужно вытолкнуть радиально, чтобы сделать его копланарным с центрами треугольников. Следовательно, не все вершины пятиугольного гексаконтаэдра лежат на одной сфере, и по определению он не является сферой. зоноэдр.
Чтобы найти объем и площадь поверхности пятиугольного гексеконтаэдра, обозначьте более длинную сторону одной из пятиугольных граней как , и установить константу т[2] .
Тогда площадь поверхности (A) равна:
.
А объем (V) равен:
.
Вариации
Изоэдральный варианты могут быть выполнены с пятиугольными гранями с 3 длинами кромок.
Этот показанный вариант можно построить, добавив пирамиды к 12 пятиугольным граням и 20 треугольным граням курносый додекаэдр таким образом, что новые треугольные грани параллельны другим треугольникам и могут быть объединены с гранями пятиугольника.
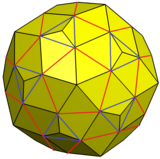 Курносый додекаэдр с увеличенными пирамидами и объединенными гранями |  Пример вариации | 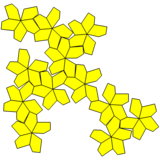 Сеть |
Ортогональные проекции
В пятиугольный гексеконтаэдр имеет три положения симметрии, две по вершинам и одну по середине.
| Проективный симметрия | [3] | [5]+ | [2] |
|---|---|---|---|
| Изображение |  |  |  |
| Двойной изображение |  |  |  |
Связанные многогранники и мозаики
| Семейство однородных икосаэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия: [5,3], (*532) | [5,3]+, (532) | ||||||
 |  |  |  |  |  |  |  |
| {5,3} | т {5,3} | г {5,3} | т {3,5} | {3,5} | рр {5,3} | tr {5,3} | ср {5,3} |
| Двойники к однородным многогранникам | |||||||
 |  |  |  |  | |||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
Этот многогранник топологически связан как часть последовательности многогранников и мозаик пятиугольников с конфигурации лица (V3.3.3.3.п). (Последовательность переходит в разбиение гиперболической плоскости на любую п.) Эти лицо переходный фигуры имеют (n32) вращательные симметрия.
| п32 мутации симметрии курносых плиток: 3.3.3.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия п32 | Сферический | Евклидово | Компактный гиперболический | Paracomp. | ||||
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| Курносый цифры |  |  |  |  |  |  |  |  |
| Конфиг. | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| Гироскоп цифры |  |  |  |  |  |  |  |  |
| Конфиг. | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3.3.3.3.8 | V3.3.3.3.∞ |
Смотрите также
Рекомендации
- ^ Ссылка
- ^ "Пятиугольный гексеконтаэдр - Калькулятор геометрии". rechneronline.de. Получено 2020-05-26.
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X. (Раздел 3-9)
- Веннингер, Магнус (1983), Двойные модели, Издательство Кембриджского университета, Дои:10.1017 / CBO9780511569371, ISBN 978-0-521-54325-5, МИСТЕР 0730208 (Тринадцать полуправильных выпуклых многогранников и их двойники, Пентагональный гексеконтаэдр)
- Симметрии вещей 2008, Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штраус, ISBN 978-1-56881-220-5 [1] (Глава 21, Именование архимедовых и каталонских многогранников и мозаик, стр. 287, пятиугольный гексеконтаэдр)
внешняя ссылка
- Эрик В. Вайсштейн, Пятиугольный шестиугольник (Каталонский твердый) в MathWorld.
- Пятиугольный гексеконтраэдр - Интерактивная модель многогранника
| Этот многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |











![{ displaystyle t = { frac {{ sqrt [{3}] {44 + 12 phi (9 + { sqrt {81 phi -15}})}} + { sqrt [{3}] { 44 + 12 phi (9 - { sqrt {81 phi -15}})}} - 4} {12}} приблизительно 0,471 , 575 , 629 , 622}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02d9b5af0885722dd1aa9b9332cf828d9755aedf)