WikiDer > Уменьшенный трапецоэдр
| Набор уменьшенных трапецоэдров | |
|---|---|
 Пример квадратной формы | |
| Лица | п воздушные змеи п треугольники 1 н-угольник |
| Края | 4n |
| Вершины | 2n + 1 |
| Группа симметрии | CNV, [n], (* nn) |
| Группа вращения | Cп, [n]+, (nn) |
| Двойной многогранник | самодвойственный |
| Характеристики | выпуклый |
В геометрия, а уменьшенный трапецоэдр это многогранник в бесконечном множестве многогранников, построенных удалением одной из полярных вершин трапецоэдр и заменив его новым лицом (уменьшение). Имеет одну правильную n-угольную базовую грань, п треугольники лица вокруг основания, и п воздушные змеи встреча наверху. Воздушных змеев также можно заменить ромбами с определенными пропорциями.
Наряду с набором пирамиды и удлиненные пирамиды, эти фигуры топологически самодвойственный.
Его также можно рассматривать как усиленную н-угольную антипризму с н-угольным пирамида добавлен к одному из п-угольные грани, высота которых регулируется таким образом, чтобы верхние грани треугольника с антипризмой могли быть параллельны граням пирамиды и объединены в грани в форме змея.
Они также связаны с гиродлинные пирамиды, как усиленные антипризмы и которые являются твердыми телами Джонсона для п = 4 и 5. В этой последовательности есть наборы из двух треугольников вместо граней змея.
Примеры
| Симметрия | C3в | C4в | C5в | C6v | C7v | C8v ... | |
|---|---|---|---|---|---|---|---|
| Изображение |  |  |  |  |  | ||
| Ромбический форма |  |  |  |  |  |  | |
| Сеть |  |  |  |  |  |  | |
| Лица | 3 трапеции 3 + 1 треугольник | 4 трапеции 4 треугольника 1 квадрат | 5 трапеций 5 треугольников 1 пятиугольник | 6 трапеций 6 треугольников 1 шестиугольник | 7 трапеций 7 треугольников 1 семиугольник | 8 трапеций 7 треугольников 1 восьмиугольник | |
| Края | 12 | 16 | 20 | 24 | 28 | 32 | |
| Вершины | 7 | 9 | 11 | 13 | 15 | 17 | |
| Трапецоэдры | |||||||
| Симметрия | D3D | D4d | D5d | D6d | D7d | D8d | |
| Изображение |  3 | 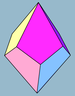 4 | 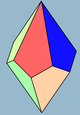 5 | 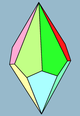 6 | |||
| Лица | 3 + 3 ромби (Или квадраты) | 4 + 4 воздушных змея | 5 + 5 воздушных змеев | 6 + 6 воздушных змеев | 7 + 7 воздушных змеев | ||
| Края | 12 | 16 | 20 | 24 | 28 | ||
| Вершины | 8 | 10 | 12 | 14 | 16 | ||
| Гиро-удлиненная пирамида или (усиленные антипризмы) | |||||||
| Симметрия | C3в | C4в | C5в | C6v | C7v | C8v | |
| Изображение |  3 |  4 |  5 | 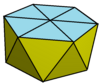 6 | |||
| Лица | 9 + 1 треугольников | 12 треугольников 1 квадратик | 15 треугольников 1 пятиугольник | 18 треугольников 1 шестиугольник | |||
Особые случаи
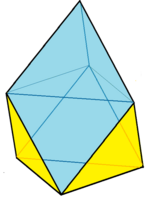
Есть три особых случая геометрии уменьшенный треугольный трапецоэдр. Самый простой - это уменьшенный куб. В Chestahedron, названный в честь художника Фрэнка Честера, построен из равносторонних треугольников вокруг основания, а геометрия настроена так, чтобы грани воздушных змеев имели ту же площадь, что и равносторонние треугольники.[1][2] Последнее можно увидеть по увеличение обычный тетраэдр и октаэдр, оставляя 10 равносторонних треугольных граней, а затем объединяя 3 набора параллельных равносторонних треугольных граней в 3 (60 градусов) ромбических граней. Его также можно рассматривать как тетраэдр с 3 из 4 вершин. исправленный. Три ромбических грани складываются плоско, образуя половину гексаграмма.
| Гептаэдр топология # 31 Уменьшено куб | Chestahedron (Лица одинаковой площади) | Расширенный октаэдр (Равносторонние лица) |
|---|---|---|
 |  | |
 | 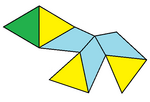 |  |
| 3 квадраты 3 45-45-90 треугольников 1 равносторонний треугольник лицо | 3 кайта 3 + 1 равносторонние треугольные грани | 3 ромбические грани 60 градусов 3 + 1 равносторонние треугольные грани |
Смотрите также
- Удлиненная пирамида
- Гиро-удлиненная бипирамида
- Удлиненная бипирамида
- Гиро-удлиненная пирамида
- Тетраэдрически уменьшенный додекаэдр
Рекомендации
- ^ "Геометрия каштаэдра". Искусство и наука Фрэнка Честера. Получено 2020-01-22.
- ^ Донке, Ханс-Йоаким (март 2011 г.). «Превращение тетраэдра в четырехгранник». вольфрам Альфа. Получено 22 января 2020.