WikiDer > Дискриминант поля алгебраических чисел

Фундаментальная область кольца целых поля K получен из Q путем присоединения к корню Икс³ − Икс² − 2Икс + 1. Эта фундаментальная область находится внутри K ⊗_Qр. Дискриминант K это 49 = 7². Соответственно, объем фундаментальной области равен 7 и K только разветвленный в 7.

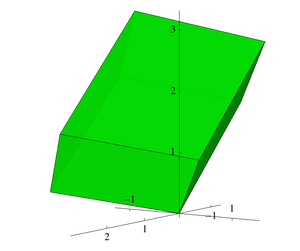
В математика, то дискриминант из поле алгебраических чисел числовой инвариантный что, грубо говоря, измеряет размер (кольцо целых чисел поля алгебраических чисел. В частности, он пропорционален квадрату объема фундаментальная область кольца целых чисел, и он регулирует, какие простые числа находятся разветвленный.

Дискриминант является одним из самых основных инвариантов числового поля и встречается в нескольких важных аналитический формулы, такие как функциональное уравнение из Дзета-функция Дедекинда из K, а формула аналитического числа классов за K. Теорема из Эрмит утверждает, что существует только конечное число числовых полей ограниченного дискриминанта, однако определение этой величины по-прежнему открытая проблема, и предмет текущего исследования.^[1]

Дискриминант K можно назвать абсолютный дискриминант из K отличить его от относительный дискриминант из расширение K/L числовых полей. Последний является идеальный в кольце целых чисел L, и, как и абсолютный дискриминант, указывает, какие простые числа разветвляются в K/L. Это обобщение абсолютного дискриминанта с учетом L быть больше, чем Q; на самом деле, когда L = Q, относительный дискриминант K/Q это главный идеал из Z порожденный абсолютным дискриминантом K.

Определение

Позволять K - поле алгебраических чисел, и пусть О_K быть его кольцо целых чисел. Позволять б₁, ..., б_п быть целостная основа из О_K (т.е. основа как Z-модуль), и пусть {σ₁, ..., σ_п} - множество вложений K в сложные числа (т.е. инъективный гомоморфизмы колец K → C). В дискриминант из K это квадрат из детерминант из п к п матрица B чей (я,j) -запись σ_я(б_j). Символично,

${ displaystyle Delta _ {K} = det left ({ begin {array} {cccc} sigma _ {1} (b_ {1}) & sigma _ {1} (b_ {2}) & cdots & sigma _ {1} (b_ {n}) sigma _ {2} (b_ {1}) & ddots && vdots vdots && ddots & vdots sigma _ {n} (b_ {1}) & cdots & cdots & sigma _ {n} (b_ {n}) end {array}} right) ^ {2}.}$

Эквивалентно след из K к Q может быть использован. В частности, определите форма следа быть матрицей, (я,j) -записьТр_K/Q(б_яб_j). Эта матрица равна B^ТB, поэтому дискриминант K - определитель этой матрицы.

Примеры

• Поля квадратичных чисел: позволять d быть целое число без квадратов, то дискриминант ${ Displaystyle К = mathbf {Q} ({ sqrt {d}})}$ является^[2]

${ displaystyle Delta _ {K} = left {{ begin {array} {ll} d & { text {if}} d Equiv 1 { pmod {4}} 4d & { text {if }} d Equiv 2,3 { pmod {4}}. end {array}} right.}$

Целое число, которое встречается как дискриминант поля квадратичных чисел, называется основной дискриминант.^[3]

• Циклотомические поля: позволять п > 2 - целое число, пусть ζ_п быть примитивный пй корень единства, и разреши K_п = Q(ζ_п) быть п-го круговое поле. Дискриминант K_п дан кем-то^[2][4]

${ displaystyle Delta _ {K_ {n}} = (- 1) ^ { varphi (n) / 2} { frac {n ^ { varphi (n)}} { displaystyle prod _ {p | n} p ^ { varphi (n) / (p-1)}}}}$

куда ${ Displaystyle varphi (п)}$ является Функция Эйлера, а произведение в знаменателе больше простых чисел п разделение п.

• Степенные основания: в случае, когда кольцо целых чисел имеет интегральная основа мощности, то есть может быть записано как О_K = Z[α] дискриминант K равно дискриминант из минимальный многочлен из α. Чтобы убедиться в этом, можно выбрать интегральный базис О_K быть б₁ = 1, б₂ = α, б₃ = α², ..., б_п = α^п−1. Тогда матрица в определении - это Матрица Вандермонда связанный с α_я = σ_я(α), квадрат определителя которого равен

${ Displaystyle prod _ {1 Leq я$

что и есть определение дискриминанта минимального многочлена.

• Позволять K = Q(α) - числовое поле, полученное прилегающий а корень α из многочлен Икс³ − Икс² − 2Икс - 8. Это Ричард ДедекиндОригинальный пример числового поля, кольцо целых чисел которого не имеет степенного базиса. Целочисленный базис задается {1, α, α (α + 1) / 2} и дискриминантом K равно -503.^[5][6]
• Повторяющиеся дискриминанты: дискриминант квадратичного поля однозначно идентифицирует его, но это, в общем, неверно для уровнем выше числовые поля. Например, есть два неизоморфный кубические поля дискриминанта 3969. Они получаются присоединением корня многочлена Икс³ − 21Икс + 28 или же Икс³ − 21Икс − 35, соответственно.^[7]

Основные результаты

• Теорема Брилла:^[8] В знак дискриминанта равна (−1)^р₂ куда р₂ это количество сложные места из K.^[9]
• Премьер п разветвляется в K если и только если п делит Δ_K .^[10]
• Теорема Штикельбергера:^[11]

${ displaystyle Delta _ {K} Equiv 0 { text {или}} 1 { pmod {4}}.}$

• Связь Минковского:^[12] Позволять п обозначить степень расширения K/Q и р₂ количество сложных мест K, тогда

${ displaystyle | Delta _ {K} | ^ {1/2} geq { frac {n ^ {n}} {n!}} left ({ frac { pi} {4}} right ) ^ {r_ {2}} geq { frac {n ^ {n}} {n!}} left ({ frac { pi} {4}} right) ^ {n / 2}.}$

• Теорема Минковского:^[13] Если K не является Q, то | Δ_K| > 1 (это непосредственно следует из оценки Минковского).
• Теорема Эрмита – Минковского:^[14] Позволять N быть положительным целым числом. Имеется лишь конечное число (с точностью до изоморфизмов) полей алгебраических чисел K с | Δ_K| < N. Опять же, это следует из оценки Минковского вместе с теоремой Эрмита (что существует только конечное число полей алгебраических чисел с заданным дискриминантом).

История

Ричард Дедекинд показал, что каждое числовое поле обладает целостной базой, что позволило ему определить дискриминант произвольного числового поля.^[15]

Определение дискриминанта общего поля алгебраических чисел, K, был подарен Дедекиндом в 1871 году.^[15] К этому моменту он уже знал взаимосвязь между дискриминантом и ветвлением.^[16]

Теорема Эрмита предшествовала общему определению дискриминанта, которое Чарльз Эрмит опубликовал в 1857 году.^[17] В 1877 г. Александр фон Бриль определили знак дискриминанта.^[18] Леопольд Кронекер впервые сформулировал теорему Минковского в 1882 году,^[19] хотя первое доказательство было дано Германом Минковским в 1891 году.^[20] В том же году Минковский опубликовал оценку дискриминанта.^[21] Ближе к концу девятнадцатого века, Людвиг Штикельбергер получил свою теорему о вычете дискриминанта по модулю четыре.^[22][23]

Относительный дискриминант

Дискриминант, определенный выше, иногда называют абсолютный дискриминант K отличить его от относительный дискриминант Δ_K/L расширения числовых полей K/L, что является идеалом в О_L. Относительный дискриминант определяется аналогично абсолютному дискриминанту, но должен учитывать, что идеалы в О_L не может быть принципиальным и что не может быть О_L базис О_K. Пусть {σ₁, ..., σ_п} - множество вложений K в C которые идентичны на L. Если б₁, ..., б_п есть какая-то основа K над L, позволять d(б₁, ..., б_п) - квадрат определителя п к п матрица, чья (я,j) -запись σ_я(б_j). Тогда относительный дискриминант K/L идеал, порожденный d(б₁, ..., б_п) в качестве {б₁, ..., б_п} изменяется по всем целым базам K/L. (т.е. базы со свойством, что б_я ∈ О_K для всех я.) В качестве альтернативы относительный дискриминант K/L это норма из разные из K/L.^[24] Когда L = Q, относительный дискриминант Δ_K/Q главный идеал Z порожденная абсолютным дискриминантом Δ_K . В башня полей K/L/F относительные дискриминанты связаны соотношением

${ displaystyle Delta _ {K / F} = { mathcal {N}} _ {L / F} left ({ Delta _ {K / L}} right) Delta _ {L / F} ^ {[K: L]}}$

куда ${ Displaystyle { mathcal {N}}}$ обозначает относительный норма.^[25]

Разветвление

Относительный дискриминант регулирует разветвление данные расширения поля K/L. Главный идеал п из L разветвляется в K тогда и только тогда, когда он делит относительный дискриминант Δ_K/L. Расширение является неразветвленным тогда и только тогда, когда дискриминант является единичным идеалом.^[24] Приведенная выше оценка Минковского показывает, что не существует нетривиальных неразветвленных расширений Q. Поля больше чем Q могут иметь неразветвленные расширения: например, для любого поля с номер класса больше единицы, это Поле классов Гильберта является нетривиальным неразветвленным расширением.

Корневой дискриминант

В корневой дискриминант числового поля, Kстепени п, часто обозначаемый rd_K, определяется как п-корень -й степени абсолютного значения (абсолютного) дискриминанта K.^[26] Связь между относительными дискриминантами в башне полей показывает, что корневой дискриминант не изменяется в неразветвленном расширении. Существование полевая башня класса дает ограничения на корневой дискриминант: существование бесконечной башни поля классов над Q(√-м) куда м = 3 · 5 · 7 · 11 · 19 показывает, что существует бесконечно много полей с корневым дискриминантом 2√м ≈ 296.276.^[27] Если мы позволим р и 2s - количество действительных и сложных вложений, так что п = р + 2s, положить ρ = р/п и σ = 2s/п. Набор α(ρ, σ) быть точной нижней гранью rd_K за K с (г ', 2s ') = (ρn, σn). У нас есть (для всех достаточно больших n) ^[27]

${ Displaystyle альфа ( rho, sigma) geq 60,8 ^ { rho} 22,3 ^ { sigma}}$

и исходя из предположения обобщенная гипотеза Римана

${ Displaystyle альфа ( rho, sigma) geq 215.3 ^ { rho} 44.7 ^ { sigma}.}$

Итак, у нас есть α(0,1) <296,276. Мартине показал α(0,1) <93 и α(1,0) < 1059.^[27][28] Войт 2008 доказывает, что для полностью реальных полей корневой дискриминант> 14, за 1229 исключениями.

Отношение к другим величинам

• Когда встроен в ${ Displaystyle K otimes _ { mathbf {Q}} mathbf {R}}$, объем фундаментальной области О_K является ${ displaystyle { sqrt {| Delta _ {K} |}}}$ (иногда другой мера используется и полученный объем ${ displaystyle 2 ^ {- r_ {2}} { sqrt {| Delta _ {K} |}}}$, куда р₂ количество сложных мест K).
• Благодаря появлению в этом томе дискриминант также входит в функциональное уравнение дзета-функции Дедекинда K, а значит, и в формуле аналитического числа классов, а Теорема Брауэра – Зигеля.
• Относительный дискриминант K/L это Артин дирижер из регулярное представительство из Группа Галуа из K/L. Это обеспечивает связь с дирижерами Артина символы группы Галуа K/L, называется формула проводник-дискриминант.^[29]

Примечания

Рекомендации

Основные источники

• Бриль, Александр фон (1877), "Ueber die Discriminante", Mathematische Annalen, 12 (1): 87–89, Дои:10.1007 / BF01442468, JFM 09.0059.02, МИСТЕР 1509928, получено 2009-08-22
• Дедекинд, Ричард (1871), Vorlesungen über Zahlentheorie von P.G. Лежен Дирихле (2-е изд.), Vieweg, получено 2009-08-05
• Дедекинд, Ричард (1878), "Uber den Zusammenhang zwischen der Theorie der Ideale und der Theorie der höheren Congruenzen", Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 23 (1), получено 2009-08-20
• Эрмит, Чарльз (1857), "Extrait d'une lettre de M. C. Hermite à M. Borchardt sur le nombre limité d'irrationalités auxquelles se réduisent les racines des équations à coefficients entiers entiers complex d'un degré et d'un discinant donnés", Журнал Крелля, 1857 (53): 182–192, Дои:10.1515 / crll.1857.53.182, получено 2009-08-20
• Кронекер, Леопольд (1882), "Grundzüge einer arithmetischen Theorie der algebraischen Grössen", Журнал Крелля, 92: 1–122, JFM 14.0038.02, получено 2009-08-20
• Минковский, Германн (1891a), "Ueber die positiven quadratischen Formen und über kettenbruchähnliche Algorithmen", Журнал Крелля, 1891 (107): 278–297, Дои:10.1515 / crll.1891.107.278, JFM 23.0212.01, получено 2009-08-20
• Минковский, Германн (1891b), "Теории арифметики", Comptes rendus de l'Académie des Sciences, 112: 209–212, JFM 23.0214.01
• Стикельбергер, Людвиг (1897), "Über eine neue Eigenschaft der Diskriminanten algebraischer Zahlkörper", Труды Первого Международного конгресса математиков, Цюрих, стр. 182–193, JFM 29.0172.03

Вторичные источники

• Бурбаки, Николас (1994). Элементы истории математики. Перевод Мелдрам, Джон. Берлин: Springer-Verlag. ISBN 978-3-540-64767-6. МИСТЕР 1290116.
• Коэн, Анри (1993), Курс вычислительной алгебраической теории чисел, Тексты для выпускников по математике, 138, Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-3-540-55640-4, МИСТЕР 1228206
• Коэн, Анри; Диас-и-Диас, Франсиско; Оливье, Мишель (2002), «Обзор дискриминантного подсчета», в Фикере, Клаус; Коэль, Дэвид Р. (ред.), Алгоритмическая теория чисел, Труды, 5-й Международный симпозиум, ANTS-V, Сиднейский университет, июль 2002 г., Конспект лекций по информатике, 2369, Берлин: Springer-Verlag, стр. 80–94, Дои:10.1007/3-540-45455-1_7, ISBN 978-3-540-43863-2, ISSN 0302-9743, МИСТЕР 2041075
• Фрёлих, Альбрехт; Тейлор, Мартин (1993), Алгебраическая теория чисел, Кембриджские исследования по высшей математике, 27, Издательство Кембриджского университета, ISBN 978-0-521-43834-6, МИСТЕР 1215934
• Кох, Гельмут (1997), Алгебраическая теория чисел, Энцикл. Математика. Наук, 62 (2-е издание 1-го изд.), Springer-Verlag, ISBN 3-540-63003-1, Zbl 0819.11044
• Наркевич, Владислав (2004), Элементарная и аналитическая теория алгебраических чисел, Springer Monographs in Mathematics (3-е изд.), Берлин: Springer-Verlag, ISBN 978-3-540-21902-6, МИСТЕР 2078267
• Нойкирх, Юрген (1999). Алгебраическая теория чисел. Grundlehren der Mathematischen Wissenschaften. 322. Берлин: Springer-Verlag. ISBN 978-3-540-65399-8. МИСТЕР 1697859. Zbl 0956.11021.
• Серр, Жан-Пьер (1967), "Локальная теория поля классов", в Касселс, Дж. У. С.; Фрёлих, Альбрехт (ред.), Алгебраическая теория чисел, Труды учебной конференции в Университете Сассекса, Брайтон, 1965 г., Лондон: Academic Press, ISBN 0-12-163251-2, МИСТЕР 0220701
• Войт, Джон (2008), "Перечисление полей полностью действительных чисел ограниченного корневого дискриминанта", в ван дер Поортен, Альфред Дж.; Стейн, Андреас (ред.), Алгоритмическая теория чисел. Протоколы 8-го Международного симпозиума, ANTS-VIII, Банф, Канада, май 2008 г., Конспект лекций по информатике, 5011, Берлин: Springer-Verlag, стр. 268–281, arXiv:0802.0194, Дои:10.1007/978-3-540-79456-1_18, ISBN 978-3-540-79455-4, МИСТЕР 2467853, Zbl 1205.11125
• Вашингтон, Лоуренс (1997), Введение в циклотомические поля, Тексты для выпускников по математике, 83 (2-е изд.), Берлин, Нью-Йорк: Springer-Verlag, ISBN 978-0-387-94762-4, МИСТЕР 1421575, Zbl 0966.11047

дальнейшее чтение

• Милн, Джеймс С. (1998), Алгебраическая теория чисел, получено 2008-08-20