WikiDer > Додекагональный трапецииэдр
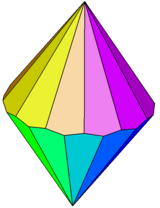
| Додекагональный трапецииэдр | |
|---|---|
 | |
| Тип | трапецоэдр |
| Конвей | dA12 |
| Диаграмма Кокстера | |
| Лица | 24 воздушные змеи |
| Края | 48 |
| Вершины | 26 |
| Конфигурация лица | V12.3.3.3 |
| Группа симметрии | D12d, [2+, 24], (2 * 12), порядок 48 |
| Группа вращения | D12, [2,12]+, (2.2.12), порядок 24 |
| Двойной многогранник | Додекагональная антипризма |
| Характеристики | выпуклый, лицо переходный |
В двенадцатигранный трапецоэдр или же дельтоэдр входит в бесконечную серию граней однородных (равногранный) многогранники, которые двойственный многогранник к антипризмы. Он имеет 24 лица, которые конгруэнтный воздушные змеи.
Смотрите также
| Семья п-гональный трапецоэдры | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Изображение многогранника |  |  |  |  |  |  |  |  | ... | Апейрогональный трапецоэдр | |
| Сферическое мозаичное изображение |  |  |  |  |  |  |  |  | Плоское мозаичное изображение | ||
| Конфигурация лица Vп.3.3.3 | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | V10.3.3.3 | V12.3.3.3 | ... | V∞.3.3.3 |
внешняя ссылка
- Вайсштейн, Эрик В. «Трапецоэдр». MathWorld.
- Многогранники виртуальной реальности www.georgehart.com: Энциклопедия многогранников
- Обозначение Конвея для многогранников Попробуйте: «A12»
| Этот многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |