WikiDer > Усеченная апейрогональная мозаика порядка 3

Усеченная апейрогональная мозаика порядка 3
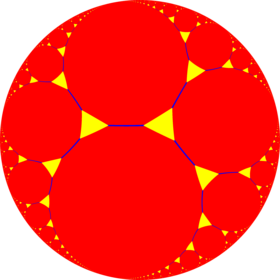Модель диска Пуанкаре из гиперболическая плоскость
Тип	Гиперболическая равномерная мозаика
Конфигурация вершины	3.∞.∞
Символ Шлефли	т {∞, 3}
Символ Wythoff	2 3 | ∞
Диаграмма Кокстера
Группа симметрии	[∞,3], (*∞32)
Двойной	Треугольная мозаика триакиса бесконечного порядка
Характеристики	Вершинно-транзитивный

В геометрия, то усеченная апейрогональная мозаика порядка 3 это равномерная черепица из гиперболическая плоскость с Символ Шлефли из t {∞, 3}.

Двойная черепица

Двойная черепица, треугольная мозаика Триаки бесконечного порядка, имеет конфигурация лица V3.∞.∞.

Связанные многогранники и мозаика

Это гиперболическое разбиение топологически связано как часть последовательности равномерных усеченный многогранники с конфигурации вершин (3.2n.2n) и [n, 3] Группа Кокстера симметрия.

*п32 мутации симметрии усеченных мозаик: t {п,3} [ v т е ]
Симметрия *п32 [n, 3]	Сферический				Евклид.	Компактная гиперболия.		Paraco.	Некомпактный гиперболический
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i, 3]	[9i, 3]	[6i, 3]
Усеченный цифры
Символ	т {2,3}	т {3,3}	т {4,3}	т {5,3}	т {6,3}	т {7,3}	т {8,3}	т {∞, 3}	т {12i, 3}	т {9i, 3}	т {6i, 3}
Triakis цифры
Конфиг.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.∞.∞

Паракомпактные равномерные мозаики в семействе [∞, 3] [ v т е ]
Симметрия: [∞,3], (*∞32)							[∞,3]+ (∞32)	[1+,∞,3] (*∞33)		[∞,3+] (3*∞)
		=	=	=				= или же	= или же	=
{∞,3}	т {∞, 3}	г {∞, 3}	т {3, ∞}	{3,∞}	rr {∞, 3}	tr {∞, 3}	sr {∞, 3}	h {∞, 3}	час2{∞,3}	s {3, ∞}
Униформа двойников
V∞3	V3.∞.∞	V (3.∞)2	V6.6.∞	V3∞	V4.3.4.∞	V4.6.∞	V3.3.3.3.∞	V (3.∞)3		V3.3.3.3.3.∞

Смотрите также

Викискладе есть медиафайлы по теме Равномерная мозаика 3-i-i.

• Список однородных плоских мозаик
• Замощения правильных многоугольников
• Равномерные мозаики в гиперболической плоскости

Рекомендации