WikiDer > Метод конечных элементов
| Дифференциальные уравнения | |||||
|---|---|---|---|---|---|
 Дифференциальные уравнения Навье – Стокса. используется для имитации воздушного потока вокруг препятствия. | |||||
| Классификация | |||||
Типы
| |||||
Отношение к процессам | |||||
| Решение | |||||
Существование и уникальность | |||||
Методы решения | |||||
В метод конечных элементов (МКЭ) - наиболее распространенный метод решения инженерных и математические модели. Типичные проблемные области, представляющие интерес, включают традиционные области структурный анализ, теплопередача, поток жидкости, общественный транспорт и электромагнитный потенциал. МКЭ - это особый численный метод для решения уравнения в частных производных в двух или трех пространственных переменных (т. е. некоторые краевые задачи). Чтобы решить проблему, FEM подразделяет большую систему на более мелкие и простые части, которые называются конечные элементы. Это достигается за счет определенного пространства дискретизация в габаритах пространства, что реализуется за счет строительства сетка объекта: числовая область решения, имеющая конечное число точек. Постановка краевой задачи методом конечных элементов в конечном итоге приводит к системе алгебраические уравнения. Метод аппроксимирует неизвестную функцию по области.[1]Простые уравнения, моделирующие эти конечные элементы, затем собираются в более крупную систему уравнений, которая моделирует всю проблему. Затем FEM использует вариационные методы от вариационное исчисление для аппроксимации решения путем минимизации связанной функции ошибок.
Учеба или анализируя явление с МКЭ часто называют анализ методом конечных элементов (FEA).
Базовые концепты
Разделение всего домена на более простые части имеет ряд преимуществ:[2]
- Точное отображение сложной геометрии
- Включение разнородных свойств материала
- Легкое представление общего решения
- Захват локальных эффектов.
Типичная работа метода включает (1) разделение области задачи на набор подобластей, каждая подобласть представлена набором элементных уравнений исходной задачи, с последующим (2) систематическим повторным объединением всех наборов элементных уравнений в глобальная система уравнений для окончательного расчета. Глобальная система уравнений имеет известные методы решения и может быть вычислена из начальные значения исходной задачи, чтобы получить числовой ответ.
На первом шаге, описанном выше, элементные уравнения представляют собой простые уравнения, которые локально аппроксимируют исходные комплексные уравнения, подлежащие изучению, где исходные уравнения часто уравнения в частных производных (PDE). Чтобы объяснить приближение в этом процессе, метод конечных элементов обычно вводится как частный случай Метод Галеркина. На математическом языке этот процесс состоит в построении интеграла от внутренний продукт остатка и весовые функции и установите интеграл равным нулю. Проще говоря, это процедура, которая сводит к минимуму ошибку аппроксимации путем подгонки пробных функций в УЧП. Невязка - это ошибка, вызванная пробными функциями, а весовые функции многочлен аппроксимационные функции, проецирующие невязку. Процесс исключает все пространственные производные из PDE, таким образом аппроксимируя PDE локально с помощью
- набор алгебраические уравнения за устойчивое состояние проблемы,
- набор обыкновенные дифференциальные уравнения за преходящий проблемы.
Эти наборы уравнений являются уравнениями элементов. Они есть линейный если лежащий в основе PDE линейный, и наоборот. Системы алгебраических уравнений, возникающие в стационарных задачах, решаются с использованием числовая линейная алгебра методы, а обыкновенное дифференциальное уравнение наборы, которые возникают в переходных задачах, решаются численным интегрированием с использованием стандартных методов, таких как Метод Эйлера или Рунге-Кутта метод.
На шаге (2) выше глобальная система уравнений генерируется из уравнений элементов посредством преобразования координат из локальных узлов подобластей в глобальные узлы домена. Это пространственное преобразование включает соответствующие регулировка ориентации применительно к ссылке система координат. Процесс часто выполняется программным обеспечением FEM с использованием координировать данные, полученные из поддоменов.
FEM лучше всего понять из его практического применения, известного как конечно-элементный анализ (FEA). FEA применительно к инженерное дело вычислительный инструмент для выполнения инженерный анализ. Он включает использование создание сетки методы разделения сложная проблема на мелкие элементы, а также использование программного обеспечения программа закодирована с алгоритмом FEM. При применении FEA сложная проблема обычно связана с физической системой с лежащей в основе физика такой как Уравнение Эйлера-Бернулли для пучка, то уравнение теплопроводности, или Уравнения Навье-Стокса выражается либо в PDE, либо в интегральные уравнения, в то время как разделенные мелкие элементы сложной проблемы представляют различные области физической системы.
FEA - хороший выбор для анализа проблем в сложных областях (таких как автомобили и нефтепроводы), когда область изменяется (как во время твердотельной реакции с движущейся границей), когда желаемая точность изменяется во всей области или когда раствору не хватает гладкости. Моделирование методом FEA является ценным ресурсом, поскольку устраняет несколько экземпляров создания и тестирования твердых прототипов для различных ситуаций с высокой точностью воспроизведения.[3] Например, при моделировании лобового столкновения можно повысить точность прогнозирования в «важных» областях, таких как передняя часть автомобиля, и уменьшить ее в задней части (таким образом, снижая стоимость моделирования). Другой пример был бы в численный прогноз погоды, где более важно иметь точные прогнозы развития сильно нелинейных явлений (таких как тропические циклоны в атмосфере, или водовороты в океане), а не в относительно спокойных районах.
История
Хотя трудно назвать дату изобретения метода конечных элементов, этот метод возник из-за необходимости решать сложные эластичность и структурный анализ проблемы в гражданский и авиационная техника. Его развитие можно проследить до работы А. Хренникофф[4] и Р. Курант[5] в начале 1940-х гг. Другой пионер был Иоаннис Аргирис. В СССР внедрение метода в практику обычно связывают с именем Леонард Оганесян.[6] В Китае в конце 1950-х - начале 1960-х годов, исходя из расчетов строительства плотин, К. Фэн предложил систематический численный метод решения уравнения в частных производных. Метод получил название метод конечных разностей, основанный на вариационном принципе, который был еще одним независимым изобретением метода конечных элементов.[7] Хотя подходы, используемые этими пионерами, различны, у них есть одна важная характеристика: сетка дискретизация непрерывной области в набор дискретных подобластей, обычно называемых элементами.
Работа Хренникова дискретизирует область с помощью решетка аналогии, в то время как подход Куранта делит область на конечные треугольные подобласти для решения второго порядка эллиптический уравнения в частных производных (PDE), возникающие из проблемы кручение из цилиндр. Вклад Куранта был эволюционным, он опирался на большое количество более ранних результатов для PDE, разработанных Рэлей, Ритц, и Галеркин.
Настоящее развитие метод конечных элементов получил в 1960-х и 1970-х годах благодаря разработкам Дж. Х. Аргирис с коллегами по Штутгартский университет, Р. В. Клаф с коллегами по Калифорнийский университет в Беркли, О. К. Зенкевич с коллегами Эрнест Хинтон, Брюс Айронс[8] и другие на Суонси университет, Филипп Ж. Сиарле в университете Париж 6 и Ричард Галлахер с коллегами из Корнелл Университет. Дальнейший импульс в эти годы был придан доступным программам конечных элементов с открытым кодом. НАСА спонсировало оригинальную версию NASTRAN, а Калифорнийский университет в Беркли создал программу конечных элементов SAP IV[9] широко доступный. В Норвегии классификационное общество судов Det Norske Veritas (ныне DNV GL) развитый Sesam в 1969 г. для использования при анализе кораблей.[10] Строгая математическая основа метода конечных элементов была предоставлена в 1973 г. с публикацией автора Strang и Исправить.[11] С тех пор метод был обобщен для численное моделирование физических систем в самых разных инженерное дело дисциплины, например, электромагнетизм, теплопередача, и динамика жидкостей.[12][13]
Техническое обсуждение
Структура методов конечных элементов
Метод конечных элементов характеризуется вариационная формулировка, стратегия дискретизации, один или несколько алгоритмов решения и процедуры постобработки.
Примеры вариационной постановки: Метод Галеркина, разрывный метод Галеркина, смешанные методы и др.
Под стратегией дискретизации понимается четко определенный набор процедур, которые охватывают (а) создание сеток из конечных элементов, (б) определение базовой функции на опорных элементах (также называемых функциями формы) и (в) отображение опорных элементы на элементы сетки. Примерами стратегий дискретизации являются h-версия, p-версия, hp-версия, x-FEM, изогеометрический анализи др. Каждая стратегия дискретизации имеет определенные преимущества и недостатки. Разумным критерием при выборе стратегии дискретизации является достижение почти оптимальной производительности для самого широкого набора математических моделей в конкретном классе моделей.
Различные алгоритмы численного решения можно разделить на две большие категории; прямые и итерационные решатели. Эти алгоритмы предназначены для использования разреженности матриц, зависящих от выбора вариационной формулировки и стратегии дискретизации.
Процедуры постобработки предназначены для извлечения интересующих данных из решения методом конечных элементов. Чтобы соответствовать требованиям проверки решения, постпроцессорам необходимо предусмотреть апостериорный оценка ошибки с точки зрения интересующих количеств. Когда ошибки аппроксимации больше, чем считается приемлемым, дискретизация должна быть изменена либо автоматизированным адаптивным процессом, либо действием аналитика. Есть несколько очень эффективных постпроцессоров, которые обеспечивают реализацию сверхконвергенция.
Иллюстративные задачи P1 и P2
Мы продемонстрируем метод конечных элементов на двух примерах задач, из которых можно экстраполировать общий метод. Предполагается, что читатель знаком с исчисление и линейная алгебра.
P1 - это одномерный проблема
где дано, неизвестная функция , и - вторая производная от относительно .
P2 - это двумерный проблема (Задача Дирихле)
где - связная открытая область в плоскость, граница которой хорошо (например, гладкое многообразие или многоугольник), и и обозначим вторые производные по и , соответственно.
Задачу P1 можно решить напрямую, вычислив первообразные. Однако этот метод решения краевая задача (BVP) работает только тогда, когда существует одно пространственное измерение, и не распространяется на проблемы более высокого измерения или проблемы, такие как . По этой причине мы разработаем метод конечных элементов для P1 и опишем его обобщение для P2.
Наше объяснение состоит из двух шагов, которые отражают два важных шага, которые необходимо предпринять для решения краевой задачи (BVP) с использованием FEM.
- На первом этапе мы перефразируем исходный BVP в его слабой форме. Для этого шага обычно не требуется никаких вычислений. Преобразование выполняется вручную на бумаге.
- Второй шаг - это дискретизация, когда слабая форма дискретизируется в конечномерном пространстве.
После этого второго шага у нас есть конкретные формулы для большой, но конечномерной линейной задачи, решение которой приближенно решает исходную BVP. Затем эта конечномерная задача реализуется на компьютер.
Слабая формулировка
Первый шаг - преобразовать P1 и P2 в их эквивалент. слабые составы.
Слабая форма P1
Если решает P1, то для любой гладкой функции который удовлетворяет граничным условиям перемещения, т. е. в и , у нас есть
(1)
Наоборот, если с удовлетворяет (1) для любой гладкой функции тогда можно показать, что это решит P1. Доказательство легче для дважды непрерывно дифференцируемых (теорема о среднем значении), но может быть доказано в распределительный смысл тоже.
Определяем новый оператор или карту используя интеграция по частям в правой части (1):
(2)
где мы использовали предположение, что .
Слабая форма P2
Если мы интегрируем по частям, используя форму Личность Грина, мы видим, что если решает P2, то мы можем определить для любого к
где обозначает градиент и обозначает скалярное произведение в двумерной плоскости. Еще раз можно превратить в внутренний продукт на подходящем месте некогда дифференцируемых функций которые равны нулю на . Мы также предположили, что (увидеть Соболевские пространства). Также можно показать существование и уникальность решения.
Схема доказательства существования и единственности решения
Мы можем свободно думать о быть абсолютно непрерывный функции которые в и (увидеть Соболевские пространства). Такие функции (слабо) однократно дифференцируемы, и оказывается, что симметричная билинейная карта затем определяет внутренний продукт что превращает в Гильбертово пространство (подробное доказательство нетривиально). С другой стороны, левая сторона также внутренний продукт, на этот раз на Lp пространство . Приложение Теорема Рисса о представлении для гильбертовых пространств показывает, что существует единственная решение (2) и, следовательно, P1. Это решение является априори только членом , но используя эллиптический регулярность, будет плавной, если является.
Дискретность
P1 и P2 готовы к дискретизации, что приводит к общей подзадаче (3). Основная идея - заменить бесконечномерную линейную задачу:
- Находить такой, что
с конечномерной версией:
- (3) Найти такой, что
где является конечномерным подпространство из . Есть много возможных вариантов (одна возможность приводит к спектральный метод). Однако для метода конечных элементов мы берем быть пространством кусочно-полиномиальных функций.
Для задачи P1
Берем интервал , выберите ценности с и мы определяем от:
где мы определяем и . Обратите внимание, что функции в не дифференцируемы согласно элементарному определению исчисления. Действительно, если то производная обычно не определяется ни на каком , . Однако производная существует при любом другом значении и можно использовать эту производную с целью интеграция по частям.
Для задачи P2
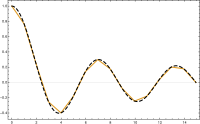
Нам нужно быть набором функций . На рисунке справа мы проиллюстрировали триангуляция 15-стороннего многоугольный область, край в плоскости (внизу), а кусочно-линейная функция (вверху в цвете) этого многоугольника, который является линейным на каждом треугольнике триангуляции; космос будет состоять из функций, линейных на каждом треугольнике выбранной триангуляции.
Можно надеяться, что по мере того, как нижележащая треугольная сетка становится все более и более тонкой, решение дискретной задачи (3) в каком-то смысле сходится к решению исходной краевой задачи P2. Чтобы измерить тонкость этой сетки, триангуляция индексируется параметром с действительным знаком. который считается очень маленьким. Этот параметр будет связан с размером самого большого или среднего треугольника в триангуляции. При уточнении триангуляции пространство кусочно-линейных функций также должен измениться с . По этой причине часто читают вместо того в литературе. Поскольку мы не проводим такой анализ, мы не будем использовать эти обозначения.
Выбор основы
Чтобы завершить дискретизацию, мы должны выбрать основа из . В одномерном случае для каждой контрольной точки выберем кусочно-линейную функцию в чья ценность в и ноль на каждом , т.е.
за ; эта основа сдвинута и масштабирована функция палатки. Для двумерного случая снова выбираем одну базисную функцию на вершину триангуляции плоской области . Функция уникальная функция чья ценность в и ноль на каждом .
В зависимости от автора слово «элемент» в «методе конечных элементов» относится либо к треугольникам в области, либо к кусочно-линейной базисной функции, либо к обоим. Так, например, автор, интересующийся изогнутыми доменами, может заменить треугольники изогнутыми примитивами и, таким образом, описать элементы как криволинейные. С другой стороны, некоторые авторы заменяют «кусочно линейный» на «кусочно-квадратичный» или даже «кусочно-полиномиальный». Тогда автор мог бы сказать «элемент более высокого порядка» вместо «полином более высокой степени». Метод конечных элементов не ограничен треугольниками (или тетраэдрами в трехмерном пространстве, или симплексами более высокого порядка в многомерных пространствах), но может быть определен в четырехугольных подобластях (шестигранники, призмы или пирамиды в трехмерном пространстве и т. Д.) . Формы более высокого порядка (криволинейные элементы) могут быть определены с помощью полиномиальных и даже неполиномиальных форм (например, эллипса или круга).
Примеры методов, использующих кусочно-полиномиальные базисные функции более высокой степени:hp-FEM и спектральный МКЭ.
Более продвинутые реализации (адаптивные методы конечных элементов) используют метод оценки качества результатов (на основе теории оценки ошибок) и модифицируют сетку во время решения, стремясь достичь приближенного решения в некоторых пределах от точного решения задачи континуума. . Адаптивная сетка может использовать различные методы, наиболее популярными из которых являются:
- движущиеся узлы (r-адаптивность)
- уточняющие (и необработанные) элементы (h-адаптивность)
- изменение порядка базовых функций (p-адаптивность)
- комбинации вышеперечисленного (hp-адаптивность).
Малая опора основания

Основное преимущество такого выбора основы состоит в том, что внутренние продукты
и
будет нулем почти для всех . (Матрица, содержащая в место известно как Матрица грамиана.) В одномерном случае поддержка из это интервал . Следовательно, подынтегральные выражения и тождественно равны нулю всякий раз, когда .
Аналогично в плоском случае, если и не имеют общего ребра триангуляции, то интегралы
и
оба равны нулю.
Матричная форма задачи
Если мы напишем и то задача (3), взяв за , становится
- за (4)
Если обозначить через и вектор-столбец и , и если мы позволим
и
- матрицы, элементы которых
и
тогда мы можем перефразировать (4) как
- (5)
Не нужно предполагать . Для общей функции , задача (3) с за становится проще, поскольку нет матрицы используется,
- , (6)
где и за .
Как мы уже обсуждали ранее, большинство записей и равны нулю, поскольку базисные функции есть небольшая поддержка. Итак, теперь нам нужно решить линейную систему в неизвестном где большинство элементов матрицы , которые нам нужно инвертировать, равны нулю.
Такие матрицы известны как разреженные матрицы, и есть эффективные средства решения таких проблем (гораздо более эффективные, чем фактическое обращение матрицы). Кроме того, симметрична и положительно определена, поэтому такая техника, как метод сопряженных градиентов одобрено. Для задач, которые не слишком большие, редкие LU разложения и Разложения Холецкого все еще хорошо работает. Например, MATLABОператора обратной косой черты (который использует разреженный LU, разреженный метод Холецкого и другие методы факторизации) может быть достаточно для сеток с сотней тысяч вершин.
Матрица обычно называют матрица жесткости, а матрица называется матрица масс.
Общий вид метода конечных элементов
В целом метод конечных элементов характеризуется следующим процессом.
- Выбирают сетку для . В предыдущем рассмотрении сетка состояла из треугольников, но также можно использовать квадраты или криволинейные многоугольники.
- Затем выбираются базисные функции. В нашем обсуждении мы использовали кусочно-линейные базисные функции, но также часто используются кусочно-полиномиальные базисные функции.
Отдельное внимание уделяется гладкости базисных функций. Для второго порядка эллиптические краевые задачи, кусочно-полиномиальная базисная функция, которая является просто непрерывной (т. е. производные разрывны). Для уравнений в частных производных более высокого порядка необходимо использовать более гладкие базисные функции. Например, для задачи четвертого порядка, такой как , можно использовать кусочно-квадратичные базисные функции, которые .
Еще одно соображение - это связь конечномерного пространства своему бесконечномерному аналогу, в примерах выше . А метод соответствующего элемента тот, в котором пространство является подпространством пространства элементов непрерывной задачи. Пример выше - такой метод. Если это условие не выполняется, получаем метод несоответствующего элемента, примером которого является пространство кусочно-линейных функций над сеткой, непрерывных в каждой средней точке ребра. Поскольку эти функции, вообще говоря, разрывны по ребрам, это конечномерное пространство не является подпространством исходного .
Обычно у каждого есть алгоритм для взятия заданной сетки и ее разделения. Если основным методом повышения точности является разбиение сетки на части, получается час-метод (час обычно является диаметром самого большого элемента в сетке.) Таким образом, если кто-то показывает, что ошибка с сеткой ограничен сверху , для некоторых и , то есть заказ п метод. При определенных предположениях (например, если область выпуклая) кусочно-полином порядка метод будет иметь ошибку порядка .
Если вместо того, чтобы делать час чем меньше, тем выше степень полиномов, используемых в базисной функции, п-метод. Если объединить эти два типа уточнения, получится л.с.-метод (hp-FEM). В hp-FEM степени полинома могут варьироваться от элемента к элементу. Методы высокого порядка с большой униформой п называются спектральными методами конечных элементов (SFEM). Их не следует путать с спектральные методы.
Для векторных уравнений в частных производных базисные функции могут принимать значения в .
Различные типы методов конечных элементов
AEM
Метод прикладных элементов или AEM сочетает в себе функции как FEM, так и Метод дискретных элементов, или (DEM).
Обобщенный метод конечных элементов
Обобщенный метод конечных элементов (GFEM) использует локальные пространства, состоящие из функций, не обязательно полиномов, которые отражают доступную информацию о неизвестном решении и, таким образом, обеспечивают хорошее локальное приближение. Потом разделение единства используется, чтобы «связать» эти пространства вместе, чтобы сформировать аппроксимирующее подпространство. Эффективность GFEM была показана при применении к задачам с областями со сложными границами, задачам с микромасштабами и задачам с пограничными слоями.[14]
Смешанный метод конечных элементов
Смешанный метод конечных элементов - это тип метода конечных элементов, в котором дополнительные независимые переменные вводятся как узловые переменные во время дискретизации задачи уравнения в частных производных.
Переменная - полиномиальная
В hp-FEM адаптивно комбинирует элементы с переменным размером час и степень полинома п для достижения исключительно быстрой экспоненциальной скорости сходимости.[15]
HPK-FEM
В HPK-FEM адаптивно комбинирует элементы с переменным размером час, полиномиальная степень локальных приближений п и глобальная дифференцируемость локальных приближений (к-1) для достижения наилучших показателей сходимости.
XFEM
В расширенный метод конечных элементов (XFEM) - это численный метод, основанный на обобщенном методе конечных элементов (GFEM) и методе разделения единицы (PUM). Он расширяет классический метод конечных элементов, обогащая пространство решений для решений дифференциальных уравнений с разрывными функциями. Расширенные методы конечных элементов обогащают пространство аппроксимации, так что оно может естественным образом воспроизводить сложные особенности, связанные с интересующей проблемой: разрыв, сингулярность, пограничный слой и т. Д. Было показано, что для некоторых задач такое вложение признака задачи в пространство аппроксимации может значительно улучшить скорость сходимости и точность. Более того, обработка проблем с неоднородностями с помощью XFEM устраняет необходимость в сетке и повторной сетке поверхностей неоднородностей, тем самым уменьшая вычислительные затраты и ошибки проекции, связанные с традиционными методами конечных элементов, за счет ограничения несплошностей краями сетки.
Несколько исследовательских кодов реализуют этот метод в различной степени: 1. GetFEM ++ 2. xfem ++ 3. openxfem ++
XFEM также был реализован в таких кодах, как Altair Radios, ASTER, Morfeo и Abaqus. Он все чаще внедряется в другое коммерческое программное обеспечение конечных элементов с несколькими доступными плагинами и фактическими реализациями ядра (ANSYS, SAMCEF, OOFELIE и т. Д.).
Метод масштабированных граничных конечных элементов (SBFEM)
Введение метода масштабированных граничных конечных элементов (SBFEM) было предложено Сонг и Вольфом (1997).[16] SBFEM был одним из самых прибыльных достижений в области численного анализа проблем механики разрушения. Это полуаналитический метод без фундаментальных решений, который сочетает в себе преимущества формулировок и процедур конечных элементов, а также дискретизации граничных элементов. Однако, в отличие от метода граничных элементов, не требуется фундаментального дифференциального решения.
S-FEM
S-FEM, сглаженные методы конечных элементов, представляют собой особый класс алгоритмов численного моделирования для моделирования физических явлений. Он был разработан путем объединения бессеточных методов с методом конечных элементов.
Метод спектральных элементов
Методы спектральных элементов сочетают геометрическую гибкость конечных элементов и высокую точность спектральных методов. Спектральные методы представляют собой приближенное решение уравнений в частных слабых формах, основанных на лагранжевых интерполянтах высокого порядка и используемых только с определенными квадратурными правилами.[17]
Meshfree методы
Разрывные методы Галеркина
Анализ предела конечных элементов
Метод растянутой сетки
Итерация Лабиньяка
Итерация Лабиньяка является итерационным методом в методах конечных элементов.
Связь с методом градиентной дискретизации
Некоторые типы методов конечных элементов (согласующиеся, несоответствующие, смешанные методы конечных элементов) являются частными случаями метод градиентной дискретизации (GDM). Следовательно, свойства сходимости GDM, которые установлены для ряда задач (линейные и нелинейные эллиптические задачи, линейные, нелинейные и вырожденные параболические задачи), также сохраняются для этих конкретных методов конечных элементов.
Сравнение с методом конечных разностей
Эта секция не цитировать любой источники. (Ноябрь 2010 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В метод конечных разностей (FDM) - альтернативный способ аппроксимации решений PDE. Различия между FEM и FDM:
- Наиболее привлекательной особенностью FEM является его способность относительно легко обрабатывать сложные геометрические формы (и границы). В то время как FDM в своей базовой форме ограничивается обработкой прямоугольных форм и их простых изменений, обработка геометрических фигур в FEM теоретически проста.
- FDM обычно не используется для нестандартных геометрических форм САПР, а чаще используется для прямоугольных или блочных моделей.[18]
- Самая привлекательная особенность конечных разностей заключается в том, что их очень легко реализовать.
- Есть несколько способов рассматривать FDM как частный случай подхода FEM. Например, FEM первого порядка идентичен FDM для Уравнение Пуассона, если проблема в дискретизированный правильной прямоугольной сеткой, каждый прямоугольник которой разделен на два треугольника.
- Есть причины считать математическую основу аппроксимации методом конечных элементов более надежной, например, потому, что качество аппроксимации между точками сетки в FDM оставляет желать лучшего.
- Качество приближения FEM часто выше, чем в соответствующем подходе FDM, но это очень проблемно-зависимо, и можно привести несколько примеров обратного.
Как правило, МКЭ - это метод выбора во всех типах анализа в строительной механике (т. Е. Решение для деформации и напряжений в твердых телах или динамики конструкций), в то время как вычислительная гидродинамика (CFD), как правило, используют FDM или другие методы, например метод конечных объемов (FVM). Задачи CFD обычно требуют дискретизации задачи на большое количество ячеек / точек сетки (миллионы и более), поэтому стоимость решения способствует более простой аппроксимации более низкого порядка в каждой ячейке. Это особенно верно для проблем с «внешним потоком», таких как воздушный поток вокруг автомобиля или самолета или моделирование погоды.
Заявление

Различные специализации в рамках дисциплины машиностроения (например, авиационная, биомеханическая и автомобильная промышленность) обычно используют интегрированные FEM при проектировании и разработке своих продуктов. Несколько современных пакетов FEM включают специальные компоненты, такие как тепловые, электромагнитные, жидкостные и структурные рабочие среды. В структурном моделировании FEM очень помогает в визуализации жесткости и прочности, а также в минимизации веса, материалов и затрат.[19]
FEM позволяет детально визуализировать изгиб или скручивание конструкций, а также показывает распределение напряжений и смещений. Программное обеспечение FEM предоставляет широкий спектр возможностей моделирования для управления сложностью моделирования и анализа системы. Точно так же можно одновременно управлять желаемым уровнем требуемой точности и соответствующими требованиями к вычислительному времени для решения большинства инженерных приложений. FEM позволяет конструировать, уточнять и оптимизировать целые конструкции до того, как они будут изготовлены. Сетка является неотъемлемой частью модели, и для получения наилучших результатов необходимо тщательно контролировать ее. Как правило, чем больше количество элементов в сетке, тем точнее решение дискретизированной задачи. Однако существует значение, при котором результаты сходятся, и дальнейшее уточнение сетки не увеличивает точность.[20]

Этот мощный инструмент проектирования значительно улучшил стандарты проектирования и методологию проектирования во многих промышленных приложениях.[22] Внедрение FEM существенно сократило время, необходимое для вывода продуктов от концепции до производственной линии.[22] Тестирование и разработка были ускорены в первую очередь за счет улучшенных первоначальных прототипов с использованием МКЭ.[23] Таким образом, преимущества FEM включают повышенную точность, улучшенный дизайн и лучшее понимание критических параметров конструкции, виртуальное прототипирование, меньшее количество аппаратных прототипов, более быстрый и менее затратный цикл проектирования, повышенную производительность и увеличение доходов.[22]
В 1990-х годах метод FEA был предложен для использования в стохастическом моделировании для численного решения вероятностных моделей.[24] а затем для оценки надежности.[25]
Смотрите также
- Метод прикладного элемента
- Метод граничных элементов
- Лемма Сеа
- Компьютерный эксперимент
- Метод прямой жесткости
- Оптимизация компоновки разрывов
- Метод дискретных элементов
- Метод конечных разностей
- Машина конечных элементов
- Метод конечных элементов в строительной механике
- Метод конечных объемов
- Метод конечных объемов для нестационарного потока
- Метод бесконечных элементов
- Интервальный конечный элемент
- Изогеометрический анализ
- Решеточные методы Больцмана
- Список пакетов программного обеспечения конечных элементов
- Meshfree методы
- Подвижный клеточный автомат
- Междисциплинарная оптимизация дизайна
- Мультифизика
- Патч-тест
- Метод Рэлея – Ритца
- Картирование космоса
- Тесселяция (компьютерная графика)
- Ослабленная слабая форма
Рекомендации
- ^ Дэрил Л. Логан (2011). Первый курс по методу конечных элементов. Cengage Learning. ISBN 978-0495668251.
- ^ Редди, Дж. Н. (2006). Введение в метод конечных элементов (Третье изд.). Макгроу-Хилл. ISBN 9780071267618.
- ^ «Анализ методом конечных элементов (FEA)». www.manortool.com. Получено 2017-07-28.
- ^ Хренникофф, Александр (1941). «Решение задач упругости каркасным методом». Журнал прикладной механики. 8 (4): 169–175.
- ^ Курант Р. (1943). «Вариационные методы решения задач равновесия и колебаний». Бюллетень Американского математического общества. 49: 1–23. Дои:10.1090 / s0002-9904-1943-07818-4.
- ^ "СПб ЭМИ РАН". emi.nw.ru. Архивировано из оригинал 30 сентября 2015 г.. Получено 17 марта 2018.
- ^ «Кан Фэн» (PDF). CAS.
- ^ Хинтон, Эрнест; Айронс, Брюс (июль 1968 г.). «Сглаживание экспериментальных данных методом наименьших квадратов с использованием конечных элементов». Напряжение. 4 (3): 24–27. Дои:10.1111 / j.1475-1305.1968.tb01368.x.
- ^ «Программное обеспечение и руководства SAP-IV». Электронная библиотека NISEE, Интернет-архив сейсмологической инженерии.
- ^ Гард Паулсен; Хокон с Андерсеном; Джон Петтер Коллетт; Ивер Танген Стенсруд (2014). Building Trust, История DNV 1864-2014. Лисакер, Норвегия: Dinamo Forlag A / S. С. 121, 436. ISBN 978-82-8071-256-1.
- ^ Стрэнг, Гилберт; Исправить, Джордж (1973). Анализ метода конечных элементов. Прентис Холл. ISBN 978-0-13-032946-2.
- ^ Олек Зенкевич; Роберт Л. Тейлор; J.Z. Чжу (31 августа 2013 г.). Метод конечных элементов: его основы и основы. Баттерворт-Хайнеманн. ISBN 978-0-08-095135-5.
- ^ Купайся, К.Дж. (2006). Процедуры с конечными элементами. Кембридж, Массачусетс: Клаус-Юрген Бат. ISBN 978-0979004902.
- ^ Бабушка, Иво; Банерджи, Удай; Осборн, Джон Э. (Июнь 2004 г.). «Обобщенные методы конечных элементов: основные идеи, результаты и перспективы». Международный журнал вычислительных методов. 1 (1): 67–103. Дои:10.1142 / S0219876204000083.
- ^ П. Солин, К. Сегет, И. Долезель: Методы конечных элементов высшего порядка, Chapman & Hall / CRC Press, 2003
- ^ Песня, Чонгмин; Вольф, Джон П. (5 августа 1997 г.). «Метод конечных элементов с масштабированной границей - псевдоним последовательного метода бесконечно малых конечных элементов - для эластодинамики». Компьютерные методы в прикладной механике и технике. 147 (3–4): 329–355. Bibcode:1997CMAME.147..329S. Дои:10.1016 / S0045-7825 (97) 00021-2.
- ^ «Методы спектральных элементов». Государственная ключевая лаборатория научных и инженерных вычислений. Получено 2017-07-28.
- ^ «В чем разница между FEM, FDM и FVM?». Дизайн машины. 2016-04-18. Получено 2017-07-28.
- ^ Кирицис, Д .; Eemmanouilidis, Ch .; Koronios, A .; Мэтью, Дж. (2009). «Инженерное управление активами». Материалы 4-го Всемирного конгресса по управлению инженерными активами (WCEAM): 591–592.
- ^ «Конечно-элементный анализ: как создать отличную модель». Ковентивные композиты. 2019-03-18. Получено 2019-04-05.
- ^ Нагиби Бейдохти, Хамид; Янссен, Деннис; Хошгофтар, Мехди; Спренгерс, Андре; Пердахчоглу, Эмин Семих; Boogaard, Тон Ван ден; Вердоншот, Нико (2016). «Сравнение динамического неявного и явного моделирования методом конечных элементов собственного коленного сустава» (PDF). Медицинская инженерия и физика. 38 (10): 1123–1130. Дои:10.1016 / j.medengphy.2016.06.001. PMID 27349493.
- ^ а б c Гастингс, Дж. К., Джадс, М. А., Брауэр, Дж. Р., Точность и экономичность конечно-элементного магнитного анализа, 33-я ежегодная национальная эстафетная конференция, апрель 1985 г.
- ^ Макларен-Мерседес (2006 г.). «McLaren Mercedes: особенность - стресс, чтобы произвести впечатление». Архивировано из оригинал на 2006-10-30. Получено 2006-10-03.
- ^ Пэн Лун; Ван Цзиньлян; Чжу Цидин (19 мая 1995 г.). «Методы с высокой точностью для вычисления вероятностей конечных элементов». Журнал вычислительной и прикладной математики. 59 (2): 181–189. Дои:10.1016 / 0377-0427 (94) 00027-X.
- ^ Халдар, Ачинтья; Махадеван, Шанкаран (2000). Оценка надежности с использованием стохастического конечно-элементного анализа. Джон Вили и сыновья. ISBN 978-0471369615.
дальнейшее чтение
- Г. Аллер и А. Крейг: Численный анализ и оптимизация: введение в математическое моделирование и численное моделирование.
- К. Дж. Бат: Численные методы в конечно-элементном анализе, Прентис-Холл (1976).
- Томас Дж. Р. Хьюз: Метод конечных элементов: линейный статический и динамический анализ конечных элементов, Прентис-Холл (1987).
- Я. Часкалович: Методы конечных элементов для технических наук, Springer Verlag, (2008).
- Эндре Сюли: Методы конечных элементов для уравнений с частными производными.
- О. К. Зенкевич, Р. Л. Тейлор, Дж. З. Чжу: Метод конечных элементов: его основы и основы, Баттерворт-Хайнеманн (2005).
внешняя ссылка
| Викискладе есть медиафайлы по теме Конечно-элементное моделирование. |
- IFER - Интернет-ресурсы по конечным элементам - описывает и предоставляет доступ к программному обеспечению для анализа методом конечных элементов через Интернет
- NAFEMS - Международная ассоциация инженерного моделирования
- Математика метода конечных элементов















































![{displaystyle V = {v: [0,1] ightarrow mathbb {R};: v {mbox {непрерывно,}} v | _ {[x_ {k}, x_ {k + 1}]} {mbox {это линейный для}} k = 0, точек, n {mbox {, и}} v (0) = v (1) = 0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d72f354ee5b50866296ad9e758f442f6a32d4b32)









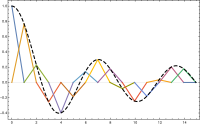




![v_ {k} (x) = egin {case} {x-x_ {k-1} over x_k, -x_ {k-1}} & mbox {if} x in [x_ {k-1}, x_k],
{x_ {k + 1}, - x больше x_ {k + 1}, - x_k} & mbox {if} x в [x_k, x_ {k + 1}],
0 & mbox {else}, конец {case}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1d8df33dbf412ea446944402c80c7cab51ecd7e)










![[x_ {k-1}, x_ {k + 1}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9ab905e7068db95aeddfd9f0fa55af0e0363843)



































