WikiDer > Моноидальная категория
В математика, а моноидальная категория (или же тензорная категория) это категория оснащен бифунктор
то есть ассоциативный вплоть до а естественный изоморфизм, и объект я это одновременно оставили и правильная личность для снова с точностью до естественного изоморфизма. Соответствующие естественные изоморфизмы подчиняются определенным условия согласованности, которые обеспечивают коммутацию всех соответствующих диаграмм.
Обычный тензорное произведение делает векторные пространства, абелевы группы, р-модули, или же р-алгебры на моноидальные категории. Моноидальные категории можно рассматривать как обобщение этих и других примеров. Каждую (небольшую) моноидальную категорию можно также рассматривать как "категоризация"основного моноид, а именно моноид, элементы которого являются классами изоморфизма объектов категории и чья бинарная операция задается тензорным произведением категории.
Совсем другое приложение, в котором моноидальные категории можно рассматривать как абстракцию, - это система типы данных закрыт под конструктор типов который принимает два типа и строит агрегатный тип; типы - это объекты и является агрегатным конструктором. Тогда ассоциативность с точностью до изоморфизма - это способ выразить разные способы агрегирования одних и тех же данных, например и - хранить одну и ту же информацию, даже если совокупные значения не должны совпадать. Объекты идентичности аналогичны алгебраическим операциям сложения (тип сумма) и умножения (тип произведения). Для типа продукт - объект идентичности - единица , он тривиально полностью населяет свой тип, поэтому существует только один обитатель этого типа, и поэтому продукт с ним всегда изоморфен другому операнду. Для типа sum объектом идентификации является тип пустоты, который не хранит никакой информации, и к его обитателям невозможно обратиться. Концепция моноидальной категории не предполагает, что значения таких агрегированных типов могут быть разделены; напротив, он обеспечивает основу, объединяющую классические и квантовая информация теория.[1]
В теория категорий, моноидальные категории могут быть использованы для определения понятия моноидный объект и связанное действие с объектами категории. Они также используются в определении обогащенная категория.
Моноидальные категории имеют множество приложений за пределами собственно теории категорий. Они используются для определения моделей мультипликативного фрагмента интуиционистский линейная логика. Они также образуют математическую основу для топологический порядок в конденсированных средах. Плетеные моноидальные категории иметь приложения в квантовая информация, квантовая теория поля, и теория струн.
Формальное определение
А моноидальная категория это категория оснащен моноидальной структурой. Моноидальная структура состоит из следующего:
- а бифунктор называется тензорное произведение или же моноидальный продукт,
- объект называется единичный объект или же объект идентичности,
- три естественные изоморфизмы при соблюдении определенных условия согласованности выражая тот факт, что тензорная операция
- ассоциативно: существует естественный (в каждом из трех аргументов , , ) изоморфизм , называется ассоциатор, с компонентами ,
- имеет как левое и правое тождество: есть два естественных изоморфизма и соответственно называется оставили и правый объединитель, с компонентами и .
Обратите внимание, что это хороший способ запомнить, как и действие осуществляется аллитерацией; Лямбда, , отменяет идентификацию на оставили, пока Ро, , отменяет идентификацию на верно.
Условиями согласованности этих естественных преобразований являются:
- для всех , , и в , пятиугольник диаграмма
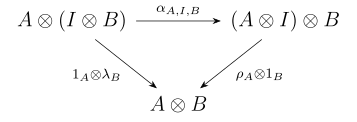
- для всех и в , треугольная диаграмма
- ездит на работу.
А строгая моноидальная категория тот, для которого естественные изоморфизмы α, λ и ρ идентичности. Каждая моноидальная категория моноидально эквивалент к строгой моноидальной категории.
Примеры
- Любая категория с конечным товары можно рассматривать как моноидальный, причем произведение является моноидальным произведением, а конечный объект как единица. Такую категорию иногда называют декартова моноидальная категория. Например:
- Набор, то категория наборов с декартовым произведением - любой конкретный одноэлементный набор, служащий единицей.
- Кот, категория малых категорий с Категория продукта, где единицей является категория с одним объектом и только его идентификационной картой.
- Двойственно любая категория с конечным побочные продукты является моноидальным с сопродуктом как моноидальным произведением и исходный объект как единица. Такая моноидальная категория называется кокартово моноидальный
- р-Мод, то категория модулей через коммутативное кольцо р, является моноидальной категорией с тензорное произведение модулей ⊗р служащий моноидальным произведением и кольцом р (воспринимается как модуль над собой), выступающий в качестве единицы. К особым случаям относятся:
- K-Вект, то категория векторных пространств через поле K, с одномерным векторным пространством K служащий единицей.
- Ab, то категория абелевых групп, с группой целые числа Z служащий единицей.
- Для любого коммутативного кольца р, категория р-алгебры моноидален с тензорное произведение алгебр как продукт и р как единица.
- В категория остроконечных пространств (ограниченный компактно порожденные пространства например) моноидален с разбить продукт служащий продуктом и острым 0-сфера (двухточечное дискретное пространство), выступающее в качестве единицы.
- Категория всех эндофункторы по категории C это строгий моноидальная категория с композицией функторов как произведения и тождественного функтора как единицы.
- Как и для любой категории E, то полная подкатегория натянутый на любой данный объект является моноидом, это так, что для любого 2 категории E, и любой объект C в Оби (E), полная 2-подкатегория E охватывает {C} - моноидальная категория. В случае E = Кот, мы получаем эндофункторы пример выше.
- Ограниченные сверху пересекаются полурешетки строгие симметричные моноидальные категории: продукт соответствует, а идентичность - это главный элемент.
- Любой обычный моноид это небольшая моноидальная категория с набором объектов , только идентичности для морфизмы, как тензорное произведение и как объект идентичности. И наоборот, множество классов изоморфизма (если в этом есть смысл) моноидальной категории является моноидом относительно. тензорное произведение.
Моноидальные предзаказы
В этом разделе тон или стиль могут не отражать энциклопедический тон используется в Википедии. (Март 2017 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Моноидальные предзаказы, также известные как «предупорядоченные моноиды», являются частными случаями моноидальных категорий. Такая структура возникает в теории системы перезаписи строк, но и в чистой математике его много. Например, набор из натуральные числа имеет как моноидная структура (используя + и 0) и структура предварительного заказа (используя ≤), которые вместе образуют моноидальный предварительный заказ, в основном потому, что и подразумевает . Приведем теперь общий случай.
Хорошо известно, что Предварительный заказ можно рассматривать как категорию C, так что для каждых двух объектов , Существует максимум один морфизм в C. Если случится морфизм от c к c ' , мы могли бы написать , но в этом разделе нам удобнее выразить этот факт в виде стрелки . Поскольку существует не более одного такого морфизма, нам никогда не нужно давать ему имя, например . В рефлексивность и транзитивность свойства порядка соответственно учитываются тождественным морфизмом и формулой композиции в C. Мы пишем если только и , т.е. если они изоморфны в C. Обратите внимание, что в частичный заказ, любые два изоморфных объекта фактически равны.
Двигаясь вперед, предположим, что мы хотим добавить моноидальную структуру к предзаказу. C. Для этого мы должны выбрать
- объект , называется моноидальный блок, и
- функтор , который мы будем обозначать просто точкой "", называется моноидальное умножение.
Таким образом, для любых двух объектов у нас есть объект . Мы должны выбрать и быть ассоциативным и унитальным, с точностью до изоморфизма. Это означает, что мы должны иметь:
- и .
Более того, тот факт, что · требуется, чтобы быть функтором, означает - в данном случае, когда C является предварительным заказом и не более того:
- если и тогда .
Дополнительные условия когерентности для моноидальных категорий в этом случае бессмысленны, потому что каждая диаграмма коммутирует в предпорядке.
Обратите внимание, что если C является частичным порядком, приведенное выше описание упрощено еще больше, потому что изоморфизмы ассоциативности и унитальности становятся равенствами. Другое упрощение происходит, если мы предполагаем, что набор объектов является свободный моноид на генераторной установке . В этом случае мы могли бы написать , где * обозначает Клини звезда и моноидальный блок я обозначает пустую строку. Если мы начнем с набора р порождающих морфизмов (факты о ≤), мы восстанавливаем обычное понятие система полутхуэ, куда р называется «правилом перезаписи».
Чтобы вернуться к нашему примеру, пусть N - категория, объектами которой являются натуральные числа 0, 1, 2, ..., с одним морфизмом если в обычном порядке (без морфизмов из я к j в противном случае), и моноидальная структура с моноидальной единицей, заданной 0, и моноидальным умножением, заданным обычным сложением, . потом N моноидальный предзаказ; фактически это тот, который свободно порождается одним объектом 1 и одним морфизмом 0 ≤ 1, где снова 0 - моноидальная единица.
Свойства и связанные с ними понятия
Из трех определяющих условий когерентности следует, что большой класс диаграмм (т.е. диаграмм, морфизмы которых построены с использованием , , , тождества и тензорное произведение) коммутируют: это Mac Lane's "теорема согласованности". Иногда неточно утверждается, что все такие диаграммы коммутируют.
Есть общее понятие моноидный объект в моноидальной категории, которая обобщает обычное понятие моноид из абстрактная алгебра. Обычные моноиды - это в точности моноидные объекты в декартовой моноидальной категории Набор. Далее, любая строго моноидальная категория может рассматриваться как моноидный объект в категории категорий. Кот (снабженный моноидальной структурой, индуцированной декартовым произведением).
Моноидальные функторы - функторы между моноидальными категориями, сохраняющие тензорное произведение, и моноидальные естественные преобразования являются естественными преобразованиями между теми функторами, которые «совместимы» с тензорным произведением.
Каждую моноидальную категорию можно рассматривать как категорию B(∗, ∗) бикатегория B только с одним объектом, обозначенным *.
Категория C обогащенный в моноидальной категории M заменяет понятие набора морфизмов между парами объектов в C с понятием M-объект морфизмов между каждыми двумя объектами в C.
Бесплатная строгая моноидальная категория
Для каждой категории C, то свободный строгая моноидальная категория Σ (C) можно построить следующим образом:
- его объекты - списки (конечные последовательности) А1, ..., Ап объектов C;
- есть стрелки между двумя объектами А1, ..., Ам и B1, ..., Bп только если м = п, и тогда стрелки - это списки (конечные последовательности) стрелок ж1: А1 → B1, ..., жп: Ап → Bп из C;
- тензорное произведение двух объектов А1, ..., Ап и B1, ..., Bм это конкатенация А1, ..., Ап, B1, ..., Bм двух списков, и, аналогично, тензорное произведение двух морфизмов дается конкатенацией списков. Объект идентификации - это пустой список.
Эта операция Σ отображение категории C к Σ (C) можно продолжить до строгого 2-монада на Кот.
Специализации
- Если в моноидальной категории и естественно изоморфны способом, совместимым с условиями когерентности, мы говорим о плетеная моноидальная категория. Если, кроме того, этот естественный изоморфизм является обратным самому себе, мы имеем симметричная моноидальная категория.
- А закрытая моноидальная категория - моноидальная категория, в которой функтор имеет правый смежный, который называется «внутренним Hom-функтором» . Примеры включают декартовы закрытые категории Такие как Набор, категория множеств и компактные закрытые категории Такие как FdVect, категория конечномерных векторных пространств.
- Автономные категории (или же компактные закрытые категории или же жесткие категории) - моноидальные категории, в которых существуют двойники с хорошими свойствами; они абстрагируют идею FdVect.
- Кинжал симметричные моноидальные категории, снабженный дополнительным функтором кинжала, абстрагирующим идею FdHilb, конечномерные гильбертовы пространства. К ним относятся кинжал компактные категории.
- Категории таннакиана - это моноидальные категории, обогащенные над полем, которые очень похожи на категории представлений линейных алгебраических групп.
Смотрите также
Рекомендации
- ^ Баэз, Джон; Останься, Майк (2011). «Физика, топология, логика и вычисления: Розеттский камень». В Coecke, Боб (ред.). Новые структуры для физики. Конспект лекций по физике. 813. Спрингер, Берлин. С. 95–172. arXiv:0903.0340. ISBN 9783642128219. ISSN 0075-8450.
- Хоял, Андре; Улица, Росс (1993). «Плетеные тензорные категории». Успехи в математике 102, 20–78.
- Хоял, Андре; Улица, Росс (1988). "Планарные диаграммы и тензорная алгебра".
- Келли, Дж. Макс (1964). «Об условиях Маклейна для когерентности естественных ассоциативностей, коммутаций и т. Д.» Журнал алгебры 1, 397–402
- Келли, Г. Макс (1982). Основные понятия теории обогащенных категорий (PDF). Серия лекций Лондонского математического общества № 64. Cambridge University Press.
- Мак-Лейн, Сондерс (1963). «Естественная ассоциативность и коммутативность». Исследования Университета Райса 49, 28–46.
- Мак-Лейн, Сондерс (1998), Категории для рабочего математика (2-е изд.). Нью-Йорк: Springer-Verlag.
- Моноидальная категория в nLab