WikiDer > Пятиугольная пирамида

Пятиугольная пирамида
Тип	Джонсон J1 - J2 - J3
Лица	5 треугольники 1 пятиугольник
Края	10
Вершины	6
Конфигурация вершины	5(32.5) (35)
Символ Шлефли	( ) ∨ {5}
Группа симметрии	C5в, [5], (*55)
Группа вращения	C5, [5]+, (55)
Двойной многогранник	себя
Характеристики	выпуклый
Сеть

3D модель пятиугольной пирамиды

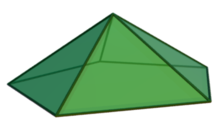
В геометрия, а пятиугольная пирамида это пирамида с пятиугольник фундамент, на котором возведены пять треугольный грани, которые встречаются в точке (вершине). Как и любой пирамида, это само-двойной.

В обычный Пятиугольная пирамида имеет основание, которое представляет собой правильный пятиугольник, а боковые грани равносторонние треугольники. Это один из Твердые тела Джонсона (J₂).

Его можно рассматривать как «крышку» икосаэдр; остальная часть икосаэдра образует гировидная пятиугольная пирамида, J₁₁

В более общем смысле, пятиугольная пирамида с однородной вершиной порядка 2 может быть определена с правильным пятиугольным основанием и 5 сторонами равнобедренного треугольника любой высоты.

Декартовы координаты

Пятиугольную пирамиду можно рассматривать как «крышку» правильный икосаэдр; остальная часть икосаэдра образует гировидная пятиугольная пирамида, J₁₁. От Декартовы координаты икосаэдра декартовы координаты пятиугольной пирамиды с длиной ребра 2 могут быть определены как

${ Displaystyle (1,0, тау), , (- 1,0, тау), , (0, тау, 1), , ( тау, 1,0), ( тау, -1,0), (0, - tau, 1)}$

куда τ (иногда пишется как φ) это Золотое сечение.^[1]

Высота ЧАС, от середины пятиугольной грани до вершины пятиугольной пирамиды с длиной ребра а поэтому может быть вычислено как:

${ displaystyle H = left ({ sqrt { frac {5 - { sqrt {5}}} {10}}} right) a приблизительно 0,52573a.}$^[2]

Его площадь поверхности А можно вычислить как площадь основания пятиугольника плюс площадь одного треугольника, умноженную на пять:

${ displaystyle A = { frac {a ^ {2}} {2}} { sqrt {{ frac {5} {2}} left (10 + { sqrt {5}} + { sqrt { 75 + 30 { sqrt {5}}}} right)}} приблизительно 3.88554 cdot a ^ {2}.}$^[3][2]

Его объем можно рассчитать как:

${ displaystyle V = left ({ frac {5 + { sqrt {5}}} {24}} right) a ^ {3} приблизительно 0,30150a ^ {3}.}$^[3]

Связанные многогранники

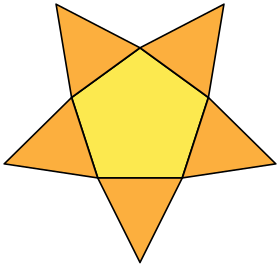
Пентаграмма звездная пирамида имеет то же самое расположение вершин, но подключены к пентаграмма основание:

Правильные пирамиды
Дигональный	Треугольная	Квадрат	Пятиугольный	Шестиугольный	Семиугольный	Восьмиугольный	Эннеагональный	Десятиугольный ...
Неправильный	Обычный	Равносторонний		Равнобедренный

Пятиугольный усеченный представляет собой пятиугольную пирамиду с усеченной вершиной

Вершина икосаэдр это пятиугольная пирамида

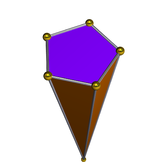
Двойной многогранник

Пятиугольная пирамида топологически самодвойственный многогранник. Длина двух кромок различается из-за полярное возвратно-поступательное движение.

Двойная пятиугольная пирамида	Чистая двойная

Пример

Пятиугольная пирамида (при Математека IME-USP)

Рекомендации

внешняя ссылка

• Эрик В. Вайсштейн, Пятиугольная пирамида (Джонсон солид) в MathWorld.
• Многогранники виртуальной реальности www.georgehart.com: Энциклопедия многогранников ( VRML модель)