WikiDer > Распределение Ирвина – Холла

Распределение Ирвина – Холла

Функция плотности вероятности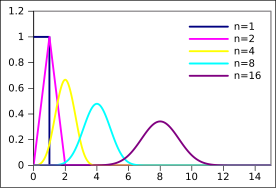
Кумулятивная функция распределения
Параметры	п ∈ N0
Поддерживать	${displaystyle xin [0, n]}$
PDF	${displaystyle {frac {1} {(n-1)!}} sum _ {k = 0} ^ {lfloor xfloor} (- 1) ^ {k} {inom {n} {k}} (xk) ^ { n-1}}$
CDF	${displaystyle {frac {1} {n!}} sum _ {k = 0} ^ {lfloor xfloor} (- 1) ^ {k} {inom {n} {k}} (x-k) ^ {n}}$
Иметь в виду	${displaystyle {frac {n} {2}}}$
Медиана	${displaystyle {frac {n} {2}}}$
Режим	${displaystyle {egin {case} {ext {any value in}} [0,1] & {ext {for}} n = 1 {frac {n} {2}} & {ext {else}} end {case }}}$
Дисперсия	${displaystyle {frac {n} {12}}}$
Асимметрия	0
Бывший. эксцесс	${displaystyle - {frac {6} {5n}}}$
MGF	${displaystyle {left ({frac {mathrm {e} ^ {t} -1} {t}} ight)} ^ {n}}$
CF	${displaystyle {left ({frac {mathrm {e} ^ {it} -1} {it}} ight)} ^ {n}}$

В вероятность и статистика, то Распределение Ирвина – Холла, названный в честь Джозеф Оскар Ирвин и Филип Холл, это распределение вероятностей для случайная переменная определяется как сумма ряда независимый случайные величины, каждая из которых имеет равномерное распределение.^[1] По этой причине он также известен как равномерное распределение суммы.

Поколение псевдослучайные числа имея приблизительно нормальное распределение иногда выполняется путем вычисления суммы ряда псевдослучайных чисел, имеющих равномерное распределение; обычно ради простоты программирования. Изменение масштаба распределения Ирвина – Холла обеспечивает точное распределение генерируемых случайных величин.

Этот дистрибутив иногда путают с Распределение Бейтса, какой иметь в виду (нет сумма) из п независимые случайные величины, равномерно распределенные от 0 до 1.

Определение

Распределение Ирвина – Холла является непрерывным распределение вероятностей на сумму п независимые и одинаково распределенные U(0, 1) случайные переменные:

${displaystyle X = sum _ {k = 1} ^ {n} U_ {k}.}$

В функция плотности вероятности (pdf) дается

${displaystyle f_ {X} (x; n) = {frac {1} {2 (n-1)!}} sum _ {k = 0} ^ {n} (- 1) ^ {k} {n выбрать k } (xk) ^ {n-1} имя оператора {sgn} (xk)}$

где sgn (Икс − k) обозначает функция знака:

${displaystyle operatorname {sgn} (x-k) = {egin {case} -1 & x k.end {case}}}$

Таким образом, PDF-файл является сплайн (кусочно-полиномиальная функция) степени п - 1 по узлам 0, 1, ..., п. Фактически, для Икс между узлами, расположенными в k и k + 1, pdf равен

${displaystyle f_ {X} (x; n) = {frac {1} {(n-1)!}} сумма _ {j = 0} ^ {n-1} a_ {j} (k, n) x ^ {j}}$

где коэффициенты а_j(k,п) можно найти в отношение повторения над k

${displaystyle a_ {j} (k, n) = {egin {case} 1 & k = 0, j = n-1 0 & k = 0, j 0end {case}}}$

Коэффициенты также A188816 в OEIS. Коэффициенты совокупного распределения равны A188668.

В иметь в виду и отклонение находятся п/ 2 и п/ 12 соответственно.

Особые случаи

• За п = 1, Икс следует за равномерное распределение:

${displaystyle f_ {X} (x) = {egin {case} 1 & 0leq xleq 1 0 & {ext {else}} end {cases}}}$

• За п = 2, Икс следует за треугольное распределение:

${displaystyle f_ {X} (x) = {egin {case} x & 0leq xleq 1 2-x & 1leq xleq 2end {case}}}$

• За п = 3,

${displaystyle f_ {X} (x) = {egin {cases} {frac {1} {2}} x ^ {2} & 0leq xleq 1 {frac {1} {2}} (- 2x ^ {2} + 6x-3) & 1leq xleq 2 {frac {1} {2}} (x-3) ^ {2} & 2leq xleq 3end {case}}}$

• За п = 4,

${displaystyle f_ {X} (x) = {egin {cases} {frac {1} {6}} x ^ {3} & 0leq xleq 1 {frac {1} {6}} (- 3x ^ {3} + 12x ^ {2} -12x + 4) & 1leq xleq 2 {frac {1} {6}} (3x ^ {3} -24x ^ {2} + 60x-44) & 2leq xleq 3 {frac {1} { 6}} (- x + 4) ^ {3} & 3leq xleq 4end {case}}}$

• За п = 5,

${displaystyle f_ {X} (x) = {egin {cases} {frac {1} {24}} x ^ {4} & 0leq xleq 1 {frac {1} {24}} (- 4x ^ {4} + 20x ^ {3} -30x ^ {2} + 20x-5) & 1leq xleq 2 {frac {1} {24}} (6x ^ {4} -60x ^ {3} + 210x ^ {2} -300x + 155) & 2leq xleq 3 {frac {1} {24}} (- 4x ^ {4} + 60x ^ {3} -330x ^ {2} + 780x-655) & 3leq xleq 4 {frac {1} {24 }} (x-5) ^ {4} & 4leq xleq 5end {case}}}$

Похожие и родственные дистрибутивы

Распределение Ирвина – Холла аналогично распределению Распределение Бейтса, но по-прежнему с целыми числами в качестве параметра. Расширение до параметров с действительным знаком возможно путем добавления случайной однородной переменной с N - усечение (N) как ширина.

Расширения к распределению Ирвина – Холла.

При использовании Ирвина – Холла для подгонки данных одна проблема заключается в том, что IH не очень гибок, поскольку параметр п должно быть целым числом. Однако вместо суммирования п равномерного равномерного распределения, мы также могли бы добавить, например, U + 0.5U обратиться также к делу п = 1,5 (что дает трапециевидное распределение).

Смотрите также

• Распределение Бейтса
• Нормальное распределение
• Центральная предельная теорема
• Равномерное распределение (непрерывное)
• Треугольное распределение

Примечания

Рекомендации

• Холл, Филипп. (1927) «Распределение средних значений для выборок размера N, взятых из популяции, в которой переменная принимает значения от 0 до 1, все такие значения равновероятны». Биометрика, Vol. 19, № 3/4., С. 240–245. Дои:10.1093 / biomet / 19.3-4.240 JSTOR 2331961
• Ирвин, Дж. (1927) «О частотном распределении средних значений выборок из популяции, имеющей любой закон частоты с конечными моментами, с особым упором на тип II Пирсона». Биометрика, Vol. 19, № 3/4., Стр. 225–239. Дои:10.1093 / biomet / 19.3-4.225 JSTOR 2331960