WikiDer > Преобразование Фурье
В математика, а преобразование Фурье (FT) это математическое преобразование который разлагает функция (часто функция времени, или сигнал) в его составляющую частоты, например, выражение музыкального аккорд с точки зрения объемов и частотности составляющих его нот. Период, термин преобразование Фурье относится как к частотная область представительство и математическая операция который связывает представление частотной области с функцией времени.
Преобразование Фурье функции времени есть комплексная функция частоты, величина которой (абсолютная величина) представляет количество этой частоты, присутствующей в исходной функции, и чья аргумент это фазовый сдвиг основных синусоида в этой частоте. Преобразование Фурье не ограничивается функциями времени, но домен исходной функции обычно называют область времени. Также есть обратное преобразование Фурье который математически синтезирует исходную функцию из ее представления в частотной области, что доказано Теорема обращения Фурье.
А синусоидальный кривая, с пиковой амплитудой (1), от пика до пика (2), RMS (3) и период волны (4).
Линейные операции, выполняемые в одном домене (времени или частоте), имеют соответствующие операции в другом домене, которые иногда легче выполнить. Работа дифференциация во временной области соответствует умножению на частоту,[примечание 1] так что некоторые дифференциальные уравнения легче анализировать в частотной области. Также, свертка во временной области соответствует обычному умножению в частотной области (см. Теорема свертки). После выполнения желаемых операций преобразование результата может быть выполнено обратно во временную область. Гармонический анализ является систематическим изучением взаимосвязи между частотной и временной областями, включая виды функций или операций, которые «проще» в том или ином, и имеет глубокие связи со многими областями современной математики.
Функции, локализованные во временной области, имеют преобразования Фурье, которые распределены по частотной области, и наоборот, явление, известное как принцип неопределенности. В критический аргументом в пользу этого принципа является Функция Гаусса, имеющее большое значение в теория вероятности и статистика а также при изучении физических явлений, проявляющих нормальное распределение (например., распространение). Преобразование Фурье функции Гаусса является другой функцией Гаусса. Жозеф Фурье представил преобразование в своем исследовании теплопередача, где гауссовские функции появляются как решения уравнение теплопроводности.
Преобразование Фурье можно формально определить как неподходящий Интеграл Римана, что делает его интегральное преобразование, хотя это определение не подходит для многих приложений, требующих более сложной теории интеграции.[примечание 2] Например, многие относительно простые приложения используют Дельта-функция Дирака, который формально можно рассматривать как функцию, но для обоснования требуется математически более сложная точка зрения.[примечание 3] Преобразование Фурье также можно обобщить на функции нескольких переменных в евклидовом пространстве, отправив функцию 3-х мерный 'position space' в функцию 3-х мерный импульс (или функция пространства и времени к функции 4-импульс). Эта идея делает пространственное преобразование Фурье очень естественным при изучении волн, а также квантовая механика, где важно иметь возможность представлять волновые решения как функции либо положения, либо импульса, а иногда и того и другого. В общем, функции, к которым применимы методы Фурье, являются комплексными и, возможно, векторнозначный.[примечание 4] Дальнейшее обобщение возможно для функций на группы, которое, помимо исходного преобразования Фурье на ℝ или же ℝп (рассматривается как добавляемые группы), в частности, включает преобразование Фурье с дискретным временем (DTFT, группа = ℤ), дискретное преобразование Фурье (ДПФ, группа = ℤ мод N) и Ряд Фурье или круговое преобразование Фурье (группа = S1, единичная окружность ≈ замкнутый конечный интервал с отождествленными концами). Последний обычно используется для обработки периодические функции. В быстрое преобразование Фурье (БПФ) - это алгоритм вычисления ДПФ.
Определение
Преобразование Фурье функции ж традиционно обозначается , добавив циркумфлекс к символу функции. Есть несколько общие соглашения для определения преобразования Фурье интегрируемый функция .[1][2] Один из них является
| (Уравнение 1) |
для любого настоящий номер ξ.
Причина отрицательного знака в экспоненте заключается в том, что это обычное явление в электротехника к представлятьк сигнал с нулевой начальной фазой и частотой [3][примечание 5] Условное обозначение отрицательного знака приводит к тому, что продукт быть 1 (частота нулевая), когда заставляя интеграл расходиться. В результате Дельта-функция Дирака в , которая является единственной частотной составляющей синусоидальный сигнал
Когда независимая переменная Икс представляет время, переменная преобразования ξ представляет частота (например, если время измеряется в секундах, тогда частота указывается в герц). При подходящих условиях ж определяется через обратное преобразование:
| (Уравнение 2) |
для любого реального числаИкс.
Заявление о том, что ж может быть реконструирован из известен как Теорема обращения Фурье, и впервые был представлен в Фурье Аналитическая теория тепла,[4][5] хотя то, что по современным меркам можно было бы считать доказательством, было дано намного позже.[6][7] Функции ж и часто упоминаются как Интегральная пара Фурье или же Пара преобразований Фурье.[8]
Для других общих соглашений и обозначений, включая использование угловая частота ω вместо частота ξ, видеть Прочие соглашения и Другие обозначения ниже. В Преобразование Фурье на евклидовом пространстве рассматривается отдельно, в котором переменная Икс часто представляет позицию и ξ импульс. Соглашения, выбранные в этой статье, являются гармонический анализ, и характеризуются как уникальные соглашения, так что преобразование Фурье унитарный на L2 и гомоморфизм алгебр из L1 к L∞, без перенормировки меры Лебега.[9]
Существует много других характеристик преобразования Фурье. Например, используется Теорема Стоуна – фон Неймана: преобразование Фурье - единственное унитарное спутник для симплектического и евклидова шредингеровского представлений Группа Гейзенберга.
История
В 1822 г. Жозеф Фурье показал, что некоторые функции можно записать в виде бесконечной суммы гармоник.[10]
Вступление

Одна из причин для преобразования Фурье связана с изучением Ряд Фурье. При изучении рядов Фурье сложные, но периодические функции записываются как сумма простых волн, математически представленных синусы и косинусы. Преобразование Фурье - это расширение ряда Фурье, которое получается, когда период представленной функции удлиняется и приближается к бесконечность.[11]
Благодаря свойствам синуса и косинуса, можно восстановить амплитуду каждой волны в ряду Фурье с помощью интеграла. Во многих случаях желательно использовать Формула Эйлера, в котором говорится, что е2πiθ = cos (2πθ) + я грех (2πθ), чтобы записать ряд Фурье по основным волнам е2πiθ. Это имеет то преимущество, что упрощает многие из используемых формул и обеспечивает формулировку рядов Фурье, которая больше напоминает определение, приведенное в этой статье. Переписываем синусы и косинусы как комплексные экспоненты делает необходимым, чтобы коэффициенты Фурье были комплексными. Обычная интерпретация этого комплексного числа заключается в том, что оно дает как амплитуда (или размер) волны, присутствующей в функции, и фаза (или начальный угол) волны. Эти комплексные экспоненты иногда содержат отрицательные «частоты». Если θ измеряется в секундах, то волны е2πiθ и е−2πiθ оба выполняют один цикл в секунду, но они представляют разные частоты в преобразовании Фурье. Следовательно, частота больше не измеряет количество циклов в единицу времени, но по-прежнему тесно связана.
Существует тесная связь между определением ряда Фурье и преобразованием Фурье для функций ж которые равны нулю вне интервала. Для такой функции мы можем вычислить ее ряд Фурье на любом интервале, включающем точки, где ж не тождественно нулю. Для такой функции также определено преобразование Фурье. По мере увеличения длины интервала, в котором мы вычисляем ряд Фурье, коэффициенты ряда Фурье начинают напоминать преобразование Фурье и сумму ряда Фурье ж начинает напоминать обратное преобразование Фурье. Точнее предположим Т достаточно велик, чтобы интервал [−Т/2, Т/2] содержит интервал, в котором ж не тождественно нулю. Затем пкоэффициент й серии cп дан кем-то:
Сравнивая это с определением преобразования Фурье, следует, что:
поскольку ж (Икс) ноль снаружи [−Т/2, Т/2]. Таким образом, коэффициенты Фурье равны значениям преобразования Фурье, выбранным на сетке шириной 1/Т, умноженное на ширину сетки 1/Т.
При соответствующих условиях ряд Фурье ж будет равно функции ж. Другими словами, ж можно написать:
где последняя сумма - это просто первая сумма, переписанная с использованием определений ξп = п/Т, и Δξ = п + 1/Т − п/Т = 1/Т.
Эта вторая сумма представляет собой Сумма Римана. Позволяя Т → ∞ он будет сходиться к интегралу для обратного преобразования Фурье, как указано выше. При подходящих условиях этот аргумент можно уточнить.[12]
При изучении рядов Фурье числа cп можно рассматривать как "количество" волны, присутствующей в ряду Фурье ж. Точно так же, как показано выше, преобразование Фурье можно рассматривать как функцию, которая измеряет, сколько каждой отдельной частоты присутствует в нашей функции ж, и мы можем рекомбинировать эти волны, используя интеграл (или «непрерывную сумму»), чтобы воспроизвести исходную функцию.
Пример
На следующих рисунках наглядно показано, как преобразование Фурье измеряет, присутствует ли частота в конкретной функции. Изображенная функция ж (т) = cos (6πт) е−πт2 колеблется на 3Гц (если т измеряет секунды) и быстро стремится к 0. (Второй фактор в этом уравнении - это функция конверта который преобразует непрерывную синусоиду в короткий импульс. Его общая форма - Функция Гаусса). Эта функция была специально выбрана для получения реального преобразования Фурье, которое можно легко построить. Первое изображение содержит его график. Чтобы рассчитать мы должны интегрировать е−2πя(3т)ж (т). На втором изображении показан график реальной и мнимой частей этой функции. Действительная часть подынтегрального выражения почти всегда положительна, потому что когда ж (т) отрицательно, действительная часть е−2πя(3т) также отрицательный. Потому что они колеблются с одинаковой скоростью, когда ж (т) положительно, так же как и реальная часть е−2πя(3т). В результате, когда вы интегрируете действительную часть подынтегрального выражения, вы получаете относительно большое число (в данном случае 1/2). С другой стороны, когда вы пытаетесь измерить частоту, которой нет, как в случае, когда мы смотрим на , вы видите, что как реальный, так и мнимый компоненты этой функции быстро меняются между положительными и отрицательными значениями, как показано на третьем изображении. Следовательно, в этом случае подынтегральная функция колеблется достаточно быстро, так что интеграл очень мал, а значение преобразования Фурье для этой частоты почти равно нулю.
Общая ситуация может быть немного более сложной, чем эта, но по духу преобразование Фурье измеряет, сколько отдельной частоты присутствует в функции. ж (т).
Свойства преобразования Фурье
Здесь мы предполагаем ж (Икс), грамм(Икс) и час(Икс) находятся интегрируемые функции: Измеримый по Лебегу на реальной линии, удовлетворяющей:
Обозначим преобразования Фурье этих функций как f̂ (ξ), грамм(ξ) и час(ξ) соответственно.
Основные свойства
Преобразование Фурье имеет следующие основные свойства:[13]
Линейность
- Для любого сложные числа а и б, если час(Икс) = аф (Икс) + bg(Икс), тогда час(ξ) = а · f̂ (ξ) + б · грамм(ξ).
Перевод / сдвиг во времени

- Для любого настоящий номер Икс0, если час(Икс) = ж (Икс − Икс0), тогда час(ξ) = е−2πix0ξ f̂ (ξ).
Модуляция / частотный сдвиг
- Для любого настоящий номер ξ0, если час(Икс) = е2πixξ0 ж (Икс), тогда час(ξ) = f̂ (ξ − ξ0).
Масштабирование времени
- Для ненулевого настоящий номер а, если час(Икс) = ж (топор), тогда
- Дело а = −1 приводит к обращение времени свойство, в котором говорится: если час(Икс) = ж (−Икс), тогда час(ξ) = f̂ (−ξ).
Конъюгация
- Если час(Икс) = ж (Икс), тогда
- В частности, если ж реально, то есть состояние реальности
- то есть, f̂ это Эрмитова функция. И если ж чисто мнимое, то
Реальная и мнимая часть времени
- Если , тогда .
- Если , тогда .
Интеграция
- Подстановка ξ = 0 в определении получаем
- То есть оценка преобразования Фурье в начале координат (ξ = 0) равно интегралу от ж по всей своей области.
Обратимость и периодичность
При подходящих условиях на функции ж, его можно восстановить из его преобразования Фурье . Действительно, обозначая оператор преобразования Фурье как F, так F( ж ) := f̂, то для подходящих функций двойное применение преобразования Фурье просто переворачивает функцию: F2( ж )(Икс) = ж (−Икс), что можно интерпретировать как «время обращения вспять». Поскольку время обращения двухпериодично, применение этого дважды дает F4( ж ) = ж, поэтому оператор преобразования Фурье является четырехпериодическим, и аналогичным образом обратное преобразование Фурье может быть получено путем трехкратного применения преобразования Фурье: F3( f̂ ) = ж. В частности, преобразование Фурье обратимо (при подходящих условиях).
Точнее, определяя оператор четности п что переворачивает время, п[ ж ] : т ↦ ж (−т):
Эти равенства операторов требуют тщательного определения пространства рассматриваемых функций, определяя равенство функций (равенство в каждой точке? Равенство почти всюду?) и определение равенства операторов, то есть определение топологии на рассматриваемом функциональном пространстве и пространстве операторов. Это верно не для всех функций, но справедливо при различных условиях, которые являются содержанием различных форм Теорема обращения Фурье.
Эта четырехкратная периодичность преобразования Фурье аналогична повороту плоскости на 90 °, особенно потому, что двукратная итерация дает разворот, и фактически эта аналогия может быть точной. Хотя преобразование Фурье можно просто интерпретировать как переключение временной области и частотной области, с обратным преобразованием Фурье, переключающей их обратно, более геометрически его можно интерпретировать как поворот на 90 ° в частотно-временной диапазон (рассматривая время как Иксось и частота как у-ось), а преобразование Фурье обобщается на дробное преобразование Фурье, который включает повороты на другие углы. В дальнейшем это можно обобщить на линейные канонические преобразования, который можно представить как действие специальная линейная группа SL2(ℝ) на частотно-временной плоскости с сохранением симплектической формы, соответствующей принцип неопределенности, ниже. Этот подход особенно изучен в обработка сигналов, под частотно-временной анализ.
Единицы и двойственность
В математике часто не думают, что какие-либо единицы связаны с двумя переменными. т и ξ. Но в физических приложениях ξ должны иметь единицы, обратные единицам т. Например, если т измеряется в секундах, ξдолжны быть циклами в секунду, чтобы приведенные здесь формулы были действительными. Если масштаб т изменено и т измеряется в единицах 2π секунд, затем либо ξ должен быть в так называемом "угловая частота", или нужно вставить некоторый постоянный масштабный коэффициент в некоторые формулы. Если т измеряется в единицах длины, то ξ должен иметь обратную длину, например, волновые числа. То есть есть две копии реальной линии: одна измеряется в одном наборе единиц, где т диапазоны, а другой - в единицах, обратных единицам т, а это диапазон ξ. Итак, это две разные копии настоящей линии, и их нельзя отождествить друг с другом. Следовательно, преобразование Фурье переходит из одного пространства функций в другое пространство функций: функции, которые имеют другую область определения.
В целом, ξ всегда следует воспринимать как линейная форма на пространстве тs, что означает, что вторая действительная линия - это двойное пространство первой реальной линии. См. Статью о линейная алгебра для более формального объяснения и более подробной информации. Эта точка зрения становится существенной при обобщении преобразования Фурье на общие группы симметрии, включая случай рядов Фурье.
Что не существует одного предпочтительного способа (часто говорят «не канонический») для сравнения двух копий реальной линии, которые участвуют в преобразовании Фурье - фиксация единиц на одной строке не приводит к изменению масштаба единиц измерения. другая строка - причина множества конкурирующих соглашений по определению преобразования Фурье. Различные определения, полученные в результате различного выбора единиц, различаются разными константами. Если единицы т в секундах, но единицы измерения ξ находятся в угловой частоте, то переменная угловой частоты часто обозначается той или иной греческой буквой, например, ω = 2πξ довольно часто. Таким образом (написание Икс1 для альтернативного определения и Икс для определения, принятого в этой статье)
как и раньше, но соответствующая альтернативная формула обращения должна быть
Чтобы иметь что-то, связанное с угловой частотой, но с большей симметрией между преобразованием Фурье и формулой обращения, очень часто можно увидеть еще одно альтернативное определение преобразования Фурье с коэффициентом √2π, таким образом
и соответствующая формула обращения тогда должна быть
В некоторых необычных условных обозначениях, таких как используемые командой FourierTransform Язык Wolfram Language, преобразование Фурье имеет я в экспоненте вместо −я, и наоборот для формулы обращения. Многие тождества, включающие преобразование Фурье, остаются действительными в этих соглашениях при условии, что все термины, которые явно включают я заменить его на −я.
Например, в теории вероятностей характеристическая функция ϕ функции плотности вероятности ж случайной величины Икс непрерывного типа определяется без знака минус в экспоненте, и поскольку единицы Икс игнорируются, нет 2π либо:
(В теории вероятностей и в математической статистике предпочтительнее использовать преобразование Фурье-Стилтьеса, потому что так много случайных величин не имеют непрерывного типа и не обладают функцией плотности, и нужно рассматривать не функции, а распределения, т.е. меры, содержащие "атомы".)
С более высокой точки зрения группа персонажей, что является гораздо более абстрактным, все эти произвольные выборы исчезают, как будет объяснено в следующем разделе этой статьи, в котором рассматривается понятие преобразования Фурье функции на локально компактная абелева группа.
Равномерная непрерывность и лемма Римана – Лебега

Преобразование Фурье может быть определено в некоторых случаях для неинтегрируемых функций, но преобразования Фурье интегрируемых функций обладают несколькими сильными свойствами.
Преобразование Фурье f̂ любой интегрируемой функции ж является равномерно непрерывный и[14]
Посредством Лемма Римана – Лебега.,[15]
Тем не мение, не обязательно должны быть интегрируемыми. Например, преобразование Фурье прямоугольная функция, интегрируемая, является функция sinc, который не Интегрируемый по Лебегу, потому что это несобственные интегралы вести себя аналогично переменный гармонический ряд, сходясь к сумме, не будучи абсолютно сходящийся.
Как правило, невозможно написать обратное преобразование как Интеграл Лебега. Однако когда оба ж и интегрируемы, обратное равенство
держит почти всюду. То есть преобразование Фурье имеет вид инъективный на L1(ℝ). (Но если ж непрерывна, то равенство выполняется для любого Икс.)
Теорема Планшереля и теорема Парсеваля
Позволять ж (Икс) и грамм(Икс) быть интегрируемым, и пусть f̂ (ξ) и грамм(ξ) - их преобразования Фурье. Если ж (Икс) и грамм(Икс) являются также интегрируемый с квадратом, то формула Парсеваля следует:[16]
где черта обозначает комплексное сопряжение.
В Теорема Планшереля, что следует из вышеизложенного, утверждает, что[17]
Теорема Планшереля позволяет распространить преобразование Фурье с помощью аргумента непрерывности до унитарный оператор на L2(ℝ). На L1(ℝ) ∩ L2(ℝ), это расширение согласуется с исходным преобразованием Фурье, определенным на L1(ℝ), расширяя таким образом область преобразования Фурье до L1(ℝ) + L2(ℝ) (и, следовательно, Lп(ℝ) за 1 ≤ п ≤ 2). Теорема Планшереля имеет научную интерпретацию, согласно которой преобразование Фурье сохраняет энергия от первоначального количества. Терминология этих формул не совсем стандартизирована. Теорема Парсеваля была доказана только для рядов Фурье и впервые была доказана Ляпуновым. Но формула Парсеваля имеет смысл и для преобразования Фурье, и поэтому, хотя в контексте преобразования Фурье она была доказана Планшерелем, ее по-прежнему часто называют формулой Парсеваля, соотношением Парсеваля или даже теоремой Парсеваля.
Видеть Понтрягинская двойственность для общей формулировки этого понятия в контексте локально компактных абелевых групп.
Формула суммирования Пуассона
Формула суммирования Пуассона (PSF) - это уравнение, которое связывает Ряд Фурье коэффициенты периодическое суммирование функции к значениям непрерывного преобразования Фурье функции. Формула суммирования Пуассона говорит, что для достаточно регулярных функций ж,
Он имеет множество полезных форм, которые являются производными от основной путем применения свойств масштабирования и сдвига во времени преобразования Фурье. Формула имеет применение в инженерии, физике и теория чисел. Частотная область, двойственная стандартной формуле суммирования Пуассона, также называется преобразование Фурье с дискретным временем.
Суммирование Пуассона обычно связано с физикой периодических сред, таких как теплопроводность по окружности. Фундаментальное решение уравнения теплопроводности на окружности называется тета-функция. Он используется в теория чисел чтобы доказать свойства преобразования тета-функций, которые оказываются разновидностью модульная форма, и это связано в более общем плане с теорией автоморфные формы где он появляется на одной стороне Формула следа Сельберга.
Дифференциация
Предполагать ж (Икс) является абсолютно непрерывной дифференцируемой функцией, и обе ж и его производная f ′ интегрируемы. Тогда преобразование Фурье производной дается выражением
В более общем смысле преобразование Фурье пth производная ж(п) дан кем-то
Применяя преобразование Фурье и используя эти формулы, некоторые обыкновенные дифференциальные уравнения можно преобразовать в алгебраические уравнения, которые намного проще решить. Эти формулы также дают начало практическому правилу "ж (Икс) гладкий если и только если f̂ (ξ) быстро падает до 0 для |ξ| → ∞. "Используя аналогичные правила для обратного преобразования Фурье, можно также сказать"ж (Икс) быстро падает до 0 для |Икс| → ∞ если и только если f̂ (ξ) гладко ".
Теорема свертки
Преобразование Фурье переводит между свертка и умножение функций. Если ж (Икс) и грамм(Икс) - интегрируемые функции с преобразованиями Фурье f̂ (ξ) и грамм(ξ) соответственно, то преобразование Фурье свертки дается произведением преобразований Фурье f̂ (ξ) и грамм(ξ) (согласно другим соглашениям для определения преобразования Фурье может появиться постоянный множитель).
Это означает, что если:
куда ∗ обозначает операцию свертки, тогда:
В теория линейных инвариантных во времени (LTI) систем, принято интерпретировать грамм(Икс) как импульсивный ответ системы LTI с вводом ж (Икс) и вывод час(Икс), так как замена единичный импульс за ж (Икс) дает час(Икс) = грамм(Икс). В этом случае, грамм(ξ) представляет частотный отклик системы.
Наоборот, если ж (Икс) можно разложить как произведение двух интегрируемых с квадратом функций п(Икс) и q(Икс), то преобразование Фурье ж (Икс) дается сверткой соответствующих преобразований Фурье п(ξ) и q̂(ξ).
Теорема взаимной корреляции
Аналогичным образом можно показать, что если час(Икс) это взаимная корреляция из ж (Икс) и грамм(Икс):
то преобразование Фурье час(Икс) является:
В частном случае автокорреляция функции ж (Икс) является:
для которого
Собственные функции
Один важный выбор ортонормированного базиса для L2(ℝ) дается функциями Эрмита
куда Онп(Икс) являются "вероятностными" Полиномы Эрмита, определяется как
Согласно этому соглашению для преобразования Фурье, мы имеем, что
- .
Другими словами, функции Эрмита образуют полную ортонормированный система собственные функции для преобразования Фурье на L2(ℝ).[13] Однако такой выбор собственных функций не уникален. Всего четыре разных собственные значения преобразования Фурье (± 1 и ±я), и любая линейная комбинация собственных функций с одним и тем же собственным значением дает другую собственную функцию. Вследствие этого можно разложить L2(ℝ) как прямая сумма четырех пробелов ЧАС0, ЧАС1, ЧАС2, и ЧАС3 где преобразование Фурье действует на Онk просто умножением на яk.
Поскольку полный набор функций Эрмита обеспечивает разрешение тождества, преобразование Фурье может быть представлено такой суммой членов, взвешенных указанными выше собственными значениями, и эти суммы могут быть явно просуммированы. Этот подход к определению преобразования Фурье был впервые применен Норберт Винер.[18] Помимо других свойств, функции Эрмита экспоненциально быстро убывают как в частотной, так и во временной областях, и поэтому они используются для определения обобщения преобразования Фурье, а именно: дробное преобразование Фурье используется в частотно-временном анализе.[19] В физика, это преобразование было введено Эдвард Кондон.[20]
Связь с группой Гейзенберга
В Группа Гейзенберга это определенный группа из унитарные операторы на Гильбертово пространство L2(ℝ) комплекснозначных функций, интегрируемых с квадратом ж на реальной линии, сгенерированной переводами (Ту ж )(Икс) = ж (Икс + у) и умножение на е2πixξ, (Mξ ж )(Икс) = е2πixξ ж (Икс). Эти операторы не коммутируют, так как их (групповой) коммутатор
умножение на константу (не зависящую от Икс) е2πiyξ ∈ U(1) (в круговая группа комплексных чисел единичного модуля). Как абстрактная группа, группа Гейзенберга представляет собой трехмерную Группа Ли троек (Икс, ξ, z) ∈ ℝ2 × U(1), с групповым законом
Обозначим группу Гейзенберга через ЧАС1. Приведенная выше процедура описывает не только структуру группы, но и стандартную унитарное представительство из ЧАС1 на гильбертовом пространстве, которое мы обозначим через ρ : ЧАС1 → B(L2(ℝ)). Определим линейный автоморфизм ℝ2 к
так что J2 = −я. Этот J продолжается до единственного автоморфизма ЧАС1:
Согласно Теорема Стоуна – фон Неймана, унитарные представления ρ и ρ ∘ j унитарно эквивалентны, поэтому существует уникальный сплетник W ∈ U(L2(ℝ)) такой, что
Этот оператор W - преобразование Фурье.
Многие стандартные свойства преобразования Фурье являются непосредственными следствиями этой более общей структуры.[21] Например, квадрат преобразования Фурье, W2, является спутником, связанным с J2 = −я, и поэтому у нас есть (W2ж )(Икс) = ж (−Икс) является отражением исходной функции ж.
Комплексный домен
В интеграл для преобразования Фурье
можно изучить для сложный значения его аргумента ξ. В зависимости от свойств ж, он может вообще не сходиться с реальной оси или может сходиться к сложный аналитическая функция для всех значений ξ = σ + я, или что-то среднее.[22]
В Теорема Пэли – Винера. Говорит, что ж гладкая (т.е. п-раз дифференцируемые для всех положительных целых чисел п) и имеет компактную опору тогда и только тогда, когда f̂ (σ + я) это голоморфная функция для которого существует постоянный а > 0 такой, что для любого целое число п ≥ 0,
для некоторой постоянной C. (В этом случае, ж поддерживается на [−а, а].) Это можно выразить, сказав, что f̂ является вся функция который быстро уменьшается в σ (для фиксированных τ) и экспоненциального роста τ (равномерно в σ).[23]
(Если ж не гладко, а только L2, утверждение остается в силе при условии п = 0.[24]) Пространство таких функций от комплексная переменная называется пространством Пэли — Винера. Эта теорема была обобщена на полупростые Группы Ли.[25]
Если ж поддерживается на полуоси т ≥ 0, тогда ж считается "причинным", потому что функция импульсного отклика физически реализуемого фильтр должен обладать этим свойством, так как никакое следствие не может предшествовать его причине. Палей и Винер показал, что тогда f̂ распространяется на голоморфная функция на комплексной нижней полуплоскости τ < 0 который стремится к нулю при τ уходит в бесконечность.[26] Обратное неверно, и неизвестно, как охарактеризовать преобразование Фурье причинной функции.[27]
Преобразование Лапласа
Преобразование Фурье f̂ (ξ) относится к Преобразование Лапласа F(s), который также используется для решения дифференциальные уравнения и анализ фильтры.
Может случиться так, что функция ж для которых интеграл Фурье вообще не сходится на действительной оси, тем не менее имеет комплексное преобразование Фурье, определенное в некоторой области комплексная плоскость.
Например, если ж (т) имеет экспоненциальный рост, т.е.
для некоторых констант C, а ≥ 0, тогда[28]
сходится для всех 2πτ < −а, это двустороннее преобразование Лапласа из ж.
Более обычная версия («односторонняя») преобразования Лапласа - это
Если ж тоже причинно, тогда
Таким образом, расширение преобразования Фурье на комплексную область означает, что оно включает преобразование Лапласа как частный случай - случай причинных функций - но с заменой переменной s = 2πiξ.
Инверсия
Если f̂ является комплексно аналитическим для а ≤ τ ≤ б, тогда
к Интегральная теорема Коши. Следовательно, формула обращения Фурье может использовать интегрирование по разным линиям, параллельным действительной оси.[29]
Теорема: если ж (т) = 0 за т < 0, и |ж (т)| < Ceа|т| для некоторых констант C, а > 0, тогда
для любого τ < −а/2π.
Из этой теоремы следует Формула обращения Меллина для преобразования Лапласа[28]
для любого б > а, куда F(s) преобразование Лапласа ж (т).
Гипотезы можно ослабить, как в результатах Карлемана и Ханта, до ж (т) е−в существование L1, при условии, что ж имеет ограниченную вариацию в замкнутой окрестности точки т (ср. Теорема Дирихле-Дини), значение ж в т считается среднее арифметическое левого и правого пределов и при условии, что интегралы взяты в смысле главных значений Коши.[30]
L2 также доступны версии этих формул обращения.[31]
Преобразование Фурье на евклидовом пространстве
Преобразование Фурье можно определить в любом произвольном количестве измерений. п. Как и в случае с одномерным случаем, существует множество соглашений. Для интегрируемой функции ж (Икс), в этой статье используется определение:
куда Икс и ξ находятся п-размерный векторов, и Икс · ξ это скалярное произведение векторов. В качестве альтернативы, ξ можно рассматривать как принадлежащие к двойное векторное пространство , и в этом случае скалярное произведение становится сокращение из Икс и ξ, обычно пишется как ⟨Икс, ξ⟩.
Все основные свойства, перечисленные выше, сохраняются для п-мерное преобразование Фурье, как и теорема Планшереля и Парсеваля. Когда функция интегрируема, преобразование Фурье по-прежнему равномерно непрерывно и Лемма Римана – Лебега. держит.[15]
Принцип неопределенности
Вообще говоря, более концентрированные ж (Икс) есть, чем более распространено его преобразование Фурье f̂ (ξ) должно быть. В частности, свойство масштабирования преобразования Фурье можно рассматривать как выражение: если мы сжимаем функцию в Икс, его преобразование Фурье простирается в ξ. Невозможно произвольно сконцентрировать одновременно функцию и ее преобразование Фурье.
Компромисс между сжатием функции и ее преобразованием Фурье можно формализовать в виде принцип неопределенности рассматривая функцию и ее преобразование Фурье как сопряженные переменные с уважением к симплектическая форма на частотно-временной диапазон: с точки зрения линейное каноническое преобразование, преобразование Фурье представляет собой поворот на 90 ° в частотно-временной области и сохраняет симплектическая форма.
Предполагать ж (Икс) является интегрируемым и интегрируемый с квадратом функция. Без ограничения общности предположим, что ж (Икс) нормализовано:
Это следует из Теорема Планшереля который f̂ (ξ) также нормализуется.
Распространение вокруг Икс = 0 может быть измерено разброс около нуля[32] определяется
С точки зрения вероятности это второй момент из |ж (Икс)|2 около нуля.
Принцип неопределенности гласит, что если ж (Икс) абсолютно непрерывна, а функции Икс·ж (Икс) и ж ′(Икс) квадратично интегрируемы, то[13]
- .
Равенство достигается только в случае
куда σ > 0 произвольно и C1 = 4√2/√σ так что ж является L2-нормализованный.[13] Другими словами, где ж является (нормализованным) Функция Гаусса с отклонением σ2с центром в нуле, а его преобразование Фурье является гауссовой функцией с дисперсией σ−2.
Фактически это неравенство означает, что:
для любого Икс0, ξ0 ∈ ℝ.[12]
В квантовая механика, то импульс и положение волновые функции пары преобразований Фурье с точностью до множителя Постоянная планка. При правильном учете этой константы указанное выше неравенство становится утверждением Принцип неопределенности Гейзенберга.[33]
Более сильный принцип неопределенности - это Принцип неопределенности Хиршмана, что выражается как:
куда ЧАС(п) это дифференциальная энтропия из функция плотности вероятности п(Икс):
где логарифмы могут быть в любом непротиворечивом основании. Равенство достигается для гауссиана, как и в предыдущем случае.
Преобразования синуса и косинуса
В первоначальной формулировке преобразования Фурье использовались не комплексные числа, а синусы и косинусы. Статистики и другие до сих пор используют эту форму. Абсолютно интегрируемая функция ж для которых имеет место инверсия Фурье, можно разложить на истинные частоты (избегая отрицательных частот, которые иногда трудно интерпретировать физически.[34]) λ к
Это называется разложением в виде тригонометрического интеграла или разложением интеграла Фурье. Коэффициентные функции а и б можно найти с помощью вариантов косинусного преобразования Фурье и синус-преобразования Фурье (нормализации, опять же, не стандартизированы):
и
В более ранней литературе упоминаются две функции преобразования, косинусное преобразование Фурье, а, и синусоидальное преобразование Фурье, б.
Функция ж может быть восстановлен из преобразования синуса и косинуса, используя
вместе с тригонометрическими тождествами. Это называется интегральной формулой Фурье.[28][35][36][37]
Сферические гармоники
Пусть набор однородный гармонический многочлены степени k на ℝп обозначать Аk. Набор Аk состоит из сплошные сферические гармоники степени k. Сплошные сферические гармоники в высших измерениях играют ту же роль, что и полиномы Эрмита в размерности один. В частности, если ж (Икс) = е−π |Икс|2п(Икс) для некоторых п(Икс) в Аk, тогда f̂ (ξ) = я−k ж (ξ). Пусть набор ЧАСk быть закрытием в L2(ℝп) линейных комбинаций функций вида ж (|Икс|)п(Икс) куда п(Икс) в Аk. Космос L2(ℝп) тогда является прямой суммой пространств ЧАСk и преобразование Фурье отображает каждое пространство ЧАСk самому себе и можно охарактеризовать действие преобразования Фурье на каждом пространстве ЧАСk.[15]
Позволять ж (Икс) = ж0(|Икс|)п(Икс) (с п(Икс) в Аk), тогда
куда
Здесь Jп + 2k − 2/2 обозначает Функция Бесселя первого вида с заказом п + 2k − 2/2. Когда k = 0 это дает полезную формулу для преобразования Фурье радиальной функции.[38] По сути, это Преобразование Ганкеля. Более того, существует простая рекурсия, связывающая случаи п + 2 и п[39] позволяющий вычислить, например, трехмерное преобразование Фурье радиальной функции из одномерной.
Проблемы с ограничениями
В высших измерениях становится интересно изучать проблемы с ограничениями для преобразования Фурье. Преобразование Фурье интегрируемой функции является непрерывным и определено ограничение этой функции на любое множество. Но для функции, интегрируемой с квадратом, преобразование Фурье могло бы быть общим учебный класс квадратично интегрируемых функций. Таким образом, ограничение преобразования Фурье L2(ℝп) функция не может быть определена на наборах меры 0. Это все еще активная область исследования, чтобы понять проблемы ограничений в Lп за 1 < п < 2. Удивительно, но в некоторых случаях можно определить ограничение преобразования Фурье на множество S, при условии S имеет ненулевую кривизну. Случай, когда S это единичная сфера в ℝп представляет особый интерес. В этом случае Tomas–Stein Теорема ограничения утверждает, что ограничение преобразования Фурье на единичную сферу в ℝп является ограниченным оператором на Lп при условии 1 ≤ п ≤ 2п + 2/п + 3.
Одно заметное различие между преобразованием Фурье в одномерном измерении и в более высоком измерении касается оператора частичной суммы. Рассмотрим увеличивающийся набор измеримых множеств Eр проиндексировано р ∈ (0,∞): например, шары радиуса р с центром в начале координат, или кубики стороны 2р. Для заданной интегрируемой функции жрассмотрим функцию жр определяется:
Предположим дополнительно, что ж ∈ Lп(ℝп). За п = 1 и 1 < п < ∞, если взять Eр = (−р, р), тогда жр сходится к ж в Lп в качестве р стремится к бесконечности в силу ограниченности Преобразование Гильберта. Наивно можно надеяться, что то же самое верно и для п > 1. В случае, если Eр принимается куб с длиной стороны р, то сходимость сохраняется. Еще один естественный кандидат - евклидов шар. Eр = {ξ : |ξ| < р}. Чтобы этот оператор частичной суммы сходился, необходимо, чтобы множитель для единичного шара был ограничен в Lп(ℝп). За п ≥ 2 это знаменитая теорема Чарльз Фефферман что множитель для единичного шара никогда не ограничен, если п = 2.[18] Фактически, когда п ≠ 2, это показывает, что не только жр не сходиться к ж в Lп, но для некоторых функций ж ∈ Lп(ℝп), жр это даже не элемент Lп.
Преобразование Фурье на функциональных пространствах
На Lп пробелы
На L1
Определение преобразования Фурье интегральной формулой
справедливо для интегрируемых по Лебегу функций ж; то есть, ж ∈ L1(ℝп).
Преобразование Фурье F : L1(ℝп) → L∞(ℝп) это ограниченный оператор. Это следует из наблюдения, что
что показывает, что его норма оператора ограничено 1. Действительно, оно равно 1, что видно, например, из преобразование функции rect. Образ L1 является подмножеством пространства C0(ℝп) непрерывных функций, стремящихся к нулю на бесконечности ( Лемма Римана – Лебега.), хотя это не все пространство. Действительно, простой характеристики изображения не существует.
На L2
Поскольку гладкие функции с компактным носителем интегрируемы и плотны в L2(ℝп), то Теорема Планшереля позволяет распространить определение преобразования Фурье на общие функции в L2(ℝп) аргументами преемственности. Преобразование Фурье в L2(ℝп) больше не дается обычным интегралом Лебега, хотя его можно вычислить с помощью несобственный интеграл, здесь имеется в виду, что для L2 функция ж,
где предел взят в L2 смысл. (В более общем смысле, вы можете взять последовательность функций, находящихся на пересечении L1 и L2 и это сходится к ж в L2-нормы и определим преобразование Фурье ж как L2 -предел преобразований Фурье этих функций.[40])
Многие свойства преобразования Фурье в L1 переносить на L2, подходящим ограничивающим аргументом.
Более того, F : L2(ℝп) → L2(ℝп) это унитарный оператор.[41] Чтобы оператор был унитарным, достаточно показать, что он биективен и сохраняет скалярное произведение, поэтому в этом случае они следуют из теоремы об обращении Фурье в сочетании с тем фактом, что для любого ж, грамм ∈ L2(ℝп) у нас есть
В частности, изображение L2(ℝп) само находится под преобразованием Фурье.
На других Lп
Определение преобразования Фурье можно распространить на функции из Lп(ℝп) за 1 ≤ п ≤ 2 путем разложения таких функций на часть толстого хвоста в L2 плюс часть толстого тела в L1. В каждом из этих пространств преобразование Фурье функции из Lп(ℝп) в Lq(ℝп), куда q = п/п − 1 гёльдеровское сопряжение п (посредством Неравенство Хаусдорфа – Юнга.). Однако кроме п = 2, изображение трудно охарактеризовать. Дальнейшие расширения становятся более техническими. Преобразование Фурье функций в Lп для диапазона 2 < п < ∞ требует изучения распределений.[14] Фактически, можно показать, что в Lп с п > 2 так что преобразование Фурье не определяется как функция.[15]
Закаленные дистрибутивы
Можно было бы рассмотреть возможность расширения области преобразования Фурье с L1 + L2 С учетом обобщенные функции, или дистрибутивы. Распространение на ℝп - линейный непрерывный функционал на пространстве Cc(ℝп) гладких функций с компактным носителем и подходящей топологии. Стратегия состоит в том, чтобы рассмотреть действие преобразования Фурье на Cc(ℝп) и перейти к распределениям по двойственности. Препятствием к этому является то, что преобразование Фурье не отображает Cc(ℝп) к Cc(ℝп). Фактически преобразование Фурье элемента в Cc(ℝп) не может исчезнуть на открытой площадке; см. выше обсуждение принципа неопределенности. Правильное пространство здесь - это немного большее пространство Функции Шварца. Преобразование Фурье является автоморфизмом на пространстве Шварца как топологическом векторном пространстве и, таким образом, индуцирует автоморфизм на двойственном ему пространстве умеренных распределений.[15] Умеренные распределения включают в себя все упомянутые выше интегрируемые функции, а также хорошо настроенные функции полиномиального роста и распределения компактного носителя.
Для определения преобразования Фурье умеренного распределения пусть ж и грамм - интегрируемые функции, и пусть f̂ и грамм - их преобразования Фурье соответственно. Тогда преобразование Фурье подчиняется следующей формуле умножения:[15]
Каждая интегрируемая функция ж определяет (индуцирует) распределение Тж отношением
для всех функций Шварца φ. Поэтому имеет смысл определить преобразование Фурье T̂ж из Тж к
для всех функций Шварца φ. Распространение этого на все умеренные дистрибутивы Т дает общее определение преобразования Фурье.
Распределения можно дифференцировать, и упомянутая выше совместимость преобразования Фурье с дифференцированием и сверткой остается верной для умеренных распределений.
Обобщения
Преобразование Фурье – Стилтьеса
Преобразование Фурье конечной борелевской меры μ на ℝп дан кем-то:[42]
Это преобразование по-прежнему обладает многими свойствами преобразования Фурье интегрируемых функций. Одно заметное отличие состоит в том, что Лемма Римана – Лебега. не по мерам.[14] В случае, если dμ = ж (Икс) dx, то приведенная выше формула сводится к обычному определению преобразования Фурье ж. В случае, если μ это распределение вероятностей, связанное со случайной величиной Икспреобразование Фурье – Стилтьеса тесно связано с характеристическая функция, но типичные соглашения в теории вероятностей принимают еixξ вместо е−2πixξ.[13] В случае, когда в раздаче функция плотности вероятности это определение сводится к преобразованию Фурье, применяемому к функции плотности вероятности, опять же с другим выбором констант.
Преобразование Фурье можно использовать для характеристики мер. Теорема Бохнера характеризует, какие функции могут возникать при преобразовании Фурье – Стилтьеса положительной меры на окружности.[14]
Кроме того, Дельта-функция Дирака, хотя и не функция, но является конечным Мера Бореля. Его преобразование Фурье является постоянной функцией (конкретное значение которой зависит от формы используемого преобразования Фурье).
Локально компактные абелевы группы
Преобразование Фурье можно обобщить на любую локально компактную абелеву группу. Локально компактная абелева группа - это абелева группа это в то же время локально компактный Хаусдорфово топологическое пространство так что групповая операция будет непрерывной. Если грамм является локально компактной абелевой группой, она имеет трансляционно-инвариантную меру μ, называется Мера Хаара. Для локально компактной абелевой группы грамм, множество неприводимых, т. е. одномерных, унитарных представлений называется его символы. Благодаря своей естественной групповой структуре и топологии поточечной сходимости множество характеров ГРАММ является локально компактной абелевой группой, называемой Понтрягин дуальный из грамм. Для функции ж в L1(грамм), его преобразование Фурье определяется формулой[14]
В этом случае верна лемма Римана – Лебега; f̂ (ξ) - функция, исчезающая на бесконечности на ГРАММ.
Преобразование Фурье на Т= R / Z является примером; здесь Т является локально компактной абелевой группой, а мера Хаара μ на Т можно рассматривать как меру Лебега на [0,1). Рассмотрим представление Т на комплексной плоскости C это одномерное комплексное векторное пространство. Есть группа представлений (которые неприводимы, так как C 1-тусклый) куда за .
Характер такого представления, то есть след для каждого и , является сам. В случае представления конечной группы таблица характеров группы грамм - строки векторов, каждая из которых является характером одного неприводимого представления грамм, и эти векторы образуют ортонормированный базис пространства функций классов, отображаемых из грамм к C по лемме Шура. Теперь группа Т больше не является конечным, но все еще компактным, и он сохраняет ортонормированность таблицы символов. Каждая строка таблицы - это функция из и внутренний продукт между двумя функциями класса (все функции являются функциями класса, поскольку Т абелева) ж, определяется как с нормирующим фактором Последовательность является ортонормированным базисом пространства функций классов
Для любого представительства V конечной группы грамм, можно выразить как промежуток ( детали грамм), с.т. . Аналогично для и , . Двойственный Понтрягин является и для , его преобразование Фурье для .
Преобразование Гельфанда
Преобразование Фурье также является частным случаем Преобразование Гельфанда. В данном конкретном контексте это тесно связано с картой двойственности Понтрягина, определенной выше.
Учитывая абелевский локально компактный Хаусдорф топологическая группа грамм, как и раньше, мы рассматриваем пространство L1(грамм), определенный с помощью меры Хаара. С сверткой как умножением, L1(грамм) абелева Банахова алгебра. Он также имеет инволюция * предоставлено
Взяв завершение по максимально возможному C*-norm дает обволакивающий C*-алгебра, называемая группой C*-алгебра C*(грамм) из грамм. (Любой C*-норма на L1(грамм) ограничен L1 норма, следовательно, их супремум существует.)
Учитывая любой абелев C*-алгебра А, преобразование Гельфанда дает изоморфизм между А и C0(А^), куда А^ - мультипликативные линейные функционалы, т. е. одномерные представления, на А со слабой * топологией. Карта просто дается
Оказывается, мультипликативные линейные функционалы от C*(грамм)после подходящей идентификации - это именно символы грамм, и преобразование Гельфанда, когда оно ограничено плотным подмножеством L1(грамм) - преобразование Фурье – Понтрягина.
Компактные неабелевы группы
Преобразование Фурье также может быть определено для функций на неабелевой группе при условии, что группа компактный. Устранение предположения, что основная группа является абелевой, неприводимые унитарные представления не всегда должны быть одномерными. Это означает, что преобразование Фурье на неабелевой группе принимает значения как операторы гильбертова пространства.[43] Преобразование Фурье на компактных группах является основным инструментом в теория представлений[44] и некоммутативный гармонический анализ.
Позволять грамм быть компактным Хаусдорф топологическая группа. Позволять Σ обозначают совокупность всех классов изоморфизма конечномерных неприводимых унитарные представления, наряду с определенным выбором представительства U(σ) на Гильбертово пространство ЧАСσ конечной размерности dσ для каждого σ ∈ Σ. Если μ конечный Мера Бореля на грамм, то преобразование Фурье – Стилтьеса μ оператор на ЧАСσ определяется
куда U(σ) комплексно-сопряженное представление U(σ) действующий на ЧАСσ. Если μ является абсолютно непрерывный с уважением к левоинвариантная вероятностная мера λ на грамм, представлен в качестве
для некоторых ж ∈ L1(λ), идентифицируется преобразование Фурье ж с преобразованием Фурье – Стилтьеса μ.
Отображение
определяет изоморфизм между Банахово пространство M(грамм) конечных борелевских мер (см. RCA Space) и замкнутое подпространство банахова пространства C∞(Σ) состоящий из всех последовательностей E = (Eσ) проиндексировано Σ (ограниченных) линейных операторов Eσ : ЧАСσ → ЧАСσ для которого норма
конечно. "теорема свертки"утверждает, что, кроме того, этот изоморфизм банаховых пространств на самом деле является изометрическим изоморфизмом C * алгебры в подпространство C∞(Σ). Умножение на M(грамм) дан кем-то свертка мер и инволюции *, определяемой
и C∞(Σ) имеет естественный C*-алгебра как операторы гильбертова пространства.
В Теорема Питера – Вейля выполняется, и вариант формулы обращения Фурье (Теорема Планшереля) следует: если ж ∈ L2(грамм), тогда
где суммирование понимается как сходящееся в L2 смысл.
Обобщение преобразования Фурье на некоммутативную ситуацию также частично способствовало развитию некоммутативная геометрия.[нужна цитата] В этом контексте категорическое обобщение преобразования Фурье на некоммутативные группы имеет вид Двойственность Таннаки – Крейна, который заменяет группу символов категорией представлений. Однако это теряет связь с гармоническими функциями.
Альтернативы
В обработка сигналов термины, функция (времени) - это представление сигнала с идеальным разрешение по времени, но нет частотной информации, в то время как преобразование Фурье имеет идеальную разрешение по частоте, но нет информации о времени: величина преобразования Фурье в точке - это то, сколько частотного содержимого есть, но местоположение задается только фазой (аргумент преобразования Фурье в точке), и стоячие волны не локализованы во времени - синусоида продолжается до бесконечности, не затухая. Это ограничивает полезность преобразования Фурье для анализа сигналов, локализованных во времени, в частности переходные процессы, или любой сигнал конечной степени.
В качестве альтернативы преобразованию Фурье в частотно-временной анализ, используются частотно-временные преобразования или частотно-временные распределения для представления сигналов в форме, содержащей некоторую информацию о времени и некоторую частотную информацию - по принципу неопределенности между ними существует компромисс. Это могут быть обобщения преобразования Фурье, такие как кратковременное преобразование Фурье или же дробное преобразование Фурье, или другие функции для представления сигналов, как в вейвлет-преобразования и чирплет преобразовывает, с вейвлет-аналогом (непрерывного) преобразования Фурье, являющегося непрерывное вейвлет-преобразование.[19]
Приложения
Анализ дифференциальных уравнений
Возможно, наиболее важным применением преобразования Фурье является решение уравнения в частных производныхТаким образом можно трактовать многие уравнения математической физики XIX века. Фурье изучил уравнение теплопроводности, которое в одномерном и безразмерных единицах имеет вид
Пример, который мы приведем, немного более сложный, - это волновое уравнение в одном измерении,
Как обычно, проблема не в том, чтобы найти решение: их бесконечно много. Проблема заключается в так называемой «краевой задаче»: найти решение, удовлетворяющее «граничным условиям»
Здесь, ж и грамм даны функции. Для уравнения теплопроводности может потребоваться только одно граничное условие (обычно первое). Но для волнового уравнения еще существует бесконечно много решений у удовлетворяющие первому граничному условию. Но когда накладываются оба условия, есть только одно возможное решение.
Проще найти преобразование Фурье ŷ решения, чем искать решение напрямую. Это связано с тем, что преобразование Фурье переводит дифференцирование в умножение на двойственную по Фурье переменную, и поэтому уравнение в частных производных, применяемое к исходной функции, преобразуется в умножение на полиномиальные функции двойственных переменных, применяемых к преобразованной функции. После ŷ определяется, мы можем применить обратное преобразование Фурье, чтобы найти у.
Метод Фурье заключается в следующем. Во-первых, обратите внимание, что любая функция форм
удовлетворяет волновому уравнению. Это называется элементарными решениями.
Во-вторых, заметим, что поэтому любой интеграл
(для произвольных а+, а−, б+, б−) удовлетворяет волновому уравнению. (Этот интеграл представляет собой разновидность непрерывной линейной комбинации, а уравнение является линейным.)
Теперь это напоминает формулу синтеза Фурье функции. Фактически, это реальное обратное преобразование Фурье а± и б± в переменной Икс.
Третий шаг - изучить, как найти конкретные неизвестные функции коэффициентов. а± и б± это приведет к у удовлетворяющие граничным условиям. Нас интересуют значения этих решений при т = 0. Итак, мы установим т = 0. Предполагая, что условия, необходимые для обращения Фурье, выполнены, мы можем затем найти преобразования синуса и косинуса Фурье (в переменной Икс) обеих сторон и получаем
и
Аналогично, взяв производную от у относительно т а затем применение преобразований синуса Фурье и косинуса дает
и
Это четыре линейных уравнения для четырех неизвестных а± и б±, в терминах синусоидальных и косинусных преобразований Фурье граничных условий, которые легко решаются элементарной алгеброй при условии, что эти преобразования могут быть найдены.
Таким образом, мы выбрали набор элементарных решений, параметризованных ξ, общим решением которой была бы (непрерывная) линейная комбинация в виде интеграла по параметру ξ. Но этот интеграл был в виде интеграла Фурье. Следующим шагом было выразить граничные условия через эти интегралы и установить их равными заданным функциям ж и грамм. Но эти выражения также приняли форму интеграла Фурье из-за свойств преобразования Фурье производной. Последним шагом было использование обращения Фурье путем применения преобразования Фурье к обеим сторонам, что позволило получить выражения для коэффициентов функции а± и б± в рамках заданных граничных условий ж и грамм.
С более высокой точки зрения процедуру Фурье можно переформулировать более концептуально. Поскольку есть две переменные, мы будем использовать преобразование Фурье в обеих Икс и т вместо того, чтобы действовать, как Фурье, который преобразовывал только пространственные переменные. Обратите внимание, что ŷ следует рассматривать в смысле распределения, поскольку у(Икс, т) не будет L1: как волна, он будет сохраняться во времени и, следовательно, не является временным явлением. Но оно будет ограниченным, и поэтому его преобразование Фурье можно определить как распределение. Операционные свойства преобразования Фурье, относящиеся к этому уравнению, заключаются в том, что оно требует дифференцирования по Икс к умножению на 2πiξ и дифференцирование по т к умножению на 2πесли куда ж это частота. Тогда волновое уравнение превращается в алгебраическое уравнение в ŷ:
Это эквивалентно требованию ŷ(ξ, ж ) = 0 пока не ξ = ±ж. Это сразу же объясняет, почему сделанный нами ранее выбор элементарных решений сработал так хорошо: очевидно, f̂ = δ(ξ ± ж ) будут решения. Применяя обращение Фурье к этим дельта-функциям, мы получаем выбранные ранее элементарные решения. Но с более высокой точки зрения, мы не выбираем элементарные решения, а скорее рассматриваем пространство всех распределений, которые поддерживаются на (вырожденной) конике. ξ2 − ж2 = 0.
Мы также можем рассматривать распределения, поддерживаемые на конике, которые задаются распределениями одной переменной на прямой ξ = ж плюс раздачи на линии ξ = −ж следующим образом: если ϕ это любая тестовая функция,
куда s+, и s−, являются распределениями одной переменной.
Тогда обращение Фурье дает для граничных условий нечто очень похожее на то, что мы имели более конкретно выше (положим ϕ(ξ, ж ) = е2πя(xξ+tf ), который явно имеет полиномиальный рост):
и
Теперь, как и раньше, применяя преобразование Фурье с одной переменной по переменной Икс этим функциям Икс дает два уравнения в двух неизвестных распределениях s± (которые можно принять за обычные функции, если граничные условия L1 или же L2).
С вычислительной точки зрения недостатком, конечно же, является то, что нужно сначала вычислить преобразования Фурье граничных условий, затем собрать из них решение, а затем вычислить обратное преобразование Фурье. Формулы с замкнутыми формулами встречаются редко, за исключением случаев, когда можно использовать некоторую геометрическую симметрию, а численные расчеты затруднены из-за колебательного характера интегралов, что делает сходимость медленной и затрудняет оценку. Для практических расчетов часто используются другие методы.
В двадцатом веке эти методы были распространены на все линейные дифференциальные уравнения в частных производных с полиномиальными коэффициентами, а также за счет расширения понятия преобразования Фурье, включая интегральные операторы Фурье, а также некоторые нелинейные уравнения.
Спектроскопия с преобразованием Фурье
Преобразование Фурье также используется в ядерный магнитный резонанс (ЯМР) и в других видах спектроскопия, например инфракрасный (FTIR). В ЯМР сигнал экспоненциальной формы затухания свободной индукции (FID) регистрируется во временной области и преобразуется Фурье в форму линии Лоренца в частотной области. Преобразование Фурье также используется в магнитно-резонансная томография (МРТ) и масс-спектрометрии.
Квантовая механика
Преобразование Фурье полезно в квантовая механика двумя разными способами. Начнем с того, что основная концептуальная структура квантовой механики постулирует существование пар дополнительные переменные, связанных Принцип неопределенности Гейзенберга. Например, в одном измерении пространственная переменная q , скажем, частицы, можно измерить только квантово-механическим методом "оператор позиции"ценой потери информации об импульсе п частицы. Следовательно, физическое состояние частицы можно описать либо функцией, называемой «волновой функцией», q или функцией п но не функцией обеих переменных. Переменная п называется сопряженной переменной к q. В классической механике физическое состояние частицы (существующее в одном измерении для простоты изложения) могло бы быть задано путем присвоения определенных значений обоим п и q одновременно. Таким образом, набор всех возможных физических состояний представляет собой двумерное вещественное векторное пространство с п-ось и qось называется фазовое пространство.
Напротив, квантовая механика выбирает поляризацию этого пространства в том смысле, что она выбирает подпространство половинной размерности, например, q-ось одна, но вместо того, чтобы рассматривать только точки, берет набор всех комплексных "волновых функций" на этой оси. Тем не менее, выбирая п-ось - это одинаково допустимая поляризация, дающая другое представление набора возможных физических состояний частицы, которое связано с первым представлением преобразованием Фурье
Физически реализуемые состояния: L2, а значит, по теореме Планшереля их преобразования Фурье также L2. (Обратите внимание, что поскольку q в единицах расстояния и п выражается в единицах количества движения, наличие постоянной Планка в показателе экспоненты делает показатель безразмерный, так, как это должно быть.)
Следовательно, преобразование Фурье может использоваться для перехода от одного способа представления состояния частицы с помощью волновой функции положения к другому способу представления состояния частицы: с помощью волновой функции количества движения. Возможно бесконечно много различных поляризаций, и все они одинаково действительны. Иногда бывает удобно преобразовывать состояния из одного представления в другое.
Другое использование преобразования Фурье как в квантовой механике, так и в квантовая теория поля заключается в решении применимого волнового уравнения. В нерелятивистской квантовой механике Уравнение Шредингера для изменяющейся во времени волновой функции в одномерном пространстве, не подверженной внешним силам, равно
Это то же самое, что и уравнение теплопроводности, за исключением наличия мнимой единицы я. Для решения этого уравнения можно использовать методы Фурье.
При наличии потенциала, задаваемого функцией потенциальной энергии V(Икс), уравнение принимает вид
«Элементарные решения», как мы называли их выше, являются так называемыми «стационарными состояниями» частицы, и алгоритм Фурье, как описано выше, все еще можно использовать для решения краевой задачи будущей эволюции ψ учитывая его значения для т = 0. Ни один из этих подходов не имеет большого практического применения в квантовой механике. Краевые задачи и временная эволюция волновой функции не представляют большого практического интереса: наиболее важны стационарные состояния.
В релятивистской квантовой механике уравнение Шредингера становится волновым уравнением, как это было обычно в классической физике, за исключением того, что рассматриваются комплексные волны. Простым примером, при отсутствии взаимодействий с другими частицами или полями, является бесплатное одномерное уравнение Клейна – Гордона – Шредингера – Фока, на этот раз в безразмерных единицах:
Это, с математической точки зрения, то же самое, что и волновое уравнение классической физики, решенное выше (но с комплексной волной, которая не имеет значения в методах). Это очень полезно в квантовой теории поля: каждую отдельную составляющую Фурье волны можно рассматривать как отдельный гармонический осциллятор, а затем квантовать, процедура, известная как «второе квантование». Методы Фурье были адаптированы для работы с нетривиальными взаимодействиями.
Обработка сигналов
Преобразование Фурье используется для спектрального анализа временных рядов. Однако в рамках статистической обработки сигналов преобразование Фурье обычно не применяется к самому сигналу. Даже если реальный сигнал действительно является переходным, на практике было обнаружено, что рекомендуется моделировать сигнал с помощью функции (или, альтернативно, случайного процесса), которая является стационарной в том смысле, что ее характерные свойства постоянны во все времена. Преобразования Фурье такой функции не существует в обычном смысле, и было обнаружено, что для анализа сигналов более полезным вместо этого использовать преобразование Фурье ее автокорреляционной функции.
Автокорреляционная функция р функции ж определяется
Эта функция является функцией запаздывания τ проходит между значениями ж быть коррелированным.
Для большинства функций ж что происходит на практике, р является ограниченной четной функцией запаздывания τ а для типичных зашумленных сигналов он оказывается равномерно непрерывным с максимумом при τ = 0.
Функция автокорреляции, более корректно называемая функцией автоковариации, если она не нормализована каким-либо подходящим способом, измеряет силу корреляции между значениями ж разделены временной задержкой. Это способ поиска корреляции ж со своим прошлым. Это полезно даже для других статистических задач, помимо анализа сигналов. Например, если ж (т) представляет температуру во время т, ожидается сильная корреляция с температурой с интервалом в 24 часа.
Он обладает преобразованием Фурье,
Это преобразование Фурье называется функцией спектральной плотности мощности ж. (Если сначала все периодические компоненты не отфильтрованы из ж, этот интеграл будет расходиться, но такие периодичности легко отфильтровать.)
Спектр мощности, на что указывает эта функция плотности п, измеряет величину дисперсии данных по частоте ξ. В электрических сигналах дисперсия пропорциональна средней мощности (энергии в единицу времени), поэтому спектр мощности описывает, насколько разные частоты влияют на среднюю мощность сигнала. Этот процесс называется спектральным анализом временных рядов и аналогичен обычному анализу дисперсии данных, которые не являются временными рядами (ANOVA).
Знание того, какие частоты являются «важными» в этом смысле, имеет решающее значение для правильной конструкции фильтров и для правильной оценки измерительных приборов. Это также может быть полезно для научного анализа явлений, ответственных за получение данных.
Спектр мощности сигнала также может быть приблизительно измерен непосредственно путем измерения средней мощности, которая остается в сигнале после того, как все частоты за пределами узкой полосы были отфильтрованы.
Спектральный анализ проводится и для визуальных сигналов. Спектр мощности игнорирует все фазовые соотношения, что достаточно для многих целей, но для видеосигналов также должны использоваться другие типы спектрального анализа, по-прежнему с использованием преобразования Фурье в качестве инструмента.
Другие обозначения
Другие общие обозначения для f̂ (ξ) включают:
Обозначая преобразование Фурье заглавной буквой, соответствующей букве преобразуемой функции (например, ж (Икс) и F(ξ)) особенно распространено в науке и технике. В электронике омега (ω) часто используется вместо ξ из-за его интерпретации как угловая частота, иногда его записывают как F( jω), куда j это мнимая единица, чтобы указать его связь с Преобразование Лапласа, а иногда неофициально записывается как F(2πж ) чтобы использовать обычную частоту. В некоторых контекстах, например в физике элементарных частиц, тот же символ может использоваться как для функции, так и для преобразования Фурье, причем эти два аргумент: будет относиться к преобразованию Фурье из-за аргумента импульса, в то время как будет ссылаться на исходную функцию из-за позиционного аргумента. Хотя тильды могут использоваться как в для обозначения преобразований Фурье тильды могут также использоваться для обозначения модификации величины с более Инвариант Лоренца форма, например , поэтому необходимо соблюдать осторожность.
Интерпретация сложной функции f̂ (ξ) может помочь выразить это в полярная координата форма
в терминах двух реальных функций А(ξ) и φ(ξ) куда:
это амплитуда и
это фаза (видеть функция arg).
Тогда обратное преобразование можно записать:
что представляет собой рекомбинацию всех частотных составляющих ж (Икс). Каждый компонент представляет собой комплекс синусоида формы е2πixξ чья амплитуда А(ξ) и чьи начальные угол фазы (в Икс = 0) является φ(ξ).
Преобразование Фурье можно рассматривать как отображение на функциональных пространствах. Это отображение здесь обозначено F и F( ж ) используется для обозначения преобразования Фурье функции ж. Это отображение линейно, что означает, что F также можно рассматривать как линейное преобразование в функциональном пространстве и означает, что стандартные обозначения в линейной алгебре применения линейного преобразования к вектору (здесь функция ж ) можно использовать для записи F ж вместо F( ж ). Поскольку результатом применения преобразования Фурье снова является функция, нас может интересовать значение этой функции, вычисленное при значении ξ для его переменной, и это обозначается либо как F ж (ξ) или как ( F ж )(ξ). Обратите внимание, что в первом случае подразумевается, что F применяется сначала к ж а затем результирующая функция оценивается на ξ, А не наоборот.
В математике и различных прикладных науках часто бывает необходимо различать функцию ж и ценность ж когда его переменная равна Икс, обозначенный ж (Икс). Это означает, что такие обозначения, как F( ж (Икс)) формально можно интерпретировать как преобразование Фурье значений ж в Икс. Несмотря на этот недостаток, предыдущие обозначения появляются часто, часто, когда конкретная функция или функция определенной переменной должна быть преобразована. Например,
иногда используется, чтобы выразить, что преобразование Фурье прямоугольная функция это функция sinc, или же
используется для выражения свойства сдвига преобразования Фурье.
Обратите внимание, что последний пример верен только в предположении, что преобразованная функция является функцией Иксне из Икс0.
Прочие соглашения
Преобразование Фурье также можно записать в терминах угловая частота:
чьи подразделения радианы в секунду.
Замена ξ = ω/2π в приведенные выше формулы дает следующее соглашение:
Согласно этому соглашению, обратное преобразование становится:
В отличие от соглашения, принятого в этой статье, когда преобразование Фурье определяется таким образом, оно больше не является унитарное преобразование на L2(ℝп). Также меньше симметрии между формулами преобразования Фурье и его обратного.
Другое соглашение - разделить фактор (2π)п равномерно между преобразованием Фурье и обратным ему, что приводит к определениям:
Согласно этому соглашению преобразование Фурье снова является унитарным преобразованием на L2(ℝп). Он также восстанавливает симметрию между преобразованием Фурье и обратным ему.
Варианты всех трех соглашений могут быть созданы путем сопряжения комплексно-экспоненциального ядро как прямого, так и обратного преобразования. Знаки должны быть противоположными. В остальном выбор (опять же) является делом условностей.
| обычная частота ξ (Гц) | унитарный | |
|---|---|---|
| угловая частота ω (рад / с) | унитарный | |
| неунитарный |
| обычная частота ξ (Гц) | унитарный | |
|---|---|---|
| угловая частота ω (рад / с) | унитарный | |
| неунитарный |
Как обсуждалось выше, характеристическая функция случайной величины совпадает с Преобразование Фурье – Стилтьеса меры распределения, но в этом контексте типично использовать другое соглашение для констант. Обычно характеристическая функция определяется
Как и в случае с условием "неунитарная угловая частота" выше, коэффициент 2π не входит ни в нормирующую константу, ни в экспоненту. В отличие от любого из приведенных выше соглашений, это соглашение принимает противоположный знак в экспоненте.
Методы расчета
Подходящий метод вычисления во многом зависит от того, как представлена исходная математическая функция и от желаемой формы выходной функции.
Поскольку основное определение преобразования Фурье - это интеграл, функции, которые могут быть выражены как выражения в закрытой форме обычно вычисляются путем аналитической обработки интеграла, чтобы получить в результате выражение в замкнутой форме в сопряженной переменной преобразования Фурье. Это метод, используемый для создания таблиц преобразований Фурье,[45] включая те, что указаны в таблице ниже (Преобразование Фурье # Таблицы важных преобразований Фурье).
Многие системы компьютерной алгебры, такие как Matlab и Mathematica которые способны символическая интеграция способны аналитически вычислять преобразования Фурье. Например, чтобы вычислить преобразование Фурье ж (т) = cos (6πт) е−πт2 можно ввести команду интегрировать cos (6 * pi * t) exp (−pi * t ^ 2) exp (-i * 2 * pi * f * t) от -inf до inf в вольфрам Альфа.
Численное интегрирование замкнутых функций
Если входная функция находится в замкнутой форме, а желаемая выходная функция представляет собой серию упорядоченных пар (например, таблица значений, из которой может быть сгенерирован график) в указанной области, то преобразование Фурье может быть сгенерировано с помощью численное интегрирование at each value of the Fourier conjugate variable (frequency, for example) for which a value of the output variable is desired.[46] Note that this method requires computing a separate numerical integration for each value of frequency for which a value of the Fourier transform is desired.[47][48] The numerical integration approach works on a much broader class of functions than the analytic approach, because it yields results for functions that do not have closed form Fourier transform integrals.
Численное интегрирование серии упорядоченных пар
If the input function is a series of ordered pairs (for example, a time series from measuring an output variable repeatedly over a time interval) then the output function must also be a series of ordered pairs (for example, a complex number vs. frequency over a specified domain of frequencies), unless certain assumptions and approximations are made allowing the output function to be approximated by a closed-form expression. In the general case where the available input series of ordered pairs are assumed be samples representing a continuous function over an interval (amplitude vs. time, for example), the series of ordered pairs representing the desired output function can be obtained by numerical integration of the input data over the available interval at each value of the Fourier conjugate variable (frequency, for example) for which the value of the Fourier transform is desired.[49]
Explicit numerical integration over the ordered pairs can yield the Fourier transform output value for any desired value of the conjugate Fourier transform variable (frequency, for example), so that a spectrum can be produced at any desired step size and over any desired variable range for accurate determination of amplitudes, frequencies, and phases corresponding to isolated peaks. Unlike limitations in DFT and FFT methods, explicit numerical integration can have any desired step size and compute the Fourier transform over any desired range of the conjugate Fourier transform variable (for example, frequency).
Дискретные преобразования Фурье и быстрые преобразования Фурье
If the ordered pairs representing the original input function are equally spaced in their input variable (for example, equal time steps), then the Fourier transform is known as a дискретное преобразование Фурье (DFT), which can be computed either by explicit numerical integration, by explicit evaluation of the DFT definition, or by быстрое преобразование Фурье (FFT) methods. In contrast to explicit integration of input data, use of the DFT and FFT methods produces Fourier transforms described by ordered pairs of step size equal to the reciprocal of the original sampling interval. For example, if the input data is sampled every 10 seconds, the output of DFT and FFT methods will have a 0.1 Hz frequency spacing.
Таблицы важных преобразований Фурье
The following tables record some closed-form Fourier transforms. Для функций ж (Икс), грамм(Икс) и час(Икс) denote their Fourier transforms by f̂, грамм, и час соответственно. Only the three most common conventions are included. It may be useful to notice that entry 105 gives a relationship between the Fourier transform of a function and the original function, which can be seen as relating the Fourier transform and its inverse.
Функциональные отношения, одномерные
The Fourier transforms in this table may be found in Erdélyi (1954) или же Kammler (2000, appendix).
| Функция | преобразование Фурье unitary, ordinary frequency | преобразование Фурье unitary, angular frequency | преобразование Фурье non-unitary, angular frequency | Замечания | |
|---|---|---|---|---|---|
| Определение | |||||
| 101 | Линейность | ||||
| 102 | Shift in time domain | ||||
| 103 | Shift in frequency domain, dual of 102 | ||||
| 104 | Scaling in the time domain. Если |а| is large, then ж (топор) is concentrated around 0 and spreads out and flattens. | ||||
| 105 | Двойственность. Здесь f̂ needs to be calculated using the same method as Fourier transform column. Results from swapping "dummy" variables of Икс и ξ или же ω или же ν. | ||||
| 106 | |||||
| 107 | This is the dual of 106 | ||||
| 108 | Обозначение ж ∗ грамм обозначает свертка из ж и грамм — this rule is the теорема свертки | ||||
| 109 | This is the dual of 108 | ||||
| 110 | За ж (Икс) purely real | Hermitian symmetry. z указывает на комплексно сопряженный. | |||
| 111 | За ж (Икс) purely real and четное | f̂ (ξ), f̂ (ω) и f̂ (ν) are purely real even functions. | |||
| 112 | За ж (Икс) purely real and странный | f̂ (ξ), f̂ (ω) и f̂ (ν) are purely воображаемый odd functions. | |||
| 113 | За ж (Икс) чисто воображаемый | z указывает на комплексно сопряженный. | |||
| 114 | Комплексное сопряжение, generalization of 110 and 113 | ||||
| 115 | This follows from rules 101 and 103 using Формула Эйлера: | ||||
| 116 | This follows from 101 and 103 using Формула Эйлера: | ||||
Функции, интегрируемые с квадратом, одномерные
The Fourier transforms in this table may be found in Campbell & Foster (1948), Erdélyi (1954), или же Kammler (2000, appendix).
| Функция | преобразование Фурье unitary, ordinary frequency | преобразование Фурье unitary, angular frequency | преобразование Фурье non-unitary, angular frequency | Замечания | |
|---|---|---|---|---|---|
| 201 | В rectangular pulse и нормализованный функция sinc, here defined as sinc(Икс) = sin(πИкс)/πИкс | ||||
| 202 | Dual of rule 201. The прямоугольная функция is an ideal low-pass filter, а функция sinc это non-causal impulse response of such a filter. В функция sinc is defined here as sinc(Икс) = sin(πИкс)/πИкс | ||||
| 203 | Функция tri(Икс) это triangular function | ||||
| 204 | Dual of rule 203. | ||||
| 205 | Функция ты(Икс) это Heaviside unit step function и а > 0. | ||||
| 206 | This shows that, for the unitary Fourier transforms, the Функция Гаусса е−αx2 is its own Fourier transform for some choice of α. For this to be integrable we must have Re (α) > 0. | ||||
| 207 | This is known as the complex quadratic-phase sinusoid, or the "chirp" function.[50] | ||||
| 208 | За Re (а) > 0. That is, the Fourier transform of a two-sided decaying exponential function это Lorentzian function. | ||||
| 209 | Гиперболический секанс is its own Fourier transform | ||||
| 210 | ЧАСп это пth-order Многочлен Эрмита. Если а = 1 then the Gauss–Hermite functions are собственные функции of the Fourier transform operator. For a derivation, see Многочлен Эрмита. The formula reduces to 206 for п = 0. |
Распределения, одномерные
The Fourier transforms in this table may be found in Erdélyi (1954) или же Kammler (2000, appendix).
| Функция | преобразование Фурье unitary, ordinary frequency | преобразование Фурье unitary, angular frequency | преобразование Фурье non-unitary, angular frequency | Замечания | |
|---|---|---|---|---|---|
| 301 | Распространение δ(ξ) обозначает Дельта-функция Дирака. | ||||
| 302 | Двойное правило 301. | ||||
| 303 | Это следует из 103 и 301. | ||||
| 304 | Это следует из правил 101 и 303 с использованием Формула Эйлера: | ||||
| 305 | Это следует из 101 и 303, используя | ||||
| 306 | Это следует из 101 и 207 с использованием | ||||
| 307 | Это следует из 101 и 207 с использованием | ||||
| 308 | Здесь, п это натуральное число и δ(п)(ξ) это п-я производная распределения дельта-функции Дирака. Это правило следует из правил 107 и 301. Комбинируя это правило с правилом 101, мы можем преобразовать все многочлены. | ||||
| Двойник правила 308. δ(п)(ξ) это п-я производная распределения дельта-функции Дирака. Это правило следует из 106 и 302. | |||||
| 309 | Здесь sgn (ξ) это функция знака. Обратите внимание, что 1/Икс это не раздача. Необходимо использовать Главное значение Коши при тестировании против Функции Шварца. Это правило полезно при изучении Преобразование Гильберта. | ||||
| 310 | 1/Иксп это однородное распределение определяется распределительной производной | ||||
| 311 | Эта формула верна для 0 > α > −1. За α > 0 в начале координат возникают некоторые сингулярные члены, которые можно найти, дифференцируя 318. Если Re α > −1, тогда |Икс|α является локально интегрируемой функцией и, следовательно, умеренным распределением. Функция α ↦ |Икс|α - голоморфная функция из правой полуплоскости в пространство умеренных распределений. Он допускает уникальное мероморфное расширение до умеренного распределения, также обозначаемого |Икс|α за α ≠ −2, −4,... (Видеть однородное распределение.) | ||||
| Частный случай 311. | |||||
| 312 | Двойственное правило 309. На этот раз преобразования Фурье нужно рассматривать как Главное значение Коши. | ||||
| 313 | Функция ты(Икс) это Хевисайд функция шага единицы; это следует из правил 101, 301 и 312. | ||||
| 314 | Эта функция известна как Гребень Дирака функция. Этот результат может быть получен из 302 и 102 вместе с тем фактом, что как раздачи. | ||||
| 315 | Функция J0(Икс) это нулевой порядок Функция Бесселя первого рода. | ||||
| 316 | Это обобщение 315. Функция Jп(Икс) это пй заказ Функция Бесселя первого рода. Функция Тп(Икс) это Многочлен Чебышева первого рода. | ||||
| 317 | γ это Константа Эйлера – Маскерони. | ||||
| 318 | Эта формула верна для 1 > α > 0. Используйте дифференцирование, чтобы получить формулу для более высоких показателей. ты - функция Хевисайда. |
Двумерные функции
| Функция | преобразование Фурье унитарная, обычная частота | преобразование Фурье унитарная, угловая частота | преобразование Фурье неунитарная, угловая частота | Замечания | |
|---|---|---|---|---|---|
| 400 | Переменные ξИкс, ξу, ωИкс, ωу, νИкс, νу настоящие числа. Интегралы берутся по всей плоскости. | ||||
| 401 | Обе функции являются гауссианами, которые могут не иметь единичного объема. | ||||
| 402 | Функция определяется круг (р) = 1 за 0 ≤ р ≤ 1, и 0 в противном случае. В результате получается амплитудное распределение Диск Эйри, и выражается через J1 (заказ-1 Функция Бесселя первого рода).[51] | ||||
| 403 | Это Преобразование Ганкеля из р−1, двумерное "самопреобразование" Фурье.[50] | ||||
| 404 |
Формулы для общих п-мерные функции
| Функция | преобразование Фурье унитарная, обычная частота | преобразование Фурье унитарная, угловая частота | преобразование Фурье неунитарная, угловая частота | Замечания | |
|---|---|---|---|---|---|
| 500 | |||||
| 501 | Функция χ[0, 1] это индикаторная функция интервала [0, 1]. Функция Γ (Икс) это гамма-функция. Функция Jп/2 + δ - функция Бесселя первого рода с порядком п/2 + δ. Принимая п = 2 и δ = 0 производит 402.[52] | ||||
| 502 | Видеть Потенциал Рисса где постоянная определяется выражением Формула также верна для всех α ≠ −п, −п − 1, ... путем аналитического продолжения, но тогда функцию и ее преобразования Фурье следует понимать как подходящие регуляризованные умеренные распределения. Видеть однородное распределение.[примечание 6] | ||||
| 503 | Это формула для многомерное нормальное распределение нормализовано к 1 со средним значением 0. Переменные, выделенные жирным шрифтом, - это векторы или матрицы. Следуя обозначениям вышеупомянутой страницы, Σ = σ σТ и Σ−1 = σ−T σ−1 | ||||
| 504 | Здесь[53] Re (α) > 0 |
Смотрите также
- Обработка аналогового сигнала
- Полоса Биверса – Липсона
- Дискретное преобразование Фурье
- Быстрое преобразование Фурье
- Интегральный оператор Фурье
- Теорема обращения Фурье
- Множитель Фурье
- Ряд Фурье
- Преобразование синуса Фурье
- Преобразование Фурье – Делиня
- Преобразование Фурье – Мукаи
- Дробное преобразование Фурье
- Косвенное преобразование Фурье
- Интегральное преобразование
- Преобразование Лапласа
- Линейное каноническое преобразование
- Преобразование Меллина
- Многомерное преобразование
- NGC 4622, особенно изображение NGC 4622 преобразование Фурье м = 2.
- Нелокальный оператор
- Квантовое преобразование Фурье
- Кратковременное преобразование Фурье
- Спектральная плотность
- Символическая интеграция
- Дисперсионное преобразование Фурье во времени
- Преобразование (математика)
Замечания
- ^ С точностью до мнимого постоянного множителя, величина которого зависит от используемого соглашения о преобразовании Фурье.
- ^ В зависимости от приложения Интеграл Лебега, распределительный, или другой подход может быть наиболее подходящим.
- ^ Вретблад (2000) обеспечивает твердое обоснование этих формальных процедур, не вдаваясь слишком глубоко в функциональный анализ или теория распределений.
- ^ В релятивистская квантовая механика встречаются векторные преобразования Фурье многокомпонентных волновых функций. В квантовая теория поля, часто используются операторнозначные преобразования Фурье операторнозначных функций пространства-времени, см., например, Грейнер и Райнхардт (1996).
- ^ Функция также сигнал с частотой , но интеграл, очевидно, дает одинаковые отклики на обоих и , что также согласуется с Формула Эйлера:
- ^ В Гельфанд и Шилов 1964, п. 363, с неунитарными соглашениями этой таблицы, преобразование дано быть
откуда это следует, с .
Примечания
- ^ Кайзер 1994, п. 29.
- ^ Рахман 2011, п. 11.
- ^ «Условные обозначения в электромагнитных (ЭМ) волнах» (PDF).
- ^ Фурье 1822 г., п. 525.
- ^ Фурье 1878 г., п. 408.
- ^ (Иордания 1883) доказывает на стр. 216–226 Интегральная теорема Фурье до изучения рядов Фурье.
- ^ Титчмарш 1986, п. 1.
- ^ Рахман 2011, п. 10.
- ^ Фолланд 1989.
- ^ Фурье 1822 г..
- ^ Танежа 2008, п. 192.
- ^ а б Штейн и Шакарчи 2003.
- ^ а б c d е Пинский 2002.
- ^ а б c d е Кацнельсон 1976.
- ^ а б c d е ж Штайн и Вайс, 1971 г..
- ^ Рудин 1987, п. 187.
- ^ Рудин 1987, п. 186.
- ^ а б Duoandikoetxea 2001.
- ^ а б Боашаш 2003.
- ^ Кондон 1937.
- ^ Хау 1980.
- ^ Пэйли и Винер 1934.
- ^ Гельфанд и Виленкин 1964.
- ^ Кириллов и Гвишиани 1982.
- ^ Clozel & Delorme 1985С. 331–333.
- ^ де Гроот и Мазур 1984, п. 146.
- ^ Чампени 1987, п. 80.
- ^ а б c Колмогоров и Фомин 1999.
- ^ Винер 1949.
- ^ Чампени 1987, п. 63.
- ^ Виддер и Винер 1938, п. 537.
- ^ Пинский 2002, п. 131.
- ^ Штейн и Шакарчи 2003, п. 158.
- ^ Чатфилд 2004, п. 113.
- ^ Фурье 1822 г., п. 441.
- ^ Пуанкаре 1895, п. 102.
- ^ Уиттакер и Ватсон, 1927 г., п. 188.
- ^ Графакос 2004.
- ^ Grafakos & Teschl 2013.
- ^ «Прикладной анализ Фурье и элементы современной обработки сигналов, лекция 3» (PDF). 12 января 2016 г.. Получено 2019-10-11.
- ^ Штайн и Вайс, 1971 г., Thm. 2.3.
- ^ Пинский 2002, п. 256.
- ^ Хьюитт и Росс 1970, Глава 8.
- ^ Кнапп 2001.
- ^ Градштейн и др. 2015 г..
- ^ Press et al. 1992 г..
- ^ Бейли и Сварцтраубер 1994.
- ^ Ладо 1971.
- ^ Симонен и Олкконен 1985.
- ^ а б Младший, Роджер Л. Истон (2010). Методы Фурье в визуализации. Джон Вили и сыновья. ISBN 978-0-470-68983-7. Получено 26 мая 2020.
- ^ Штайн и Вайс, 1971 г., Thm. IV.3.3.
- ^ Штайн и Вайс, 1971 г., Thm. 4.15.
- ^ Штайн и Вайс, 1971 г., п. 6.
Рекомендации
- Бейли, Дэвид Х .; Swarztrauber, Пол Н. (1994), «Быстрый метод численной оценки непрерывных преобразований Фурье и Лапласа» (PDF), Журнал SIAM по научным вычислениям, 15 (5): 1105–1110, CiteSeerX 10.1.1.127.1534, Дои:10.1137/0915067.
- Боашаш, Б., изд. (2003), Частотно-временной анализ и обработка сигналов: полный справочник, Oxford: Elsevier Science, ISBN 978-0-08-044335-5.
- Бохнер, С.; Чандрасекхаран, К. (1949), Преобразования Фурье, Princeton University Press.
- Брейсуэлл, Р. Н. (2000), Преобразование Фурье и его приложения (3-е изд.), Бостон: McGraw-Hill, ISBN 978-0-07-116043-8.
- Кэмпбелл, Джордж; Фостер, Рональд (1948), Интегралы Фурье для практических приложений, Нью-Йорк: D. Van Nostrand Company, Inc..
- Чампени, округ Колумбия (1987), Справочник теорем Фурье, Издательство Кембриджского университета.
- Чатфилд, Крис (2004), Анализ временных рядов: введение, Тексты по статистике (6-е изд.), Лондон: Chapman & Hall / CRC, ISBN 9780203491683.
- Клозель, Лоран; Делорм, Патрис (1985), "Sur le théorème de Paley-Wiener invariant pour les groupes de Lie réductifs réels", Comptes Rendus de l'Académie des Sciences, Série I, 300: 331–333.
- Кондон, Э. У. (1937), «Погружение преобразования Фурье в непрерывную группу функциональных преобразований», Proc. Natl. Акад. Sci., 23 (3): 158–164, Bibcode:1937ПНАС ... 23..158С, Дои:10.1073 / pnas.23.3.158, ЧВК 1076889, PMID 16588141.
- de Groot, Sybren R .; Мазур, Питер (1984), Неравновесная термодинамика (2-е изд.), Нью-Йорк: Дувр.
- Duoandikoetxea, Хавьер (2001), Фурье-анализ, Американское математическое общество, ISBN 978-0-8218-2172-5.
- Дым, Х.; Маккин, Х. (1985), Ряды и интегралы Фурье, Академическая пресса, ISBN 978-0-12-226451-1.
- Эрдели, Артур, изд. (1954), Таблицы интегральных преобразований, 1, Макгроу-Хилл.
- Феллер, Уильям (1971), Введение в теорию вероятностей и ее приложения, II (2-е изд.), Нью-Йорк: Wiley, МИСТЕР 0270403.
- Фолланд, Джеральд (1989), Гармонический анализ в фазовом пространстве, Princeton University Press.
- Фурье, Дж. Б. Джозеф (1822), Теория аналитик де ла шалёр (на французском языке), Париж: Firmin Didot, père et fils, OCLC 2688081.
- Фурье, Дж. Б. Джозеф (1878) [1822], Аналитическая теория тепла, перевод Александра Фримена, The University Press (перевод с французского).
- Градштейн Израиль Соломонович; Рыжик Иосиф Моисеевич; Геронимус Юрий Вениаминович; Цейтлин Михаил Юльевич; Джеффри, Алан (2015), Цвиллинджер, Дэниел; Молл, Виктор Гюго (ред.), Таблица интегралов, серий и продуктов, переведено Scripta Technica, Inc. (8-е изд.), Академическая пресса, ISBN 978-0-12-384933-5.
- Графакос, Лукас (2004), Классический и современный анализ Фурье, Прентис-Холл, ISBN 978-0-13-035399-3.
- Графакос, Лукас; Тешл, Джеральд (2013), «О преобразованиях Фурье радиальных функций и распределений», J. Fourier Anal. Appl., 19: 167–179, arXiv:1112.5469, Дои:10.1007 / s00041-012-9242-5, S2CID 1280745.
- Greiner, W .; Рейнхардт, Дж. (1996), Квантование поля, Springer, ISBN 978-3-540-59179-5.
- Гельфанд, И.; Шилов, Г. (1964), Обобщенные функции, 1, Нью-Йорк: Академическая пресса (перевод с русского).
- Гельфанд, И.; Виленкин, Н. (1964), Обобщенные функции, 4, Нью-Йорк: Академическая пресса (перевод с русского).
- Хьюитт, Эдвин; Росс, Кеннет А. (1970), Абстрактный гармонический анализ, Die Grundlehren der Mathematischen Wissenschaften, Band 152, Vol. II: Структура и анализ компактных групп. Анализ на локально компактных абелевых группах, Springer, МИСТЕР 0262773.
- Хёрмандер, Л. (1976), Линейные дифференциальные операторы с частными производными, Vol. 1, Springer, ISBN 978-3-540-00662-6.
- Хоу, Роджер (1980), "О роли группы Гейзенберга в гармоническом анализе", Бюллетень Американского математического общества, 3 (2): 821–844, Дои:10.1090 / S0273-0979-1980-14825-9, МИСТЕР 0578375.
- Джеймс, Дж. Ф. (2011), Руководство по преобразованию Фурье для студентов (3-е изд.), Издательство Кембриджского университета, ISBN 978-0-521-17683-5.
- Иордания, Камилла (1883), Cours d'Analyse de l'École Polytechnique, Vol. II, Calcul Intégral: Intégrales définies et indéfinies (2-е изд.), Париж.
- Кайзер, Джеральд (1994), «Дружественный путеводитель по вейвлетам», Физика сегодня, 48 (7): 57–58, Bibcode:1995ФТ .... 48г..57К, Дои:10.1063/1.2808105, ISBN 978-0-8176-3711-8.
- Каммлер, Дэвид (2000), Первый курс анализа Фурье, Прентис Холл, ISBN 978-0-13-578782-3.
- Кацнельсон, Ицхак (1976), Введение в гармонический анализ, Дувр, ISBN 978-0-486-63331-2.
- Кириллов Александр; Гвишиани, Алексей Д. (1982) [1979], Теоремы и проблемы функционального анализа, Springer (перевод с русского).
- Кнапп, Энтони В. (2001), Теория представлений полупростых групп: обзор на примерах, Princeton University Press, ISBN 978-0-691-09089-4.
- Колмогоров Андрей Николаевич; Фомин Сергей Васильевич (1999) [1957], Элементы теории функций и функционального анализа, Дувр (перевод с русского).
- Ладо, Ф. (1971), «Численные преобразования Фурье в одном, двух и трех измерениях для расчетов жидкого состояния», Журнал вычислительной физики, 8 (3): 417–433, Bibcode:1971JCoPh ... 8..417L, Дои:10.1016/0021-9991(71)90021-0.
- Мюллер, Мейнард (2015), В двух словах о преобразовании Фурье. (PDF), В Основы обработки музыки, Раздел 2.1, страницы 40-56: Springer, Дои:10.1007/978-3-319-21945-5, ISBN 978-3-319-21944-8, S2CID 8691186CS1 maint: location (связь).
- Пейли, R.E.A.C.; Винер, Норберт (1934), Преобразования Фурье в комплексной области, Публикации коллоквиума Американского математического общества, Провиденс, Род-Айленд: Американское математическое общество.
- Пинский, Марк (2002), Введение в анализ Фурье и всплески, Брукс / Коул, ISBN 978-0-534-37660-4.
- Пуанкаре, Анри (1895), Теория аналитики пропаганды шалеров, Париж: Carré.
- Полянин, А.Д .; Манжиров, А. В. (1998), Справочник интегральных уравнений, Бока-Ратон: CRC Press, ISBN 978-0-8493-2876-3.
- Press, William H .; Флэннери, Брайан П .; Teukolsky, Saul A .; Веттерлинг, Уильям Т. (1992), Числовые рецепты на языке C: Искусство научных вычислений, второе издание (2-е изд.), Издательство Кембриджского университета.
- Рахман, Матюр (2011), Приложения преобразований Фурье к обобщенным функциям, WIT Press, ISBN 978-1-84564-564-9.
- Рудин, Вальтер (1987), Реальный и комплексный анализ (3-е изд.), Сингапур: McGraw Hill, ISBN 978-0-07-100276-9.
- Simonen, P .; Олкконен, Х. (1985), "Быстрый метод вычисления интегрального преобразования Фурье с помощью численного интегрирования Симпсона", Журнал биомедицинской инженерии, 7 (4): 337–340, Дои:10.1016/0141-5425(85)90067-6, PMID 4057997.
- Штейн, Элиас; Шакарчи, Рами (2003), Фурье-анализ: введение, Princeton University Press, ISBN 978-0-691-11384-5.
- Штейн, Элиас; Вайс, Гвидо (1971), Введение в анализ Фурье на евклидовых пространствах, Принстон, Нью-Джерси: Princeton University Press, ISBN 978-0-691-08078-9.
- Танежа, Х.С. (2008), «Глава 18: Интегралы Фурье и преобразования Фурье», Высшая инженерная математика, Vol. 2, Нью-Дели, Индия: I. K. International Pvt Ltd, ISBN 978-8189866563.
- Титчмарш, Э. (1986) [1948], Введение в теорию интегралов Фурье (2-е изд.) Оксфордского университета: Clarendon Press, ISBN 978-0-8284-0324-5.
- Вретблад, Андерс (2000), Фурье-анализ и его приложения, Тексты для выпускников по математике, 223, Нью-Йорк: Springer, ISBN 978-0-387-00836-3.
- Уиттакер, Э. Т.; Уотсон, Г.Н. (1927), Курс современного анализа (4-е изд.), Издательство Кембриджского университета.
- Виддер, Дэвид Вернон; Винер, Норберт (Август 1938 г.), «Замечания к классической формуле обращения для интеграла Лапласа», Бюллетень Американского математического общества, 44 (8): 573–575, Дои:10.1090 / с0002-9904-1938-06812-7.
- Винер, Норберт (1949), Экстраполяция, интерполяция и сглаживание стационарных временных рядов с помощью инженерных приложений, Кембридж, Массачусетс: Technology Press и John Wiley & Sons и Chapman & Hall.
- Уилсон, Р. Г. (1995), Ряды Фурье и методы оптического преобразования в современной оптике, Нью-Йорк: Wiley, ISBN 978-0-471-30357-2.
- Йосида, К. (1968), Функциональный анализ, Springer, ISBN 978-3-540-58654-8.

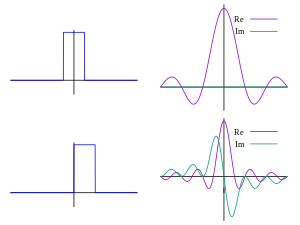






















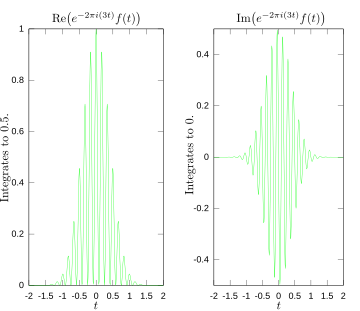
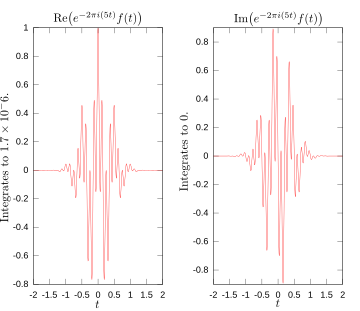
































![{ displaystyle psi _ {n} (x) = { frac { sqrt [{4}] {2}} { sqrt {n!}}} e ^ {- pi x ^ {2}} mathrm {He} _ {n} left (2x { sqrt { pi}} right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9121f54a3fdbb0eedecf2aef5a379bdfae414b7)




































































































































































































































































































































![{ displaystyle chi _ {[0,1]} (| mathbf {x} |) left (1- | mathbf {x} | ^ {2} right) ^ { delta}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1f3e6c1f52f0ee9366c40ee6f67c65f11dbd03a)























