WikiDer > Шестиугольная черепица Order-4
| Шестиугольная черепица Order-4 | |
|---|---|
 Модель диска Пуанкаре из гиперболическая плоскость | |
| Тип | Гиперболический правильный тайлинг |
| Конфигурация вершины | 64 |
| Символ Шлефли | {6,4} |
| Символ Wythoff | 4 | 6 2 |
| Диаграмма Кокстера | |
| Группа симметрии | [6,4], (*642) |
| Двойной | Квадратная черепица Order-6 |
| Характеристики | Вершинно-транзитивный, реберно-транзитивный, лицо переходный |
В геометрия, то гексагональная черепица порядка 4 это обычный облицовка гиперболическая плоскость. Она имеет Символ Шлефли из {6,4}.
Симметрия
Этот тайлинг представляет собой гиперболический калейдоскоп из 6 зеркал, определяющих фундаментальную область правильного шестиугольника. Эта симметрия орбифолдная запись называется * 222222 с 6 зеркальными пересечениями порядка 2. В Обозначение Кокстера можно представить в виде [6*, 4], сняв два из трех зеркал (проходящих через центр шестиугольника). Добавление биссектрисы через 2 вершины гексагональной фундаментальной области определяет трапецию. * 4422 симметрия. Добавление 3 пополам зеркала через вершины определяет * 443 симметрия. Добавление 3 пополам зеркала через край определяет * 3222 симметрия. Добавление всех 6 биссектрис приводит к полному * 642 симметрии.
 *222222 |  *443 |  *3222 |  *642 |
Равномерная окраска
Есть 7 различных равномерные раскраски для гексагональной черепицы порядка 4. Они похожи на 7 из равномерная окраска квадратной плитки, но исключить 2 случая с гирациональной симметрией второго порядка. Четыре из них имеют светоотражающие конструкции и Диаграммы Кокстера а трое из них - окраски.
| 1 цвет | 2 цвета | 3 и 2 цвета | 4, 3 и 2 цвета | ||||
|---|---|---|---|---|---|---|---|
| Униформа Окраска |  (1111) |  (1212) |  (1213) | 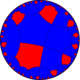 (1113) |  (1234) |  (1123) |  (1122) |
| Симметрия | [6,4] (*642) | [6,6] (*662) | [(6,6,3)] = [6,6,1+] (*663) | [1+,6,6,1+] (*3333) | |||
| Символ | {6,4} | г {6,6} = {6,4}1/2 | г (6,3,6) = г {6,6}1/2 | г {6,6}1/4 | |||
| Coxeter диаграмма | |||||||
Связанные многогранники и мозаика
Этот тайлинг топологически связан как часть последовательности регулярных мозаик с шестиугольник лица, начиная с шестиугольная черепица, с Символ Шлефли {6, n} и Диаграмма Кокстера ![]()
![]()
![]()
![]()
![]() , прогрессирующая до бесконечности.
, прогрессирующая до бесконечности.
| *п62 изменения симметрии правильных мозаик: {6,п} | ||||||||
|---|---|---|---|---|---|---|---|---|
| Сферический | Евклидово | Гиперболические мозаики | ||||||
 {6,2} |  {6,3} |  {6,4} |  {6,5} |  {6,6} |  {6,7} |  {6,8} | ... |  {6,∞} |
Эта мозаика также топологически связана как часть последовательности правильных многогранников и мозаик с четырьмя гранями на вершину, начиная с октаэдр, с Символ Шлефли {n, 4} и диаграмма Кокстера ![]()
![]()
![]()
![]()
![]() , при этом n стремится к бесконечности.
, при этом n стремится к бесконечности.
| *п42 мутации симметрии правильных мозаик: {п,4} | |||||||
|---|---|---|---|---|---|---|---|
| Сферический | Евклидово | Гиперболические мозаики | |||||
 |  |  |  |  |  |  | |
| 24 | 34 | 44 | 54 | 64 | 74 | 84 | ...∞4 |
| Изменение симметрии квазирегулярных мозаик: 6.n.6.n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия * 6n2 [n, 6] | Евклидово | Компактный гиперболический | Паракомпакт | Некомпактный | |||||||
| *632 [3,6] | *642 [4,6] | *652 [5,6] | *662 [6,6] | *762 [7,6] | *862 [8,6]... | *∞62 [∞,6] | [iπ / λ, 6] | ||||
| Квазирегулярный цифры конфигурация |  6.3.6.3 |  6.4.6.4 |  6.5.6.5 |  6.6.6.6 |  6.7.6.7 |  6.8.6.8 |  6.∞.6.∞ | 6.∞.6.∞ | |||
| Двойные цифры | |||||||||||
| Ромбический цифры конфигурация |  V6.3.6.3 |  V6.4.6.4 |  V6.5.6.5 |  V6.6.6.6 | V6.7.6.7 |  V6.8.6.8 |  V6.∞.6.∞ | ||||
| Равномерные тетрагексагональные мозаики | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия: [6,4], (*642) (с подсимметрией [6,6] (* 662), [(4,3,3)] (* 443), [∞, 3, ∞] (* 3222) индекса 2) (И [(∞, 3, ∞, 3)] (* 3232) подсимметрия индекса 4) | |||||||||||
= = = | = | = = = | = | = = = | = | ||||||
 |  |  |  |  |  |  | |||||
| {6,4} | т {6,4} | г {6,4} | т {4,6} | {4,6} | rr {6,4} | tr {6,4} | |||||
| Униформа двойников | |||||||||||
 |  |  |  |  |  |  | |||||
| V64 | V4.12.12 | V (4,6)2 | V6.8.8 | V46 | V4.4.4.6 | V4.8.12 | |||||
| Чередования | |||||||||||
| [1+,6,4] (*443) | [6+,4] (6*2) | [6,1+,4] (*3222) | [6,4+] (4*3) | [6,4,1+] (*662) | [(6,4,2+)] (2*32) | [6,4]+ (642) | |||||
= | = | = | = | = | = | ||||||
 |  |  |  |  |  |  | |||||
| ч {6,4} | с {6,4} | ч. {6,4} | с {4,6} | ч {4,6} | чрр {6,4} | sr {6,4} | |||||
| Равномерные шестиугольные мозаики | ||||||
|---|---|---|---|---|---|---|
| Симметрия: [6,6], (*662) | ||||||
= | = | = | = | = | = | = |
 |  |  |  |  |  |  |
| {6,6} = ч {4,6} | т {6,6} = h2{4,6} | г {6,6} {6,4} | т {6,6} = h2{4,6} | {6,6} = ч {4,6} | рр {6,6} г {6,4} | тр {6,6} т {6,4} |
| Униформа двойников | ||||||
 |  |  |  |  |  |  |
| V66 | V6.12.12 | V6.6.6.6 | V6.12.12 | V66 | V4.6.4.6 | V4.12.12 |
| Чередования | ||||||
| [1+,6,6] (*663) | [6+,6] (6*3) | [6,1+,6] (*3232) | [6,6+] (6*3) | [6,6,1+] (*663) | [(6,6,2+)] (2*33) | [6,6]+ (662) |
 |  |  |  |  | ||
| ч {6,6} | с {6,6} | ч. {6,6} | с {6,6} | ч {6,6} | чрр {6,6} | sr {6,6} |
| Подобные мозаики H2 в симметрии * 3232 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Coxeter диаграммы | ||||||||
| Вершина фигура | 66 | (3.4.3.4)2 | 3.4.6.6.4 | 6.4.6.4 | ||||
| Изображение |  |  |  |  | ||||
| Двойной |  |  | ||||||
| Равномерные мозаики в симметрии * 3222 | ||||
|---|---|---|---|---|
 |  |  |  | |
 |  |  | ||
 |  |  | ||
Смотрите также
| Викискладе есть медиафайлы по теме Шестиугольная черепица Order-4. |
- Квадратная плитка
- Замощения правильных многоугольников
- Список однородных плоских мозаик
- Список правильных многогранников
Рекомендации
- Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штрасс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
- «Глава 10: Обычные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе. Dover Publications. 1999 г. ISBN 0-486-40919-8. LCCN 99035678.

