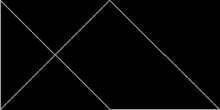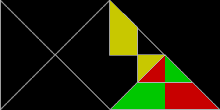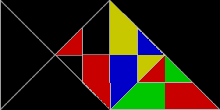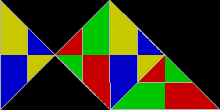
WikiDer > Реп-плитка
в геометрия из мозаика, а реплика или же рептилия это форма, которая может быть рассеченный на уменьшенные копии той же формы. Термин был придуман как каламбур на животных рептилии к математик-любитель Соломон В. Голомб и популяризируется Мартин Гарднер в его "Математические игры"в майском номере журнала 1963 г. Scientific American.[1] В 2012 году обобщение реп-тайлов под названием наборы плитки самоклейки был представлен Ли Саллоус в Математический журнал.[2]
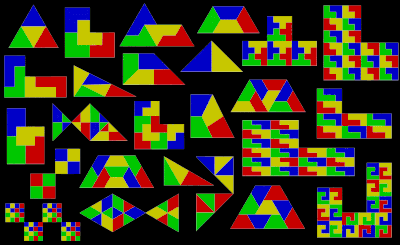
Терминология
Репликация помечена как реп-п если вскрытие использует п копии. Такая форма обязательно образует прототип для мозаики плоскости во многих случаях апериодическая мозаика. Диссекция повторной плитки с использованием различных размеров исходной формы называется неправильной повторной плиткой или непрактичной. Если при вскрытии используется п копии, форма считается неповрежденнойп. Если все эти суб-тайлы имеют разные размеры, то мозаика дополнительно описывается как идеальная. Форма, которая реп-п или неп тривиально также является неисправным (кн − k + п) для любого k > 1, заменив самую маленькую плитку в реп-п рассечение п плитки еще меньшего размера. Порядок фигур, независимо от того, используются ли плитки повторения или плитки повторения, - это наименьшее возможное количество плиток, которого будет достаточно.[3]
Примеры

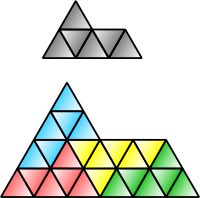
Каждый квадрат, прямоугольник, параллелограмм, ромб, или же треугольник Реп-4. В сфинкс шестиугольник (показано выше) - это rep-4 и rep-9, и это один из немногих известных самовоспроизводящиеся пятиугольники. В Остров Госпер Реп-7. В Коха снежинка is irp-7: шесть маленьких снежинок одинакового размера вместе с другой снежинкой, площадь которой в три раза больше, чем у меньших, могут объединиться в одну большую снежинку.
А прямоугольный треугольник с длинами сторон в соотношении 1: 2 - реп-5, а ее рассечение реп-5 составляет основу апериодической вертушка черепица. К Теорема Пифагора, то гипотенуза, или наклонная сторона треугольника rep-5, имеет длину √5.
Международный стандарт ISO 216 определяет размеры листов бумаги с помощью √2, в котором длинная сторона прямоугольного листа бумаги является квадратный корень из двух раз короткую сторону бумаги. Прямоугольники в этой форме - rep-2. Прямоугольник (или параллелограмм) повторяется.п если это соотношение сторон является √п: 1. An равнобедренный прямоугольный треугольник тоже реп-2.
Репликация и симметрия
Некоторые реплики, например квадрат и равносторонний треугольник, находятся симметричный и остаются идентичными, когда отражение в зеркале. Другие, как сфинкс, находятся асимметричный и существовать в две различные формы связаны зеркальным отражением. Рассечение сфинкса и некоторых других асимметричных реплитов требует использования как исходной формы, так и ее зеркального отображения.
Реп-плитки и полиформы
Некоторые реп-плитки основаны на полиформы подобно полиалмазы и полимино, или формы, созданные путем укладки равносторонние треугольники и квадраты от края до края.
Квадраты
Если полимино исправимо, то есть может выложить плитку прямоугольник, то это также будет повторный тайл, потому что прямоугольник будет иметь целочисленное отношение длины стороны и, таким образом, будет замощен квадрат. Это можно увидеть в октимино, которые созданы из восьми квадратов. Две копии некоторых октимино выложат квадрат; поэтому эти октимино также представляют собой реп-16 реп-плиток.

Четыре копии некоторых нономино и ничтожества выложит квадрат, поэтому эти полиформы также реп-36 реп-плиток.
Равносторонние треугольники
Аналогично, если полиалмаз плитки равностороннего треугольника, это также будет повторная плитка.
Правые треугольники
А прямоугольный треугольник представляет собой треугольник, содержащий один прямой угол в 90 °. Две особые формы прямоугольного треугольника привлекли внимание исследователей изобразительного искусства: треугольник 45 ° -90 ° -45 ° и треугольник 30 ° -60 ° -90 °.
45 ° -90 ° -45 ° треугольники
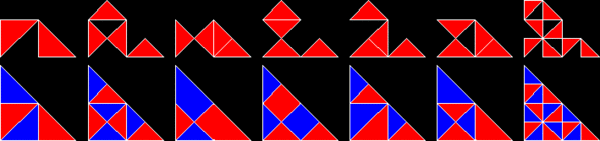
Полиформы на основе равнобедренный прямоугольные треугольники, со сторонами в соотношении 1: 1:√2, известны как полиаболос. Бесконечное количество из них - реплики. Действительно, самый простой из всех повторных плиток - это один равнобедренный прямоугольный треугольник. Это rep-2, если разделить его одной линией, разделяющей прямой угол пополам. гипотенуза. Реп-2 Реп-плитки также реп-2п а треугольники rep-4,8,16 + дают дополнительные плитки репликации. Их можно найти, отбрасывая половину субкопий и переставляя оставшиеся, пока они не будут зеркально-симметричный в прямоугольном треугольнике. Другими словами, две копии образуют прямоугольный треугольник. Одна из этих новых повторяющихся плиток напоминает рыбу, образованную из трех равносторонние треугольники.
30 ° -60 ° -90 ° треугольники
Полиформы на основе прямоугольных треугольников 30 ° -60 ° -90 °, со сторонами в соотношении 1:√3 : 2, известны как полидрафтеры. Некоторые идентичны полимино и полиалмазы, другие различны.[4]
Множественные и вариативные репликации
Многие из обычных репсовых плиток являются репрезентативными.п2 для всех положительных целых значенийп. В частности, это верно для трех трапеции включая треугольник, образованный из трех равносторонних треугольников, для трех параллельных оси шестиугольников (L-тромино, L-тетромино и P-пентамино) и шестиугольника сфинкса.[5] Кроме того, многие повторные плитки, особенно с более высоким показателем.п, можно выложить плиткой разными способами. Например, L-тетрамино rep-9 имеет по крайней мере четырнадцать различных реплиций. Шестиугольник реп-9 сфинкс тоже можно облицовывать по-разному.
Реплики с бесконечными сторонами
Наиболее знакомые повторяющиеся плитки - это многоугольники с конечным числом сторон, но некоторые формы с бесконечным числом сторон также могут быть повторными плитками. Например, терагонический треугольник, или рогатый треугольник, есть реп-4. Это также пример фрактальная реплика.
Пятиугольная реплика
Треугольные и четырехугольные (четырехсторонние) повторяющиеся плитки распространены, но пятиугольные повторяющиеся плитки встречаются редко. Долгое время сфинкс широко считалось, что это единственный известный пример, но Немецкий/Новая Зеландия математик Карл Шерер и американский математик Джордж Сичерман нашли больше примеров, включая двойную пирамиду и удлиненную версию сфинкса. Эти пятиугольные реплики изображены на Математическая магия страницы, курируемые американским математиком Эрих Фридман.[6] Однако сфинкс и его расширенные версии - единственные известные пятиугольники, которые можно повторно выложить равными копиями. Страницы рептилий.
Реп-тайлы и фракталы
Реплицировать плитки как фракталы
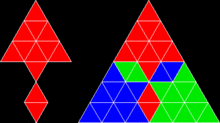
Rep-плитки можно использовать для создания фракталы, или фигуры, которые самоподобный в меньших и меньших масштабах. Фрактал повторной плитки формируется путем разделения повторной плитки, удаления одной или нескольких копий разделенной формы и последующего продолжения рекурсивно. Например, Ковер Серпинского формируется таким образом из повторного разбиения квадрата на 27 меньших квадратов, а Треугольник Серпинского формируется путем повторения мозаики равностороннего треугольника на четыре меньших треугольника. Когда одна суб-копия выбрасывается, rep-4 L-триомино можно использовать для создания четырех фракталов, два из которых идентичны, за исключением ориентация.
Фракталы как реп-тайлы
Потому что фракталы самоподобны в меньших и меньших масштабах, многие из них могут быть разложены на копии самих себя, как повторяющийся тайл. Однако если фрактал имеет пустой интерьер, это разложение не может привести к замощению всей плоскости. Например, Треугольник Серпинского реп-3, выложенный тремя собственными копиями, а Ковер Серпинского реп-8, выложенный восемью копиями самого себя, но повторение этих разложений не образует мозаику. С другой стороны, кривая дракона это кривая заполнения пространства с непустым салоном; это rep-4, и он действительно образует плитку. Точно так же Остров Госпер представляет собой rep-7, образованный из заполняющей пространство кривой Госпера, и снова образует мозаику.
По построению любой фрактал, определяемый система повторяющихся функций из n карт с одинаковым соотношением это rep-n.
Бесконечная мозаика
Среди правильных многоугольников только треугольник и квадрат можно разрезать на более мелкие копии одинакового размера. Однако регулярный шестиугольник можно разрезать на шесть равносторонних треугольников, каждый из которых можно разрезать на правильный шестиугольник и еще три равносторонних треугольника. Это основа для бесконечного черепица шестиугольника с шестиугольниками. Следовательно, шестиугольник - это безрезультатно или безумие-бесконечность бесполезна.
Смотрите также
Примечания
Рекомендации
- Гарднер, М. (2001), «Rep-Tiles», Колоссальная книга математики: классические головоломки, парадоксы и задачи, Нью-Йорк: W. W. Norton, стр. 46–58.
- Гарднер, М. (1991), «Глава 19: Реплики, репликации фигур на плоскости», Неожиданное зависание и другие математические отклонения, Чикаго, Иллинойс: Издательство Чикагского университета, стр. 222–233.
- Лэнгфорд, К. Д. (1940), "Использование геометрической головоломки", Математический вестник, 24 (260): 209–211, Дои:10.2307/3605717
- Niţică, Виорел (2003), «Повторный визит Rep-tile», МАССА selecta, Провиденс, Род-Айленд: Американское математическое общество, стр. 205–217, МИСТЕР 2027179
- Саллоус, Ли (2012), «О наборах самозакладывающейся плитки», Математический журнал, 85 (5): 323–333, Дои:10.4169 / math.mag.85.5.323, МИСТЕР 3007213
- Шерер, Карл (1987), Загадочное путешествие к рептилиям и родственным животным
- Уэллс, Д. (1991), Словарь любопытной и интересной геометрии Penguin, Лондон: Penguin, стр. 213–214.
внешняя ссылка
Реп-плитки
| Викискладе есть медиафайлы по теме Реп-плитки. |
- Математический центр Сфинкс Альбом: http://mat Mathematicscentre.com/taskcentre/sphinx.htm
- Кларк, А. Л. Рептилии. http://www.recmath.com/PolyPages/PolyPages/Reptiles.htm.
- Вайсштейн, Эрик В. "Реп-Плитка". MathWorld.
- http://www.uwgb.edu/dutchs/symmetry/reptile1.htm (1999)
- IFStile - программа для поиска реп-тайлов: https://ifstile.com