WikiDer > Буддхаброт

А Буддхаброт повторяется до 20000 раз.

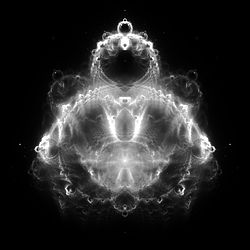
В Буддхаброт - распределение вероятностей по траекториям точек, покидающих Фрактал Мандельброта. Его название отражает его парейдолический сходство с классическими изображениями Гаутама Будда, сидящий в позе медитации со знаком на лбу (тикка), традиционный хохолок (ушниша) и локон волос.

Открытие

В Буддхаброт технику рендеринга открыла Мелинда Грин,^[1] который позже описал это в 1993 г. Usenet пост в sci.fractals.^[2]

Предыдущие исследователи были очень близки к открытию точной техники Буддхаброт. В 1988 году Линас Вепстас передал похожие изображения.^[3] к Клифф Пиковер для включения в готовящуюся к печати книгу Пиковера Компьютеры, Узоры, Хаос и Красота. Это привело непосредственно к открытию Подборщики стеблей. Однако эти исследователи не отфильтровали неизбегающие траектории, необходимые для создания призрачных форм, напоминающих индуистское искусство. Обратный фильтр «Anti-Buddhabrot» создает изображения, похожие на отсутствие фильтрации.

Грин первым назвал этот узор Ганешем, поскольку индийский коллега «сразу же узнал в нем бога».Ганеша«с головой слона».^[2] Название Буддхаброт был придуман позже Лори Гарди.^[4]

Метод рендеринга

Математически множество Мандельброта состоит из набор очков ${ displaystyle c}$ в комплексная плоскость для чего итеративно определенный последовательность

$${ displaystyle z_ {n + 1} = {z_ {n}} ^ {2} + c}$$

делает нет как правило бесконечность в качестве ${ displaystyle n}$ уходит в бесконечность для ${ displaystyle z_ {0} = 0}$.

Небулаброт в котором красный, зеленый и синий каналы были повторены 5000, 500 и 50 раз соответственно.

В Буддхаброт изображение можно создать, сначала создав 2-размерный множество прямоугольников, каждая из которых соответствует конечному пикселю изображения. Каждая коробка ${ displaystyle (я, j)}$ за ${ Displaystyle я = 1, ldots, м}$ и ${ displaystyle j = 1, ldots, n}$ имеет размер в комплексных координатах ${ displaystyle Delta x}$ и ${ displaystyle Delta y}$, куда ${ displaystyle Delta x = w / m}$ и ${ displaystyle Delta y = h / n}$ для изображения шириной ${ displaystyle w}$ и высота ${ displaystyle h}$. Для каждого ящика соответствующий счетчик обнуляется. Затем случайная выборка ${ displaystyle c}$ точки повторяются через функцию Мандельброта. Для точек, которые делать уйти в течение выбранного максимального числа итераций, и поэтому нет в наборе Мандельброта счетчик для каждого окна, введенного во время перехода на бесконечность, увеличивается на 1. Другими словами, для каждой последовательности, соответствующей ${ displaystyle c}$ что убегает, за каждую точку ${ displaystyle z_ {n}}$ во время побега ящик, ${ displaystyle ({ text {Re}} (z_ {n}), { text {Im}} (z_ {n}))}$ находится внутри увеличивается на 1. Точки, которые не исчезают в течение максимального числа итераций (и считаются находящимися в наборе Мандельброта), отбрасываются. После большого количества ${ displaystyle c}$ значения были повторены, оттенки серого затем оттенки выбираются на основе распределения значений, записанных в массиве. В результате на графике плотности выделяются области, где ${ displaystyle z_ {n}}$ ценности тратят больше всего времени на пути к бесконечности.

Анти-буддхаброт

Буддхаброт по мере увеличения максимального числа итераций

Нюансы

Рендеринг Буддхаброт изображения обычно требуют больших вычислительных ресурсов, чем стандартные методы рендеринга Мандельброта. Частично это связано с тем, что для создания четкого изображения требуется повторение большего количества случайных точек, чем пикселей в изображении. Рендеринг сильно увеличенных областей требует даже большего количества вычислений, чем для стандартных изображений Мандельброта, в которых данный пиксель может быть вычислен напрямую, независимо от уровня масштабирования. И наоборот, на пиксель в увеличенной области изображения Buddhabrot могут влиять начальные точки из областей, далеко выходящих за пределы визуализируемой. Не прибегая к более сложным вероятностным методам,^[5] рендеринг увеличенных частей Буддхаброт состоит из простой обрезки большого полноразмерного рендеринга.

Максимальное количество выбранных итераций влияет на изображение - более высокие значения дают более разреженный и детализированный вид, поскольку несколько точек проходят через большое количество пикселей, прежде чем уйти, в результате чего их пути становятся более заметными. Если бы использовался более низкий максимум, эти точки не ускользнули бы вовремя и будут считаться не ускользающими вообще. Выбранное количество выборок также влияет на изображение, поскольку большее количество выборок не только снижает шум изображения, но и может уменьшить видимость медленно движущихся точек и небольших аттракторов, которые могут отображаться как видимые полосы при рендеринге с меньшим количеством выборок. . Некоторые из этих полос видны на изображении 1000000 итераций ниже.

Позже Грин понял, что это естественный способ создания цветных изображений Буддхаброт, сделав три таких оттенки серого изображения, различающиеся только максимальным количеством используемых итераций, и объединение их в одноцветное изображение с использованием того же метода, который использовали астрономы для создания ложный цвет изображения туманностей и других небесных объектов. Например, можно назначить изображение с максимальной итерацией 2000 для красного канала, изображение с максимальной итерацией 200 для зеленого канала и изображение с максимальной итерацией 20 для синего канала изображения в Цветовое пространство RGB. Некоторые маркируют изображения Буддхаброт с помощью этой техники. Небулаброты.

Максимальное количество итераций: 20

Максимальное количество итераций: 100

Максимальное количество итераций: 1000

Максимальное количество итераций: 20000

Максимальное количество итераций: 1000000

Отношение к логистической карте

Буддхаброт и его логистическая карта.

Анимация, изображающая Буддхаброт и его логистическую карту.

Отношения между Набор Мандельброта как определено итерацией ${ displaystyle z ^ {2} + c}$, а логистическая карта ${ Displaystyle лямбда х (1-х)}$ хорошо известен. Эти два связаны квадратичным преобразованием:

$${ displaystyle { begin {align} c_ {r} & = { frac { lambda (2- lambda)} {4}} c_ {i} & = 0 z_ {r} & = - { frac { lambda (2x-1)} {2}} z_ {i} & = 0 end {align}}}$$

Традиционный способ проиллюстрировать эту взаимосвязь - согласовать логистическую карту и набор Мандельброта через взаимосвязь между ${ displaystyle c_ {r}}$ и ${ displaystyle lambda}$, используя общую ось x и другую ось y, показывающую одномерную взаимосвязь.

Мелинда Грин обнаружила «случайно», что парадигма анти-буддхаброта полностью интегрирует логистическую карту. Оба основаны на отслеживании путей от неоткрывающихся точек, повторяются от (случайной) начальной точки, а итерационные функции связаны преобразованием, приведенным выше. Тогда легко увидеть, что Антибуддхаброт для ${ displaystyle z ^ {2} + c}$, прокладывая пути с ${ displaystyle c = ({ text {random}}, 0)}$ и ${ displaystyle z_ {0} = (0,0)}$, просто создает логистическую карту в самолете ${ Displaystyle {c_ {r}, z_ {r} }}$, при использовании данного преобразования. Для визуализации мы используем ${ displaystyle z_ {0} = ({ text {random}}, 0)}$. На логистической карте все ${ displaystyle z_ {r0}}$ в конечном итоге создать тот же путь.

Поскольку и набор Мандельброта, и логистическая карта являются неотъемлемой частью Anti-Buddhabrot, теперь мы можем показать трехмерную взаимосвязь между ними, используя трехмерные оси.${ Displaystyle {c_ {r}, c_ {i}, z_ {r} }}$. В анимации показан классический антибуддаброт с ${ displaystyle c = ({ text {random}}, { text {random}})}$ и ${ displaystyle z_ {0} = (0,0)}$, это двумерное множество Мандельброта на плоскости${ displaystyle {c_ {r}, c_ {i} }}$, а также Anti-Buddhabrot с ${ displaystyle c = ({ text {random}}, 0)}$ и ${ displaystyle z_ {0} = (0,0)}$, это двухмерная логистическая карта на плоскости ${ displaystyle {c_ {r}, z_ {r} }}$. Вращаем самолет ${ displaystyle {c_ {i}, z_ {r} }}$ вокруг ${ displaystyle c_ {r}}$ось, первое показание ${ displaystyle {c_ {r}, c_ {i} }}$, затем поверните на 90 °, чтобы показать ${ Displaystyle {c_ {r}, z_ {r} }}$, затем повернув еще на 90 °, чтобы показать ${ displaystyle {c_ {r}, - c_ {i} }}$. Мы могли бы повернуть еще на 180 °, но это дает те же изображения, отраженные вокруг ${ displaystyle c_ {r}}$-ось.

Логистическая карта Anti-Buddhabrot на самом деле является разновидностью классической Anti-Buddhabrot, расположенной в плоскости ${ Displaystyle {c_ {r}, z_ {r} }}$ (или же ${ displaystyle c_ {i} = 0}$) 3D ${ Displaystyle {c_ {r}, c_ {i}, z_ {r} }}$, перпендикулярно плоскости ${ displaystyle {c_ {r}, c_ {i} }}$. Мы подчеркиваем это, показывая кратко при повороте на 90 ° только спроецированную плоскость. ${ displaystyle c_ {i} = 0}$, не `` возмущенная '' проекциями плоскостей с ненулевым ${ displaystyle c_ {i}}$.

Рекомендации

внешняя ссылка

Викискладе есть медиафайлы по теме Буддхаброт.

• Лобо, Альберт. «Познакомьтесь с техникой Буддхаброт». Молекулярная плотность. Архивировано из оригинал на 2018-09-03. Получено 2011-11-21.
• Матолог. «Темная сторона множества Мандельброта». YouTube.